[C++] 백준 2660. 회장뽑기 - 플로이드 워셜 알고리즘

알고리즘

목록 보기

14/20

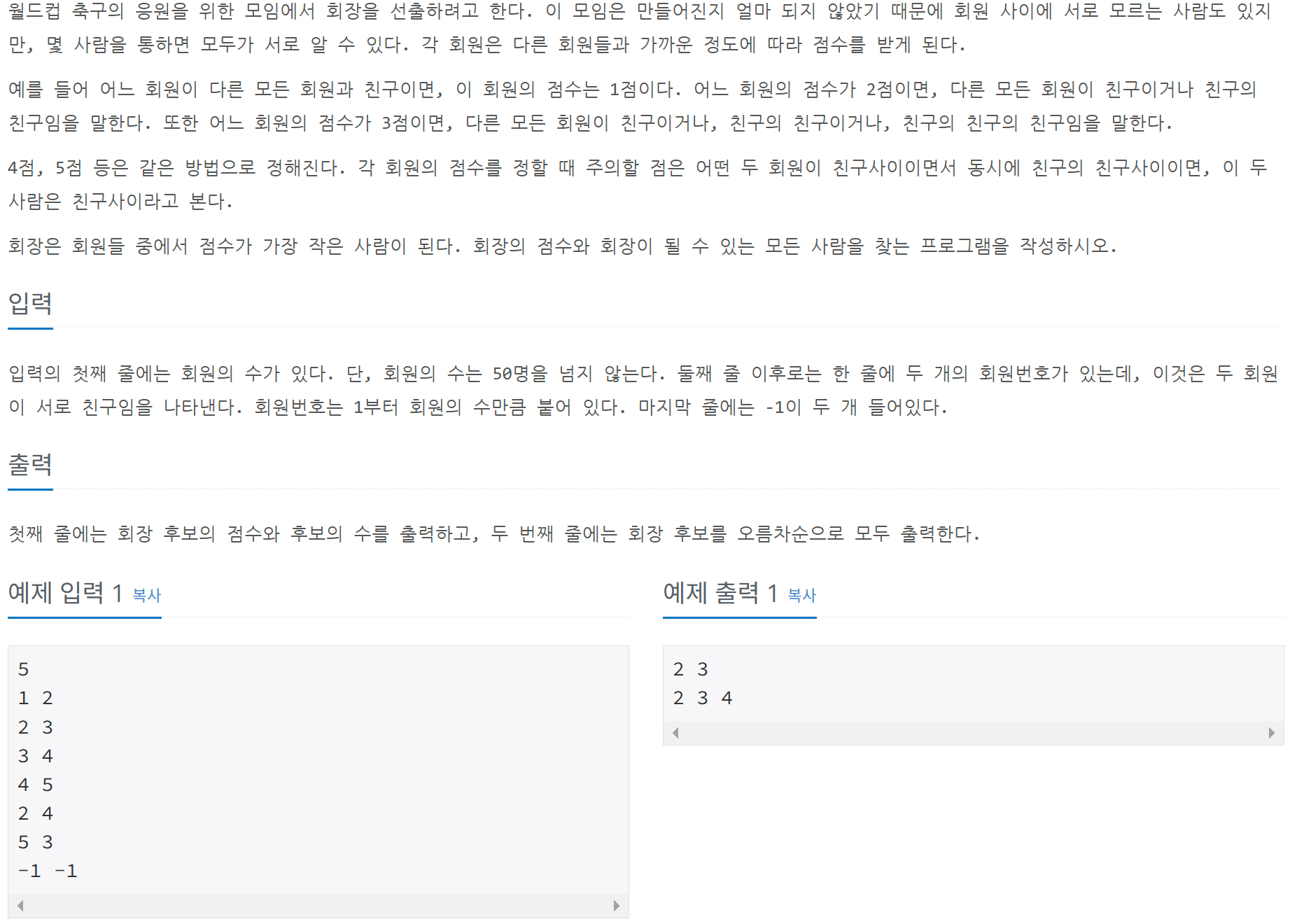
문제

풀이 - BFS

골드는 그래프를 좋아하는구나 하면서 dfs를 해볼까 하고
이리저리 디버깅 해보다가 bfs를 써야된다는 걸 알았다.
블로거들의 풀이와 나의 기억을 더듬어서 어찌저찌 해결을 했다.
BFS로 최대 깊이를 구해서 최소 점수를 가진 인덱스를 출력하면 된다.

코드 - BFS

#include <iostream>
#include <algorithm>
#include <vector>
#include <queue>

using namespace std;

int n;
int a, b;
vector<int> v[51];
vector<int> ans;

int bfs(int i) {
	int visit[51] = { 0, };
	visit[i] = 1;

	queue<pair<int, int>> q;
	q.push({ i, 0 });

	int maxi = 0;
	while (!q.empty()) {
		int now = q.front().first;
		int step = q.front().second;
		maxi = max(maxi, step);
		q.pop();

		for (int j = 0; j < v[now].size(); j++) {
			int next = v[now][j];
			if (visit[next]) continue;
			visit[next] = 1;
			q.push({ next, step + 1 });
		}
	}
	return maxi;
}

int main() {
	cin >> n;
	while (1) {
		cin >> a >> b;
		if (a == -1 && b == -1) break;
		v[a].push_back(b);
		v[b].push_back(a);
	}

	int mini = 1e9;
	for (int i = 1; i <= n; i++) {
		int score = bfs(i);
		if (score < mini) {
			mini = score;
			ans.clear();
			ans.push_back(i);
		}
		else if (score == mini) {
			ans.push_back(i);
		}
	}

	cout << mini << " " << ans.size() << "\n";
	for (int it : ans) {
		cout << it << " ";
	}

	return 0;
}

BFS 풀이를 찾다보니 여기저기서 자꾸 보이는 게 있었는데
아우 모른척 할래다가 지금 하지 언제 하냐 싶어서
어쩔 수 없이 공부를 시작했다.

플로이드-워셜(Floyd-Warshall) 알고리즘

보니까 학부 때 배웠던 건데 그 때 더 잘 정리해둘걸, 하는 생각이 들었다.
지금이라도 정리하고 있으니 다행이지 응

플로이드-워셜 알고리즘은 그래프에서 가능한 모든 노드 쌍에 대해 최단 거리를 구하는 알고리즘이다.

비슷한 알고리즘으로 하나의 노드로부터 나머지 모든 노드로의 최단 거리를 구하는 다익스트라 알고리즘이 있는데,
플로이드-워셜 알고리즘은 모든 노드 쌍에 대해 최단 거리를 구하고, 음의 가중치를 가지는 그래프에서도 쓸 수 있다는 것이 특징이다.

예제

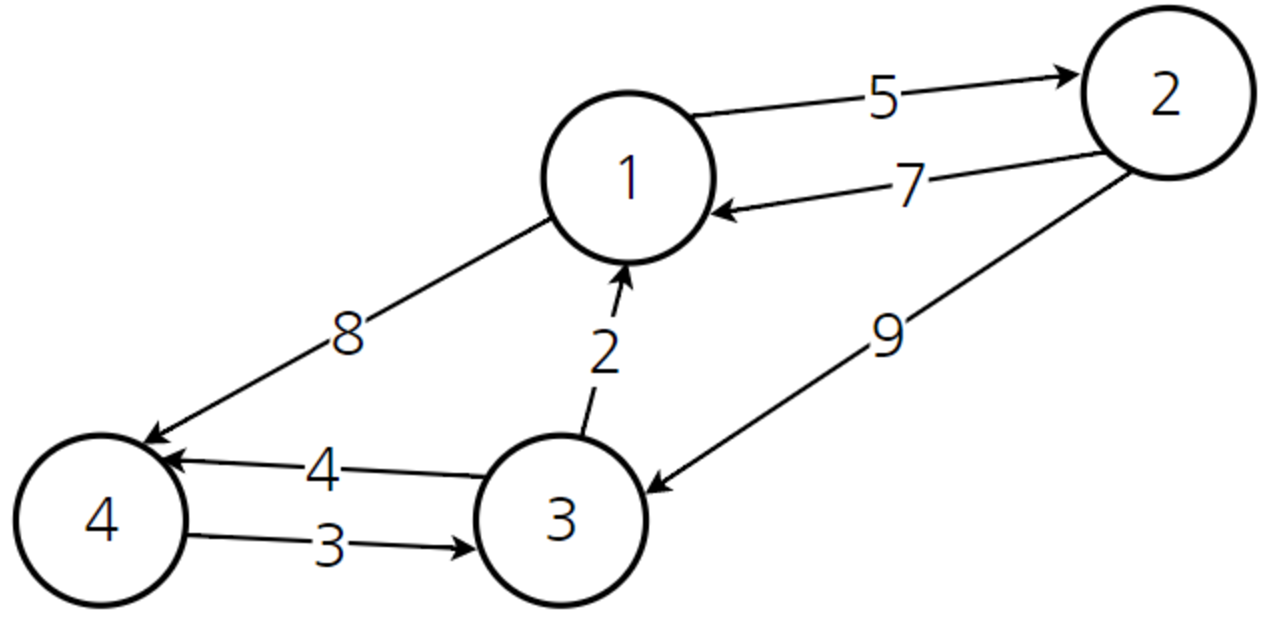
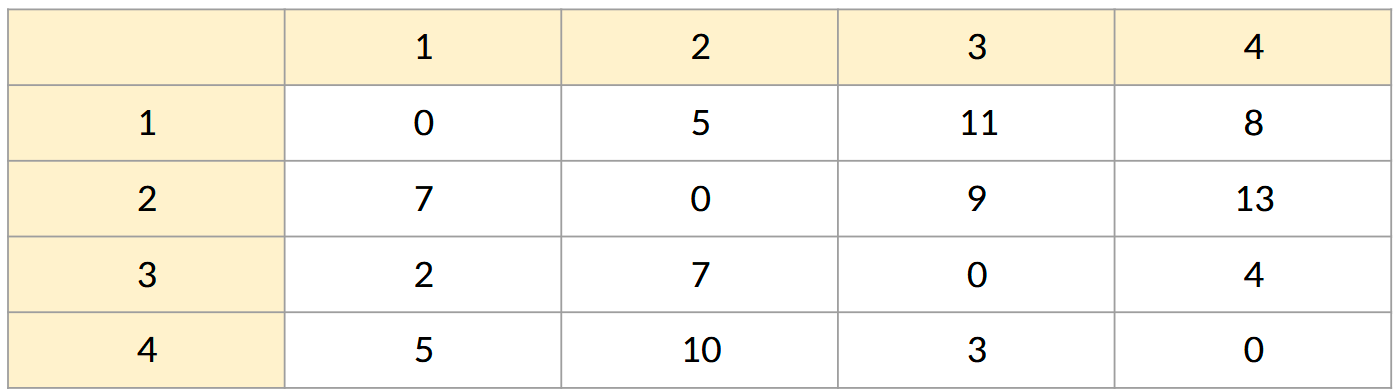
이런 그래프가 있다고 할 때, 각 노드로부터 다른 노드로의 거리를 아래와 같이 표현할 수 있다.

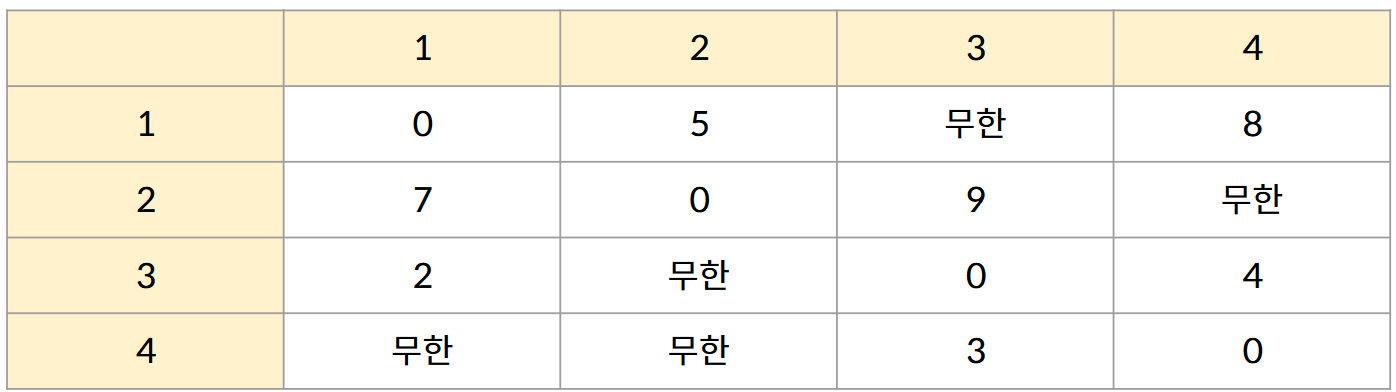
이 이차원 배열을 어떠한 기준에 맞게 갱신해가는 될텐데,
이 기준이 바로 '거쳐가는 점'이다.

1번을 거치는 경우

이미 1번이 포함되어 다시 계산할 필요가 없는 1행, 1열,
그리고 각자 자신으로 돌아오는 대각선 배열을 제외하고 갱신하면 된다.

예를 들어 3에서 2번으로 가는 거리는 무한이었지만
3에서 1로 갔다가 1에서 2로 가는 거리는 2 + 5 = 7으로 갱신되는 식이다.

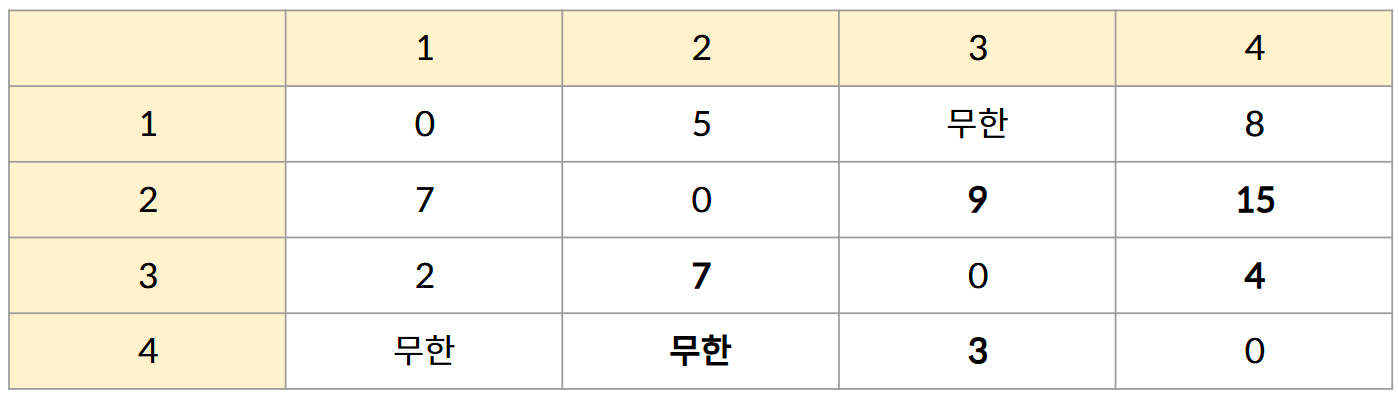
2~4번을 거치는 경우

같은 방식으로 모든 노드의 거리를 갱신하면 아래와 같이 각 노드들에서 다른 노드들로의 최소 거리를 구할 수 있게 된다.

풀이 - 플로이드 워셜

먼저 노드 간 거리를 구할 dist 배열을 선언한다.
자기 자신과의 거리는 0이므로 continue, 그 외는 무한으로 초기화해준 뒤 서로 친구라고 하는 사람들은 값으로 1을 넣어준다.

플로이드 워셜 알고리즘으로 각 노드 간 거리값을 갱신하고,
회장감을 계산해 출력해주면 된다.

코드 - 플로이드 워셜

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

#define INF 1e9;

int n;
int a, b;
int dist[51][51] = { 0, };
vector<int> ans;

int main() {
	cin >> n;

	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			if (i == j) continue;
			dist[i][j] = INF;
		}
	}

	while (1) {
		cin >> a >> b;
		if (a == b) break;
		dist[a][b] = 1;
		dist[b][a] = 1;
	}

	for (int k = 1; k <= n; k++) {
		for (int i = 1; i <= n; i++) {
			for (int j = 1; j <= n; j++) {
				if (dist[i][j] > dist[i][k] + dist[k][j]) {
					dist[i][j] = dist[i][k] + dist[k][j];
				}
			}
		}
	}

	int score = INF;
	for (int i = 1; i <= n; i++) {
		int maxi = 0;
		for (int j = 1; j <= n; j++) {
			maxi = max(maxi, dist[i][j]);
		}
		if (maxi < score) {
			score = maxi;
			ans.clear();
			ans.push_back(i);
		}
		else if (maxi == score) {
			ans.push_back(i);
		}
	}

	cout << score << " " << ans.size() << "\n";
	for (int it : ans) {
		cout << it << " ";
	}

	return 0;
}