[AI] AI 모델링 (Regularization, Logistic Regression, Regression)

1. 레귤러라이제이션 (Regularization)

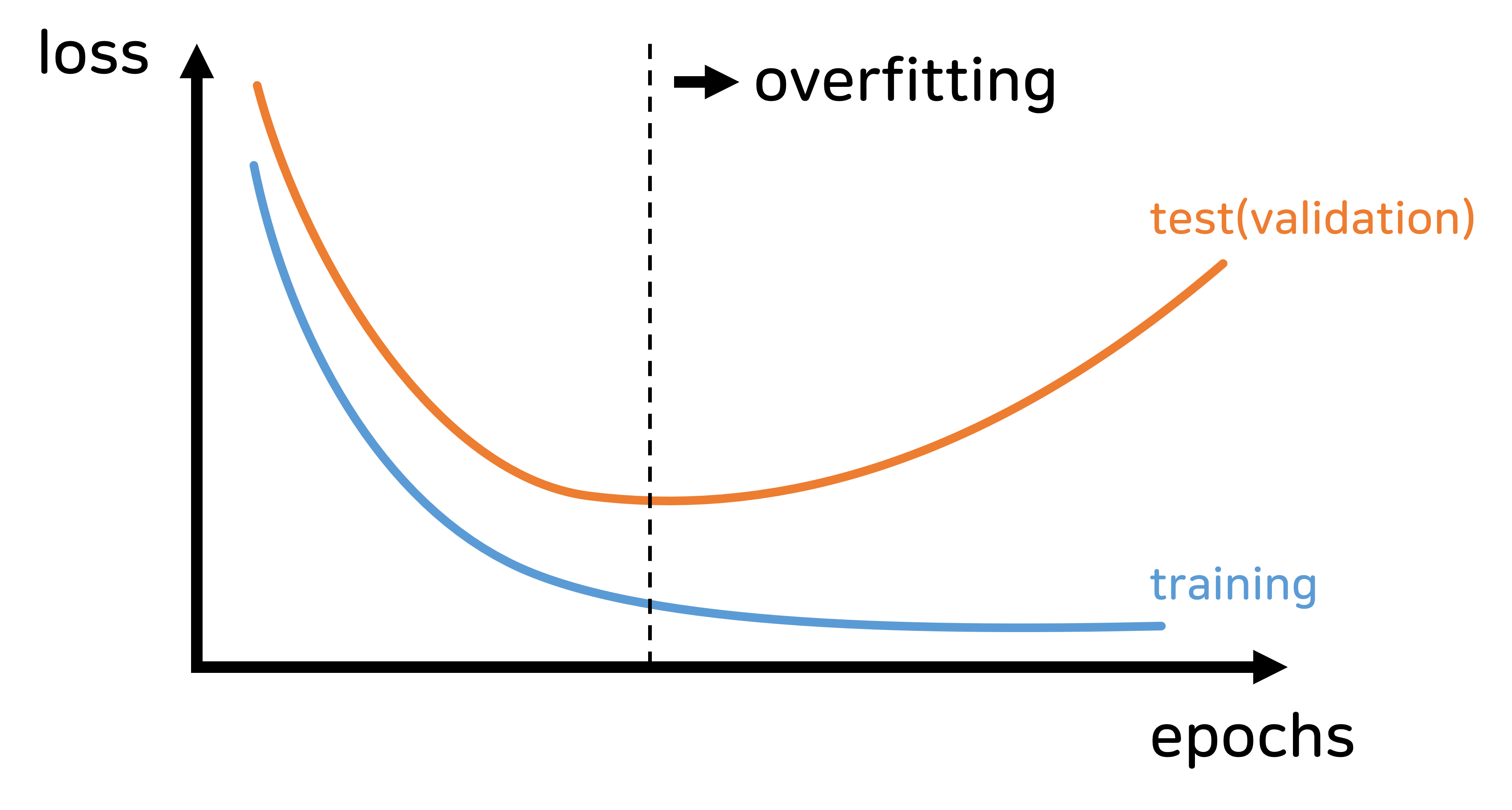
• 레귤러라이제이션은 모델이 학습 데이터에 너무 과적합(overfitting)되는 것을 방지하기 위해 사용하는 기법입니다.

  • 레귤러라이제이션을 통해 모델이 더욱 일반화된(generalized) 성능을 발휘하도록 하는 것이 목적입니다.

• L1 정규화 (Lasso Regression): 비용 함수에 가중치 절댓값( $||W||_1$)을 추가하여 모델의 복잡성을 줄입니다.

  • 일부 가중치를 0으로 만들기 때문에 특성 선택(feature selection)에 유용합니다.

• L2 정규화 (Ridge Regression): 비용 함수에 가중치 제곱합( $||W||_2^2$)을 추가합니다.

  • 가중치를 너무 크게 만드는 것을 방지하여 모델의 복잡성을 줄입니다.

• Elastic Net: L1과 L2 정규화를 함께 사용하는 방법으로, 두 방법의 장점을 결합합니다.

2. 로지스틱 회귀 (Logistic Regression)

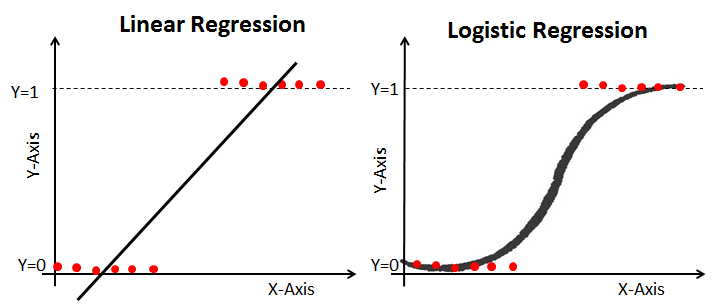
• 로지스틱 회귀는 종속 변수가 이산형(대개 이진형)인 경우 사용되는 통계 모델입니다.

  • 예를 들어, 이메일이 스팸인지 아닌지, 환자가 특정 질병을 가졌는지 여부를 예측할 때 사용됩니다.

• 비용 함수: 로지스틱 회귀의 비용 함수는 로그 손실(log loss)을 사용합니다.

  • $J(\theta) = -\frac{1}{m} \sum_{i=1}^{m} y^{(i)} \log(h_\theta(x^{(i)})) + (1 - y^{(i)}) \log(1 - h_\theta(x^{(i)}))$

    • $J(\theta)$: 이것은 비용 함수입니다.

      • 이 함수는 모델의 파라미터 $\theta$에 대한 함수이며, 이 값이 낮을수록 모델의 예측이 실제 레이블에 더 가깝다는 것을 의미합니다.

    • $m$: 데이터 포인트의 총 개수입니다.

    • $i$: 데이터 포인트의 인덱스를 나타냅니다. 따라서 $(i = 1)$부터 $m$까지 존재합니다.

    • $y^{(i)}$: $i$번째 데이터 포인트의 실제 레이블입니다. 이는 0 또는 1일 수 있습니다.

    • $h_\theta(x^{(i)})$: $(i)$번째 데이터 포인트에 대해 모델이 예측한 확률입니다.

      • 이를 로지스틱 회귀에서는 시그모이드 함수로 구할 수 있습니다.

        • $h_\theta(x) = \frac{1}{1 + e^{-\theta^T x}}$

시그모이드 함수

• 시그모이드 함수: 로지스틱 회귀의 결과는 선형 회귀와 달리 시그모이드 함수를 통해 0과 1 사이의 확률로 변환됩니다.

  • $\sigma(x) = \frac{1}{1 + e^{-x}}$

    • $\sigma(x)$: x에 대한 시그모이드 함수의 출력

    • $e$: 자연로그의 밑(약 2.718)

    • $x$: 입력값

1. 출력 범위: 시그모이드 함수는 입력값을 0과 1 사이의 값으로 변환합니다.

   • 예를 들어 로지스틱 회귀에서 클래스 1일 확률을 표현하는 데 유용합니다.

2. S-형 곡선: 시그모이드 함수의 그래프는 S-모양을 하고 있어 이를 S-형 함수라고도 부릅니다.

   • 이 곡선은 입력값이 클수록(양의 무한대에 가까울수록) 1에 가까워지고, 입력값이 매우 작을수록(음의 무한대에 가까울수록) 0에 가까워집니다.

   • 중간값인 0일 때 함수의 출력은 0.5입니다.

3. 미분 가능성: 시그모이드 함수는 미분 가능하며, 이는 기계 학습 알고리즘에서 중요합니다.

   • 시그모이드 함수의 도함수는 간단하게 계산될 수 있으며, 다음과 같습니다: $\sigma'(x) = \sigma(x) (1 - \sigma(x))$

4. 모노톤 증가: 시그모이드 함수는 입력값이 증가하면 출력값도 증가하는 단조 증가 함수입니다.

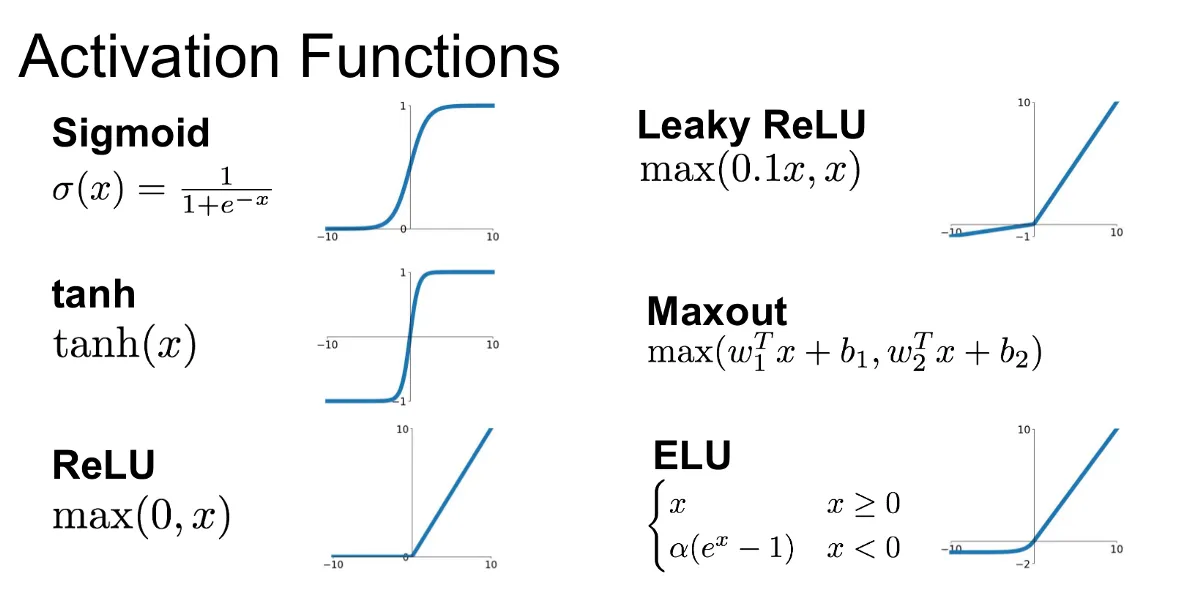
5. 활성화 함수로의 사용: 신경망에서 시그모이드 함수는 뉴런의 출력값을 계산하는 활성화 함수로 자주 사용됩니다.

   • 이를 통해 뉴런의 출력값을 비선형 변환하여 모델이 복잡한 패턴을 학습할 수 있게 합니다.

• 잠재적인 단점

  • 밴싱 문제: 입력값의 절대값이 클 경우(양의 무한대 또는 음의 무한대에 가까운 경우), 그래디언트가 매우 작아집니다.

    • 이로 인해 역전파 동안 그래디언트 소실 문제(vanishing gradient problem)가 발생할 수 있습니다. 이 문제는 심층 신경망의 학습을 어렵게 합니다.

  • 출력 중심: 출력 값이 0.5를 중심으로 대칭적으로 분포되어 있어, 출력값이 음수 값으로 치우쳐진 경우 조정이 필요할 수 있습니다.

  • 이러한 이유로 최근에는 ReLU(Rectified Linear Unit)와 같은 다른 활성화 함수(ReLU, Leaky ReLU 등)도 많이 사용되고 있습니다.

    • 하지만 시그모이드 함수는 여전히 그 직관성과 특성 덕분에 중요하게 여겨지는 함수 중 하나입니다.

3. 리그레션 (Regression)

• 리그레션은 하나 이상의 독립 변수와 종속 변수 간의 관계를 모델링하는 기법입니다.

  • 종속 변수가 연속형일 때 주로 사용됩니다.

<독립변수 & 종속변수 복습>

• 독립변수
  • 독립변수란 어떤 실험에서 실험자가 직접 변경하는 변수를 의미합니다.
  • 수학에서는 대부분의 경우 어떤 식의 독립변수를 $x$로 표시합니다.
    • 예제: 용돈을 벌기 위해 집안일을 돕는다고 가정합시다. 집안일 한 개당 용돈 $3를 받습니다. 독립변수는 무엇일까요?
      • 독립변수는 해야하는 집안일의 양입니다. 왜냐하면, 이 변수는 스스로 바꿀 수 있는 값이기 때문입니다.
• 종속변수
  • 종속변수란, 독립변수의 값이 변함에 따라 달라지는 수량을 나타내는 변수입니다.
  • 등식에서는 대부분의 경우 $y$를 종속변수로 표현합니다.
    • 예제: 위와 같은 가정을 해 봅시다. 용돈을 벌기 위해 집안일을 돕는다고 가정합시다. 집안일 한 개당 용돈 $3를 받습니다. 종속변수는 무엇일까요?
      • 종속변수는 집안일을 해서 버는 용돈입니다. 왜냐하면, 벌 수 있는 용돈의 양은 해야하는 집안일의 양에 달려있기 때문입니다.

• 선형 회귀 (Linear Regression): 가장 기본적인 회귀 기법으로, 독립 변수와 종속 변수 간의 선형 관계를 모델링합니다.

  • 예를 들어, 단순 선형 회귀는 다음과 같은 형태를 가집니다.

    • $y = mx + b$

• 다중 선형 회귀 (Multiple Linear Regression): 다수의 독립 변수를 포함하는 선형 회귀 모델입니다.

  • $y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \ldots + \beta_n x_n$

• 다항 회귀 (Polynomial Regression): 독립 변수의 다항식을 사용하여 선형이 아닌 관계를 모델링합니다.

  • $y = \beta_0 + \beta_1 x + \beta_2 x^2 + \ldots + \beta_n x^n$

• 이 두 개념이 데이터에서 패턴을 찾아내는 데 중요한 역할을 합니다.

  • 각자의 용도와 상황에 맞추어 적절한 모델을 선택하는 것이 중요합니다.