벡터란?
-
벡터(vector)는 수학개념으로 크기와 방향을 갖는 물리량을 의미한다.
-
일반적으로 벡터는 시점과 끝점을 연결하는 화살표로 표시할 수 있다.
-
-
벡터와 상대되는 물리양으로 크기만 갖는 양을 스칼라(scalar)라고 하며, 질량, 시간, 면적 등과 같은 양이다.
-
벡터량은 속도, 가속도, 힘, 응력과 같은 크기와 방향을 갖는 양이다.
-
예를 들면, 벡터공간(3차원 실수공간)에서 임의 벡터
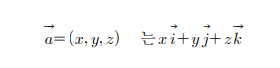
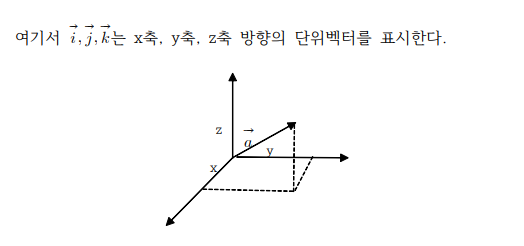
-
단위벡터
-
단위벡터는 크기가 1이고 방향을 갖는 벡터를 말한다.
-
벡터란 단위벡터를 벡터의 크기만큼 배수한 것으로 볼 수 있다.
-
단위벡터는 벡터를 벡터의 크기로 나누는 벡터 정규화 공식을 통해 구할 수 있다.


오일러각 & 쿼터니언
오일러각
-
오일러 각은 강체의 방향을 3차원 공간 좌표계의 회전으로 이해하는 것이다.
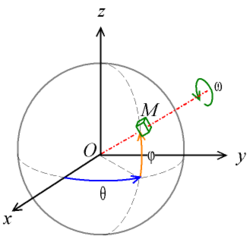
- 회전된 좌표계의 각도는 다음과 같이 정의된다.
-
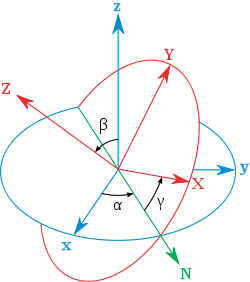
주어진 3차원 공간 좌표계를 (x, y, z)라고 하고, 이를 회전시킨 좌표계를 (X,Y,Z)라고 하면, 강체의 방향은 다음의 세 각도로 표시될 수 있다.
-
α(또는 ψ): z-축(파란색)을 회전축으로 하여 회전된 x-y 좌표축의 각도 -
β(또는 θ): 회전된 x-축(즉, N-축, 녹색)을 회전축으로 하여 회전된 z-y 좌표축의 각도 -
γ(또는 φ): 위에서 회전된 z-축(즉, Z축, 빨간색)을 회전축으로 하여 회전된 x-y 좌표축의 각도
-
-
위와 같이 하여 강체의 방향은 세 개의 각도로 표시될 수 있다.
-
로봇 제어와 같은 기기 제어에서는 ψ, θ, φ의 표현이 자주 쓰인다.
-
오일러 각은 강체의 자세를 좌표축의 회전으로 표현하는 여러 방법 가운데 하나로 회전축의 순서에 따라 Z-X-Z 좌표라고도 불린다.
-
오일러 각 이외에 강체의 자세를 표현하는 방법으로는 좌표계 (X, Y, Z)에 대해 X축 회전을 롤, Y축 회전을 피치, Z축 회전을 요라고 표기하는 X-Y-Z 좌표인 요, 피치, 롤 방식이 있다.
-
-
오일러 각의 범위는 α와 γ의 경우 이상적인 상황에서 2π 라디안까지이며, β의 경우 -π/2에서 π/2까지가 된다. β 범위가 제한적인 것을 짐벌 락(영어: gimbal lock) 이라 하는데, 이는 앞서 회전한 두 축의 영향으로 세 번째 회전의 가동 범위가 줄어들기 때문이다. 아폴로 11호의 경우 짐벌 락 때문에 자세 제어에 어려움이 있었다.
쿼터니언
-
사원수 (Quaternion)
-
3차원 그래픽에서 회전을 표현할 때, 행렬 대신 사용하는 수학적 개념으로 4개의 값으로 이루어진 복소수(Complex Number) 체계이다.
-
사원수는 행렬에 비해 연산 속도가 빠르고, 차지하는 메모리의 양도 적으며, 결과의 질에 있어 오류가 날 확률이 적다.
-
사원수는 4차원 복소수 공간(Complex Space)의 벡터로서 다음과 같이 나타낸다.
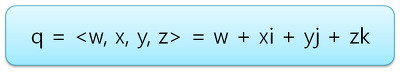
- 여기서
s는 q의 w 성분에 해당하는 스칼라(Scalar) 값이고,v는 q의 x, y, z 성분에 해당하는 벡터(Vector) 부분
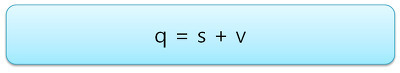
- 여기서
-
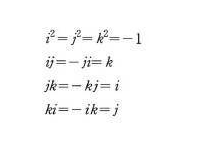
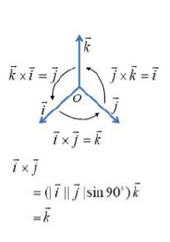
-
사원수는 곱셈의 교환법칙이 성립하지 않는다.
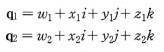
- 위와 같은 두 사원수
q1,q2가 있을 때, 두 사원수의 곱q1q2는 다음과 같다.
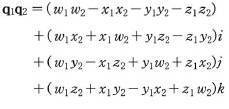
-
사원수를 스칼라, 벡터 형태로 표기
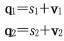
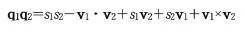
- 위와 같은 두 사원수
- 사원수는 켤레(Conjugate)를 갖는다.

- 사원수의 역수

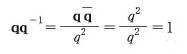
-
단위 쿼터니언
q = [1, (0, 0, 0)]
-
사원수의 보간
- 보간(interpolation)
- 처음과 끝의 값을 가지고 중간에 잇는 값을 계산해 내는 것이다.
- 물체의 애니메이션을 수행할 때, 보간을 통해 계산된 키프레임 사이의 중간 방향을 생성한다.
- 가장 간단한 보간은 선형보간(linear interpolation)으로 두 개의 값을 점으로 생각하고 두 개의 점을 이어주는 직선의 방정식으로부터 값을 얻어내는 방법이다.
-
두 사원수
q1,q2에 대해, 선형 보간된 사원수q(t)는 다음과 같다.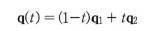
-
이런 사원수는 정규화 해줘야 한다. 이 함수 q(t)는 q1과 q2사이의 호를 따라간다.
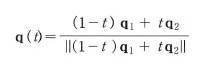
-
그림은 2차원 단면이나, 실제로는 4차원 단위 초구면 상의 경로를 따라간다.
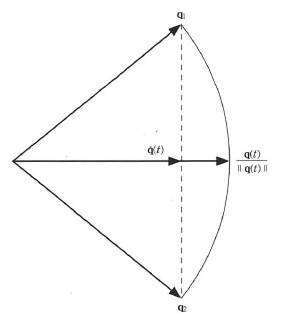
이러한 선형 보간은 간단하고, 효과적이나 호를 일정한 비율로 추적하지 않는다는 문제가 있다.
- 여기에서 구면 선형보간(spherical linear interpolation : slerp)이 나타났다.
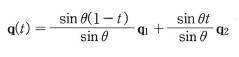
- 보간(interpolation)
