📌문제
N×M크기의 배열로 표현되는 미로가 있다.
미로에서 1은 이동할 수 있는 칸을 나타내고, 0은 이동할 수 없는 칸을 나타낸다. 이러한 미로가 주어졌을 때, (1, 1)에서 출발하여 (N, M)의 위치로 이동할 때 지나야 하는 최소의 칸 수를 구하는 프로그램을 작성하시오. 한 칸에서 다른 칸으로 이동할 때, 서로 인접한 칸으로만 이동할 수 있다.
위의 예에서는 15칸을 지나야 (N, M)의 위치로 이동할 수 있다. 칸을 셀 때에는 시작 위치와 도착 위치도 포함한다.
입력
첫째 줄에 두 정수 N, M(2 ≤ N, M ≤ 100)이 주어진다. 다음 N개의 줄에는 M개의 정수로 미로가 주어진다. 각각의 수들은 붙어서 입력으로 주어진다.
출력
첫째 줄에 지나야 하는 최소의 칸 수를 출력한다. 항상 도착위치로 이동할 수 있는 경우만 입력으로 주어진다.
예제 입력1
4 6
101111
101010
101011
111011예제 출력1
15예제 입력2
4 6
110110
110110
111111
111101예제 출력2
9예제 입력3
2 25
1011101110111011101110111
1110111011101110111011101예제 출력3
38예제 입력4
7 7
1011111
1110001
1000001
1000001
1000001
1000001
1111111예제 출력4
13💡Idea
문제를 보고, BFS를 사용하여 해결했던 백준 토마토 문제가 떠올랐습니다.
토마토 문제에서 상자 안 특정 위치에만 존재하는 토마토를 모두 탐색했던 것처럼, 미로에서 이동할 수 있는 칸인 1이 존재하는 칸들을 탐색하면 문제를 해결할 수 있을 것으로 생각했습니다.
단 반드시 모든 칸을 탐색할 필요는 없고, (N, M)의 위치에 도달하면 탐색을 멈추면 됩니다.
1이 적혀진 칸을 각각 노드로, 미로를 각 인접한 1이 적힌 칸들 사이가 edge로 연결된 그래프로, (1, 1)이 적힌 칸을 시작 노드로 생각해봅시다!
그래프를 원하는 노드가 나올 때까지 BFS로 탐색하는 과정으로 생각하면 문제를 해결할 수 있습니다.
💻코드
from collections import deque
import sys
input = sys.stdin.readline
N, M = map(int, input().split())
arr = [[0] * (M + 2)]+([[0]+(list(map(int, list(input().strip()))))+([0])
for _ in range(N)])+[[0] * (M + 2)]
deq = deque([(1, 1, 1)])
visited = [[0, 0]]
edges = [[1, 0], [0, 1], [-1, 0], [0, -1]] # 위, 아래, 양 옆의 칸 확인
while deq:
x, y, d = deq.popleft()
if x == N and y == M: # (N, M) 칸에 도달하면 출력 후 종료
print(d)
break
for i in range(4):
nx = x + edges[i][0]
ny = y + edges[i][1]
if arr[nx][ny] == 1 and [nx, ny] not in visited:
deq.append((nx, ny, d+1))
visited.append([nx, ny])📝코드 설명
변수
N,M: 미로(배열)의 크기arr: 미로를 담은 리스트deq: BFS에서 사용할 큐,[2차원 배열의 index, 시작 칸으로부터의 거리]로 값이 추가된다.visited: 방문한 노드들을 담은 리스트edges: 인접한 노드들을 계산하기 위한 4개의 좌표
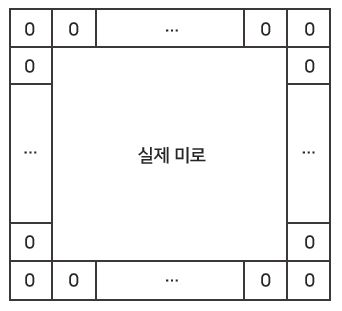
우선 입력된 N과 M에 맞게 arr 에 입력되는 미로를 저장하였습니다.
이 때 후에 유효한 좌표인지를 확인하는 과정을 생략하기 위하여 실제 미로를 0의 값으로 한 번 감싸줍니다.
(감싸지 않고, 0-base로 코드를 작성한 경우 0<=nx<=N와 0<=ny<=M의 범위 내에 있는지 확인이 필요)
이후, 큐를 사용하여 BFS로 노드들을 탐색합니다.
원하는 (N, M) 칸에 도달하면, 시작 노드로부터 떨어져있는 거리 출력 후 종료합니다.