🔍그래프 탐색
그래프를 탐색하는 방법에는 두 가지가 있습니다.
하나는 너비를 우선으로 탐색하는 방법(breadth-first search), 다른 하나는 깊이를 우선으로 탐색하는 방법(deapth-first search)입니다.
📌여기서 그래프 탐색이란?
- 그래프를 탐색한다는 것은 하나의 정점에서 시작하여, 차례대로 모든 정점들을 한 번씩 방문하는 것을 뜻합니다.
그래프를 탐색하는 순서에 따라서 BFS와 DFS를 구분할 수 있고, 두 알고리즘에 사용되는 자료구조와 구현 방식이 다릅니다. 한 번 자세히 알아봅시다👩🏫
BFS(Breadth-first serach, 너비 우선 탐색)
🤔BFS란?
-
BFS는 루트 노드(혹은 다른 임의의 노드)에서 시작하여 인접한 노드들을 우선으로 탐색하는 방법입니다.
즉, 현재 노드와 가까이 있는 노드들을 우선으로 탐색하고 멀리 있는 노드들은 나중에 탐색하는 것이죠! -
시작 노드로부터 깊이가 1인 노드들을 먼저 탐색하고, 그 다음에 깊이가 2인 노드, 깊이가 3인 노드 등의 순서로 노드를 탐색하는 것으로도 이해할 수 있습니다.
-
두 노드 사이의 최단 경로 혹은 임의의 경로를 찾고 싶을 때 BFS를 많이 사용합니다.
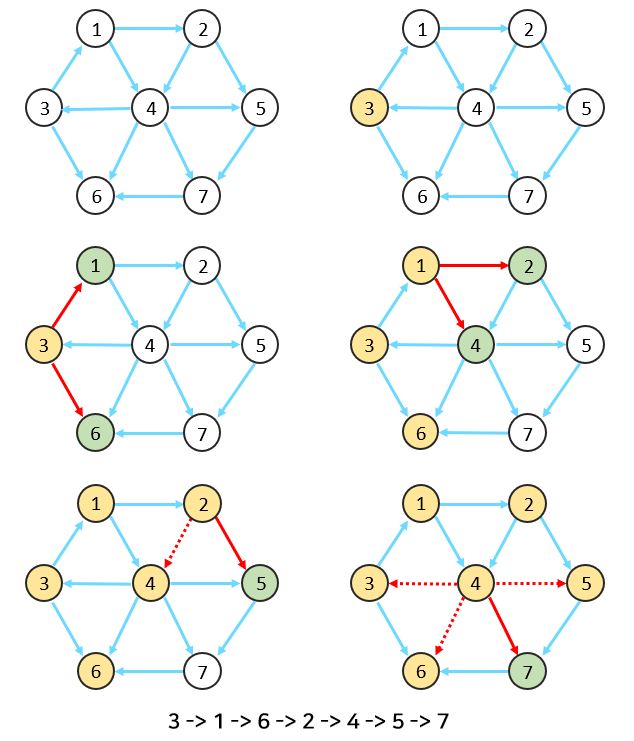
👇BFS로 그래프 탐색 예시 (시작 노드가 3인 경우)
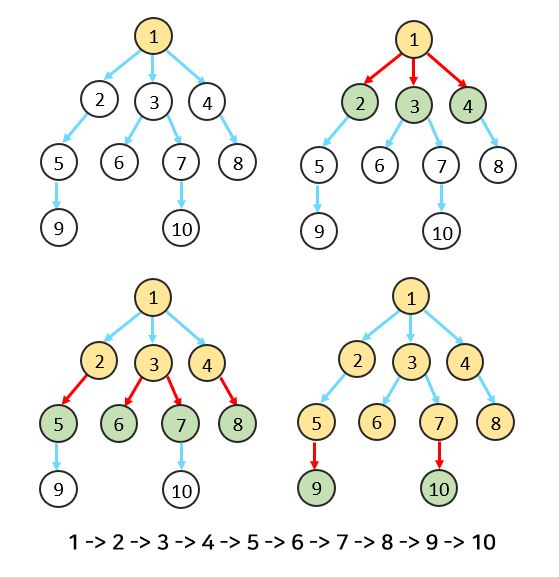
👇BFS로 트리 탐색 예시
- 트리와 같은 그래프로 확인해보면, 용어 그대로 깊이가 아닌 옆으로 탐색하는 것을 더 쉽게 확인할 수 있습니다.
BFS의 구현
- BFS는 큐로 구현할 수 있습니다.
- 시작 노드를 큐에 넣으면서 시작합니다.
- 큐에서 노드를 하나 뺀 뒤, 해당 노드와 연결되어 있는 노드들을 모두 큐에 넣습니다.
- 이 때, 한 번 큐에 들어간 노드들은 다시 재방문하지 않도록 따로 체크해줍니다.
- 큐에 아무 노드도 들어가있지 않을 때까지 2번과 3번을 반복합니다.
💡 큐는 FIFO이기 때문에, 먼저 큐에 들어간 깊이가 얕은 노드들이 먼저 탐색이 됩니다. 따라서, BFS는 큐로 구현이 가능한 것입니다!
💻BFS 코드
from collections import deque
def bfs(edge, n, v):
deq = deque([v]) # 시작 노드를 큐에 삽입
visited = [v] # 시작 노드를 방문 체트 리스트에 삽입
while deq: # 큐에 노드가 없으면 종료
current = deq.popleft() # 큐에서 노드 꺼내기
print(current, end=' ')
for i in range(1, n+1): # 노드들이 1번부터 n번까지 있다고 가정
if edge[current][i] == 1 and i not in visited:
deq.append(i)
visited.append(i)
변수
edge: 노드들의 연결 여부를 담고 있는 이차원 배열로, 1의 값을 가지면 해당 노드들이 연결되어 있음n: 노드의 개수v: 시작 노드deq: 노드들을 담을 큐를 표현하기 위해collections의deque사용visited: 노드들의 재방문을 방지하기 위한 방문했던 노드들을 담아놓는 리스트current: 현재 큐에서 꺼낸 노드
DFS(Deapth-first serach, 깊이 우선 탐색)
🤔DFS란?
-
DFS는 루트 노드(혹은 임의의 노드)에서 시작하여 다른 브런치로 넘어가기 전 해당 브런치의 모든 노드를 완벽히 탐색한 뒤, 다른 브런치로 넘어가 탐색하는 방법입니다.
즉, 현재 노드로부터 한 방향으로 끝까지 탐색하고 더 이상 갈 수 없게 되면 가장 가까운 갈림길로 되돌아와 다시 그 방향으로 탐색하는 것이죠! -
BFS에 비해 간단하나, 단순 검색 속도 자체는 BFS에 비해 느립니다
-
모든 노드들을 탐색해야 하는 경우에 많이 사용합니다.
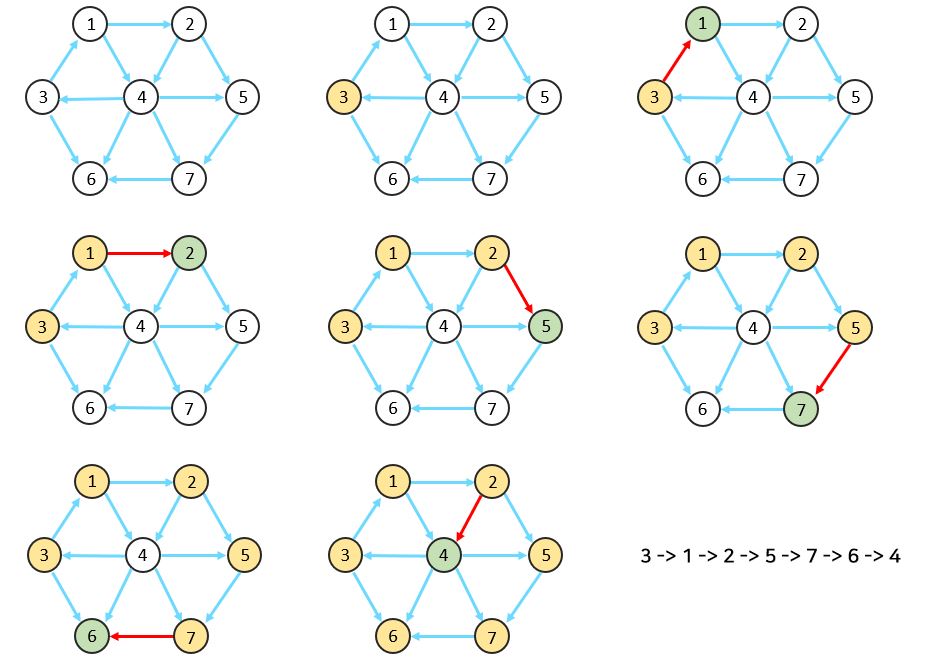
👇DFS로 그래프 탐색 예시 (시작 노드가 3인 경우)
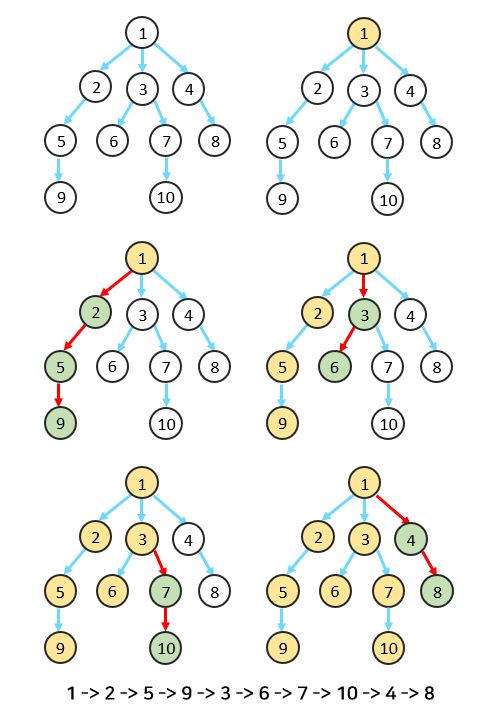
👇DFS로 트리 탐색 예시
- 트리와 같은 그래프로 확인해보면, 용어 그대로 옆으로가 아닌, 깊이 탐색하는 것을 더 쉽게 확인할 수 있습니다.
DFS의 구현
- DFS는 스택이나 재귀 함수를 통해서 구현할 수 있습니다.
스택으로 DFS 구현
- 시작 노드를 스택에 넣으면서 시작합니다.
- 스택에서 노드를 하나 뺀 뒤, 해당 노드가 처음 방문하는 노드라면 연결된 모든 노드들을 스택에 넣어줍니다.
- 이 때, 한 번 스택에서
pop되어 해당 노드와 연결되어 있는 노드들을 탐색한 노드는 다시 재방문하지 않도록 따로 체크해줍니다. - 스택에 아무 노드도 들어가있지 않을 때까지 2번과 3번을 반복합니다.
재귀로 DFS 구현
- DFS의 경우, 하나의 노드와 연결되어 있는 노드들을 끝까지 탐색해나가기 때문에 재귀로 쉽게 표현이 가능합니다.
- 현재 노드와 연결되어 있는 노드들을 확인합니다.
- 방문한 적이 없는 노드라면 해당 노드와 연결되어 있는 다른 노드들에 대해서 다시 dfs 탐색을 하도록 합니다.
- 이 때, 한 번 자신과 연결되어 있는 노드들을 탐색했던 노드는 재방문하지 않도록 따로 체크해줍니다.
- 연결되어 있는 노드들을 전부 방문했다면, 재귀가 종료되고 탐색이 종료됩니다.
💻DFS 코드
스택으로 구현한 DFS
def dfs_use_stack(edge, n, v):
deq = deque([v]) # 스택에 첫 번째 노드 삽입
visited = []
while deq: # 스택에 아무 노드가 없을 때까지 반복
current = deq.pop() # 스택에서 노드를 꺼냄
if current not in visited: # 아직 방문하지 않은 노드라면 연결된 노드 스택 삽입
print(current, end=' ')
visited.append(current)
for i in range(n, 0, -1): # 1
if edge[current][i] == 1:
deq.append(i)
#1 : 숫자가 작은 노드 우선으로 탐색하기 위해 큰 숫자의 노드부터 스택에 삽입하였습니다. 스택은 나중에 넣은 것이 먼저 나오기 때문에, 숫자가 작은 노드가 가장 마지막에 들어가면 큰 숫자의 노드보다 작은 숫자의 노드가 먼저 스택에서 나오면서 탐색됩니다.
재귀로 구현한 DFS
def dfs_use_recursive(edge, visited, n, v):
print(v, end=' ')
for i in range(1, n+1):
if edge[v][i] == 1 and i not in visited: # 아직 탐색되지 않은 노드라면 재귀적으로 dfs 탐색
visited.append(i)
dfs_use_recursive(edge, visited, n, i)변수
edge: 노드들의 연결 여부를 담고 있는 이차원 배열로, 1의 값을 가지면 해당 노드들이 연결되어 있음n: 노드의 개수v: 시작 노드deq: 노드들을 담을 스택을 표현하기 위해collections의deque사용visited: 노드들의 재방문을 방지하기 위한 방문했던 노드들을 담아놓는 리스트current: 현재 스택에서 꺼낸 노드
⏰BFS와 DFS의 시간복잡도
- 두 방식 다 모든 노드들을 탐색하기 때문에 시간복잡도는 동일합니다.
- 그래프를 어떻게 표현하는가에 따라 시간복잡도는 달라집니다.
인접 행렬로 표현하는 경우(위의 코드)
- 모든 노드(N)에 대해서 연결되어 있는 노드를 확인하기 위해 N번의 확인을 합니다.(
for i in range(1, n+1))
인접 리스트로 표현하는 경우
- 모든 노드(N)에 대해서, 해당 노드의 인접 리스트만을 돌며 연결되어 있는 노드를 확인할 수 있기 때문에 총 간선(E)만큼의 확인을 합니다.
Reference
[알고리즘] 깊이 우선 탐색(DFS)이란
[알고리즘] 너비 우선 탐색(BFS)이란
썸네일 출처 : GIPHY