[알고리즘] 퀵 소트(Quick Sort)

Quick Sort

💡Idea

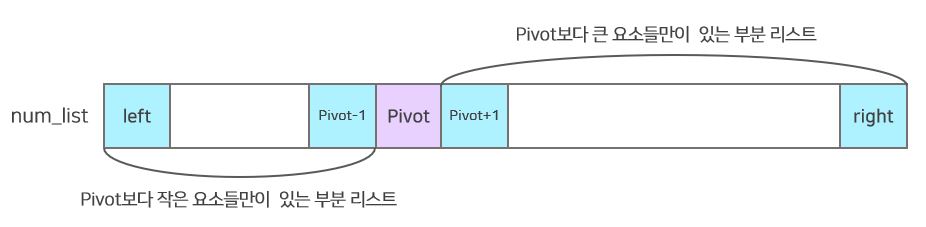
분할 정복(divide and conquer)방식을 사용하여, pivot이라는 하나의 요소를 중심으로 pivot보다 작은 요소들과 pivot보다 큰 요소들의 두 리스트로 분할하는 것을 반복하여 전체 리스트를 정렬한다.

Quick Sort 과정

1. 정렬하고자 하는 리스트 내에서 요소 하나를 선택하여 pivot으로 지정합니다.
2. pivot을 중심으로, pivot보다 작은 요소들은 pivot의 왼쪽으로, 큰 요소들은 pivot의 오른쪽으로 옮깁니다.
3. pivot을 제외한 왼쪽과 오른쪽의 리스트들을 quick sort합니다.
   • 순환 호출을 통해서 각 부분 리스트들을 정렬합니다.
   • 부분 리스트들도 동일하게 pivot을 정하고, pivot을 중심으로 두 개의 리스트로 분할하는 것을 반복합니다.

Quick Sort 알고리즘 설명

• Divide : pivot을 하나 설정하여 비균등한 크기의 두 리스트로 분할합니다.
• Conquer : 분할된 부분 리스트들을 정렬합니다. 부분 배열의 크기가 2 이상이라면, 순환 호출을 통하여 quick sort를 다시 적용합니다.
• Combine : 정렬된 부분 리스트들을 하나의 리스트로 합치는 작업이지만, Quick Sort의 경우 부분 리스트들이 제자리에 정렬되기 때문에 부가적으로 해야하는 일은 없습니다.

Quick Sort 특징

• 다른 원소와의 비교만으로 정렬을 하는 비교 정렬에 속합니다.
• 이름에서도 알 수 있듯, 평균적으로 매우 빠른 속도로 정렬을 할 수 있습니다.

💻코드1

"""
pivot을 중심으로 partition하고 두 개의 부분 리스트들에 대하여 quickSort 실행
Args:
	num_list: 정렬하고자 하는 전체 리스트
    left: 현재 리스트의 가장 왼쪽 index
    right: 현재 리스트의 가장 오른쪽 index
"""
def quickSort(num_list, left, right):
    if left >= right:
        return
    pivot = partition(num_list, left, right)

    quickSort(num_list, left, pivot - 1)
    quickSort(num_list, pivot + 1, right)

"""
pivot의 위치를 확정하고, pivot보다 작은 것들은 왼쪽에, 큰 것들은 오른쪽에 위치하도록 하는 함수
Args: 
	num_list: 정렬하고자 하는 전체 리스트
    left: 현재 리스트의 가장 왼쪽 index
    right: 현재 리스트의 가장 오른쪽 index
Return:
	pivot의 index
"""
def partition(num_list, left, right):
    p = num_list[left]
    left_index, right_index = left, right

    left_index += 1

     while True:
        while num_list[right_index] > p and right_index >= left:
            right_index -= 1
        while num_list[left_index] < p and left_index <= right:
            left_index += 1
        
        if left_index < right_index:
            # swap num_list[left_index] and num_list[right_index]
            num_list[left_index], num_list[right_index] = num_list[right_index], num_list[left_index]
        else:
            # swap num_list[right_index] and pivot(=num_list[left]), return pivot's final index
            num_list[right_index], num_list[left] = num_list[left], num_list[right_index]
            return right_index


# 정렬하고자 하는 임의의 리스트 
num_list = [4, 6, 1, 7, 5, 3, 2]

quickSort(num_list, 0, len(num_list) - 1)
print(num_list) ### 출력: [1, 2, 3, 4, 5, 6, 7]

📌코드1 설명

quickSort

• 만약, num_list의 left가 right보다 크거나 같다면(정렬하고자 하는 num_list의 길이가 1이하라면), 더 이상 정렬할 필요가 없기 때문에 그냥 return합니다.

• 그렇지 않다면, partition 함수를 통해 pivot을 선정하고, pivot을 중심으로 나뉜 두 개의 리스트를 quickSort를 통해 정렬합니다.
  1) num_list[left, pivot-1]
  2) num_list[pivot+1, right]

• 이 때 pivot의 위치는 partition을 통해 이미 정해졌기 때문에, 위 두 개의 리스트에 포함되지 않습니다.

partition 함수 설명

• 가장 왼쪽의 요소를 pivot으로 임의로 지정합니다. -> num_list[left]
  🔔이 때, 가장 왼쪽의 요소를 pivot으로 지정했다고 pivot의 위치가 가장 왼쪽인 것은 아닙니다!! pivot의 위치는 partition 함수의 마지막 부분에서 확정됩니다.

• left_index와 right_index 두 개의 변수를 통해 pivot보다 작은 것들은 pivot의 왼쪽으로, pivot보다 큰 것들은 pivot의 오른쪽으로 이동시킵니다.
  
  

partition 과정 설명

1. pivot 다음인 left_index + 1부터 시작하여 pivot보다 큰 값이 나올 때까지 오른쪽으로 이동합니다.

2. right_index부터 시작하여 pivot보다 작은 값이 나올 때까지 왼쪽으로 이동합니다.

3. left_index와 right_index의 이동이 끝난 시점에서,

   1) left_index < right_index라면 left_index에는 pivot보다 큰 값이, right_index에는 pivot보다 작은 값이 있는 것이므로 두 요소의 위치를 바꿔주면 됩니다. 그리고 아직 리스트의 모든 요소들을 보지 않았기 때문에 계속해서 이동합니다.

   2) left_index >= right_index라면, 이미 모든 리스트의 모든 요소가 pivot보다 작은 것과 큰 것으로 잘 구분되어 있는 것이기 때문에 pivot의 위치를 두 부분 리스트를 구분하는 위치로 바꿔줍니다.

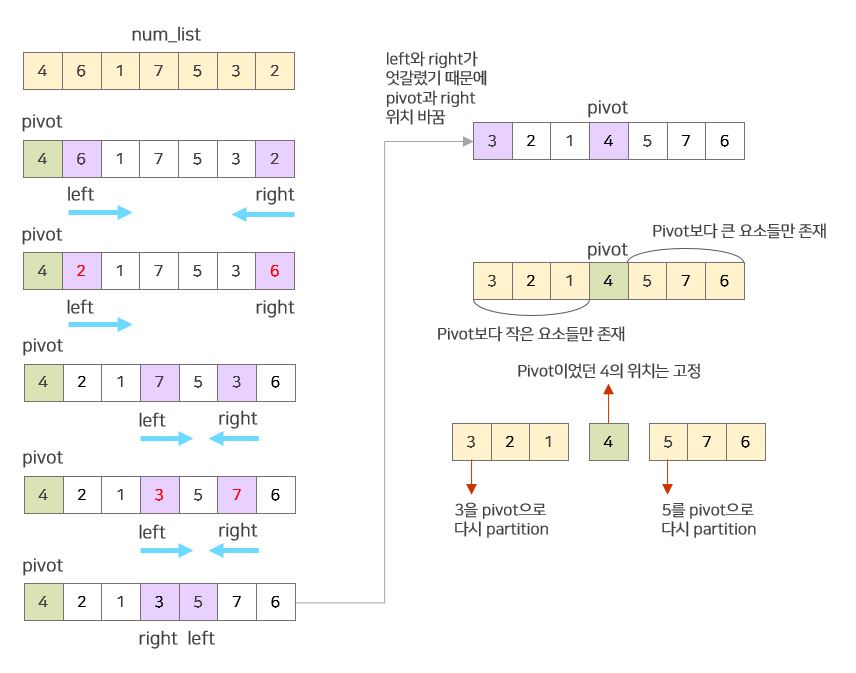
👇 처음 num_list에 partition 함수를 적용하는 예시

💻코드2

# 파이썬의 장점을 살린 퀵 정렬
def quick_sort(array):
    # 리스트가 하나 이하의 원소를 가지면 종료
    if len(array) <= 1: return array
    
    pivot, tail = array[0], array[1:]
    
    leftSide = [x for x in tail if x <= pivot]
    rightSide = [x for x in tail if x > pivot]
    
    return quick_sort(leftSide) + [pivot] + quick_sort(rightSide)

📌코드2 설명

• 사실, pivot을 선택하고 pivot보다 작은 요소들은 pivot의 왼쪽에, 큰 요소들은 오른쪽에 위치하도록 함으로써 pivot의 위치를 확정시키는 방식으로 정렬을 하기 때문에, itertools의 filter 함수나, 위와 같은 방식으로 작은 요소들과 큰 요소들을 거르는 방식으로 정렬을 할 수도 있습니다.

• 한 눈에 보기에 굉장히 직관적이고 이해가 쉽지만, 시간이 더 오래 걸린다는 단점이 존재합니다.

⏰Quick Sort 시간 복잡도(Time Complexity)

• Quick Sort의 시간 복잡도는 pivot 선택에 따라 달라집니다.

  $T(n) = T(i) + T(n - i - 1) + n$

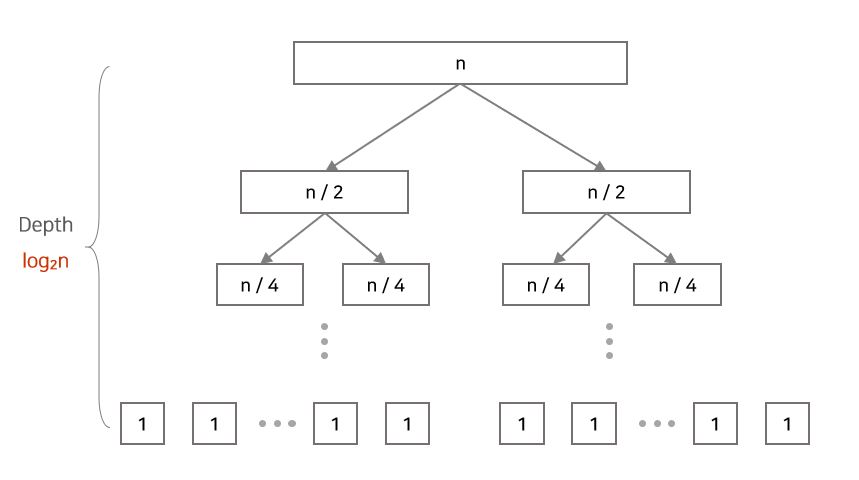
Best-case Partitioning

$O(nlog_2 n)$

$T(n) = 2T(n/2) + n$
$= 2T(n/4) + 2n$
$= …$
$= O(n log n)$

• 리스트가 균등한 길이로 나눠지는 경우
• 하나의 depth에서 약 n 번 정도의 비교 연산이 일어납니다.
  

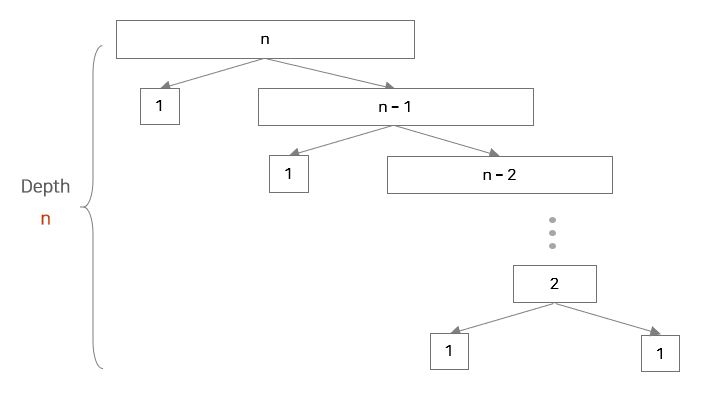
worst-case Partitioning

$O(n^2)$

$T(n) = T(n – 1) + n$
$= T(n – 2) + n – 1 + n$
$= …$
$= T(1) + \sum_{i=2}^{n} i$
$= O(n^2)$

• 리스트가 비균등한 길이로 나눠지는 경우(길이가 1인 리스트와 그 나머지 리스트로 분할되는 경우)
• 하나의 depth에서 약 n 번 정도의 비교 연산이 일어납니다.

average-case partitioning

$O(nlog_2 n)$

• 같은 시간 복잡도를 가진 다른 정렬 알고리즘과 비교해도 quick sort가 더 빠릅니다.
• 불필요한 이동을 줄이고, 멀리 떨어진 요소들을 한 번에 교환할 뿐 아니라, pivot의 위치가 한 번 결정되면 다음 정렬에서 제외되기 때문입니다.

---

Reference

[알고리즘] 퀵 정렬이란

Chapeter8. Quick Sort

파이썬의 장점을 살린 퀵 정렬

썸네일 출처: GIPHY