[알고리즘] 동적계획법(Dynamic Programming)

수영·2022년 7월 26일

DP 알고리즘

알고리즘

목록 보기

5/14

🧐동적계획법이란?

DP, 즉 동적계획법(Dynamic Programming)은 큰 문제를 작은 여러 개의 sub problem으로 나누어 해결하는 방법입니다.

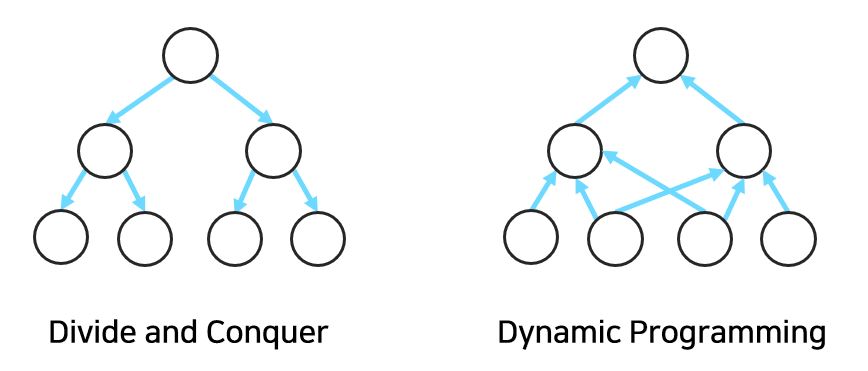
앗 그렇다면 분할 정복 방식(Divide and Conquer)이랑 다른 점이 뭐죠?!🤔

나누어진 작은 문제들이 중복되면 동적계획법, 중복되지 않으면 분할 정복 방식이라고 할 수 있습니다.

즉, 분할 정복 방식은 한 번 푼 문제와 동일한 문제는 다시 나타나지 않지만, 동적계획법은 한 번 푼 문제와 동일한 문제가 또 나타날 수 있다는 것입니다.

한 번 푼 문제와 똑같은 문제가 또 나오면 비효율적이지 않은가요?!😲

그래서 동적계획법은 Memoization을 사용합니다.
한 번 푼 계산한 값들을 저장해두고, 같은 문제가 나왔을 때 또 계산하는 것이 아니라 저장된 값을 재사용하는 것이죠!

이렇게 모든 문제들을 한 번만 계산하기 때문에 불필요한 계산을 줄이고 실행 속도를 빠르게 할 수 있습니다.

학교에서 알고리즘 강의를 들을 때 dynamic programming과 divide and conquer의 차이점을 아래와 같이 설명하기도 했습니다.

subProblem이 independent하면 Divide and Conquer
subProblem이 independent하지 않으면 Dynamic Programming

📚동적계획법을 사용하는 경우

동적계획법은 최적화(Optimization) 문제를 해결하는 것과 같습니다.

Optimization Problems

가능한 여러 개의 솔루션이 있을 수 있습니다.
각 솔루션은 값을 가지고 있습니다.
우리는 그러한 솔루션 중 가장 optimal한 값(최소 혹은 최대)을 찾고자 합니다.
찾은 솔루션을 Optimal solution이라고 부릅니다.
EX) Shortest path

동적계획법의 사용 조건

동일한 작은 문제들이 반복되어야 합니다.

동적계획법은 기본적으로 작은 문제들의 결과 값을 저장해두고, 해당 값을 재사용하여 전체 문제를 해결합니다.

그런데, 동일한 문제들이 반복해서 나타나지 않으면 재사용이 불가능하기 때문에 동적계획법을 적용할 필요가 없습니다.

그리고 당연히 동일한 문제의 결과값은 항상 정답이 같아야 합니다!!

sub problem들의 최적 솔루션이 전체 문제의 최적 솔루션을 만들 수 있어야 합니다.

예를 들어, A-B사이의 최소 거리를 구하려고 합니다.

만약 A-X와 X-B 사이의 거리가 최소 거리라면, 그 두 가지를 합친 A-X-B가 A와 B 사이의 최소 거리가 됩니다.

이와 같이, sub problem에서 구한 최적 결과가 전체 문제에서도 동일하게 적용되어 결과가 변하지 않을 때 동적계획법을 사용할 수 있습니다.

🔨동적계획법 순서

1. 최적 솔루션의 구조를 파악하라

동적계획법으로 풀 수 있는 문제인지를 확인해서 전체 문제를 작게 나누어 부분 문제들을 정의합니다.

2. 재귀적으로 최적 솔루션의 값을 정의하라

재귀적인 구조를 활용할 수 있는 관계식을 만듭니다. 즉, 점화식을 만드는 것이죠!

점화식이란, 동일한 변수 값을 넣으면 동일한 결과가 나오는 인접한 항들의 관계식을 말합니다. 점화식을 사용하면 수열을 간결하게 표현할 수 있습니다.

예를 들어 피보나치 수열의 점화식은 아래와 같습니다.

$f(n) = f(n-1) + f(n-2)$

3. bottom-up으로 최적 솔루션의 값을 계산하라

동적계획법은 top-down 방식으로도 구현할 수 있지만, 기본적으로 bottom-up 형식을 따릅니다.

가장 작은 문제부터 시작해서 전체 문제의 솔루션에 도달할 때까지 점화식을 계산하면 됩니다. 즉, Memoization을 위한 배열 d를 만들었을 때 d[0]부터 시작해 d[n]을 구하는 것입니다.

예를 들어, 피보나치 수열의 경우 아래와 같은 순서로 계산할 수 있습니다.

$f(0) = 0$
$f(1) = 1$
$f(2) = f(1) + f(0) = 1$
$...$

4. 계산된 정보들로 전체 최적 솔루션을 찾아라

3번과 연결되는 과정입니다. 점화식에 따라 계산을 하다 보면, 구하고자 하는 전체 문제의 계산 결과를 구할 수 있습니다.

만약, 피보나치 수열의 10번째 값을 알고 싶다면 아래와 같이 계산하면 됩니다.

$f(0) = 0$
$...$
$f(9) = f(8) + f(7) = 21 + 13 = 34$
$(10) = f(9) + f(8) = 34 + 21 = 55$

💻동적계획법의 구현

동적계획법의 가장 대표적인 예시인 피보나치 수열을 두 가지 방식으로 구현해보겠습니다.

Bottom-up

Bottom-up 방식은 아래에서부터 계산을 시작하여 그 결과값을 누적시켜 전체 큰 문제를 해결하는 방식입니다.
dp[0]부터 시작하여 점화식을 결과를 내어서 dp[n]까지 구합니다.
반복문을 통해서 bottom-up 방식으로 동적계획법을 구현할 수 있습니다.

def bottom_up_pibo(n):
    dp = [0] * (n + 1) #기본 기저 상태를 담은 리스트를 생성
    dp[1] = 1

    for i in range(2, n+1): # dp[2]부터 dp[n]을 구할 때까지 반복
        dp[i] = dp[i - 1] + dp[i - 2] # 점화식을 활용하여 계산

    return dp[n]

Top-down

Top-down 방식은 위에서부터 호출을 시작하여 가장 아래까지 내려간 다음, 아래의 결과를 재귀를 통하여 재활용하는 방식으로 해결합니다.
재귀 함수를 통해서 Top-down 방식으로 동적계획법을 구현할 수 있습니다.

def top_down_pibo(n, dp):
    if n <= 1: # 기본 기저 상태인 0,1이 들어오면 0과 1을 dp에 저장 후 return
        dp[n] = n
        return dp[n]

    if dp[n] > 0: # 이미 계산된 값인 경우
        return dp[n]
	
    # 계산된 적이 없는 값은 재귀를 통해 계산
    dp[n] = top_down_pibo(n - 1, dp) + top_down_pibo(n - 2, dp)
    
    return dp[n]