🧐다익스트라 알고리즘(Dijkstra)이란?
다익스트라 알고리즘은 동적 계획법(DP, Dynamic Programming)을 활용하는 대표적인 최단 경로 찾기 알고리즘입니다.
그래프에서 한 노드에서 출발하여 모든 다른 노드까지의 최단 경로를 찾는 것이죠!
노드와 노드 사이에는 weight가 존재할 수 있습니다. 노드 사이의 거리라고도 생각할 수 있는데, 다익스트라 알고리즘은 간선의 weight가 양수인 경우에만 작동합니다.
하지만 현실 세계에서 음의 간선은 존재하지 않기 때문에 다익스트라 알고리즘은 현실 세계의 문제들에 적절히 적용될 수 있습니다. 실제로 인공위성 GPS📡 등에 가장 많이 사용되고 있기도 합니다.
다익스트라 알고리즘은 그리디로 분류하기도 합니다.
매 순간 가장 짧은 거리를 선택하면서 최단 거리를 찾기 때문입니다.
🤔다익스트라 알고리즘이 DP인 이유
?? : 근데 다익스트라 알고리즘이 왜 동적계획법이죠?
👩💻 : 최단 거리는 여러 개의 최단 거리로 구성되어 있기 때문입니다!
예를 들어 A에서 C로 가는 최단 거리는, A에서 B로 가는 최단거리 + B에서 C로 가는 최단 거리로 구성되어 있다는 것입니다.
기본적으로 다익스트라 알고리즘은, 하나의 최단 거리를 구할 때 이전까지 구했던 최단 거리 정보를 그대로 사용한다는 특징이 있습니다.
그리고, 각 최단 거리는 여러 번 계산할 필요가 없죠.
👩🏫다익스트라 알고리즘의 동작
- 시작 노드로부터 모드 노드까지의 최단 거리를 우선 무한대 값으로 초기화합니다.
- 시작 노드의 최단 거리는 0으로 초기화 한 뒤, 시작 노드를 방문 처리해줍니다.
- 시작 노드와 연결되어 있는 모든 노드들의 최단 거리를 간선의 weight로 바꿔줍니다.
- 그 중 가장 거리가 짧은 노드를 선택합니다.
- 선택된 노드를 거쳐 시작 노드에서 다른 노드로 가는 최단 거리를 구합니다.
- 아직 탐색되지 않은 노드들 중 최단 거리가 가장 짧은 노드를 선택하여 방문 처리 한 뒤, 그 노드를 거쳐서 갈 수 있는 노드들의 최단 거리를 갱신해줍니다.
- 모든 노드들을 탐색할 때까지 5번을 반복합니다.
👇 예시를 통해서 함께 이해해봅시다!!
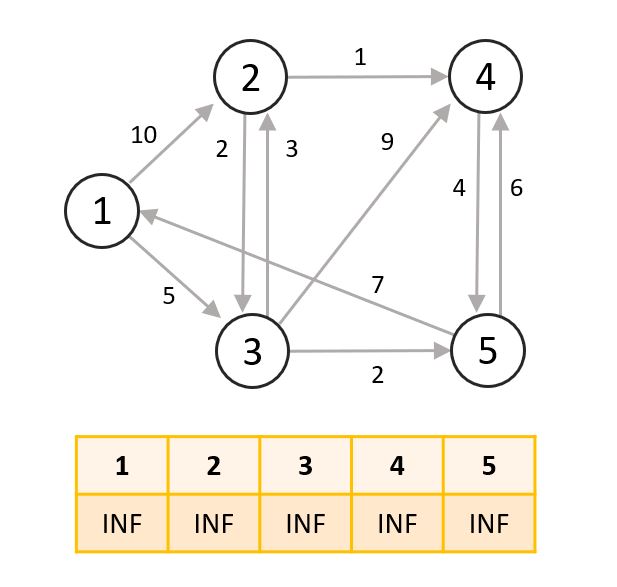
- 아래와 같은 그래프에서 1번 노드에서의 최단 거리를 찾아보려고 합니다. 우선 모든 노드로의 거리를 무한대로 초기화해줍니다.
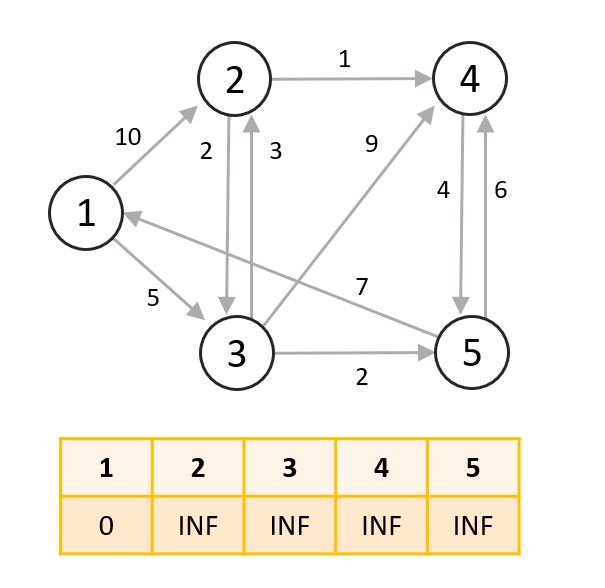
- 시작 노드인 1번 노드의 최단 거리는 0으로 바꿔줍니다.
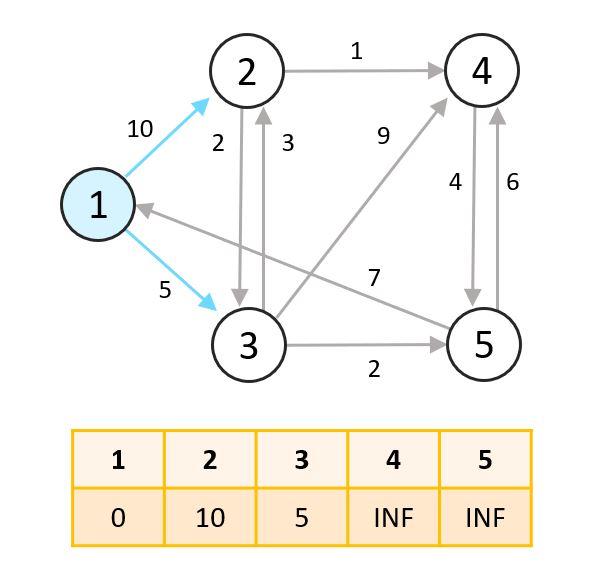
- 1번 노드에서 갈 수 있는 2번과 3번 노드로의 최단 거리를 설정해줍니다. 두 노드의 최단 거리를 연결되어 있는 간선의 weight로 바꿔줍니다.
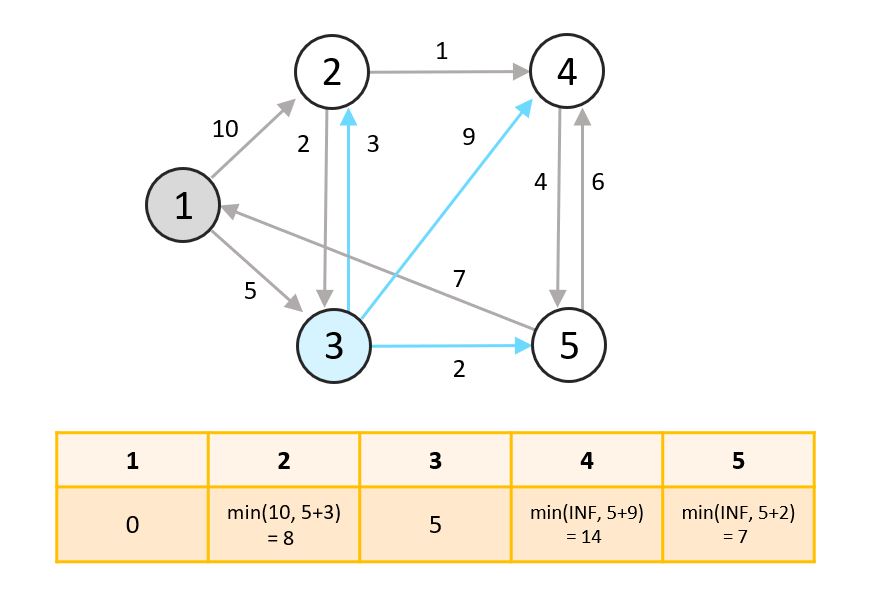
- 아직 탐색하지 않은 노드 중 최단거리의 노드는 3번입니다. 3번 노드에서 갈 수 있는 2, 4, 5번 노드의 거리를 설정해줍니다.
각 노드의 거리는현재 설정되어 있는 거리와,1번 노드로부터 3번 노드까지의 거리 + 3번 노드와 각 노드까지의 거리중 더 작은 값으로 바꿔줍니다.
예를 들어, 2번 노드는 1번 노드에서 바로 가면 거리가 10이고, 3번 노드를 거쳐가면 거리가 8이므로 2번 노드의 최단거리를 2로 변경합니다.
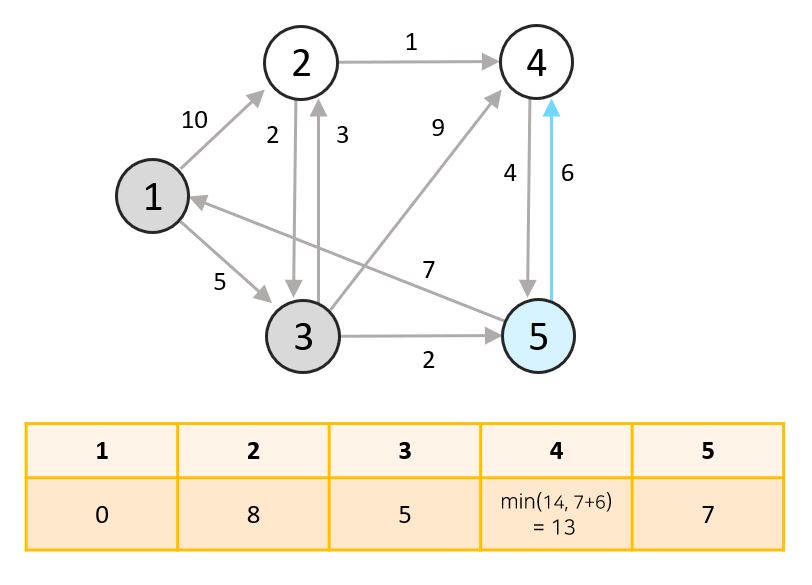
- 아직 탐색하지 않은 노드 중 최단거리의 노드는 5번입니다. 5번 노드에서 갈 수 있는 1번과 4번 중 아직 탐색되지 않은 4번 노드의 거리를 설정해줍니다.
4번 노드의 경우 3번 노드만을 거쳤을 때는 14, 5번 노드까지 거쳤을 경우에는 13이므로 최단거리를 변경해줍니다.
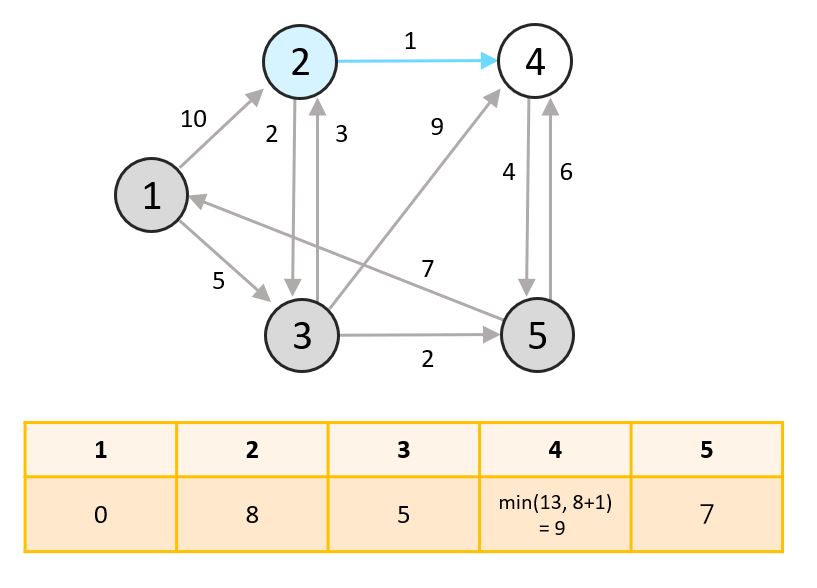
- 아직 탐색하지 않은 노드 중 최단거리의 노드는 2번입니다. 2번 노드에서 갈 수 있는 3번과 4번 중 아직 탐색되지 않은 4번 노드의 거리를 설정해줍니다.
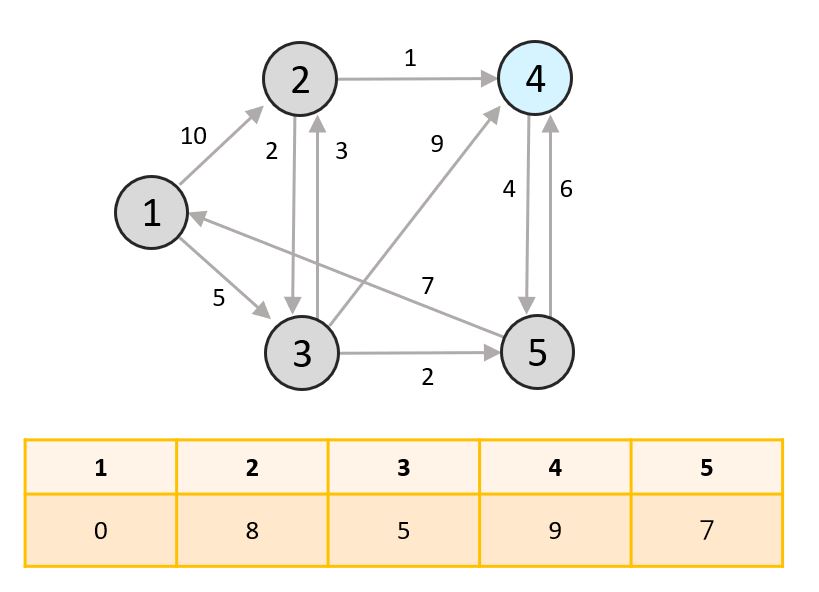
- 아직 탐색하지 않은 노드 중 최단거리의 노드는 4번입니다. 4번에서 갈 수 있는 노드 중 아직 탐색되지 않은 노드가 없으므로 종료합니다.
💻다익스트라 알고리즘 구현
다익스트라 알고리즘은 두 가지로 구현할 수 있습니다.
현재 최단 거리가 가장 짧은 노드를 찾는 방법에 따라 선형 탐색으로 구현하는 방법과 우선순위 큐로 구현하는 방법으로 나뉘어집니다.
선형 탐색의 경우 모든 노드의 거리를 살펴보면서 가장 최단 거리가 짧은 노드를 찾아내는 반면, 우선순위 큐를 사용하는 경우 pop을 통해 자동으로 거리가 가장 짧은 노드를 return해주므로 모든 노드를 탐색할 필요가 없습니다.
선형탐색으로 구현
import heapq
import sys
input = sys.stdin.readline
INF = sys.maxsize # 최대 정수값으로 무한대값 설정
V, E = map(int, input().split()) # 노드와 간선의 개수
K = int(input()) # 시작 노드
graph = [[] for _ in range(V+1)]
for _ in range(E):
u, v, w = map(int, input().split()) # u에서 v로의 간선 weight w
graph[u].append((v, w))
def dijkstraLinearSearch(start): # 선형탐색으로 다익스트라
distance = [INF for _ in range(V+1)] # 모든 거리 무한대로 초기화
visited = [0 for _ in range(V+1)] # 노드 방문 여부 0으로 초기화
distance[start] = 0 # 시작 노드의 거리는 0
for _ in range(1, V+1): # 모든 노드 개수만큼 반복
# 방문하지 않은 현재 노드 중 가장 거리가 작은 노드
minNode = distance.index(
min([d for i, d in enumerate(distance) if not visited[i]]))
visited[minNode] = 1 # 노드 방문 처리
for n, d in graph[minNode]: # 연결되어 있는 노드들에 대하여 거리 갱신
distance[n] = min(distance[n], distance[minNode] + d)
return distance
dl = dijkstraLinearSearch(K)
for i in range(1, V+1):
print(dl[i] if dl[i] != INF else "INF")
우선순위 큐로 구현
import heapq
import sys
input = sys.stdin.readline
INF = sys.maxsize
V, E = map(int, input().split()) # 노드와 간선의 개수
K = int(input()) # 시작 노드
graph = [[] for _ in range(V+1)]
for _ in range(E):
u, v, w = map(int, input().split()) # u에서 v로의 간선 weight w
graph[u].append((v, w))
def dijkstraHeapQ(start): # 우선순위 큐를 사용한 다익스트라
distance = [INF for _ in range(V+1)] # 모든 거리 무한대로 초기화
distance[start] = 0 # 시작 노드의 거리는 0
hq = [(0, start)] # 우선순위 큐에 시작노드 거리 0과 시작 노드 추가
while hq:
dis, node = heapq.heappop(hq) # 가장 작은 거리의 노드
if distance[node] < dis:
continue
for n, d in graph[node]: # 연결된 노드 중 거리가 갱신된 노드 우선순위 큐에 추가
if distance[n] > distance[node] + d:
distance[n] = distance[node] + d
heapq.heappush(hq, (distance[n], n))
return distance
dh = dijkstraHeapQ(K)
for i in range(1, V+1):
print(dh[i] if dh[i] != INF else "INF")
⏰ 시간복잡도
-
선형탐색의 경우
시간 복잡도는 입니다.
방문하지 않은 노드들 중에서 최단 거리가 짧은 노드를 선택하기 위해 매 단계마다 노드의 개수만큼 거리를 순차탐색해야 하기 때문입니다. -
우선순위 큐의 경우
시간복잡도는 입니다.
우선순위 큐에 들어가는 노드의 개수는 최대 개입니다. 따라서, 탐색하는 노드의 개수 역시 최대 개가 됩니다.
결국 의 시간복잡도를 가지게 되는데, 는 보다 항상 작기 때문에 입니다. 따라서 하나의 간선에 대해 걸리는 시간복잡도는 이므로 위와 같은 시간복잡도가 나옵니다.