[알고리즘] 최대공약수(GCD) 구하기-유클리드 호제법(Euclidean-algorithm)

수영·2022년 8월 4일

목록 보기

6/14

유클리드 호제법은 어떤 두 수의 최대공약수를 구하는 알고리즘 중 가장 유명한 알고리즘 중 하나입니다.

유클리드가 기원전 300년경에 발견한 가장 오래된 알고리즘이며, 두 수가 서로 상대방의 수를 나누어서 원하는 수를 결과로 얻게 되는 방법인 호제법을 사용합니다.

유클리드 호제법은 아래와 같은 성질에 따라 최대공약수를 구합니다.

어떤 두 수 $M, N$ 이 있을 때( $M>N$ ), $M$ 과 $N$ 의 최대공약수는 $M\;mod\;N$ 과 $N$ 의 최대공약수와 동일하다.

위에서 말한 유클리드 호제법의 성질에 따라 최대공약수를 구해봅시다!

1071과 1029의 최대공약수는 무엇일까?🤔

1071 $mod$ 1029 = 42
1029 $mod$ 42 = 21
42 $mod$ 21 = 0

간단히 말해, 유클리드 호제법으로 최대공약수를 구하려면 두 수중 큰 수를 작은 수로 나머지 연산을 하는 $mod$ 연산을 반복하면 된다!!

그래서, 어떻게 저런 성질이 성립하는데?!🤷‍♀️

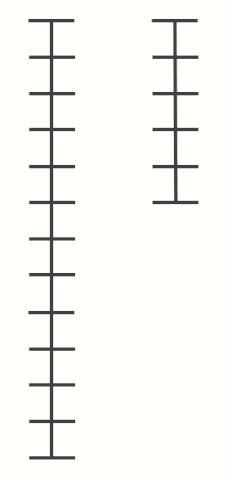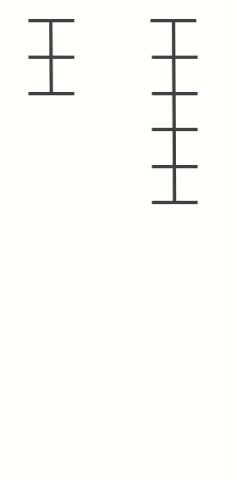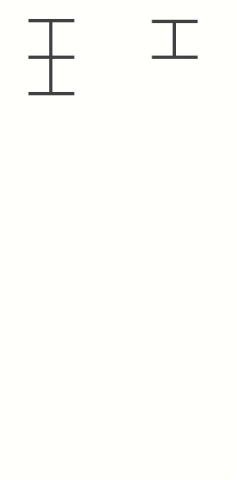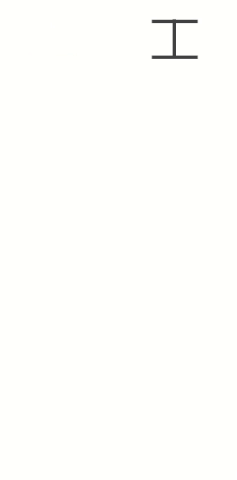
위의 그림을 보면 조금 쉽게 이해할 수 있습니다.
임의의 수 $M$ 과 $N$ 을 계속해서 $mod$ 연산하는 과정을 나타낸 그림입니다.

$M$ 과 $N$ 을 막대로 표현하고, 막대의 한 칸을 $M$ 과 $N$ 의 최대공약수인 $G$ 로 하여 막대를 나누어 표현해보았습니다.

과정을 잘 살펴보면, 나머지들도 계속해서 $G$ 를 최대공약수로 가짐을 알 수 있습니다.

계산식으로도 유클리드 호제법을 이해할 수 있습니다.

어떤 수 $M$ 을 $N$ 으로 나눈다면 아래와 같이 표현할 수 있다.

$M = NQ + R$
$M$ 과 $N$ 의 최대공약수를 $G$ 라고 한다면, $M = mG$ , $N=nG$ 로 표현할 수 있다.
해당 식을 사용하여 나머지인 $R$ 을 표현한다면 아래와 같다.

$mG = nG Q + R$
$R = mG - nGQ = G(m-nQ)$
나머지 $R$ 역시 최대공약수인 $G$ 를 가지고 있으니, $M$ 과 $N$ 의 최대공약수는 $N$ 과 $R$ 의 최대공약수와 같다고 할 수 있다.

import sys
M, N = map(int, sys.stdin.readline().split())

while(N): # 나머지가 0이 될 때까지 반복
    r = M % N 
    M = N
    N = r
print(M)

import sys
M, N = map(int, sys.stdin.readline().split())

def Euclidean(M, N):
    return Euclidean(N, M % N) if N else M

print(Euclidean(M, N))

하고 싶은 건 그냥 죽도록 합니다

알고리즘