[ML]최적화 알고리즘 2가지(optimization algorithm)

parameter를 측정하는 데에는 크게 두 가지 방법이 있습니다. 1) gradient descent로 iteration을 통해 최적화하는 방법과, 2) Normal equation을 통해 최적해를 결정적으로 구하는 방법입니다.

1) gradient descent 기법을 통해 최적화하는 방법

모델을 가설 함수에 기반하여 Loss function 을 정의합니다. 아래와 같습니다. (아래 설명할 내용은 편의를 위하여 $h_\theta(x) = \theta_1x + \theta_0$ 을 가정하겠습니다.)

우리가 모델을 최적화(optimize)한다는 것은 위 Loss function을 최소화하는 것과 같습니다.

우리가 특정 함수의 최솟값을 찾는 대표적인 방법은 무엇이 있을까요? 바로 미분입니다. 미분한다는 것은 기울기(gradient)를 측정한다는 의미이고, 이 gradient값에 기반하여 최소 지점으로 하강(descent)합니다.각 parameter값에 대한 편미분(partial derivative)를 통하여 최적화하는 gradient descent 기법의 식은 아래와 같습니다.

여기서 $:=$ 연산자는 할당(assignment)를 의미합니다.

(1) $\alpha$

$\alpha$ 는 learning rate로서, update 시 어느 정도 단위로 움직일지 결정하는 step size이자 엔지니어가 직접 설정해주어야 하는 hyperparameter입니다.(일반적으로 0.01~0.1 의 값을 취합니다.) $\alpha$ 값이 크다면 한번 update 시 더 크게 움직이고, 작다면 그 반대입니다. 그렇기 때문에 적절한 값을 골라 주는 것이 중요합니다.

(2) $\frac {\partial}{\partial \theta_j}J(\theta_0, \theta_1)$

$\frac {\partial}{\partial \theta_j}J(\theta_0, \theta_1)$ 는 update시 parameter값이 이동할 방향과 크기를 결정합니다. 설명을 위해 아래 그림을 잠시 살펴보겠습니다.

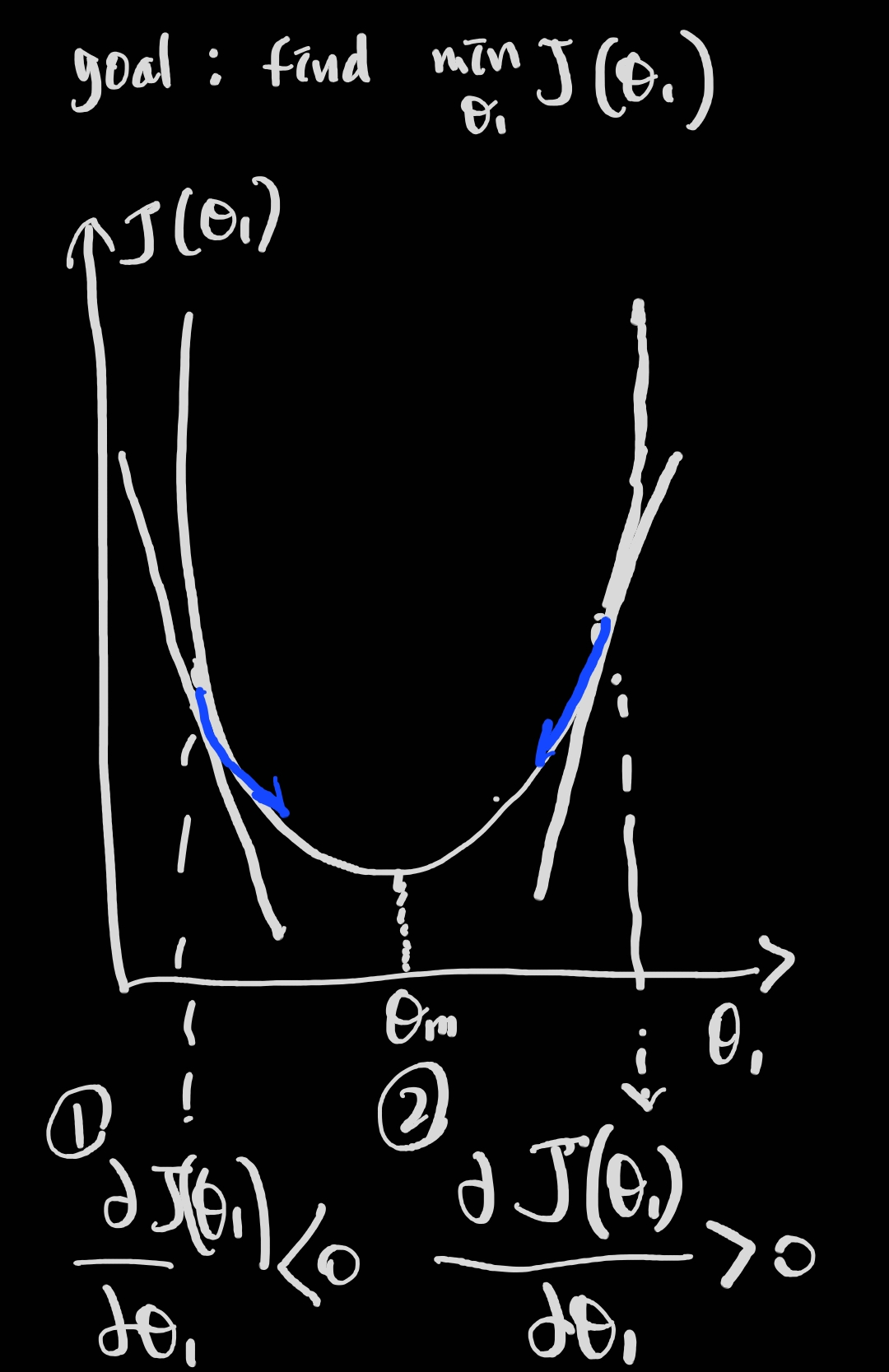
[simple graphical view of gradient descent algorithm]

시각화를 위해 더 단순화하여 Loss function의 parameter값을 하나로 놓고 보겠습니다( $\theta_1$). 그렇다면 Loss function은 위와 같이 정의됩니다($J(\theta_1)$). 이러한 이차원 좌표계에서 우리는 단순화된 하나의 이차함수를 연상하여 볼 수 있습니다(실제로는 여러 극값을 가진 매우 복잡한 함수가 될 것입니다). 거듭 이야기하자면 우리의 목표는 Loss function이 최소가 되는 parameter 값을 구하는 것입니다(그림의 $\theta_m$ 에 해당).

함수의 미분값은 기울기(gradient) 입니다. 화살표 방향에 유의하면서 아래 내용을 이해해 봅시다.

(i) 그림에서 ①번의 경우, 기울기는 음수이며 $\frac {\partial}{\partial \theta_1}J(\theta_1)<0$ 이 됩니다. 이는 $-\alpha \frac {\partial}{\partial \theta_1}J(\theta_1) >0$ 을 의미하며, 양수 방향으로 parameter 값을 update 하게 됩니다.

(ii) 그림에서 ②번의 경우, 기울기는 양수이며 $\frac {\partial}{\partial \theta_1}J(\theta_1)>0$ 이 됩니다. 이는 $-\alpha \frac {\partial}{\partial \theta_1}J(\theta_1) <0$ 을 의미하며, 음수 방향으로 parameter 값을 update 하게 됩니다.

추가적으로 기울기 경사가 급할수록 update하는 차이값은 커진다는 것을 위 내용을 통하여 이해하여 봅시다.

최종적으로, 적절한 learning rate 를 설정하여 학습을 시키고 최적화시킨다면 우리가 원하는 parameter 값으로 수렴할 수 있게 됩니다. 그렇지 않고 learning rate를 너무 크게 설정하면 발산하게 되고, 너무 작게 설정하면 최적화 과정에서 지나치게 오랜 시간을 소요하게 됩니다.

다시 위 식을 확인하여 봅시다. parameter개수가 많아져 n+1개의 일반적인 경우에 대하여 이야기한다면, 각각 편미분에 의한 gradient계산과 update가 이루어질 것입니다. 주의해야 할 점은 $\theta_0, \theta_1, ..., \theta_n$ 모두 동시에 update 되어야 한다는 것입니다. 다시 말해, $\theta_0$ 를 update 한후 가설 함수에 연산을 적용해버리면 목표 달성에 문제가 생기게 됩니다.

(3) 장단점

• Gradient Decsent 과정은 iterative 한 방법을 통해 해를 찾아나가기 때문에, 데이터 양이 매우 큰 경우 계산량 측면에서 효과적이라는 장점이 있습니다.
• 단점은 local minima (국소 최소점) 에 빠질 위험이 있다는 것입니다. 우리가 계산할 Loss function의 식은 위의 그래프처럼 간단한 모양이 아니기 때문에, 다양한 극소점이 존재할 것이며 수렴된 지점이 global minimum(전역 최소점)이라는 보장이 없습니다. 이에 유의하여 모델을 최적화하는 것이 필요합니다.

2) Least squares method(Normal equation을 활용하는 방법)

iterative 하게 최소지점으로 나아가는 것이 아닌, 주어진 데이터를 통하여 deterministic하게 parameter 값을 결정할 수 있습니다. (단, $X^TX$ 가 역행렬이 존재하여야 쓸 수 있는 방법입니다.) n이 크면 매우 느려지지만, (n=10,000 이상일 때) 그렇지 않다면 활용해 볼 수 있는 방법입니다. 이를 Least square method라고 하며, 미분하여 0이 되는 지점을 이야기합니다. 여기서 matrix X는 $(d,n)$의 모양을 가정합니다. $d$는 데이터의 차원, $n$는 데이터 개수를 의미합니다.

위 식에서 예측값 $\hat y$의 MSE를 최소화하는 식은 아래와 같이 표현 가능합니다.

위 식을 $\theta$에 대하여 미분한 후, 0이되는 값을 계산하면 아래와 같은 식으로 정리되며, 명시적인 해를 구할 수 있습니다. 이를 Normal equation이라고 하며, 최적해를 한 번에 찾을 수 있는 방법입니다.

Hessian Matrix

$\theta$ 의 hessian matrix를 구하고, 그것이 특정 지점에서 positive definite 일 경우 그 지점이 local minimum 등인지를 알 수 있습니다.