추천시스템 알고리즘 중 하나인 MF에 대하여 공부해 봅시다.
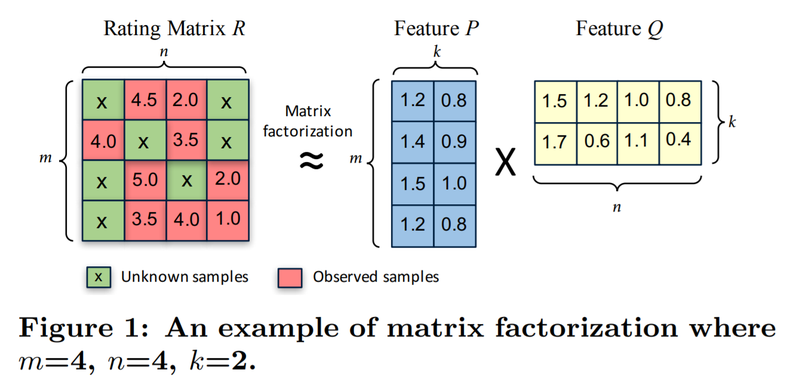
[- 출처: CuMF_SGD: Fast and Scalable Matrix Factorization(https://arxiv.org/pdf/1610.05838.pdf)]
핵심 : (m,n) 사이즈의 행렬 R을 (m,k) 사이즈의 행렬 P와 (k,n) 사이즈의 행렬 Q로 분해한다면 R이란 그저 P와 Q의 행렬곱으로 표현 가능할 수 있다.
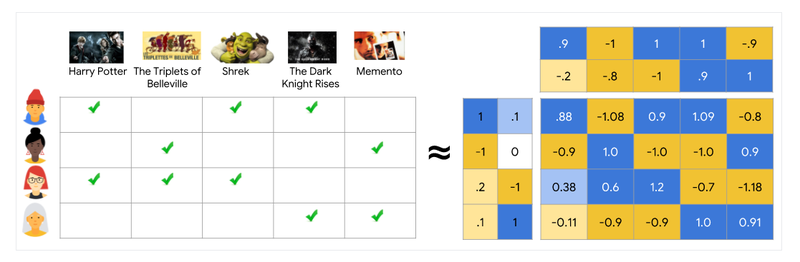
[출처: https://developers.google.com/machine-learning/recommendation/collaborative/matrix]
그림을 보면서 이해해 봅시다.
m=4,n=5,k=2입니다. 개별 벡터는 k=2인 하나의 임베딩 벡터로 생각해 봅시다.
:사용자에 대한 벡터(m,k)
: n개의 영화에 대한 벡터(k,n)
은 바로 빨간 모자를 쓴 첫 번째 사용자의 특성(Feature) 벡터
는 해리포터 영화의 특성 벡터
따라서 빨간 모자를 쓴 사람의 해리포터 영화 선호도는,
이 되며 이는 m,n 행렬의 0,0 원소가 됩니다.
