신찬수 교수님의 유튜브 자료구조- 균형이진탐색트리를 공부하고 참조하여 본 글을 작성한다.
균형 이진탐색트리 (Balanced Binary Search Tree)
- 균형 이진탐색트리: 오른쪽 서브트리의 높이와 왼쪽 서브트리의 높이차가 1이하인 이진탐색트리를 말한다.
- 일반적 이진검색트리에서 트리구조가 한 쪽으로 치우치는 경우가 발생 가능. 이를 방지하기 위해 rebalancing을 수행. (AVL 트리, B 트리, Red-black 트리 등)
- Rotation
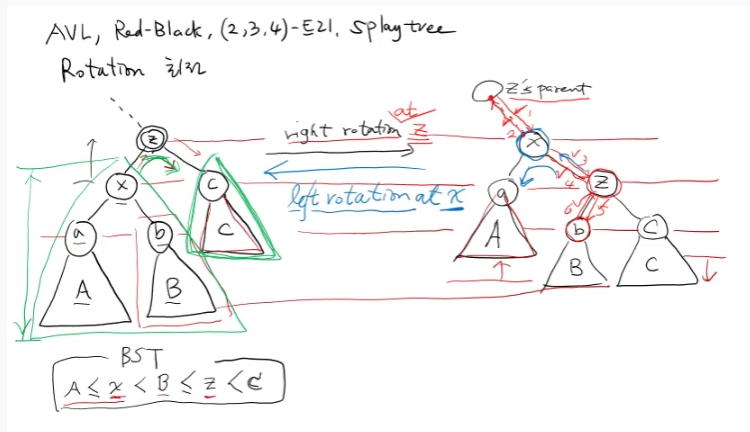
z를 기준으로 right rotation 할 떄와,
x를 기준으로 left rotation 할 때를 보여준다.
BST 크기 순서가 A<=x<B<=z<c 이므로, 이 서열을 유지해주면서 rotation을 해주어야 한다.
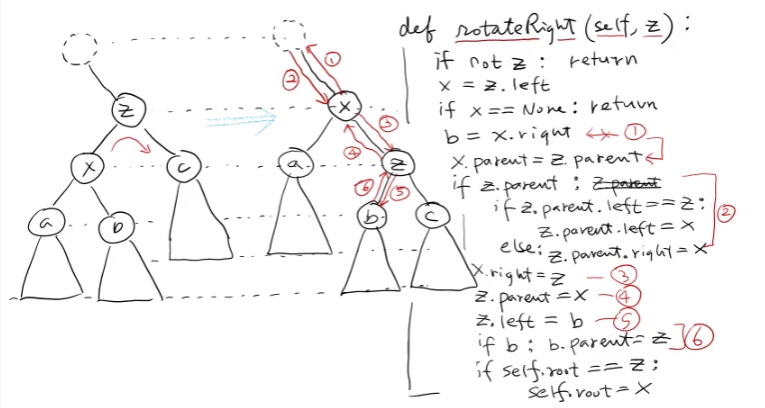
->O(1) 시간에 rotation은 가능
AVL 트리
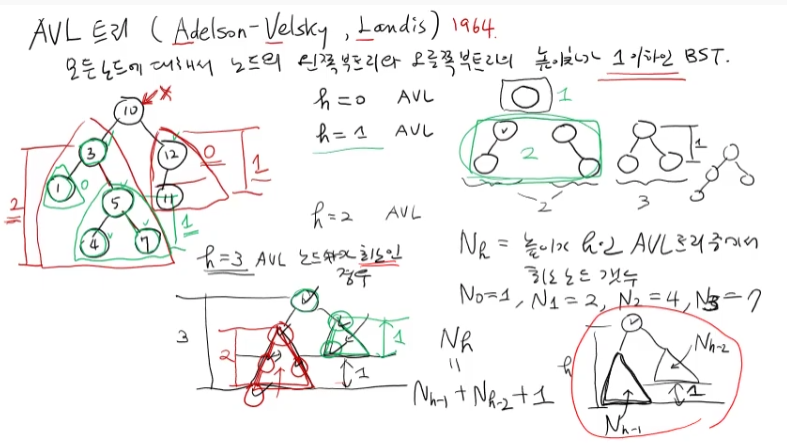
- 모든 노드에 대해서 노드의 왼쪽 서브트리와 오른쪽 서브트리의 높이차가 1이하인 BST
- 이진 탐색 트리가 최상의 성능을 얻으려면 트리의 균형을 유지해야 한다.
- Nh= 높이가 h인 AVL트리 중에서 최소 노드 개수라 할때,
N(h)=N(h-1)+N(h-2)+1 이라는 점화식을 얻을 수 있다. - 불균형 상태일 때, (양쪽 서브트리 높이 차가 2 이상인 경우) rebalancing 을 한다.

rotation case
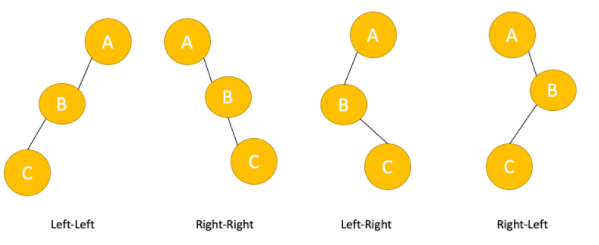
불균형 발생 노드가 a 일때, rotation을 사용해야할 케이스 4가지.
(출처: https://velog.io/@soonbee/AVL-Tree%EB%A5%BC-%EC%95%8C%EC%95%84%EB%B3%B4%EC%9E%90)
- left-left
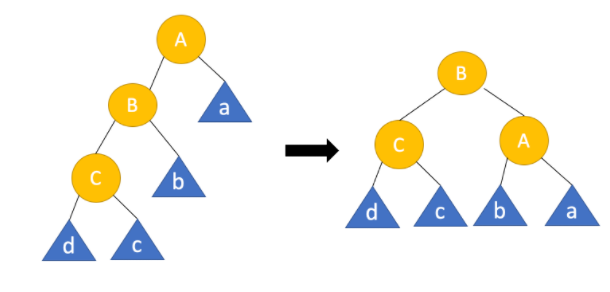
A노드 기준으로 right rotation 진행
- right-right
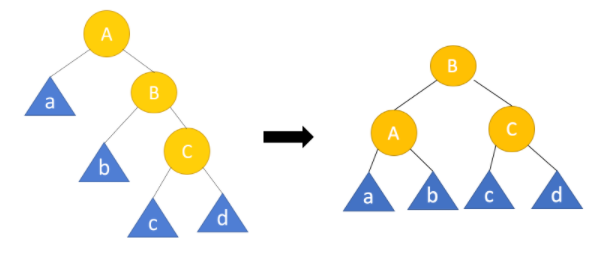
A노드를 기준으로 left rotation을 진행
-
left-right
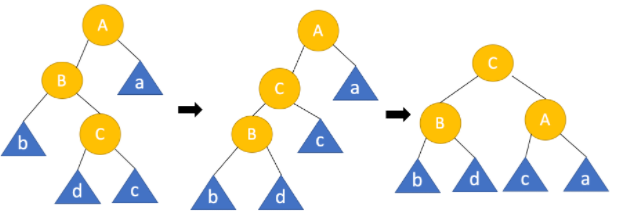
두 단계를 거쳐야 한다. 우선 B 노드 기준으로 left rotation 후, A노드 기준으로 right rotation 진행. -
right-left
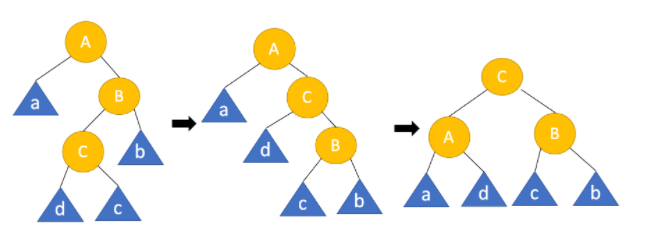
두 단계를 거쳐야 한다. 우선 B 노드 기준으로 right rotation 후 A 노드 기준으로 left rotation 진행
AVL 트리의 삽입 연산
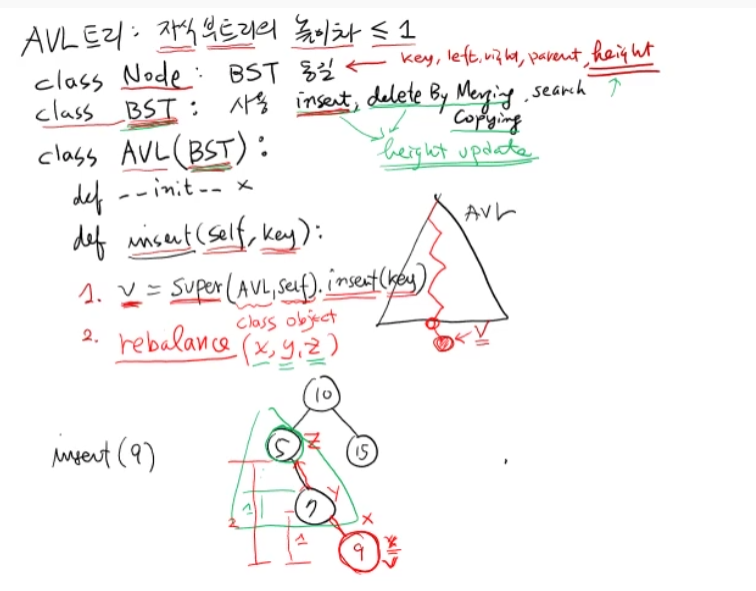
- AVL 트리의 경우, 위의 사진과 같이 9가 삽입될 때, avl의 조건이 깨지게 된다. 이때, rebalance 과정이 필요하다. 위의 x, y, z에서 z는 처음으로 avl조건이 깨진 노드를 뜻한다.
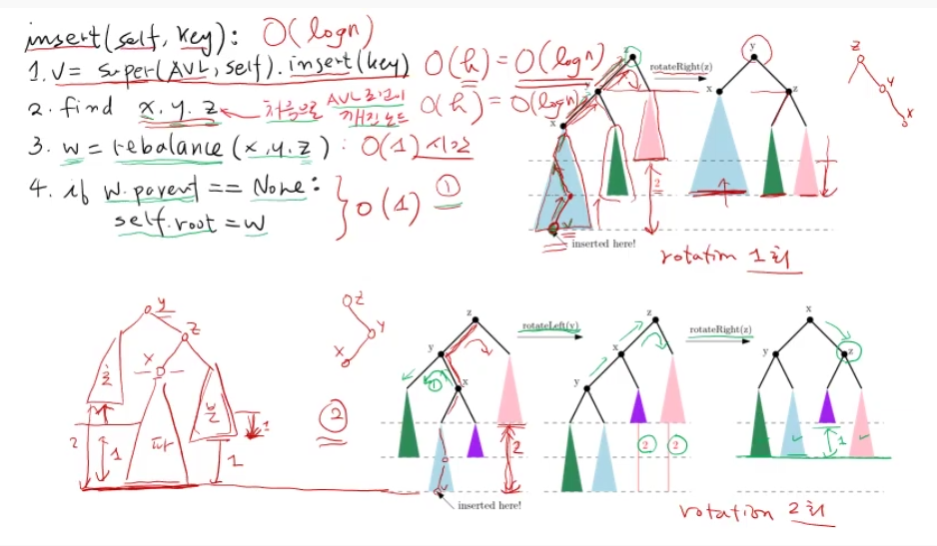
- insert 에서는 1회 또는 2회의 로테이션을 하면 AVL 트리를 유지가능.
AVL 트리의 삭제 연산
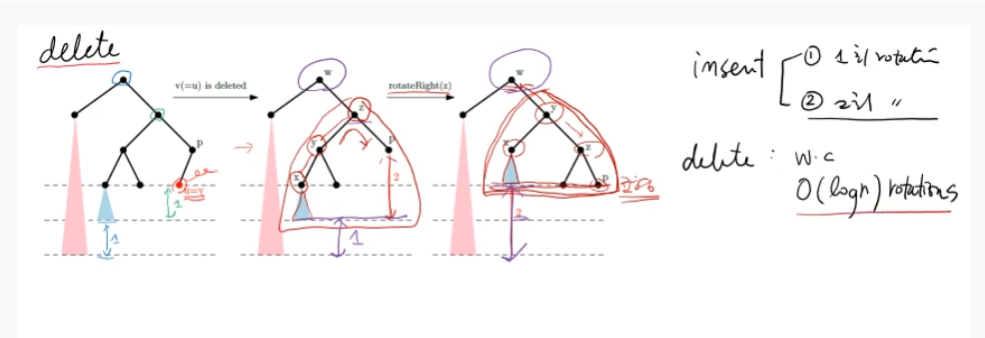
- delete 때는 h 만큼 rotation을 할 수 있음
정리
- 높이 <=2logn=O(lgn)
- insert: 노드 삽입 O(lgn), rebalance-1회 or 2회 회전
- delete: 노드 제거 O(lgn), rebalance- 매 level 마다 O(lgn) 회전
reference
https://velog.io/@soonbee/AVL-Tree%EB%A5%BC-%EC%95%8C%EC%95%84%EB%B3%B4%EC%9E%90
