220411_TIL (Vector / Matrix)

이번 주는 선형 대수를 공부한다.
그 시작으로 Vector, Matrix에 대해서 공부했는데, 처음 듣다보니 헷갈리는 개념이 많이 있었다. 지금은 기본적인 개념은 이해를 하긴 했는데, 과연 내일의 내가, 일주일 뒤의 내가, 한 달 뒤의 내가 이걸 기억할 수 있을까 매우 우려스럽다!

그리하여 아예 배운 것을 정리하는 식으로 TIL을 작성해본다.

Key words

• 벡터와 매트릭스의 기본 연산
• Identity Matrix
• Determinant (⭐)
• Inverse Matrix

---

차원 (dimension)에 대해서 짚고 넘어가자.

지금까지 '차원'에 대해서 참으로 많이 이야기 했는데, 이 '차원'이 의미하는 바가 상황에 따라 다르게 쓰여 헷갈리고 정확히 이해하지 못하고 있었던 것 같다. 마침 오늘 QnA 시간에 한 번 정리하고 넘어갔다.


Data Structure 측면에서

• 1차원: 행과 열의 구분 없이 데이터를 일렬로 나열한 상태
• 2차원: 행과 열이 있는 데이터 프레임 형태
• 모두 요소 간 순서가 있다!

벡터에서

• n차원의 벡터는 컴포넌트라고 불리는 n개의 원소를 가지는 순서의 모음이다. (= 스칼라의 모음)
• 여기서 말하는 차원이란 벡터의 원소의 개수다!

matrix에서

• 매트릭스에서 말하는 차원이란 shape을 의미한다.
• 근데 나중에 머신러닝에서는 feature의 수를 차원이라고도 한다.
• 피쳐 기준으로는 4차원이고, 매트릭스 기준으로는 2 by 4 shape을 갖는다~ 이런 식으로 상황에 따라 다양하게 표현 가능!

스칼라

스칼라와 벡터는 선형 대수를 구성하는 기본 단위이다.

• 스칼라는 쉽게 단일의 숫자라고 생각하면 된다. 실수와 정수 모두 가능하다.
• 벡터 또는 매트릭스에 곱해지는 경우, 안의 요소가 이 스칼라에 곱해진 값으로 나오게 된다.
  
  

벡터

벡터의 정의는 위에서 말한 걸 다시 가져온다.

• n차원의 벡터는 컴포넌트라고 불리는 n개의 원소를 가지는 순서의 모음이다. $\vec{v}$ 이렇게 소문자 위에 화살표를 갖는 걸로 표시한다.
• 물리학에서 말하는 벡터, 컴퓨터 공학에서 말하는 벡터의 개념이 조금씩 다르다고 하는데, 데이터 과학에서 벡터란 숫자 자료를 배열한 것이다
  • 즉, 우리는 데이터 분석을 하면서 많은 숫자들을 보게 되는데, 그 배열을 시각적으로 개념화하기 좋은 방법을 제공해준다는 것이 우리가 선형대수학을 배우는 이유다.
• 데이터프레임의 행/열로써 벡터를 말할 수도 있는데, 예를 들어 2X2 데이터 프레임이 있다고 했을 때 각 열을 열벡터, 각 행을 행벡터라고 부를 수도 있다.
  
  

벡터에 대해 꼭 기억해야 할 것! (헷갈려어~)

• 벡터의 길이(length): 벡터의 차원 수와 동일하다.
• 벡터의 크기(norm, maginitude): 길이를 나타낸다.
  - 벡터는 아래와 같이 뻗는 크기와 방향이 있는데, 쉽게 말해 저 선의 길이가 norm이라고 생각하면 된다.
  - 즉, 벡터의 norm이란 모든 원소의 제곱을 더한 후 루트를 씌운 값이다. (피타고라스의 정리를 생각하면 기억하기 쉽다)
  (정확히 말해 이건 $L_2$ norm이다. $L_1$ norm은 각 요소의 절대값을 모두 더한 것인데 당장은 $L_2$ norm이 더 중요하다고 한다.)
  
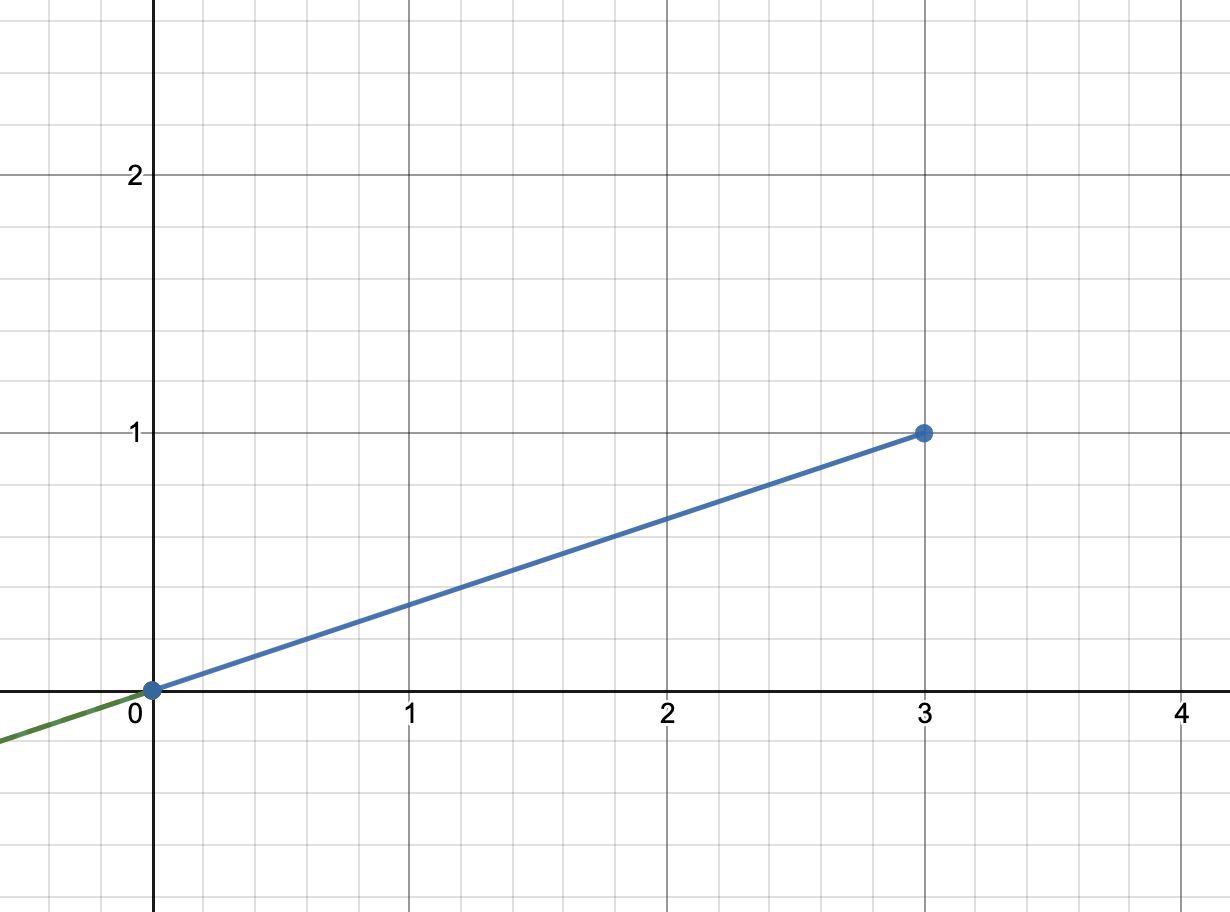
• 참고로 벡터의 크기는 0보다 같거나 크다.
  
  

벡터의 내적(dot)
두 벡터 $\vec{a}$ 와 $\vec{b}$ 의 내적은, 각 구성요소를 곱한 뒤 합한 값과 같다.

• 대체 내적이란 뭔가 싶었는데, 우선은 그냥 덧셈, 곱셈이 있는 것처럼 벡터 연산의 한 종류로 내적이 있구나~ 생각하면 될 것 같다.
• 예시)
  • a= [1,2,3], b = [2,3,4]라면 v $\cdot$ x은 1x2 + 2x3 + 3*4 를 하여 20이 된다.

Numpy에서는 np.dot(v1, v2) 함수를 쓰면 바로 계산이 쉽게 된다!

매트릭스

행과 열을 통해 배치되어 있는 숫자들이다.
데이터 프레임을 통해 자주 봐왔기 때문에 익숙한 형태이다.

Matrix Multiplication

• 행렬곱의 결과는 헹렬로 나온다. (참고로 벡터의 곱은 스칼라로 나온다) 앞 행렬의 '행의 수'와 뒤 행렬의 '열의 수'가 맞는 경우에만 할 수 있다.
• 예시)
  

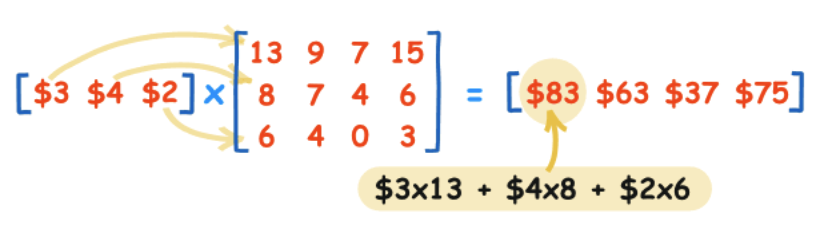
Transpose

• 행과 열을 바꾸는 걸 의미하는데 이전에 데이터 프레임 다룰 때도 썼던 개념이다.
• 3x3 매트릭스의 transpose는 어떻게 되는걸까? 헷갈렸다.
• 예를 들어, 이런 매트릭스가 있다고 했을 때 이걸 transpose 하면?
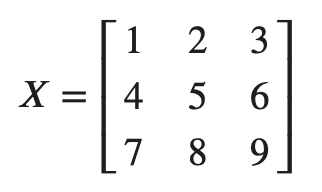
• 각 요소의 위치를 생각해보고 뒤바꾸면 된다. 예를 들어, 2는 (1,2)니까 (2,1)에 있는 4와 자리를 바꾸면 된다!
  
  

정사각 매트릭스 (Square Matrix)

• 행과 열의 수가 동일한 매트릭스를 말한다. (2X2, 3X3 etc..)
• Diagonal (대각선)
  • 대각선 부분에만 값이 있고 나머지는 전부 0
• Identity (단위 매트릭스)
  - Diagonal 매트릭스 중에서, 모든 값이 1인 경우이다.
  
  
  

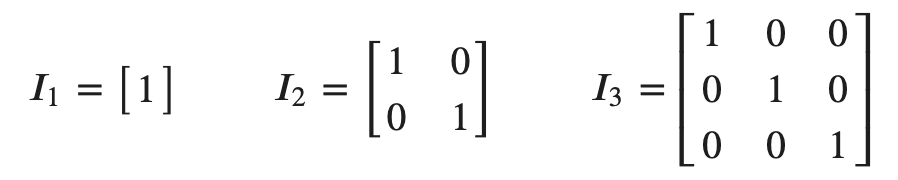
Determinant (중요!!!)
행렬식은 모든 정사각 매트릭스가 갖는 속성이다.

• 𝑑𝑒𝑡(𝐴) 혹은 |𝐴| 로 표기된다.
• 2X2 matrix 기준으로, (AD-BC)로 계산하면 된다.
• 예시) 바로 위 그림의 $I_2$를 예시로 해보면, $1*1 - 0*0$을 한 값이 바로 행렬식이다.
• 3차원 이상은 직접 풀 필요는 전혀 없을 것 같다. 왜냐하면? numpy의 np.linalg.det()로 구할 수 있기 때문이다!
• 행렬식이 0인 정사각 매트릭스는 특이(singular) Matrix 라고 부른다. 이 경우에는 매트릭스의 행과 열이 선형의 의존관계가 있다~ 라고 표현할 수 있다.
  - 특이 매트릭스의 행렬식이라는 건 결국 N차원 공간의 벡터들로 구성된 도형의 부피인데, 그게 0이라는 거 두 벡터가 동일선상에 있다는 뜻이기 때문.
  
  

Inverse
2X2 매트릭스는 아래와 같은 공식이 있다.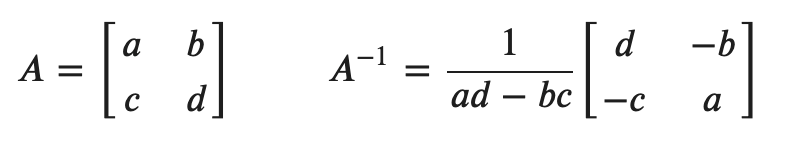

• 참고로 행렬과 그 역행렬을 곱하면 항상 1 (단위 매트릭스)가 된다! 선형대수에는 매트릭스의 곱은 있지만 나눗셈은 없기 때문에 이 역행렬을 이용해서 연산을 하는 경우가 있는 것 같다. (cramer's rule이라고 다른 방법도 있긴 하지만 역행렬 곱하는 식이 가장 쉽다고 여겨지는 것 같다.)
• 당연하지만 1차원 매트릭스는 inverse할 수 없다.
  
  

그 외 array 재밌었던 것

numpy는 다차원 배열과 배열 연산을 수행하는 다양한 함수를 제공하는데, array를 이용하면 벡터 및 행렬 연산에 매우 편리하다.

list와는 연산을 할 때 차이가 있다고 생각하니 쉬웠다.
예를 들어,

a = [1,2,3]
b = [3,4,5] 

print(a + b)
#[1,2,3,3,4,5] 

list는 더하면 위와 같이 나오지만, array 형태라면, [4,6,8] 이런 식으로 연산이 되어서 나온다.

즉, array로 하면 각 요소별로 곱셈, 제곱, 루트 씌우기 등의 연산이 매우 쉬워진다!
-추가 예) abs(a) 를 하면 그 안의 모든 요소에 절대값을 먹일 수 있다.