220413_TIL / (Eigenvector, Eigenvalue, PCA)

오늘은 Eigenvector, Eigenvalue의 의미를 이해하는데 참으로 헤맸다. 그러니 자연스럽게 PCA도.. 😷 지금 이해하고 있는 걸 잊지 않고 싶다! 힘들었지만, 오늘 드디어 선형대수가 데이터 사이언스에서 어떤 의미를 가지는지, 왜 지난 며칠간 벡터며 매트릭스며 배웠는지 이유를 알 수 있는 날이어서 나름 뿌듯하다.

(아래 정리하는 내용에는 정확한 수학적 정의나 산출 방식을 담고 있지 않다. 개념과 활용의 관점에서만 기록해둔다. 어차피 우리에겐 파이썬의 위대한 라이브러리가 함께한다)

Key words

• Vector Transformation
• eigenvector, eigenvalue
• PCA (Principle Components Analysis, 주성분 분석) (⭐)

---

# Vector Transformation

Vector Transformation의 정의는 아래와 같다. (2차원 공간)

• 벡터의 선형 변환은 임의의 두 벡터를 더하거나 혹은 스칼라 값을 곱하는 것.
• 
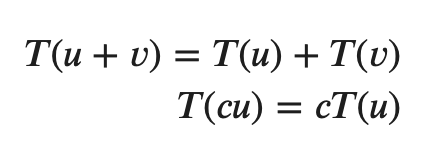
• 또 다른 표현으로는 한 점을 한 벡터공간에서 다른 벡터 공간으로 이동시키는 이동 규칙을 정의하는 함수다.

쉽게 생각하자!

• 위 정의에서 키워드는 '더하거나 혹은 곱한다'이다. 선형이기 때문에 이 둘 말고는 없다. 선형 변환이라고 생각하자.
• 즉, 임의의 벡터에 다른 벡터나 스칼라, 혹은 매트릭스를 곱해서 또 다른 벡터로 변환하는 것이라고 생각하면 된다.
• 그냥 주어진 벡터를 씹고(더하고) 뜯으며(곱하며) 맛보는 거(새로운 벡터 생성)라고 이해하면 될 것 같다.
• 선형변환을 하게 되면, x,y좌표에서 원점을 기준으로 좁게 모여있는(분산이 작은) 데이터를 길게 늘어뜨려서 볼 수 있는 장점이 있다.

이게 오늘 공부한 거랑 무슨 상관이냐면,

• eigenvector, eigenvalue를 찾는다는게 주어진 임의의 벡터를 transformation 했을 때 수 많은 벡터가 나올 수 있을텐데, 이 때 원래의 벡터와 방향은 같고, 크기만 변하는 벡터를 찾는 것과 같은 말이기 때문이다.
• 이게 어떤 의미인지 시각적으로는 여기에서 아주 잘 볼 수 있다.
  
  

# Eigenvector / Eigenvalue

고유벡터, 고유값이라고 부르는 이것은 늘 같이 다니는, 떨어질 수 없는 개념이다. (eigenvector가 있으면 eigenvalue가 반드시 있다는 말이다)

이 두 개념은 PCA의 근간을 다루고 있다는 것을 기억하고 다음을 보면 더 좋을 것 같다.

Eigenvector

위에서 말한 것처럼 Eigenvector란, 주어진 임의의 벡터를 transformation 했을 때 나오는 수 많은 벡터 중 원래 벡터와 방향은 같고, 크기만 변하는 벡터를 말한다.

• (위에서 이미지 링크 걸어둔 시각화 꼭 보자. 꼭!)

Eigenvalue

• 이렇게 원래의 벡터와 방향이 같고, 크기만 변한다는 의미는, 원래 벡터에 스칼라가 곱해진다는 것이다. 여기서 그 스칼라를 Eigenvalue라고 생각하면 된다.
• 다른 말로 하면 변화한 크기의 값이다.

이제 왜 이 두 개념이 같이 다니는지 이해가 갈 것이다.

이게 PCA랑 뭔 상관이야?

반드시 기억해야할 말이 하나 있다. 그건 바로 데이터의 분산이 클수록 데이터의 정보를 더 잘 유지한다는 것이다.

무슨 말? PCA에 대해 다룬 영상 중 찰떡 비유가 있었다.
만약 내 친구들이 한 10명 정도 옹기 종기 모여있고, 나는 카메라를 들고 걔네를 찍으려고 한다. 이때 나의 목표는 최대한 많은 친구들이 사진 속에 담기는 것이 될거다.

• 이때 좌우로 쓱 쓱 왔다 갔다 하면서 친구들끼리 최대한 겹치지 않는 지점을 찾을 것이다.
• 만약 친구들이 겹쳐서 누구 하나가 안 보인다면? 그 데이터는 유실된 것이다.
• 그렇게 사진을 찍으면, 3차원의 공간이 2차원의 사진으로 차원축소가 되는데, 이때 최대한 모든 친구들이 나오는 그 사진이 차원 축소를 할 때 가장 정보를 잘 보존했다고 할 수 있는 것이다.

이 분산이 가장 큰 지점이 바로 고유벡터이다

• 왜냐고? 자, 여기 시각화 자료! (출처는 링크 내 포함)

# 고차원의 문제 (The Curse of Dimensionality)

자, 차원 축소니, 데이터의 정보를 가장 잘 보존하느니 여러 얘기를 후다닥 했다. 그럼 왜 우리는 차원 축소를 하는지 말해볼 차례이다.

여기서 차원이란 Feature, 변수다. 만약 우리가 다뤄야할 변수가 1-2개가 아니라 200개나 된다면?

• 그럼 200차원인데, 이걸 공간적으로 우리가 생각할 수 있을까?
• 그 많은 데이터를 다 계산하는데 컴퓨터가 버텨줄까?
• 그것들 모두가 과연 우리가 '좋은 예측'을 하는데 도움이 될까?

당연히 아니다. 이렇게 고차원 데이터를 다룰 때의 문제점을 보자.

1. 시각화하기 어렵다.
   • 우린 데이터를 한눈에 파악하기 위해 다양한 시각화를 한다. 1차원은 선, 2차원은 평면, 3차원은 공간까지 우린 안다. 근데 만약 200차원이라면? 이걸 시각화를 어떻게 할 것이며, 우린 그걸 어떻게 이해할 수 있겠나?
2. 비효율성
   • 일단 데이터의 양이 많을 수록 우리는 정말 많은 리소스를 사용하게 된다. 일단 컴퓨터가 계산하는데 오래 걸리고, 오래 걸리면 프로젝트 데드라인을 못 지키고, 그러면 우리는 혼나고 ... 😂
   • 또 만약 10개의 피쳐가 있다고 해서 그 10개가 전부 필요할까? 만약 데이터의 일부를 제한하더라도 전체적인 의미(인사이트) 파악에 큰 차이가 없는 상황이라면 굳이 다 쓰지 않는 것이 더 나을 것이다.
3. Overfitting(과적합) 이슈
   • 훈련 데이터에 대해서 과하게 학습하여, 그에 대해서는 오차가 감소하지만, 실제 데이터에 대해서는 오차가 증가하는 문제를 말한다.

이러한 문제점들이 우리가 차원 축소를 하는 이유가 된다.

# Dimension Reduction

차원 축소를 하는 이유에 대해서는 알아봤고, 이제 그 종류를 알아보자. 크게 두 가지로 나뉜다.

1. Feature Selection
   • 분석 목적에 적합한 소수의 feature를 선택하는 것이다.
   • 즉, 기존의 데이터를 변형하지 않고 그대로 가져온다.
   • 그렇다보니 우리가 그 숫자를 보고 해석하기가 용이하다는 장점이 있다. 단, 소수만 선택하는 만큼 정보의 손실의 정도가 상대적으로 큰 단점이 있다.
2. Feature Extraction
   • 둘 이상의 변수를 조합하여 사용한다.
   • 즉, 기존의 데이터가 변형된 형태로 나타난다.
   • 장점으로는 feature들 간의 연관성이 고려되고(아무거나 합치지는 않을거니까), feature의 수를 많이 줄일 수 있다. 여러 피쳐들을 가져다가 합쳐서 쓰는 것이니 정보의 손실의 정도를 상대적으로 줄일 수도 있다.
   • 단점으로는 나온 숫자를 딱 보고 바로 해석하기가 어렵다. (무슨 말인지는 CPA 실습 예시에서 알게 될 것이다)

# PCA

주성분 분석(Principle Components Analysis).
PCA는 차원 축소를 하기 위한 기법 중 Feature Extraction의 한 종류이다.

즉, 고차원 데이터를 효과적으로 분석하기 위해 차원을 축소하여, 더 효과적인 시각화, Clustering이 가능하도록 해준다.

그럼 두 개의 변수가 담고 있는 정보를 '최대한 손실하지 않고' 하나의 차원으로 축소할 수 있을까? 뭘 기준으로 해야한단 말인가?

아까 데이터의 분산이 클수록 정보를 더 잘 유지한다고 말했었다. 이때 나오는게 앞서 말한 eigenvector, eigenvalue이다.


고차원 데이터의 정보(분산)을 최대한 유지하는 벡터를 찾고, 해당 벡터에 대해 데이터를 Projection하는 것이 바로 PCA라고 할 수 있다.

• (2차원을 1차원으로 축소하는 것에 대한 시각화는 앞서 언급한 여기 시각화 이미지를 다시 한번 보자)
• Eigenvalue는 feature의 수만큼 있지만, 그 중에서 Eigenvalue가 가장 큰 값을 골라서 하는 것이라고 생각하자.
• 참고로 PC1이 가장 분산이 크고 PC2가 그 다음으로 크다. (그냥 그렇게 뽑아준다고 생각하면 된다) 그리고 PC1, PC2는 직교한다.
  
  

우선 개념적으로는 이 정도 기억하면 될 것 같다.

말로 더 설명하는 것보다는 파이썬에서 어떻게 하는지, 결과는 어떻게 나오고 어떻게 해석할 수 있는지 한 번 보도록 하자.
(아래는 직접 적은 것이라 코드가 말끔하지는 않을 수 있다ㅠㅠ)

# 파이썬으로 실습을 해보자!

PCA 검색해보면 알겠지만, 굉장히 복잡한 수학적 계산 과정을 가지고 표준화하고 eigenvector 구하고.... 그러는 그럼 뭐야 내가 다 하나하나 풀어야 돼? 물론 아니다.

파이썬의 갓라이브러리 sklearn 을 사용하면 된다.

• (뭘 어떤 순서로 써야 하는지는 기억을 해야겠지만, 까먹어도 우리에는 갓구글이 있으니.. 그때의 나를 믿자..)
  
  

간단한 문제부터 시작해보자.

아래 matrix에 대해 numpy를 사용하여 고유벡터, 고유값을 구해보자.

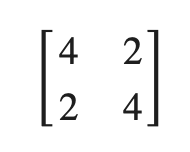
import numpy as np

#matrix 생성
data = np.array([[4,2], [2,4]])

#구하기
res = np.linalg.eig(data)

value = res[0]
vector = res[1]

print('value = ', value) 
print('vector = ',vector)

output

• 

참고로 value가 6과 2라는 건 원래 매트릭스를 선형 변환했을 때 크기만 바뀌고 방향은 바뀌지 않는 벡터가 원래 매트릭스의 6배, 2배라고 말할 수 있다.

PCA를 해보자.

seaborn에서 기본 제공하는 펭귄 데이터를 사요할 것이다. 4개의 feature(4차원)를 2차원으로 PCA할 것이고, PC1, PC2를 통해서 시각화까지 해보겠다.

#dataset 불러오기
import seaborn as sns
df = sns.load_dataset('penguins')
df = df[['bill_length_mm', 'bill_depth_mm', 'flipper_length_mm', 'body_mass_g']] 
#df.info() 를 통해 보니 결측치가 있음.

#결측치 처리 (의미 없는 값이니 제거해버렸는데 맞는지는 모르겠따.
df = df.dropna(axis = 0)
#2개 열이 제거되었다.

### 2차원으로 PCA ###
from sklearn.preprocessing import StandardScaler, Normalizer
from sklearn.decomposition import PCA

#데이터 표준화
scaler = StandardScaler() 
Z = scaler.fit_transform(df)

#축소하고자 하는 dimension 지정 
pca = PCA(2)
pca.fit(Z)

#고유벡터, 고유값 확인
print("\n Eigenvectors: \n", pca.components_)
print("\n Eigenvalues: \n",pca.explained_variance_)

#고유 벡터에 projection
B = pca.transform(Z) #시각화에 쓸 데이터

#Eigenvalues ratio
ratio = pca.explained_variance_ratio_
print("\n explained variance ratio: \n", ratio) #두 ratio를 합해보면 2개 PC를 사용했을 때 원래 데이터의 약 13% 정도가 loss가 일어난다. 

output

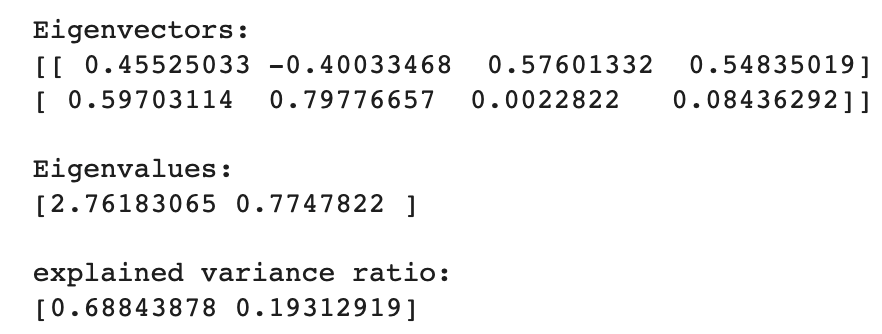
이 과정에 대해서 설명을 남겨놔야겠다.

• 먼저 데이터 표준화라고 하는 건, 각기 다른 스케일의 데이터를 영점으로 땡겨서 맞춰주는 것이다. 무조건 해야하는지는 모르겠지만, 다른 예시를 찾아보면 대부분 해주었던 것 같으니 일단 하는 걸로 기억하자.
• 2차원으로 축소했으니 Eigenvector는 가장 적합한 2개 값만 나온 걸 볼 수 있다.
• Eigenvalues ratio에 대해서는 주석을 보면 되지만, 첨언한다.
  - 모든 variance ratio의 합은 1이다. 만약 1이 아니라면 주성분 일부가 선택되지 않은 것이다. (ratio가 높은 주성분 일부만 선택한 것이다) 그러면 1-(비율)만큼의 정보가 손실되었다고 볼 수 있다.
  
  

시각화

#### species 정보를 담은 dataframe 생성####

# species only DataFrame 
df2 = sns.load_dataset('penguins')
df2 = df2[['species', 'bill_length_mm', 'bill_depth_mm', 'flipper_length_mm', 'body_mass_g']]
df2 = df2.dropna(axis = 0)
df2 = df2[['species']].reset_index() #똑같이 342 row에 대한 datafrmae을 가져옴.

# 'B' array -> DataFrame
import pandas as pd
B_df = pd.DataFrame(B, columns = ['PC1', 'PC2'])
B_df

# species + B
final_df = pd.concat([df2, B_df], axis = 1)

### Visualization ### 
sns.scatterplot(data =final_df, x = 'PC1', y = 'PC2', hue = 'species')

output
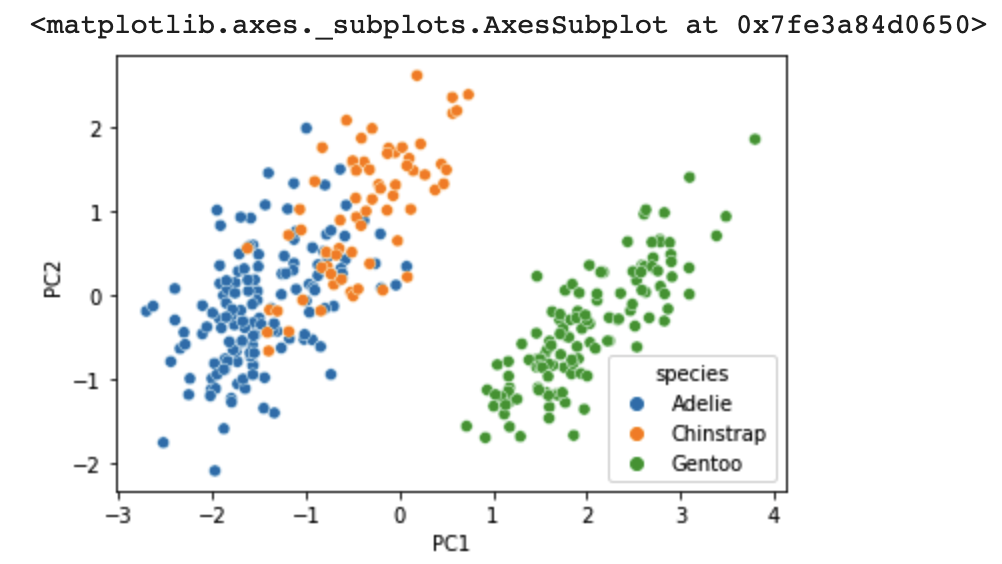나는 아예 새롭게 데이터프레임을 만들어서 시각화했는데, 다른 더 좋은 방법이 있는지는 모르겠다.