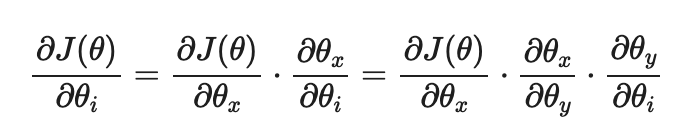220704_TIL / training Neural Network

신두다·2022년 7월 4일

목록 보기

51/82

Key words

순전파(Forward propagation / Feedforward), 역전파(Backpropagation), 손실함수(Loss function), 옵티마이저(optimizer), 경사하강법(Gradient Descent), 확률적 경사하강법 (Stochastic GD), Mini-batch GD

1. 신경망은 어떻게 학습이 이루어질까?

[반드시 기억하기!]
1. 데이터가 입력되면 신경망 각 층에서 가중치 및 활성화 함수 연산을 반복적으로 수행한다.
2. 1의 과정을 모든 층에서 반복한 후에 출력층에서 계산된 값을 출력한다.
3. 손실 함수를 사용하여 예측값(Prediction)과 실제값(Target)의 차이를 계산한다.
4. 경사하강법과 역전파를 통해서 각 가중치를 갱신한다.
5. 학습 중지 기준을 만족할 때까지 1-4의 과정을 반복한다.

순전파란 입력층에서 입력된 신호가 은닉층의 연산을 거쳐 출력층에서 값을 내보내는 과정을 말한다.

쉽게 input layer로 값이 들어간 후 가중치-편향 연산을 거쳐 활성화 함수를 통해 다음 layer로 전달되는 과정을 생각하면 된다.

손실함수(Loss Function)

이렇게 한번 output layer를 거치면 어떤 예측값이 튀어나올텐데, 여기서 우리가 이런 모델링을 하는 목표는 뭐다?! 실제값과 예측값의 차이를 줄이는거다~!
이때 쓰이는게 바로 손실함수다. 출력된 예측값과 실제값(=타겟값)은 이 손실함수에 들어가 손실(loss/error)을 계산하게 된다.
대표적인 손실함수로는 MSE(Mean-Squared Error), CEE(Cross-Entropy Error)가 있다. (이것에 대해선 머신러닝 할 때 다뤘기 때문에 낯선 개념은 아니다.)
- 다중분류 문제에서 사용할 수 있는 손실함수로 categorical_crossentropy / spase_categorical_crossentropy
  가 있는데, 이 둘의 차이는 이 글을 참고하자.

역전파 오늘의 핵심..!!!

역전파는 말 그대로 순전파의 반대말이다. 순전파가 input layer > output layer 방향으로 진행되었다면, 역전파는 손실 정보(예측값과 타겟값의 차이)를 output layer > input layer까지 전달하며 각 가중치를 얼마나 업데이트 해야할지를 구하는 알고리즘이다.
이때 가중치 업데이트는 손실(Loss)를 줄이는 방향으로 진행된다. 당연하겠지!
근데 이때 가중치를 어떻게 수정해야 손실을 줄일 수 있을까? 바로 그 때 쓰는 게 경사하강법(Gradient Descent, GD)이다.

경사 하강법

이 수식은 기억해두어야 한다.
경사 하강법은 머신러닝할 때 한 번 봤었다. 매 iteration (= 순전파 역전파 한번 도는 것)마다 해당 가중치에서의 비용함수의 도함수를 계산해서 경사가 작아질 수 있도록 가중치를 변경하는 것이다.
- (만약 나중에 너 이 말 다시 보고 헷갈리면 경사하강법에서 비용함수를 미분한 값이 0에 가까워지도록 하는 것이 오류(손실)를 최소화하는 것이라는 의미를 까먹은거니까 다시 공부하거라)

여기서! 옵티마이저(Optimizer)를 한 번 얘기해보자.

옵티마이저는 쉽게 말해 경사를 내려가는 방법을 결정하는 것이다. 이런 것들이 있는데, 다 외우지는 않아도 된다고 함.
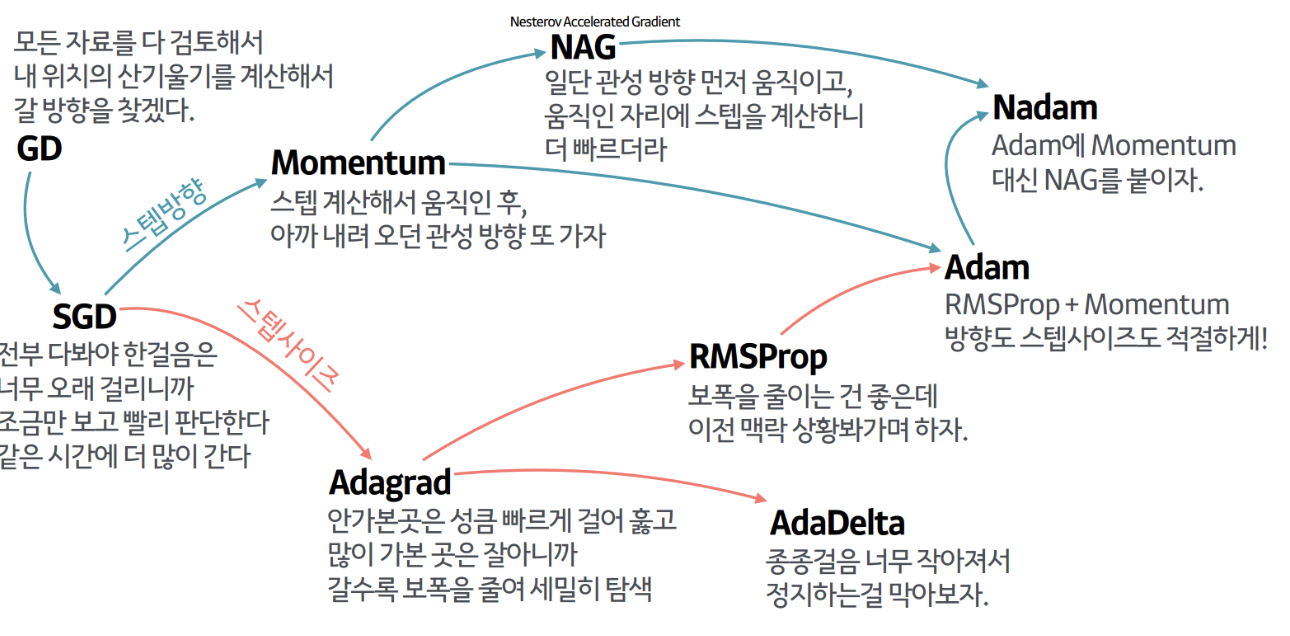
우리가 일반적으로 쓰던 경사하강법은 위 이미지에서 GD이다. 한 iteration마다 주어진 모든 데이터를 다 쓰면서 가중치를 업데이트 하는거다. 그럼 문제가 뭐다? 데이터가 많으면 시간이 엄청나게 들겠지!
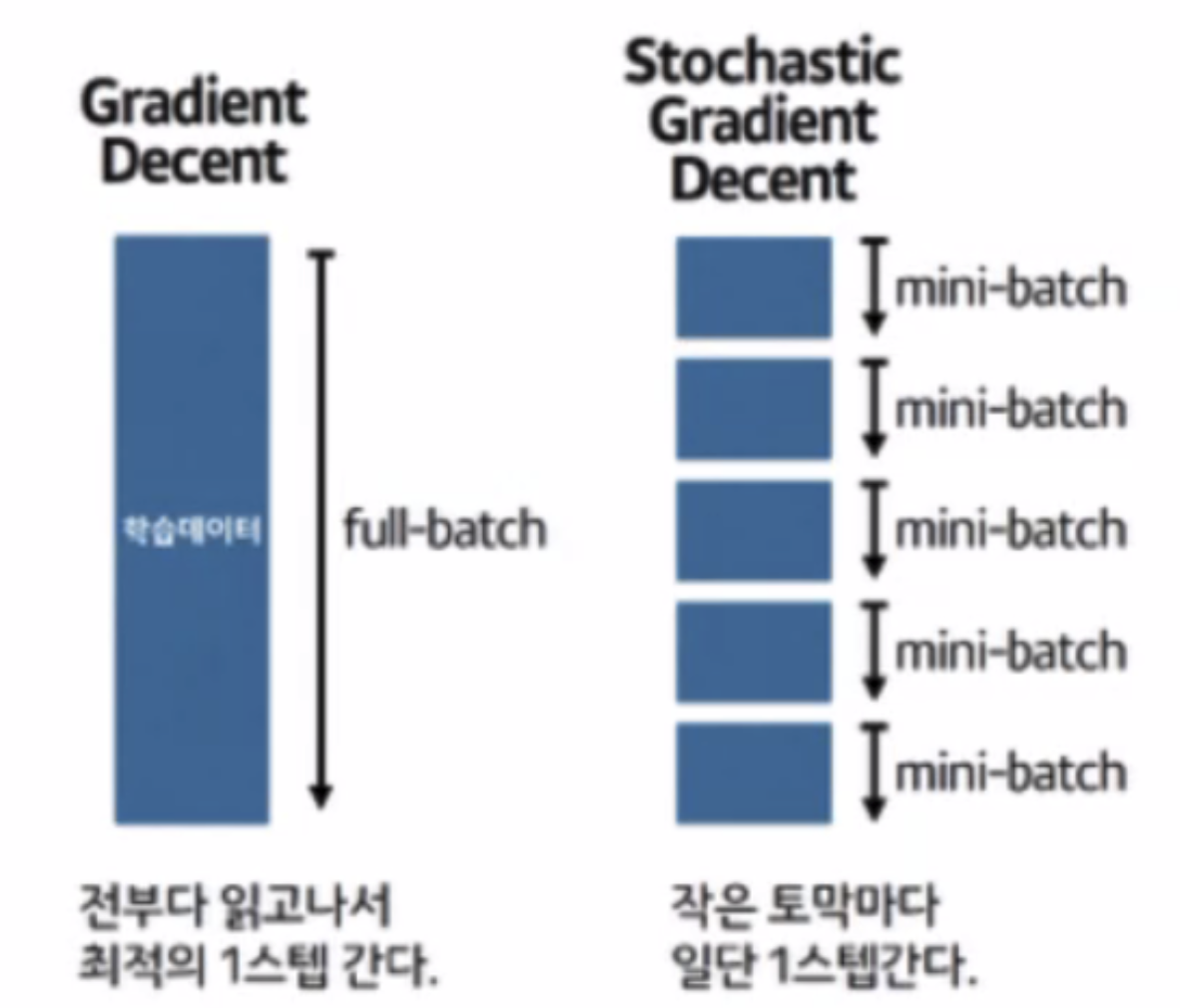
그래서 이 문제를 해결하려고 나온게 바로 확률적 경사하강법(SGD)과 mini-batch 경사하강법이다.
- 먼저 확률적 경사하강법(SGD). 이건 전체 데이터에서 딱 하나의 데이터를 뽑아서 신경망에 입력한 후 손실을 계산하고, 그 정보를 역전파하여 가중치를 업데이트 하는 방법이다. 다시 말해 한 iteration 마다 1개의 데이터를 사용한다는 거다.
  - 하나씩 돌리니 가중치를 빠르게 업데이트할 수 있다는 장점은 있지만, 만약 그 1개의 데이터가 Outliar라면? 학습과정에서 불안정한 경사하강을 보일 수 있는 단점이 있다. (여기저기 쓕쓕 튈 수도 있을거 같다.)
- 이런 SGD의 문제점을 개선하고자 나온게 바로 mini-batch 경사하강법이다. 아까 SGD가 딱 1개의 데이터만 썼다면, 미니배치 경사하강법은 지정된 N개의 데이터를 쓴다는 차이만 있다. 이때 이 N개는 batch size 라고 부른다.
  - 참고1. 메모리 크기가 허락한다면 큰 배치 사이즈를 쓰는 것이 학습을 안정적으로 진행할 수 있다고 한다. SGD가 이상치 때문에 튈 수 있던 상황을 생각하면 될 듯.
  - 참고2. 만약 총 데이터 1000개에서 배치 사이즈를 256개로 하면, 마지막에 배치에서 232개 밖에 없는데 이때는 어떻게 할까? 정답은 그냥 232개로 돌려서 가중치를 갱신한다고 한다.

잠깐 여기서 나중에 헷갈릴 것 같은 것 정리하고 가보자.

Q. 아래 조건에 따라 학습을 진행할 경우 전체 Iteration 횟수로 알맞은 걸 골라주세요.

조건1) 학습에는 총 20000개의 데이터를 사용한다.
조건2) Batch size는 1000, Epoch는 5로 설정한다.

정답은?! 100이다.
--
- Epoch란 데이터셋 전체를 이용해서 학습한 횟수를 말한다.
- 즉, 한 epoch에는 20000/1000인 20번의 iteration이 돌게 되고, 이걸 5번 반복하면 총 100번의 iteration이 도는거다.

(참고로 iteration은 무조건 전에 골랐던 데이터를 제외한 나머지 중에 선택된다고 한다.)

당연하게도 어떤 옵티마이저가 가장 좋은지 정답은 없고 사바사라고 한다. (근데 잘 모르겠으면 일단 adam을 써보면 된다고 한다. 성능이 꽤 잘 나온다고 함.)

자, 여기까지 하면 우리가 케라스 돌릴 때 쓰던 model.compile의 각 요소에 대해서 공부한 것이다.

model.compile(optimizer='adam',
              loss='sparse_categorical_crossentropy',
              metrics=['accuracy'])

2. 역전파 편미분 / Chain Rule(연쇄 법칙)

아, 역전파 편미분해서 가중치 찾아나가는거 오늘 여럿 봤는데 정말 이해하기 너무 힘들었다. 이 웜업영상도 그렇고.. 무조건 알아야 하는건데,,!!!
이 영상도 추가로 찾아봤었음.
일단 오늘은 시간이 늦었으니까 주말에라도 시간내서 다시 공부하자.

Chain Rule은 이전에 함수 속에 또 함수가 있을 때 겉미분*속미분이걸로 기억하고 있었다. 오늘은 특정 변수에 대한 (편)미분 값을 다른 변수의 미분을 사용하여 나타낼 수 있는 방식으로 보았다.

3. 퀴즈 푼 것

퀴즈 푼 것중 코드와 관련해서 기억해야할 것만 옮겨둔다.

1. 빈칸에 들어갈 숫자를 모두 더한 값은?

은닉층은 총 __개다.
입력층에서 은닉층으로 갈 때의 가중치는 __개다.

from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense

model = Sequential()
model.add(Dense(5, activation='relu', input_dim=2))
model.add(Dense(3, activation='softmax'))

정답은 11이다. 이거는 가중치 행렬에 대한 것이다. 은닉층이 1개인 건 쉽게 알 수 있을거고. 입력층의 노드는 2개(input_dim)이고 은닉층에 노드가 5개 있으니 10개의 가중치가 존재하는 거다.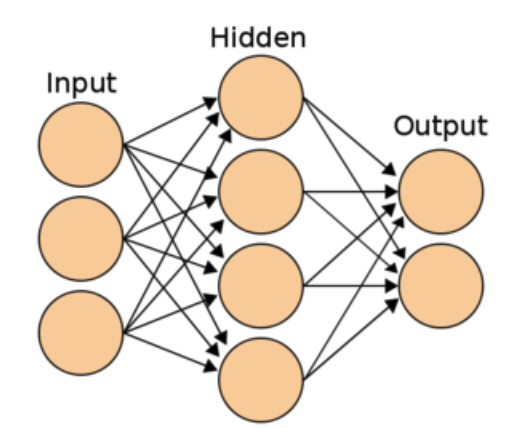

근데 그러면 여기서 또 헷갈리는 문제가 하나 있었다.
바로 model.summary()를 했을 때 나오는 pram(파라미터의 수)를 구하라는 거였다.

여기서 파라미터는 입력노드와 출력노드에 대해 연결된 간선의 수를 말한다. 즉 위위 이미지에서 저 각 노드간 연결되어있는 선들!을 말한다.
그럼 만약 1번 문제에서 입력층 > 은닉층의 파라미터의 수를 구하면 10일까? 아니다. 정답은 12다. 왜냐? 인풋에 편향(instance, bias) 노드가 추가되기 때문이다.
근데 이게 input layer > hidden layer로 넘어갈 때 뿐 아니라 그 이후 Layer이동할 때도 편향이 계산되길래, 이게 참 헷갈려서 아래와 같은 질문을 하기도 했다.

(...) 제가 드린 질문의 포인트는 은닉층에도 편향이 있다는게 어떤 의미인지였습니다. 금요일에 본 신경망 그림에서는 instance가 input layer에서만 표시가 되어있던 것 같거든요. 근데 레이어 넘어가면서 파람 구하는거 보면 매 레이어마다 편향이 있다는 것처럼 여기는데 그 의미가 뭔지 궁금했어요)
대답은 모든 노드에는 편향이 존재하며, use_bias 파라미터의 디폴트가 True여서 모든 은닉층에서도 편향을 포함해 계산한다고 한다. 만약 use_bias 파라미터를 False로 하면 미포함 계산 가능였다.
이 사이트 참고했고, 암튼 가중치 행렬이랑은 헷갈리지 말자!!!

4. 실습한 것

[sigmoid 함수 구현하기]
$S(x) = (1+e^-x)^-1$

class Sigmoid:
    def __init__(self):
        self.out = None

    def forward(self, x):
        out = 1 / (1 + np.exp(-x)) # 위의 sigmoid 식을 그대로 표현하면 된다. 
        self.out = out
        return out

    def backward(self, dout):
        # dout : 앞선 레이어에서 chain rule에 의해 넘어온 값
        dx = dout * (self.out * (1-self.out)) # sigmoid(x)를 x에 대해 미분하면 sigmoid(x)(1-sigmoid(x))이다. 
        
# 레퍼런스 http://taewan.kim/post/sigmoid_diff/ & https://wiserloner.tistory.com/m/1076

이건 Sigmoid 함수가 뭔지, 미분하면 어떻게 되는지를 알면 풀 수 있는 문제였다.
참고로 sigmoid 함수 미분은 증명 보고 나도 아래와 같이 따라해보았다.
역전파 노트별 정리 부분의 이 블로그 글도 좋았다. 참고하자.

[softmax 구현하기]

def softmax(x):
    return np.exp(x) / np.sum(np.exp(x)) # 증명은 나중에 해보자.

test_array = np.array([19, 15.5, 10.4, 3.33, 20.8])

# tensorflow softmax와 값 비교
print(softmax(test_array)) # 결과 해석: 각각의 클래스에 속할 확률을 나타내준다. 합은 1이며, 그 중 가장 확률이 가장 큰 클래스에 속한다고 결론을 내릴 수 있음.  
print(tf.nn.softmax(test_array))

레퍼런스
나중에 증명 해보자.. softmax 수식 찾아서 표현만 해봤다.

[cross_entropy 구현하기]

def cross_entropy_loss(y_true, y_pred):
    first = y_true*np.log(y_pred + (1e-7)) # 레퍼런스: 디스코드에 공유된 수식 & https://kejdev.tistory.com/41
    second = -np.sum(first)
    return second

참고하자.

[Keras 이용하기]

32개의 노드를 가진 입력층, 64개, 256개의 노드를 가진 각 1개(=총 2개)의 은닉층, 5개의 클래스로 구성된 데이터를 가진 신경망을 만들고자 합니다. 주석 처리된 곳에 알맞은 숫자를 입력해주세요.

from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense

A = 64
B = 32
C = 256
D = 5

model = Sequential([
    Dense(A, activation='sigmoid', input_dim=B), # A, B
    Dense(C, activation='sigmoid'), # C
    Dense(D, activation='softmax') # D
])

lossFunction = 'categorical_crossentropy' # activation function으로 softmax가 쓰였으니 다중 분류 문제임. sparse_categorical_crossentropy도 가능
batch_size = 50 # 1-3번 문제의 조건을 보고 지정해둠.

model.compile(optimizer='sgd', loss=lossFunction, metrics=['acc'])
 
results = model.fit(X,y, batch_size=batch_size, epochs=100)

진짜 이거 헷갈리기 딱 좋을 듯!!!!!!! 잘 기억해둬라.

5. 그 외

지수함수는 미분해도 자기 자신이다. 다시 찾아봤음..

Feeling

오전부터 역전파 편미분 때문에 완전 멘붕의 연속이었다. 오늘은 수학적 개념을 가장 많이 다뤘던 것 같다. 아~ 수학이시여~~ 그래도 그 전에 자의건 타의건 공부 안 해서 이번에 처음 본 거니까 혼나면서 배워야지 뭐 어쩔 수 있나!
그래도 오늘 sigmoid 미분 증명 따라해보며 이해한거는 재밌었다. 어차피 수학은 언젠가라도 반드시 다시 만나서 해야할 공부니까 재미있게 해보자!

신두다

B2B SaaS 회사에서 Data Analyst로 일하고 있습니다.

이전 포스트

220701_TIL / Neural Networks (딥러닝 섹션 시작!)

다음 포스트