220705_TIL / Learning rate, Weight Initialization & Regularization

신두다·2022년 7월 5일

TIL

목록 보기

52/82

Key words

학습률, 학습률 감소 / 계획법, 가중치 초기화, 과적합 방지 기법(가중치 감소, 드롭아웃, 조기종료)

오늘 배운 것은 신경망 학습이 더 잘되도록 하는 방법에 대한 것이다. 이 점을 기억하며 다음 내용을 읽어보면 된다.

Overview - 학습이란?

(오전 QnA 세션 때 설명들은 내용인데 좋았어서 적어둔다.)

꼭 머신러닝을 한다고 안해도 학습이란게 뭔지 정확히 설명할 줄 알아야 한다. 아래 그림을 보자.
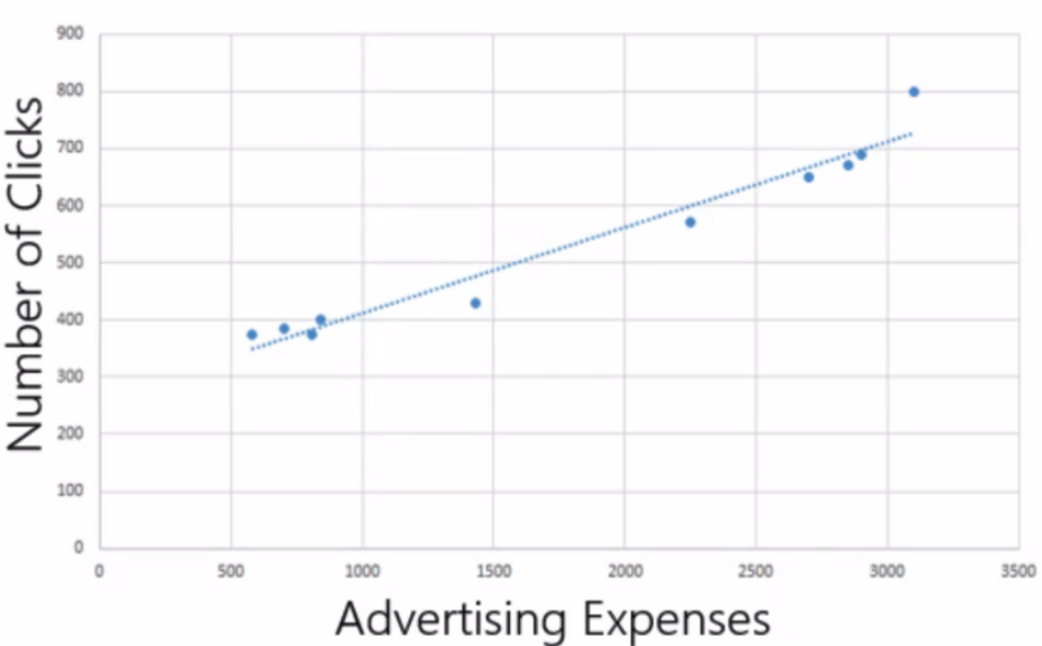
$y=ax+b$ 1차 함수가 있다. 인공지능에서는 a를 가중치, b를 편향이라고 한다.
우리가 예측해야 하는 y는 클릭수. x는 광고비인데 여기서 x는 바꿀 수 없다. (가지고 있는 데이터를 조작할 수는 없잖아!!) 대신 우리는 a,b를 바꿀 수 있다.
그럼 예측값과 실제값의 차이가 적은 식을 만들기 위해, 맨 처음에는 a,b를 랜덤하게 찍고 시작할 수 밖에 없었는데, 하다보니까 아 완전 랜덤하게 하는 것보다는 어느 규칙들이 있네?? 라고 해서 나온게 바로 가중치 초기화의 방법들이다.
그 후 가중치와 편향을 더 나은 값으로 업데이트하면서 예측값을 잘 맞추는 과정을 ‘학습'이라고 한다.
그럼 가중치와 편향을 한 번 갱신했다. 근데 한 번으로 완벽할까? 완벽한 가중치와 편향값을 찾을 수 있을까? 운이 좋다면 할 수는 있겠지만 대부분은 아니다. 그럼 값을 업데이트 해야할 거 아니야~ 그럼 이 값을 어느 정도의 크기로 업데이트 해야할까? 이걸 누가 관장하나? 바로 오늘 배운 학습률이다.

1. 학습률이란?

학습률 Learning rate이란 매 가중치에 대해 구해진 기울기 값을 얼마나 경사 하강법에 적용할지를 결정하는 하이퍼 파라미터이다.
- (잠깐, 하이퍼 파라미터는 뭐다? 연구자가 설정하는거다)
어제 보았던 이 그림이 여기서 다시 매우 중요해진다.
위 정의는 솔직히 너무 어려운데, 쉽게 말해 경사하강법이 예측값과 실제값의 에러를 줄이기 위한 비용함수의 미니멈을 향해 산길을 내려가는 과정이라면, 학습률은 얼마나 이동할지 그 보폭을 결정하는 거라고 생각하면 된다.

근데 오늘 이 내용 공부하면서 경사하강법에서 학습률에 따라 그래프상으로 어떻게 작용하며 내려간다는거지? 그 부분이 문득 헷갈려서 다시 찾아서 공부했다. (참고영상)

경사하강법은 함수의 최솟값을 찾는 문제에서 이용된다. 함수가 너무 복잡해 미분 계수를 구하기 어려운 경우나 데이터의 양이 너무 많아 효율적인 계산이 필요하거나 하는 상황에서는 미분 계수를 구하는 것보다는 경사하강법을 사용하는 것이다. 여기까진 오케이.
내가 위 영상에서 도움을 받았던 건 경사하강법의 수식 유도 부분이었다. 이걸 이해하고 나니 위 그림의 식도 잘 이해할 수 있었다. 이어서 한번 정리해보겠다. (그리고 이게 뒤에 나올 내용을 이해하는데도 아주 큰 도움이 된다)
경사하강법은 함수의 기울기(gradient)를 이용해 x의 값을 어디로 옮길 때 최솟값을 갖는지 알아보는 방법이다.
- 즉, 기울기가 양수인 경우 x의 값이 커질수록 함수의 값이 커지며, 기울기가 음수인 경우 x의 값이 커질수록 함수의 값이 작아진다.
그러면 함수의 값이 작아지는 방향으로 움직이려면 각각 어떻게 해야할까 생각해보자. (2차 함수를 딱 머릿속에 그려놓고 생각해봐!!)
- 기울기가 양수인 경우, x가 작아지는 방향으로 옮겨야되고 / 기울기가 음수인 경우 x의 값이 커지는 방향으로 옮겨야겠지!!
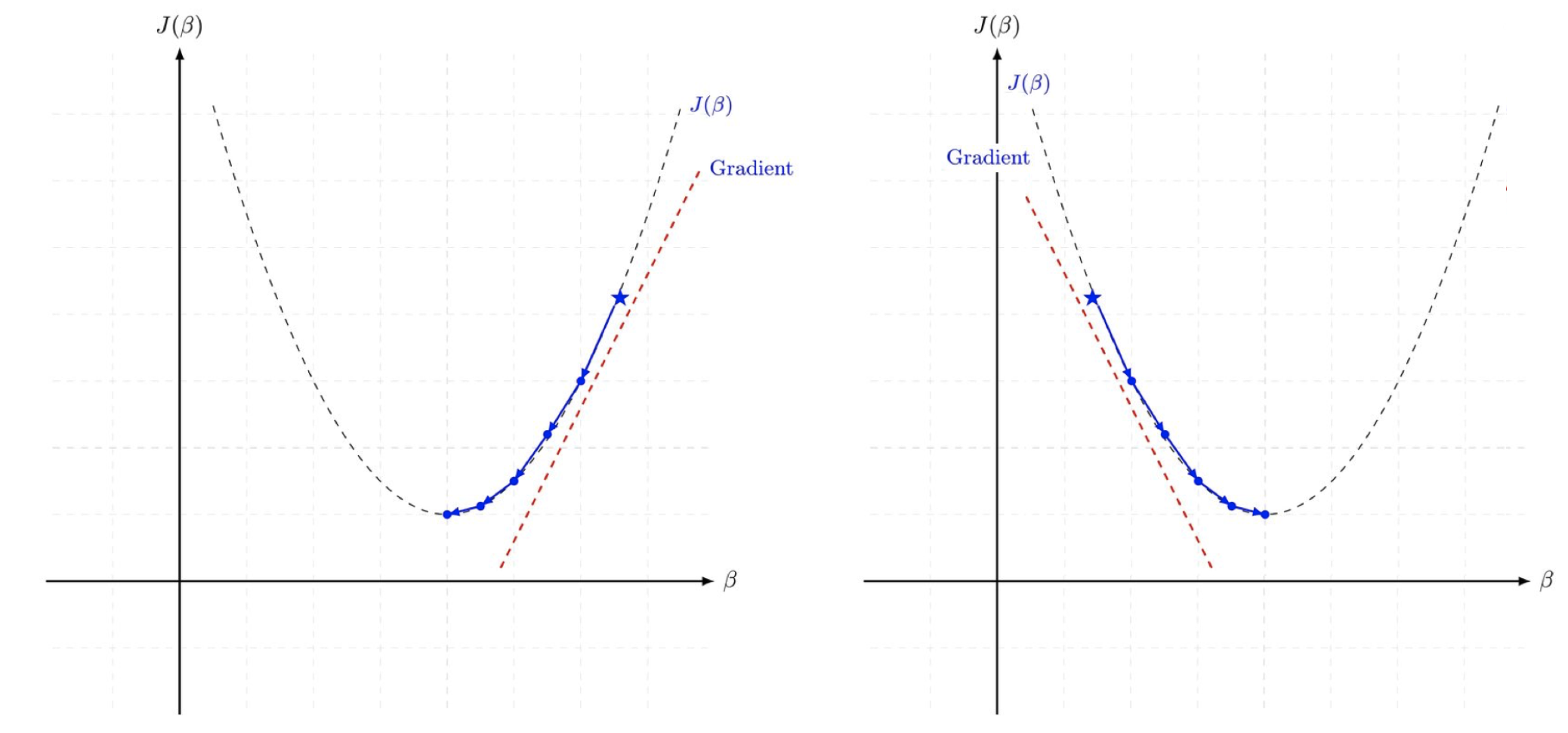
- 그래서 위 그림에서 기울기 반대 방향으로 이동이라고 하는거다. 그래서 기울기 앞에 -가 붙어있는 거고.
- 기울기의 크기는 그러면 최솟값에 가까워질수록 그 크기는 작아지게 되는거고, 따라서 최솟값에 가까울수록 조심히 움직여야 발산하지 않게 되는거다.
또 하나, 학습률에 대해서. 학습률은 사용자의 필요에 따라 이동거리를 조절할 수 있는 step size라고 생각하면 된다.
- 이따 3번에도 적어두겠지만 오늘 본 말 중에 학습률의 감소 주기는 100 step이다.라는 말이 있었는데, 만약 초기 학습률이 0.001이었다면 그 다음 학습률은 0.001*100으로 생각하면 됨.
다시 맨 위의 수식 그림을 다시 보자. 학습률이 보폭을 결정하는 거라고 했는데, 학습률이 엄청 크면 어쩌겠어? 기울기가 너무 크게 팍 줄어들면서 아래로 확~~ 가버리겠지? 그래서 적절한 학습률을 찾는게 중요하다.
말로 길게 썼는데, 위 영상을 글로 정리한 이 블로그 글에 가면 직접 gif도 돌려볼 수 있으니 경사하강법이 헷갈릴 땐 무조건 애용하도록 하자. 꼭!
(참고로 내가 빠진에 로컬 미니멈인지 글로벌 미니멈인지는 알 수 없다고 한다. 근데 로컬 미니멈에 빠졌을 때 아직 iteration이 남은 경우 옵티마이저를 활용해 글로벌 미니범으로 갈 수 있도록 관성을 타고 넘어갈 수도 있게 해준다고 함. 정확한 원리는 모르겠음)

아무튼 정리!
최적의 학습률을 설정하는 것이 매우 중요하다.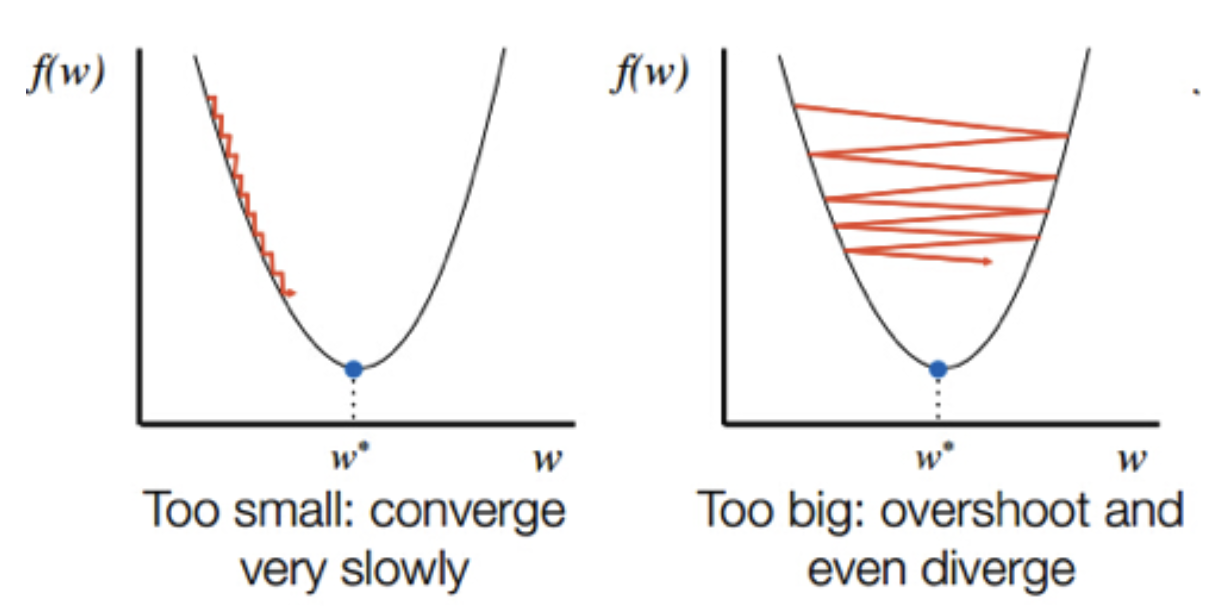

2. 학습률 감소/계획법

자, 1번을 통해 최적의 학습률을 찾는 것이 왜 중요한지는 알아보았다. 그러면 최적의 학습률은 어떻게 찾을 수 있을까? 그때 사용하는 것이 학습률 감소(Learning rate decay), 학습률 계획법(Learning rate scheduling)이다.

학습률 감소(Learning rate decay)

이미 adam 등의 주요 옵티마이저에 구현되어 있어 쉽게 적용할 수 있다고 한다.

model.compile(optimizer=tf.keras.optimizers.Adam(lr=0.001, beta_1 = 0.89)
             , loss='sparse_categorical_crossentropy'
             , metrics=['accuracy'])

beta_1이 뭔지는 나중에 쓸 때 찾아보면 된다고 함!?

학습률 계획법(Learning rate scheduling)

이건 좀 이해하기 어려웠는데, 이 그림을 보자.
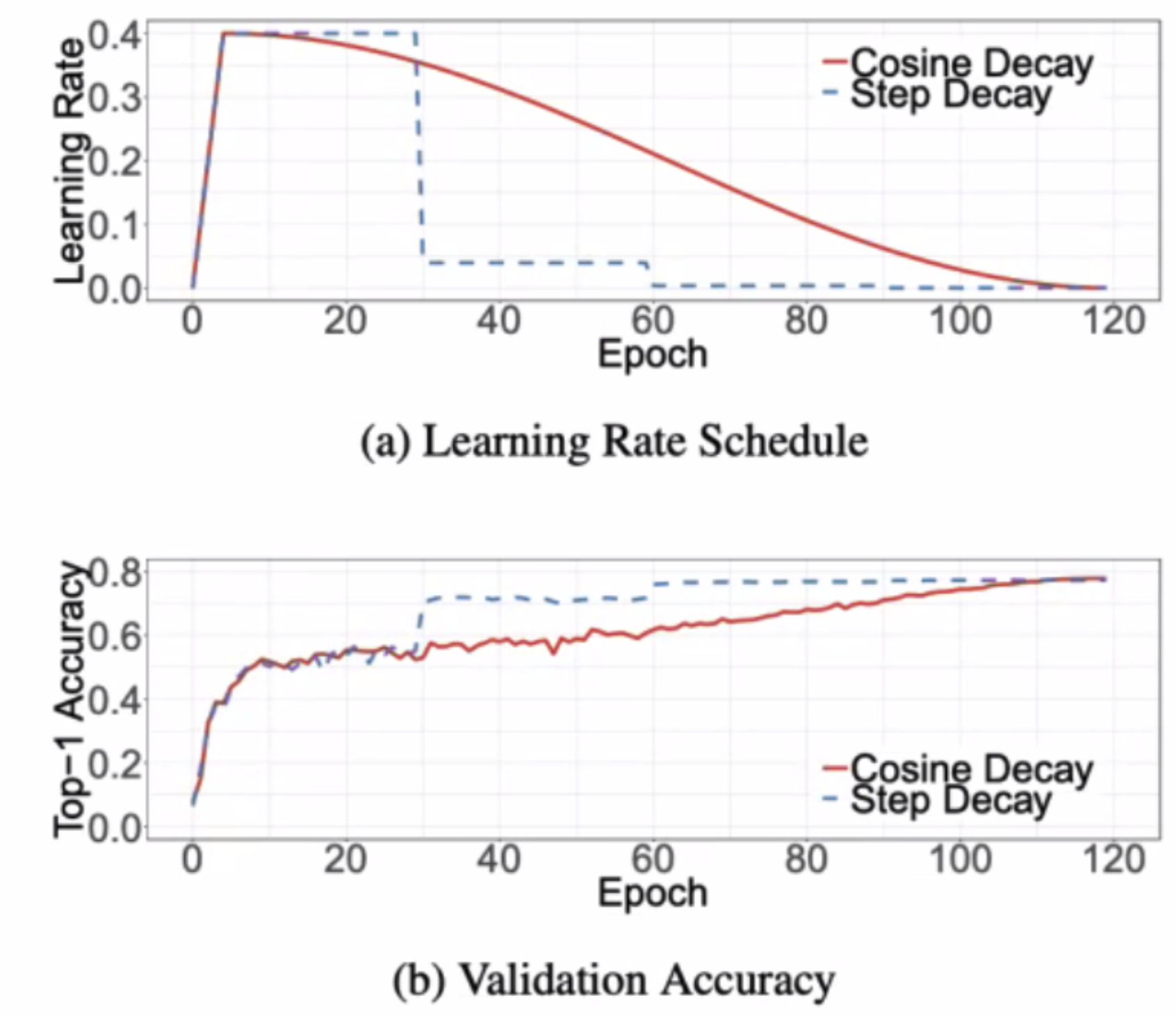
내가 이해한 걸로는 처음 warm-up step에서 학습률 보폭 크게 해서 정확도 빠르게 올리고, 어느 지점에서 다시 학습률 낮춰서 보폭 낮추고 조금씩 가면서 정확도를 점점 올려나가며 최적화된 상태를 찾는 것. (보폭이 계속 크면 뱅글뱅글 돌면서 글로벌 미니멈 찾기가 어려우니까)이었는데 맞는지는 찾아봐도 헷갈린다. 좀 더 찾아봐야할 듯.
- 오늘 찾아본 것 중 하나, 둘
코드로는 .experimental 내부 함수를 통해 설계 가능.

first_decay_steps = 1000
initial_learning_rate = 0.01
lr_decayed_fn = (
  tf.keras.experimental.CosineDecayRestarts(
      initial_learning_rate,
      first_decay_steps))  


 model.compile(optimizer=tf.keras.optimizers.Adam(learning_rate=lr_decayed_fn)
             , loss='sparse_categorical_crossentropy'
             , metrics=['accuracy'])

3. 가중치 초기화

가중치 초기화(Weight Initailization)는 신경망에서 매우 중요한 요소라고 한다. 근데 이름이 초기화라고 해서 헷갈렸는데 reset이 아니라 초기값을 잡아주는 거라고 생각하면 된다.
위 overview에 적어뒀던 것처럼 처음에 가중치를 아예 랜덤하게 찍고 시작하는 것보다는 어느 정도 효용이 있는 방법을 이용해 찍고 시작하는 것!
오늘 본 종류는 3개다. 수식을 외울 필요는 없고 어떤 초기화 방법이 있고 각각 언제 사용되는지만 알면 된다고 함.

1. 표준편차를 1인 정규분포로 가중치를 초기화 할 때 각 층의 활성화 값 분포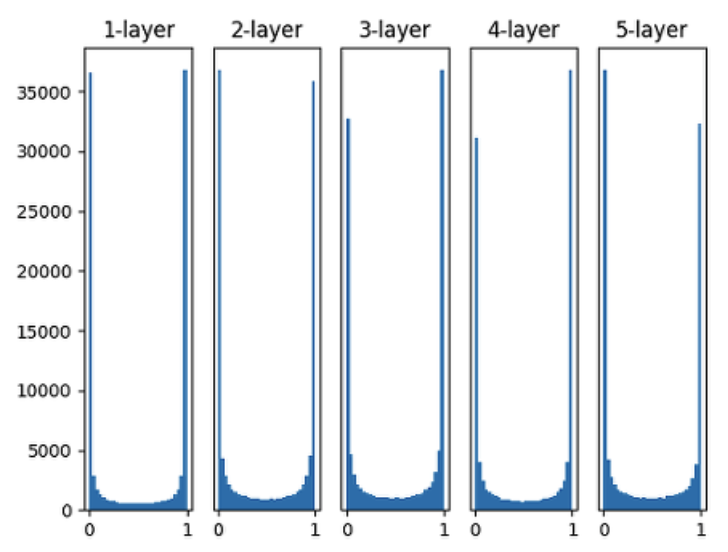

그래프에서 대부분 0, 1에 있는 걸로 봐선 활성함수로 sigmoid 함수가 쓰인 걸 알 수 있는데, 이렇게 되면 학습이 제대로 이루어지지 않는다. (왜 그런지는 이 글 참고)
그래서 가장 간단한 방법임에도 잘 사용되지 않는다고 한다.

2. Xavier 초기화를 해주었을 때의 활성화 값의 분포

1번의 문제를 해결하기 위해 나온 방법이다. (케라스에서 Xavier 초기화는 이전 층의 노드가 𝑛개이고 현재 층의 노드가 𝑚개일 때, 현재 층의 가중치를 표준편차가 $2/√(n+m)$ 인 정규분포로 초기화한다고 한다.)
케라스에선 glort_normal라고 한다. 만든사람이 glort xavier라서 그렇다.

3. He 초기화를 해주었을 때의 활성화 값의 분포

사비에르 초기화는 활성화 함수가 sigmoid인 신경망에서는 잘 작동하나 활성화 함수가 ReLu일 경우 층이 지날수록 활성값이 고르지 못하게 되는 문제를 보인다. 이런 문제를 해결하기 위해 등장한게 He initailization이다. He 초기화는 이전 층의 노드가 n개일 때, 현재 층의 가중치를 표준편차가 $2/$ √n인 정규분포로 초기화합니다.

요약!! Activation function에 따른 초기값 추천

Sigmoid / Softmax ⇒ Xavier 초기화를 사용하는 것이 유리
ReLU ⇒ He 초기화 사용하는 것이 유리

4. 과적합을 막기 위한 방법

딥러닝도 머신러닝의 하위 범주다보니 과적합 문제가 많이 일어난다고 한다. 더군다나 모델 복잡도가 훨~~~씬 더 복잡하니 그럴만도..
그럴 때 쓸 수 있는 방법들을 오늘은 3개 배워보았다.

1. 가중치 감소 (Weight Decay)

과적합은 주로 가중치가 클 때 발생하기 때문에 가중치가 너무 커지지 않도록 적절한 제약을 걸어주는거다. 머신러닝 초반에 배운 Ridge Regression을 생각하면 된다.
수식은 다음과 같다.
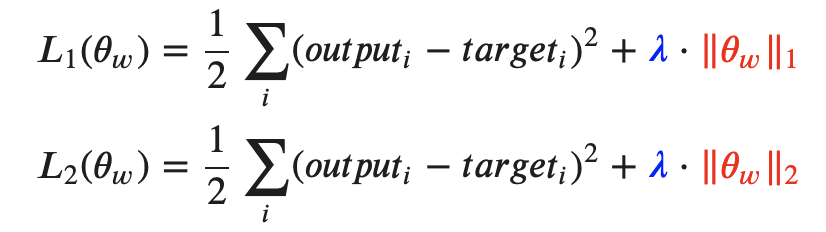
Keras에서는 다음과 같이 구현할 수 있다.

Dense(64,
      kernel_regularizer=regularizers.l2(0.01),
      activity_regularizer=regularizers.l1(0.01))
 
# `kernel_regularizer` ⇒ 가중치 제한해주는 것. 위 코드에서는 l1,l2 둘다 적용한 거임. 0.01은 람다값임.
# `activity_regularizer` ⇒ 출력값을 규제해준다.
# `bias_regularizer` ⇒ 편향을 규제해준다.

2. 드롭아웃 (Dropout)

Iteration마다 레이어 노드 중 일부를 사용하지 않으면서 학습을 진행하는 방법이다. 아래 그림을 보면 쉽게 이해가 갈 것이고, 이전에 배웠던 앙상블 모델 개념을 떠올리면 된다.
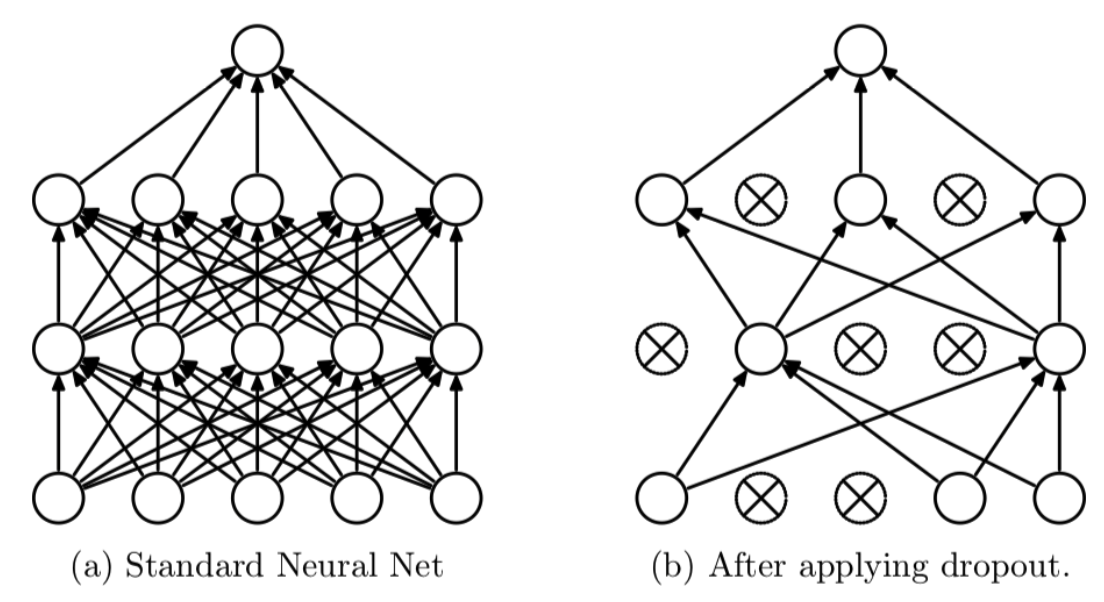
코드로는 다음과 같이 구현할 수 있다. 0~1 사이의 실수를 입력하는데 해당하는 비율만큼 드롭시키고 나머지만 사용하는 거다.

Dense(64,
      kernel_regularizer=regularizers.l2(0.01),
      activity_regularizer=regularizers.l1(0.01))
Dropout(0.5) # 50% 의 노드를 드롭하겠다는 뜻. 즉 32개만 쓰겠다.

3. 조기 종료 (early stopping)

섹션2 프로젝트 때 써봤던 건데 오늘 배우니까 정확히 끝나는 시점이 너무 헷갈렸어!! 여하간 개념은 이 그림 보면 이해 가능.
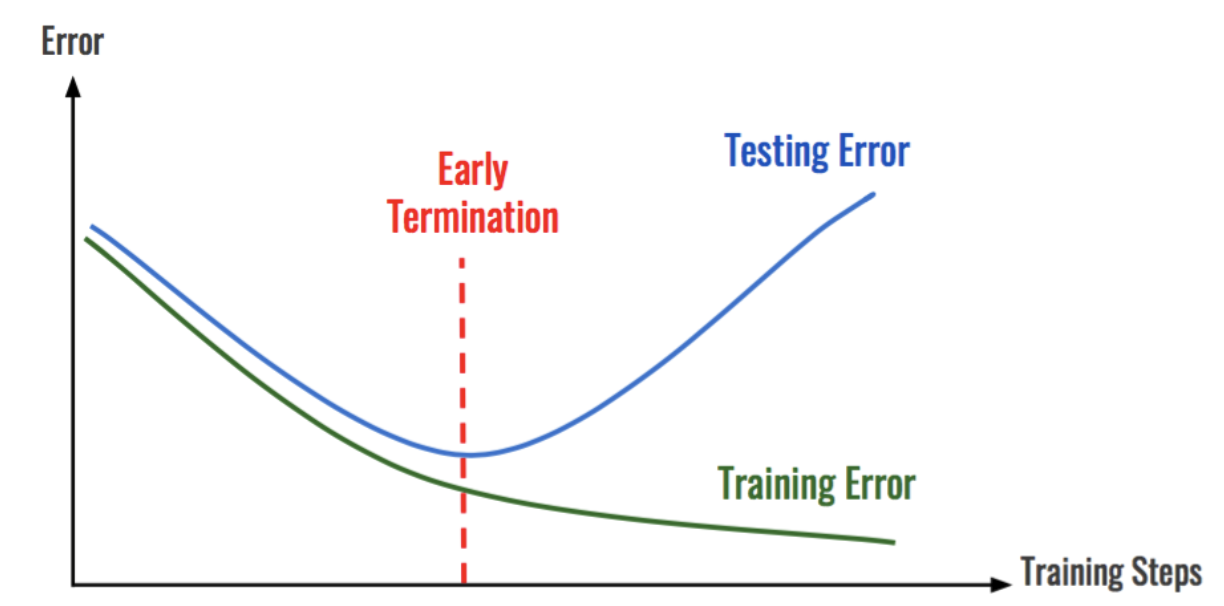
말로 풀어보면, 조기종료는 학습데이터에 대한 손실은 계속 줄어들지만, 검증 데이터에 대한 손실은 증가하는 경우 설정한 Epoch에 도달하기 전이라도 학습을 종료하는 방법이다.
이거 코드는 좀 길어서 어차피 이따 실습한 부분에 적어둘 예정이니 거기서 보도록 하자. 파라미터 참고.

5. 실습한 것

각 방법별로 필요한 코드 비워진 곳을 채우고 돌려보는 거였다. 나중에 써먹을 때 참고하기 위해 그대로 옮겨온다.

[Base model]

import keras
import tensorflow as tf
import numpy as np
from tensorflow.keras.datasets import cifar100
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Flatten, Dropout
from tensorflow.keras.optimizers import Adam
from tensorflow.keras import regularizers
import os, random


# seed를 고정합니다.
random.seed(1)
np.random.seed(1)
os.environ["PYTHONHASHSEED"] = str(1)
os.environ['TF_DETERMINISTIC_OPS'] = str(1)
tf.random.set_seed(1)

# 데이터 불러오기
(X_train, y_train), (X_test, y_test) = cifar100.load_data()

# 정규화(전처리)
X_train = X_train / 255.0
X_test = X_test / 255.0  ## => 각 픽셀은 0~255 사이의 정숫값을 가진다. X_train.max()/min()으로 직접 알 수도 있으나 나는 그냥 검색해서 알았다.

## X_train.shape => (50000, 32, 32, 3)
## np.unique(y_train) => 레이블 확인용

# 변수 설정을 따로 하는 방법을 적용하기 위한 코드입니다. 
batch_size = 100
epochs_max = 20

# model
model = Sequential()
model.add(Flatten(input_shape=(32, 32, 3))) 
  ## CIFAR-100 이미지 데이터는 32x32 픽셀의 이미지로, RGB 3채널의 컬러 이미지이다. 이 글을 참고하자. https://keepdev.tistory.com/52 흑백인 경우 이 3을 빼면 될 거다.
model.add(Dense(128, activation='relu'))
model.add(Dense(128, activation='relu'))
model.add(Dense(100, activation='softmax'))

# 컴파일 단계, 옵티마이저와 손실함수, 측정지표를 연결해서 계산 그래프를 구성함
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy'])

results = model.fit(X_train, y_train, epochs=epochs_max, batch_size=batch_size, verbose=1, validation_data=(X_test,y_test))

#결과 확인
test_loss, test_acc = model.evaluate(X_test,  y_test, verbose=1) # loss: 3.3778 - accuracy: 0.2018

[+ Weight Decay]

# seed를 고정합니다.
random.seed(1)
np.random.seed(1)
os.environ["PYTHONHASHSEED"] = str(1)
os.environ['TF_DETERMINISTIC_OPS'] = str(1)
tf.random.set_seed(1)

# 데이터 불러오기
(X_train, y_train), (X_test, y_test) = cifar100.load_data()

# 정규화(전처리)
X_train, X_test = X_train / 255.0, X_test / 255.0

# 변수 설정을 따로 하는 방법을 적용하기 위한 코드입니다. 
batch_size = 100
epochs_max = 20

# model
model = Sequential()
model.add(Flatten(input_shape=(32,32,3)))
model.add(Dense(128, activation='relu', 
                kernel_regularizer=regularizers.l2(0.00001),  ###L2 regularization / param = 0.00001### => 가중치 초기화
                activity_regularizer=regularizers.l1(0.00001)))  ###L1 regularization / param = 0.00001### => 출력값 규제
model.add(Dense(128, activation='relu'))
model.add(Dense(100, activation='softmax'))

# 컴파일 단계, 옵티마이저와 손실함수, 측정지표를 연결해서 계산 그래프를 구성함
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy'])

results = model.fit(X_train, y_train, epochs=epochs_max, batch_size=batch_size, verbose=1, validation_data=(X_test,y_test))

#결과 확인
test_loss, test_acc = model.evaluate(X_test,  y_test, verbose=1) #loss: 3.3056 - accuracy: 0.2169 // baseline model보다 좋아짐.

[+ Dropout]

# seed를 고정합니다.
random.seed(1)
np.random.seed(1)
os.environ["PYTHONHASHSEED"] = str(1)
os.environ['TF_DETERMINISTIC_OPS'] = str(1)
tf.random.set_seed(1)

# 데이터 불러오기
(X_train, y_train), (X_test, y_test) = cifar100.load_data()

# 정규화(전처리)
X_train, X_test = X_train / 255.0, X_test / 255.0

# 변수 설정을 따로 하는 방법을 적용하기 위한 코드입니다. 
batch_size = 100
epochs_max = 20

# model
model = Sequential()
model.add(Flatten(input_shape=(32,32,3)))
model.add(Dense(128*1.1, activation='relu')) # 128*1.1 이거 왜 한거지? 140.8. Dropout 할 때 대강 숫자 맞추기 용도가 있는 것 같은데 아닌가..
model.add(Dropout(0.1)) # => 10% out, only use 90%
model.add(Dense(128, activation='relu'))
model.add(Dense(100, activation='softmax'))

# 컴파일 단계, 옵티마이저와 손실함수, 측정지표를 연결해서 계산 그래프를 구성함
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy'])

results = model.fit(X_train, y_train, epochs=epochs_max, batch_size=batch_size, verbose=1, validation_data=(X_test,y_test))

128*1.1로 한건 뒤에 드롭하는게 10%니까 다른 모델들과 노드 수를 대략 맞춰서 성능 비교하기 좋게 해주려는 의도로 넣어둔거라고 한다.
참고로 128*1.1을 하면 140.8이 나오는데, 원래 노드 수에는 정수형태로 입력되어야 한다고 공식문서에 나와있다. 따라서 이렇게 소수점 자리가 있는 경우 대체적으로 제거가 된 형태로 출력된다고 한다. 반올림 아니고 그냥 140으로 출력! 재밌다. 동기님이 알려주셨다. 감사합니다..!

#결과 확인
test_loss, test_acc = model.evaluate(X_test,  y_test, verbose=1) #loss: 3.3898 - accuracy: 0.1951

[+ Early Stopping]

멈추는 기준을 val_loss(검증 데이터셋의 loss 값)로 하고 loss가 Best 값보다 5번 높아질 때 Stop 하도록 설정합니다.

Best 모델을 저장해봅시다. Best 모델 역시 멈추는 기준을 val_loss(검증 데이터셋의 loss 값)로 하고 save_best_only=True, save_weights_only=True 로 설정합니다.

# seed를 고정합니다.
random.seed(1)
np.random.seed(1)
os.environ["PYTHONHASHSEED"] = str(1)
os.environ['TF_DETERMINISTIC_OPS'] = str(1)
tf.random.set_seed(1)


# 데이터 불러오기
(X_train, y_train), (X_test, y_test) = cifar100.load_data()


# 정규화(전처리)
X_train, X_test = X_train / 255.0, X_test / 255.0


# 학습시킨 데이터를 저장시키기 위한 코드입니다. 
checkpoint_filepath = "FMbest.hdf5"


# 변수 설정을 따로 하는 방법을 적용하기 위한 코드입니다. 
batch_size = 100
epochs_max = 50 # => quiz에서 주어진 조건임.


model = Sequential()
model.add(Flatten(input_shape=(32,32,3)))
model.add(Dense(128, activation='relu'))
model.add(Dense(128, activation='relu'))
model.add(Dense(100, activation='softmax'))

# 컴파일 단계, 옵티마이저와 손실함수, 측정지표를 연결해서 계산 그래프를 구성함
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy'])
                  
# early stopping
# 파라미터 저장 경로를 설정하는 코드
checkpoint_filepath = "IMbest.hdf5" 

early_stop = keras.callbacks.EarlyStopping(monitor='val_loss', min_delta=0, patience=5, verbose=1)

# Validation Set을 기준으로 가장 최적의 모델을 찾기
save_best = keras.callbacks.ModelCheckpoint(
    filepath=checkpoint_filepath, monitor='val_loss', verbose=1, save_best_only=True,
    save_weights_only=True, mode='auto', save_freq='epoch', options=None) # => 파라미터 레퍼런스 https://deep-deep-deep.tistory.com/53

results = model.fit(X_train, y_train, batch_size=batch_size, epochs=epochs_max, verbose=1, 
          validation_data=(X_test,y_test), 
          callbacks=[early_stop, save_best])

# 학습된 모델을 이용하여 테스트하는 코드
test_loss, test_acc = model.evaluate(X_test,  y_test, verbose=1) 
  #loss: 3.3223 - accuracy: 0.2159 => acurracy를 보면 알겠지만 early stopping 지점의 모델 성능임.

model.load_weights(checkpoint_filepath)

# best model을 이용한 테스트 데이터 예측 정확도 재확인 코드
test_loss, test_acc = model.evaluate(X_test, y_test, verbose=1) # loss: 3.3183 - accuracy: 0.2133

7. 그 외

Normalization vs standardization vs regularization
- 우리나라 말로는 다 정규화라고 번역되니 헷갈릴 수 밖에.. (참고한 글)~~(근데 이거 두달 전쯤에도 찾아봤던 것 같은데..)~~ 여긴 간단히만 정리.
- Normalization: 값의 범위를 0~1사이의 값으로 바꾸는 것.
- standardization: 값의 범위를 평균0, 분산 1이 되도록 변환.
- regularization: weight를 조정하는데 규제(제약)을 거는 방법. 과적합 방지를 위해 사용되며, L1(Lasso), L2(Lidge) 등의 종류가 있음.
.hdf5 (혹은 .h5) 파일 형식은 데이터를 계층 구조로 저장하는 하나의 파일 확장자이다. 계층 구조로 저장한다는 의미는 학습별로 가중치를 계층 순서에 따라 저장을 한다고 받아들이면 될 것 같다. hdf5 파일에 대해서는 이 글 참고.

Feeling

딥러닝 들어오니까 정신을 못 차리겠다ㅎ 마음의 여유가 없어진다. 근데 그 와중에 tensorflow 공식문서는 보기 너무 불친절해 화나!!
이전 섹션 회고 때 코치님이 말하길, 보통 섹션3 지나고 섹션4 딥러닝 들어올 때 즈음이면 많이들 동기(motivation)를 잃는다고 하던데 그게 단순히 부트캠프 시작한지 시일이 지나서 그런게 아니라 딥러닝 난이도가 확 올라서 그런 것 같은데요.. 하하..
그래도 난 지지 않아!! 잘 할거야!! 아 글고 부트캠프에서 이번 섹션 기조가 너무 하나하나 깊이 파고들지 말고 내용 잘 이해하고 코드로 구현할 수 있을 정도만 하는 거라고 한다. 음,, 자의반 타의반 그럴 수도 있을 것 같은데 그렇게 넘어가 넘어가 하기엔 좀 불안하기도 하고 말이야..
일단 며칠 더 해봐야알겠다. 그때 다시 생각해보자. 오늘도 고생 많았다~~ 하나 더 배웠어! 어제 나보다는 더 나아진거야!! 어제보다 신경망 모델 조금이라도 더 낫게 만들 수 있게 됐잖아! 와!! 좋아! 짜릿해! 행복해..