Key words
분할정복(divide and conquer), 재귀 호출, 퀵 정렬(Quick Sort), 병합 정렬(Merge Sort)
1. 분할 정복(divide and conquer)
- 분할 정복은 단어에서 보면 대강 어떤 의미인지 추측은 가능할 것이다. 말 그대로 해결하고자 하는 문제를 통으로 한 번에 풀려고 하지 않고, 문제를 분할해서 해결한다는 의미다.
- 좀 더 정확히 말하면,
분할 정복으로 통칭하는 이 패러다임은 한 문제를 유형이 비슷한 여러 개의 하위 문제로 나누어 재귀적으로 해결하고, 이를 합쳐 원래 문제를 해결한다.재귀가 다시 등장한다!!
- 한 문제를 작은 문제로 나누어 풀기 때문에, 어려운 문제를 쉽게 해결할 수 있고, 작은 문제를 풀어 합치는 구조이기 때문에 같은 작업을 더 빠르게 해결할 수도 있다는 장점이 있다.
- 하지만 재귀의 단점으로 지적되었던 것처럼 재귀 함수로 인한 오버헤드 및 스택 오버플로우가 발생할 수 있다는 것은 분할정복의 단점이라고 한다.
분할 정복을 사용하는 알고리즘을 설계할 때는 아래 과정을 기억하면 된다.
- 문제를 더 작은 문제로 분할하는 과정 (divide)
- 작은 문제를 정복하는 과정 (conquer)
- 재귀를 사용하기 때문에 더 이상 문제를 분할하지 않고 곧장 풀 수 있는 매우 작은 문제, 즉 base case가 있어야 한다.
- 각 문제에 대해 구한 답을 원래 문제에 대한 답으로 병합하는 과정(merge)
큰 문제를 작은 문제로 분할한다거나 재귀 알고리즘이 들어간다는 것에 대해서는 이미 다뤄본 적이 있기 때문에 많이 낯선 것은 아니었다.
(재귀가 헷갈리는 개념이라는 것이 문제인거지!)
--
근데 재귀호출과 분할정복의 중요한 차이 하나!!!
- 재귀 호출은 함수 내에 함수 본인을 다시 호출한다는 것이지만, 분할정복에서는 '비슷한 작업을 재진행'하는 것으로 꼭 같은 함수를 호출하는 것은 아닐 수 있다는 것이다. 기억!
다음으로 넘어가기 전에 다시 한 번 기억해야할 것은,
- 난 지금 문제를 해결하는 방식을 말하는 알고리즘을 배우고 있는 것이고, 다양한 알고리즘 중 분할정복을 사용하는 알고리즘에 대해 배운 것이다!!
- 즉, 분할정복 또한 문제 해결 방법 중의 하나인 것이지 항상 효율적인 것은 아니라는 것을 유념하자.
2. 퀵 정렬 (Quick Sort)
- 퀵 정렬의 실제 구현 및 세부 진행 과정에 대해서는 아래 실습 코드에 주석을 상세히 달아두었으므로 여기서는 주요한 특징만을 정리해보려고 한다.
- 퀵 정렬은
피봇이라는 별도의 노드를 지정해두고, 피봇보다 작거나 같은 요쇼/피벗보다 큰 요소를 재귀적으로 정렬하여 문제를 정복해나간다.- 참고로 이 피봇을 처음에 리스트 첫 번째 원소로 지정하기로 했다면, 분할되어 내려가는 서브 노드에서도 마찬가지로 첫 번째 원소가 피봇으로 적용되어 분할된다.
- 무슨 말이냐면,
# 예를 들어 [1,3,5,4,8,9]를 퀵정렬을 이용해 정렬한다고 해보자.
# 피벗을 3으로 지정했다면, 3을 기준으로 노드를 분할한다.
=> [1], [3], [5,4,8,9]로 나뉜다.
# 여기서 각각의 노드는 재귀 호출을 받으며 더 이상 나뉠 수 없을 때까지 쪼개지고(divide),
# 그런 다음에는 가장 작은 문제에서 정복(conquer)된다.
# 그리고 차례로 원래 문제로 병합되어 최종 답을 찾아 나간다.- 퀵정렬은 피벗이라는 별도의 노드를 지정해두는 특성 때문에 가장 빠를 때는
O(nlogn)의 시간 복잡도를 갖지만, 최악의 경우에는 O()의 시간복잡도를 갖기도 한다.O(nlogn)인건, 절반씩 쪼개지니까 logn인거고 그게 n번만큼 내려가니까 앞에 곱해지는 것이다. 최악일 때 O()인 건, 대부분의 원소의 배열을 확인해야하는 건 최선일 때와 같이 n번 수행하지만, 재귀 호출 또한 n번이 일어나기 때문에 n^2인 것이다.- 앞의 n이 이해가 안간다면, 더이상 쪼개질 수 없을 때까지 쪼개 내려가니까 n이 붙은 거라고 이해해도 될 듯.
- 즉, 퀵정렬의 성능은 내가 선택한 기준 원소에 크게 의존한다는 말이다.
- 하지만 그런 최악의 경우가 일반적이지는 않은만큼, 통상적으로 퀵 정렬이 병합 정렬보다는 속도가 빠르다고 알고 있으면 된다.
- 아래 그림은 가장 최선의 케이스에서의 퀵 정렬을 나타낸 것이다.

- 데이터가 딱 반반씩 나뉘는 것이다!
- 최악의 경우는 아래와 같은 경우를 말하는데, 피봇으로 선택한 값이 매번 가장 작거나 가장 큰 값이라서 계속 1개와 n-2개로 분할되는 것이다. (n-1이 아니고 n-2개인 건 하나는 피봇이니까)
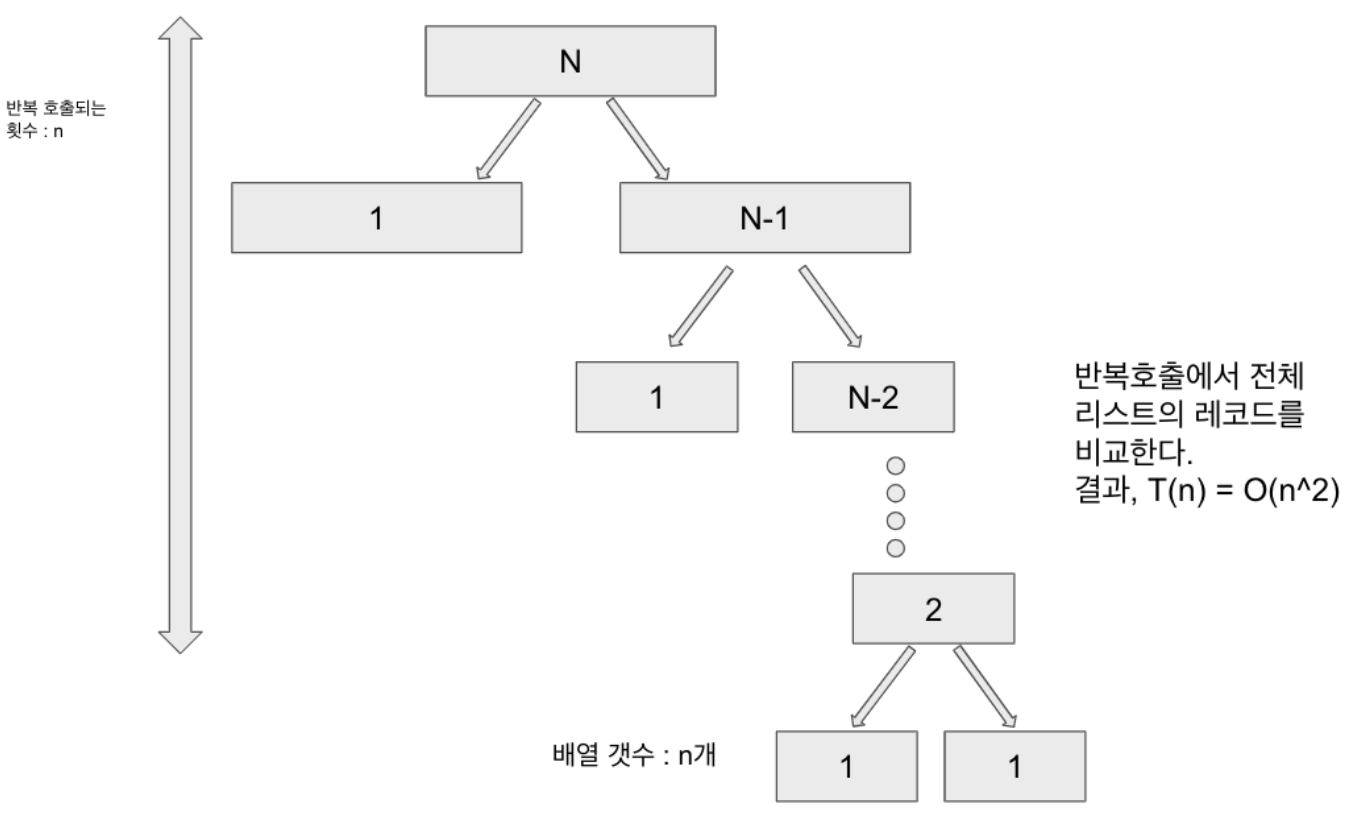
- 퀵정렬은 대표적인 불안정 정렬이다.
- 안정(Stable) 정렬이란?
- 동일한 값을 가지는 데이터가 두 개이상 있을 때, 이 위치가 바귀지 않고 정렬되는 것.
- 예를 들어, [5,5]이면 [5(1), 5(2)]이 안정 정렬이고, 만약 [5(2),5(1)] 이 될 수 있다면 이건 불안정 정렬이라고 함.
- 원소들 중에 같은 값이 있는 경우 이들의 순서가 초기와 달라질 수 있다. 어떤 조건으로 피봇을 나누느냐에 따라!
- 나는 같거나 작은 걸로 할 것이냐, 아니면 같거나 큰 것으로 넣을 것이냐에 따라인 경우를 생각하며 이해했다.
- 안정(Stable) 정렬이란?
3. 병합 정렬 (Merge Sort)
- 머지 소트도 마찬가지로 실제 구현 및 세부 진행 과정에 대한 예시는 아래 실습 코드의 주석을 참고하면 된다.
- 병합 정렬은 매번 중간을 찾아 딱 절반으로 나눈다! 예를 들면 이런 식이다.

- 처음에는 가운데를 기준으로 절반씩 분할해 나가며 더 이상 분할될 수 없을 때까지 내려가고, 그 후 재귀 호출에 의해 병합되며 값을 정렬해나간다. (이건 코드 봐야 이해 갈거야.. 글만 봐선 재귀 과정을 모두 떠올리는게 쉽지 않다.)
- 병합 정렬의 성능은 늘
O(nlogn)이다. 또한 안정 정렬에 속한다.- 퀵정렬보다 빠르지는 않지만 안정 정렬인 특성 때문에 병합 정렬을 활용한다고 한다.
- 또한 퀵정렬처럼 사용자가 지정하는 피봇 같은게 없기 때문에 성능의 편차가 크지 않고 피봇 설정과 같은 다루기 어려운 부분이 없기 때문에 실무에서는 퀵정렬보다는 병합정렬을 선호하는듯?
한 눈에 보는 퀵 정렬과 병합 정렬 비교

- 여기서
내부 정렬,외부 정렬은 정렬한 원소를 담을 새로운 공간이 필요하냐 아니냐를 말한다. 코드 보면 무슨 말인지 안다.
이 블로그 자료도 참고하자.
4. 실습한 것
내가 작성한 주석 보면서 어떤 흐름으로 이루어지는지 과정을 이해하려고 해야 한다!! 외울 생각하지마.. 외우면 어차피 까먹어.. 이해하라고!
[퀵 소트 구현]
def quick_sort(li):
"""
정렬되지 않은 리스트를 매개변수로 받아 오름차순으로 정렬된 리스트를 반환하는
quick_sort를 만들어주세요.
작성되어있는 quick_sort함수를 재귀함수로 사용해주세요.
quick_sort함수 내부에 새로운 재귀함수로 구현하시면 안됩니다.
"""
len_li = len(li)
if len_li <=1: # 재귀 호출 종료 조건. li 원소가 하나만 있으면 정렬이 필요없으므로 그대로 반환한다.
return li
else:
# 첫 번째 원소를 피봇으로 설정. (끝 원소로 지정해도 사실 아래 코드가 크게 달라지진 않는다.)
pivot = li[0]
# pivot보다 큰 값들 모음
greater = [val for val in li[1:] if val > pivot]
# pivot보다 작은 값들 모음
less = [val for val in li[1:] if val <= pivot] # pivot값과 동일한 값을 가지고 있는 경우 해당 값을 잃지 않기 위해 '같다' 조건이 필요하다.
return quick_sort(less) + [pivot] + quick_sort(greater) # 재귀 호출. 이 과정은 복잡하니까 아래 [기록] 부분에 예시로 달아두겠다.
'''
[기록]
- 퀵정렬은 pivot를 정하고 그 값을 기준으로 작은 것은 왼쪽에, 큰 것은 오른쪽에 배열해나가는 식으로 리스트를 쪼갠다. 더이상 쪼개질게 없을 때까지 진행된다.
(pivot은 첫 원소나 끝 원소로 정하는게 보통인 것 같은데, 아무거나 랜덤하게 지정해서 연산이 빨리 끝나길 기도하기도 한다고 한다.)
-재귀 호출 프로세스 따라가보기
[5,9,1,3,7]
[1,3] [5] [9,7] #=> quick_sort(less)와 quick_sort(greater) 각각 재귀 호출.
[] [1] [3] [7][9][] # => len_li = 1 이므로 각각 반환됨.
이게 다시 어떻게 합쳐지는지 아래부터 위로 단계를 밟아보면,
- [1,3]은 원래 quick_sort(less) + [pivot] + quick_sort(greater) 였으므로, [1, 3]이 되고, ([]은 더하나마나니까)
- [9,7] 역시 quick_sort(less) + [pivot] + quick_sort(greater) 였으므로, 아래서 받은 [7,9]가 됨. ([]은 더하나마나니까)
=> 최종적으로 [1,3][5][9,7] 역시 quick_sort(less) + [pivot] + quick_sort(greater) 였는데,
여기서 [1,3]이 [1,3]이고, [9,7]이 [7,9]라는 값을 받았으므로, 최종적으론 [1,3]+[5]+[7,9]가 되어서
[1,3,5,7,9]라는 최종 결과를 리턴하게 되는 것.
그림으로 직접 그려가며 표시하면 위 글보다 훨씬 이해가 쉬운 것 같다.
'''[머지 소트 구현]
def merge(left, right):
"""
문제 1.
두 리스트를 받아 합치는 merge함수를 구현해주세요.
단 매개변수로 들어오는 리스트는 오름차순으로 정렬된 상태의 리스트이며,
반환되는 리스트역시 오름차순으로 정렬된 상태의 리스트여야합니다.
ex)
l = [4,6,7,10]
r = [1,3,9,12]
merge(l,r) => [1, 3, 4, 6, 7, 9, 10, 12]
파이썬에서 제공되는 sort와 같은 내장함수를 사용하면 안됩니다.
"""
res = [] # 정렬해 담아갈 빈 리스트
i = j = 0 # 각 리스트의 첫 번째 원소부터 비교해나갈 것.
while i < len(left) and j < len(right): # 각 리스트에서 비교할 원소가 없어지면 루프 종료.
if left[i] <= right[j]: # left 리스트의 원소가 더 작다면,
res.append(left[i])
i += 1
else:
res.append(right[j])
j += 1
res.extend(left[i:])
res.extend(right[j:])
return res
'''
[기록]
- 위 예시를 통해 함수가 적용되는 과정을 직접 적어보자.
len(left) = len(right) = 4
1) left[0]=4, right[0]=1 이므로, else문 작동되어 res=[1], j = 1 (i = 0 유지)
2) left[0]=4, right[1]=3 이므로, else문 작동되어 res=[1,3] j=2 (i = 0 유지)
3) left[0]=4, right[2]=9 이므로, if문 작동하여 res=[1,3,4] i=1 (j=2 유지)
4) left[1]=6, right[2]=9 이므로, if문 작동하여 res=[1,3,4,6] i=2 (j=2 유지)
5) left[2]=7, right[2]=9 이므로, if문 작동하여 res=[1,3,4,6,7] i=3 (j=2 유지)
6) left[3]=10, right[2]=9 이므로, else문 작동하여 res=[1,3,4,6,7,9] j=3 (i=3 유지)
7) left[3]=10, right[3]=12 이므로, if문 작동하여 res=[1,3,4,6,7,10] i=4 (j=3 유지)
8) i < len(left)가 False이므로 루프 종료. 아직 안 들어간 값은 right의 12.
해당 값을 넣어주기 위해 마지막에 extend를 추가한다.
- 와 이거 처음 고안한 사람 똑똑하네;
- 만약 left, right의 len이 다르다면 마지막 extend가 어떻게 이루어지려나?
> 그래서 조건에 left, right은 모두 오름차순 정렬된 리스트라고 했던거구나. extend도 그런 맥락이고. 이해완료.
'''
@counter # 삭제하거나 변경하지 마세요!
def merge_sort(li):
"""
문제 2.
문제 1에서 만든 merge 함수를 사용하여 merge_sort를 완성해주세요.
정렬되지 않은 리스트를 매개변수로 받아 오름차순으로 정렬된 리스트를 반환하는
merge_sort를 만들어주세요.
작성되어있는 merge_sort함수를 재귀함수로 사용해주세요.
merge_sort함수 내부에 새로운 재귀함수로 구현하시면 안됩니다.
"""
len_li = len(li)
if len_li == 1: # 재귀 호출 종료 조건
return li
mid = len_li // 2
left_partition = merge_sort(li[:mid])
right_partition = merge_sort(li[mid:])
return merge(left_partition,right_partition)
'''
[기록]
- 병합정렬의 경우 중간 지점을 기준으로 2개의 부분배열로 분할하는 과정을 더이상 나뉘지 않을 때(=정렬되었을 때) 반복하고 그것들을 합치는 구조이다.
- 이렇게 나누는 걸 Partition을 나눈다고 한다.
- 일단 이렇게 파티션 나누는 과정을 먼저 직접 표현해보자.
li = [7,6,4,10,3,12,9,1] 이라면, mid = len(li) // 2 = 4번째 원소가 중간 (index로는 3)
> left partition = li[:mid] = [7,6,4,10]
>> 이를 다시 나누면, [7,6]과 [4,10]으로 나뉘는데,
>> 이를 다시 나누면, [7],[6] / [4],[10]으로 나뉜다. 더이상 나뉠 수 없으므로 분할은 종료된다.
>> 이제 여기부터 return에 있는 위에서 작성한 merge 함수가 차례로 돌아간다.
=> merge([7],[6]) = [6,7] / merge([4],[10]) = [4,10]
=> merge([6,7], [4,10]) = [4,6,7,10] 으로 Left partition의 정렬 완료!
> right partition = li[mid:] = [3,12,9,1] 이 된다.
>> 이를 다시 나누면, [3,12]과 [9,1]으로 나뉜다.
>> 이를 다시 나누면, [3],[12] // [9],[1]으로 나뉜다. 더이상 나뉠 수 없으므로 분할은 종료된다.
>> 이제 여기부터 return에 있는 위에서 작성한 merge 함수가 차례로 돌아간다.
=> merge([3],[12]) = [3,12] / merge([9],[1]) = [1,9]
=> merge([3,12], [1,9]) = [1,3,9,12] 으로 right partition의 정렬 완료!
!!이제 최종적으로 left/right partition의 merge가 일어난다.
>> merge([4,6,7,10], [1,3,9,12]) = [1,3,4,6,7,9,10]
재귀의 흐름을 잘 이해하는게 중요할 것 같다. stack처럼 쌓여내려가다가 저장된 계산을 차례로 뱉어내는 방식을.
시간이 지난 다음 다시 보면 또 헷갈릴 수도 있겠다.
'''Feeling
- 논리적 사고력 매우.. 중요!!!!! 잘 할 수 있다.
- 요즘 개인적으로 준비하는 거랑 병행하느라 정신이 좀 없다ㅠㅠ 우선순위 잘 세우고 분할정복하자!
