데이터 사이언스에서 선형대수학이 필요한 이유?

선형대수학이란?

일차식이나 일차함수를 공부하는 학문

• 계수와 변수로 이루어진 일차식
• 행렬의 각각이 하나의 벡터가 되어 형성하는 공간을 ‘벡터 공간’이라고 합니다.
• “벡터로 형성된 공간, 즉 벡터 공간에서 덧셈이나 상수곱 형태의 연산으로 변환을 하고, 그 공간의 성질에 대해 공부하는 것”

❓데이터 사이언스에서 선형대수학이 필요한 이유

물리학자: 벡터를 공간상 화살표로 생각하는 방식 → 좋은 수적 표현 가능
컴퓨터 과학자: 숫자의 배열로 생각하면 좋은 기하적 표현 가능

• 위 방식을 쓰냐 마냐 중요하지 않습니다.
• 선형대수학의 용도는 이 두관점을 다루는 것이 아니라, 어떤 대상의 상호작용을 해석하는능력을 다루는 것입니다.
• 데이터 속 패턴을 설명하고, 어떤 연산들에 관한 보편적인 관점을 제공하죠.
• 다른 한편, 선형대수학은 물리학자나 컴퓨터 그래픽 프로그래머에게 공간과 공간의 조작을 숫자를 사용하여 묘사하는 언어를 제공하여, 컴퓨터에서 구현할 수 있도록 합니다.

직접적인 이유로는

1. 우리가 다루려는 대부분의 데이터가 행과 열로 구성된 “행렬 매트릭스”로 벡터로 표현할 수 있기 때문입니다. 데이터 처리의 기본 단위로 벡터 또는 행렬을 이용할 수 있어요!
2. 선형대수학의 수식과 계산 기법을 사용하면 최소한의 타이핑 만으로도 대량의 계산을 손쉽게 컴퓨터에게 지시할 수 있고 연산이 훨씬 빨라집니다.
3. 선형대수학은 데이터 분석가에게 많은 숫자의 배열을 시각적으로 개념화하기 좋은 방법을 제공합니다.

• 중요한 데이터를 뽑아낼 때 사용하는 방법
  • 차원축소, PCA(주성분분석),Word2Vec 을 이용합니다.
• 이미지 인식에 많이 활용되는 딥러닝(인공 신경망), 추천 알고리즘 모두 기본 행렬 벡터 공간에서 이루어지는 계산입니다.
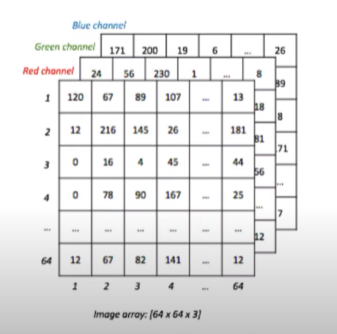
  • e.g) 개와 고양이 인식 머신러닝에서 각각의 이미지를 숫자로 이루어진 행렬로 벡터화해서 처리하는 것이고 이미지는 RGB값으로 나눠진 숫자로 이루어져 있습니다.

• 따라서, 선형대수학은 모든 공학, 수학, 과학 분야의 기초 수학 과목입니다. 그리고 게임 그래픽 처리까지 현대 기술의 여러 분양의 근간을 이루는 중요한 기초수학 과목으로 공부해야합니다.