선형대수

선형대수의 시작

벡터의 시각화

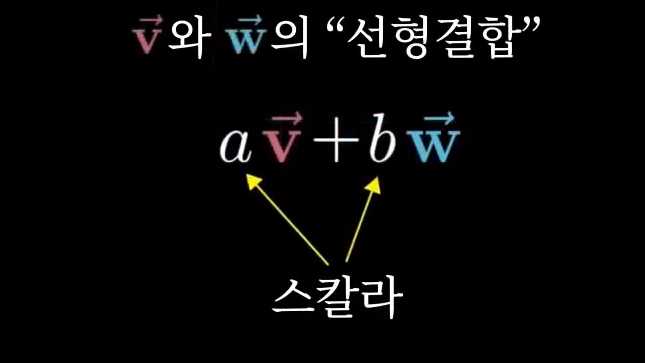
선형결합, 생성, 기저벡터 💡 “수학은 천재가 아닌, 적은 양의 상상의 자유를 필요로 한다. 덧붙여, 더 많은 양에서의 그것을 우린 광기라 부른다” - 수학자 앵거스 K. 로저스 선형결합 > 두 벡터를 스케일하고 더하여 새 벡터를 얻는 모든 연산을 저 두벡터의 선형결합이라고 부릅니다. > 각 좌푯값을 스칼라로써 생각해보시기 바랍니다. 그러니까, ...

Span > 주어진 벡터들의 조합(합, 차 등)으로 만들 수 있는 가능한 모든 벡터의 집합. 즉, 공간입니다.사용하는 벡터에 따라 모든 공간을 채울 수도, 부분적인 공간만 채울 수도 있습니다. > 선형 관계의 벡터(즉, 선형종속)은 조합을 통해 선 외부의 새로운

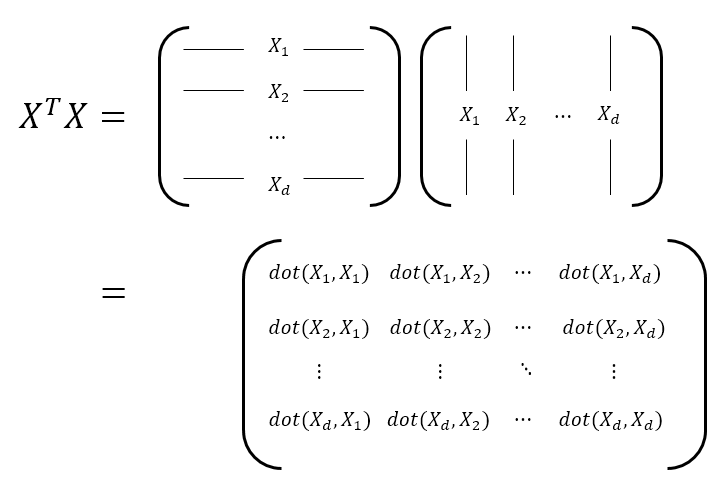
공분산(covariance) 두 변수에 대하여 한 변수가 변화할 때 다른 변수가 어떠한 연관성을 갖고 변하는지를 나타낸 값입니다. 두 변수의 연관성이 클수록 공분산 값도 커집니다. 공분산 행렬(covariance matrix) > 기하학적 의미 행렬 = 선형변환, 벡터 공간을 다른 벡터 공간으로 mapping > > 데이터 구조적 의미 각 featu...

고유벡터(Eigenvector) > 함수를 통해 선형변환 할 때 크기만 변하고 방향은 변하지 않는 벡터입니다. 그 행렬이 벡터의 변화에 작용하는 주축(principal axis)의 방향을 나타냅니다. 즉, 공분산 행렬의 고유벡터는 데이터가 어떤 방향으로 분산되어 있는지 찾아줍니다. 고유값(Eigenvalue) > $T(v) = \lambda v \...

linear projection(선형 투영) > Projection이란 한 벡터를 다른 벡터의 공간에 표기하는 것이라고 생각할 수 있습니다. > 아래 그림에서 vector b를 vector a 위의 vector p 로 projection 한 것이다.vector a가 선(1차원) 위에 있는 경우, vector p는 아무리 스케일을 변화시켜도 결국 선 위에 ...

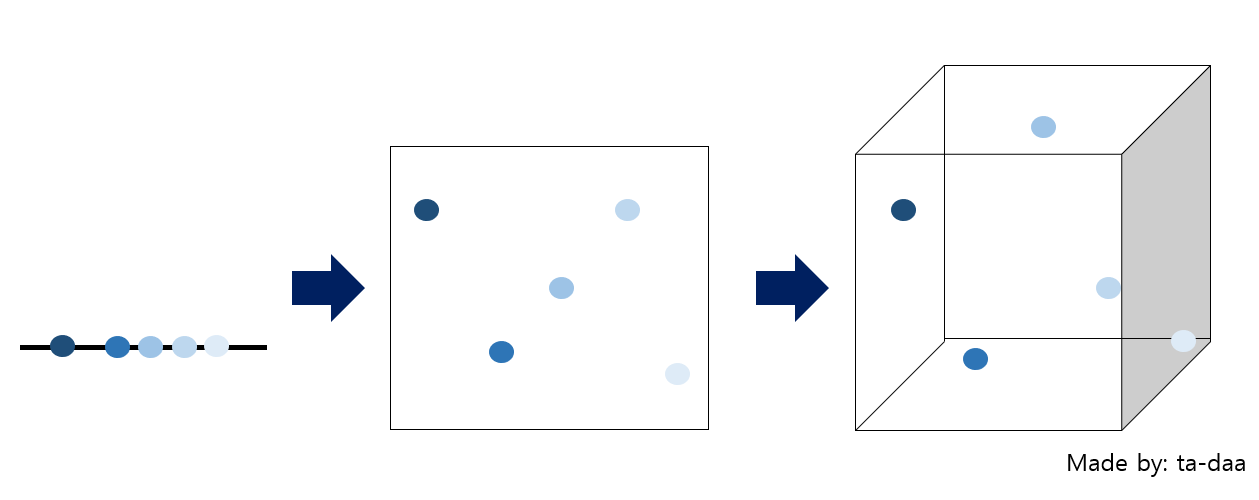
차원의 저주란 > 데이터 학습을 위해 차원이 증가하면서 학습데이터 수가 차원의 수보다 적어져 성능이 저하되는 현상. 차원이 증가할 수록 개별 차원 내 학습할 데이터 수가 적어지는(sparse) 현상 발생 즉, 데이터보다 차원의 수가 더 많을 때 발생하는 현상입니다. 무조건 변수의 수가 증가한다고 해서 차원의 저주 문제가 있는 것이 아니라, 관측치 수보다 ...

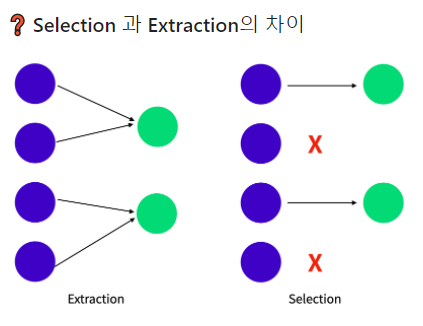
정보 손실은 최소화(가능한 많은 정보를 포함)하면서 중요한 변수만 선택할 수 있다면 어떨까요?머신러닝에서는 이를 위한 다양한 차원 축소 기술들을 연구 중입니다. > 차원 축소란 고차원 원본 데이터의 의미 있는 특성을 이상적으로 원래의 차원에 가깝게 유지할 수 있도록 고차원 공간에서 자차원 공간으로 데이터를 변환 하는 것을 말합니다. > > - 직관적으로 ...

PCA의 원시적 의미 > 종합점수를 계산하는 방법 > > 100명 학새들의 국어와 영어 시험 성적에 대해 종합점수를 잘 내려면? 벡터의 내적(정사영)을 통해 표현 데이터 벡터를 어떤 벡터에 내적(혹은 정사영)하는 것이 최적의 결과를 얻어 주는가? 기왕 정사영 할 벡터(혹은 축)를 찾는데, 데이터 분포의 중심을 중심축으로 하는 벡터를 찾는제 좋지 않을까? ...

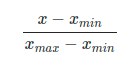
normalization(정규화) 정규화의 목적은 데이터셋의 numerical value 범위의 차이를 왜곡하지 않고 공통 척도로 변경하는 것입니다. 기계학습에서 모든 데이터셋이 정규화 될 필요는 없고, 피처의 범위가 다른 경우에만 필요합니다. 값의 범위(scale)을 0 ~ 1사이의 값으로 바꿔주는 것. 학습 전에 scaling하는 것 머신러닝에서 s...