[알고리즘] 펜윅 트리 Fenwick Tree

cup-wan·2025년 7월 27일

bit fenwick tree 알고리즘 펜윅 트리

Algorithm

목록 보기

3/5

Why?

백준 2243. 사탕상자

이분 탐색 문제를 풀기 위해 접한 문제라 당연히 이분 탐색으로 먼저 접근했습니다.
단순 이분 탐색으로 풀다보니 모든 구간에 대한 누적 개수를 구하기 어려웠습니다.
해당 문제의 핵심은 구간별 개수를 유지하면서 순위 (k번째 작은 원소) 조회를 지원하는 알고리즘입니다.

구간 합 문제라 생각해서 세그먼트 트리가 먼저 생각났으나 검색해보니 펜윅 트리가 있어서 해당 알고리즘에 대해 알게됐습니다.

기본 개념

펜윅 트리는 1994년 논문이 발표된 비교적 최신 알고리즘이다.
PS에서는 세그먼트 트리로 풀 수 있는 문제 중 메모리를 절약할 수 있는 장점이 있어서 사용된다.

누적합 (prefix sum)

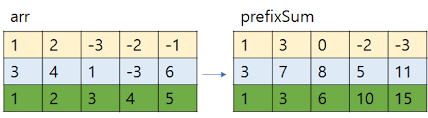
누적합 알고리즘은 1 ~ N 까지의 합 배열을 따로 만들어 구간합을 O(1)로 구할 수 있습니다.
1 ~ N 배열의 값이 변경(update)되면 누적합 배열을 전부 다시 계산해야하므로 O(N)의 복잡도를 갖게됩니다.

펜윅 트리 (fenwick tree)

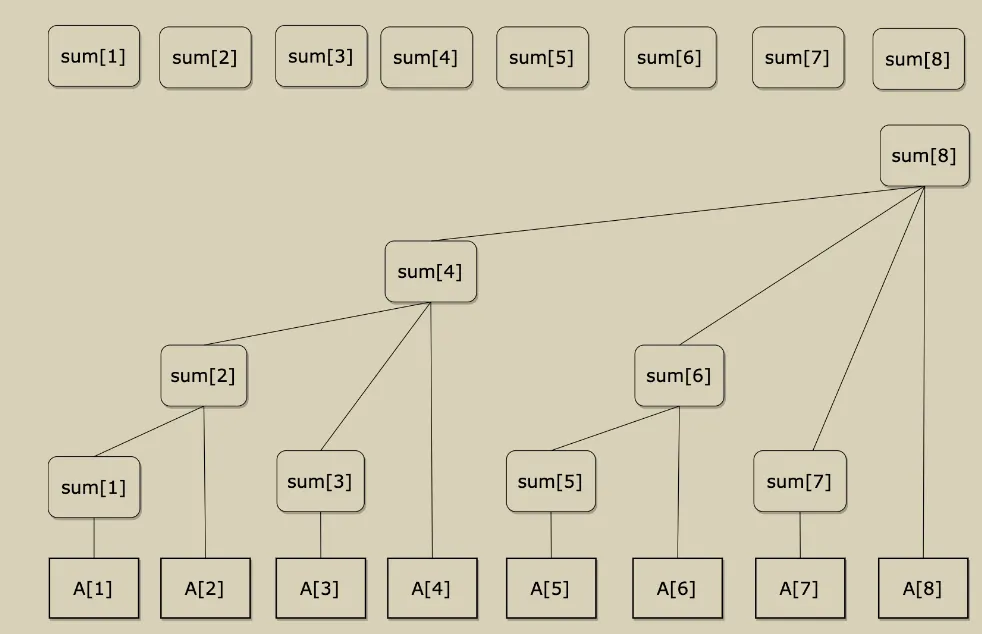
펜윅 트리는 누적합에서 변경(update)을 더 빠르게 하기 위해 사용합니다.
구간합, 배열값 변경 모두 O(logN)의 복잡도를 갖습니다.
세그먼트 트리 구성을 위해 약 4N의 메모리가 필요한 것과 달리 기존 배열 크기인 N만큼의 메모리만 필요합니다.
세그먼트 트리보다 코드가 매우 간단합니다.

방식	업데이트	구간 합
단순 배열	O(1)	O(n)
Prefix Sum	O(n)	O(1)
Fenwick Tree	O(log n)	O(log n)

구현

⚙️ Setting

기존 배열 : arr = [1,2,3,4,...,16]

펜윅 트리 : tree = int[16]

핵심 연산 :

구간 합 (query) : 1부터 특정 인덱스까지의 구간 합을 구합니다.

값 변경 (update) : 특정 인덱스의 값을 변경 후 연관된 구간 합을 갱신합니다.

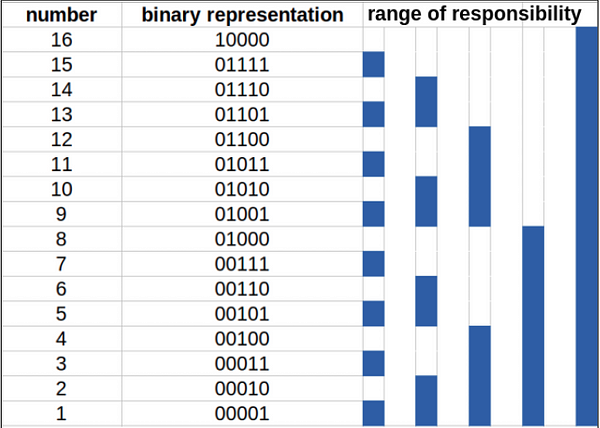
핵심 아이디어 : Range of Responsibility

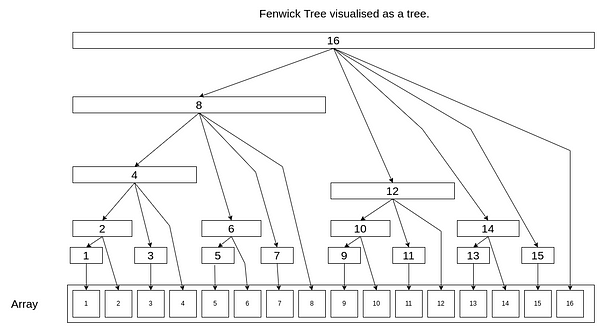
펜윅 트리는 겉보기엔 단순 1차원 배열이지만, 내부적으로는 이미지처럼 계층적인 트리 구조 규칙을 따릅니다. tree 배열의 각 칸(노드)은 원본 배열(arr)의 특정 구간에 대한 합을 "책임"집니다.

tree[8]은 arr[1]부터 arr[8]까지 8개 원소의 합을 책임짐.
tree[12]는 arr[9]부터 arr[12]까지 4개 원소의 합을 책임짐.
tree[7]은 arr[7]부터 arr[7]까지 1개 원소 (=자기 자신)값만 책임짐.

최하위 비트(LSB)가 이 Range of Responsibility를 정합니다.

최하위 비트 (LSB, RSB)

최하위 비트 (Least Significant Bit, LSB)는 어떤 숫자를 이진수로 표현했을 때 가장 오른쪽에 있는 1의 값을 의미한다. 1의 위치가 아닌, 1이 나타내는 실제 값임에 주의한다.

12 → 1100₍₂₎ → 가장 오른쪽의 1은 뒤에서 세 번째 자리에 있습니다. (LSB = 4)
7 → 0111₍₂₎ → 가장 오른쪽의 1은 맨 뒷자리에 있습니다. (LSB = 1)
8 → 1000₍₂₎ → 가장 오른쪽의 1은 뒤에서 네 번째 자리에 있습니다. (LSB = 8)

바로 이 LSB값이 각 tree 인덱스가 책임지는 원소의 개수가 됩니다. 이 LSB는 다음과 같은 비트 연산으로 간단하게 구할 수 있습니다.

LSB = i & -i

현재 값과 2의 보수의 AND 연산만으로 LSB값을 구할 수 있습니다.

[예시]
// 12의 LSB 구하기
12  = 00001100
-12 = 11110100  (2의 보수 표현)
-----------------
&     00000100  (결과는 4)

// 7의 LSB 구하기
7   = 00000111
-7  = 11111001
-----------------
&     00000001  (결과는 1)

이제 tree[i]가 몇 개의 원소를 책임지는지 알게 되었습니다. 이를 바탕으로 update와 query를 구현할 수 있습니다.

update : 값 변경 후 갱신

원본 배열 arr[i] 값을 변경 시 arr[i]를 포함하는 모든 구간 합들을 찾아 값을 갱신해야합니다. tree에서 i번 노드의 변경으로 영향을 받는 모든 노드를 수정해야합니다.
이 영향을 받는 노드 또한 LSB를 통해 구할 수 있습니다. 특정 인덱스 i에서 시작하여 자신의 LSB값을 더해주면 다음으로 갱신할 상위 노드의 인덱스로 이동할 수 있습니다.

다음 인덱스 = i + (i & -i)

[예제] update(3, 5) : arr[3] += 5

i=3: tree[3]에 5를 더하기
다음 인덱스 : 3 + (3 & -3) = 4
i=4: tree[4]에 5를 더하기
다음 인덱스 : 4 + (4 & -4) = 8
i=8: tree[8]에 5를 더하기
다음 인덱스 : 8 + (8 & -8) = 16
i = 16: tree[16]에 5를 더하기
다음 인덱스 : 16 + (16 & -16) = 32 (배열 범위 밖이라 종료)

이 예제를 통해 arr[3]이 변하면 tree[3], tree[4], tree[8], tree[16] 순서대로 전파되는 것을 알 수 있습니다.

이를 코드로 구현하면 다음과 같습니다.

public static void update(int i, long val) {
   // i가 배열 크기 N을 넘지 않을 때까지 LSB를 더해가면서 val을 더함
   while (i <= N) {
       tree[i] += val;
        i += lsb(i);
   }
}

query : 1부터 N까지의 합 구하기

1부터 i까지의 누적 합을 구하는 과정은 update와 반대입니다. i에서 시작해, 자신의 LSB값을 빼주면서 0이 될 때까지 만나는 모든 노드의 값을 더하면 됩니다.
각 노드들이 책임지는 구간들은 서로 겹치지 않기 때문에, 이들을 더하면 정확히 1부터 i까지의 합이 완성됩니다.

다음 인덱스 = i - (i & -i)

[예제] query(13) : arr[1] + arr[2] + ... + arr[13]

i = 13: sum에 tree[13]을 더하기. (tree[13]은 arr[13]의 합)
다음 인덱스: 13 - (13 & -13) = 13 - 1 = 12
i = 12: sum에 tree[12]를 더하기. (tree[12]는 arr[9]~arr[12]의 합)
다음 인덱스: 12 - (12 & -12) = 12 - 4 = 8
i = 8: sum에 tree[8]을 더하기. (tree[8]은 arr[1]~arr[8]의 합)
다음 인덱스: 8 - (8 & -8) = 8 - 8 = 0 (0이 되었으므로 종료)

이를 코드로 구현하면 다음과 같습니다.

public static long query(int i) {
    long result = 0;
    // i가 0보다 클 때까지 LSB를 빼가면서 tree 값을 더함
    while (i > 0) {
       result += tree[i];
        i -= lsb(i);
    }
    return result;
}

세그먼트 트리와 같이 부분 합을 구하기 위해서는 query 연산을 두번 해야합니다.
예를 들어 3~7 구간합을 구하기 위해서는 query(7) - query(2)을 해야합니다

사탕 상자 풀이

B, C가 주어질 때 : C개의 B 맛 사탕 넣기 or 꺼내기. 이는 B라는 인덱스의 값을 C만큼 변화시키는 것 = query(B,C)
A가 주어질 때 : A번째로 맛있는 사탕 꺼내기. 누적 합이 A 이상이 되는 최초의 맛(인덱스)가 무엇인가요?`
- 기존의 query만으로는 부족
- 해당 조건을 만족하는 값을 이분 탐색을 통해 해결해야함.
- 펜윅 트리를 응용한 k번째 원소 찾기 기법
- 가장 큰 2의 거듭제곱부터 시작해서, 현재 인덱스의 사탕 개수를 확인하며 이진 탐색처럼 아래로 내려오는 방식으로 원하는 순위의 사탕을 찾기

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class Main {

    static final int MAX = 1_000_000;
    static int[] fenwick = new int[MAX+1];

    static void update(int idx, int val) {
        while(idx <= MAX) {
            fenwick[idx] += val;
            idx += idx & -idx;
        }
    }

    static int find(int rank) {
        int idx = 0;
        for(int i = (int)Math.pow(2, 20); i > 0; i /= 2) {
            if(idx + i <= MAX && fenwick[idx+i] < rank) {
                rank -= fenwick[idx + i];
                idx += i;
            }
        }
        return idx + 1;
    }
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st;
        StringBuilder sb = new StringBuilder();
        int N = Integer.parseInt(br.readLine());
        for(int i = 0; i < N; i++) {
            st = new StringTokenizer(br.readLine());
            int cmd = Integer.parseInt(st.nextToken());
            if (cmd == 1) {
                int rank = Integer.parseInt(st.nextToken());
                int taste = find(rank);
                sb.append(taste).append("\n");
                update(taste, -1);
            }else {
                int taste = Integer.parseInt(st.nextToken());
                int cnt = Integer.parseInt(st.nextToken());
                update(taste, cnt);
            }
        }
        System.out.println(sb);
    }
}