Games for AI: Movement

Movement

Movement algorithm structure

• 캐릭터 = 현재 포지션(velocity) + 물리적 특성
• 모든 움직임 알고리즘은 같은 기본형태를 띈다: own state, world state, geometric output

• 보통 velocity에 대한 출력이 기본임
• Kinematic movement: 캐릭터가 어떻게 가속(accelerate)하고 느려지는 것이 중요하지 않음(단순히 움직이는 방향만 따짐)
• Dynamic movement: 캐릭터의 현재 동작이 중요함(캐릭터의 velocity를 바꾸는 목표를 가진 힘이나 방향 = velocity)

Basics of Movement Algorithms

2차원 움직임

• 점에서의 캐릭터: 많은 움직임 알고리즘은 한 점에서 다루어질 수 있다.
• 충돌 방지, 장애물 회피와 다른 비슷한 알고리즘들은 캐릭터의 크기에 영향을 주지만 움직임은 캐릭터가 그 점에 있다고 판단함

Statics

• 2차원 공간
• 2차원에서 x와 z축
• CCW angle, in radians, from the positive z-axis 사용
  

Kinematics

• 위치와 방향(orientation)만으로 목표 속도(velocity)를 계산하는 이동 알고리즘을 만들어 출력 속도를 즉시 변경할 수 있음
• Linear velocity: x, z 두 요소가, 축에서의 캐릭터의 속도
• Angular velocity: 캐릭터의 방향이 얼마나 빠르게 바뀌나(각 속도)
  

Steering behaviors

• 레벨 주변으로 캐릭터의 속도를 변경하려는 가속도 리턴
  

• 많은 프레임 = 부드러운 모션
  

• 프레임 속도가 높을 수록, 이 함수가 통과되는 속도는 매우 짧다.(업데이트가 빠름)

Kinematics Movement Algorithms

• static data 사용(위치+각도, 속도는 X)하고 velocity 출력
• Kinematic 알고리즘은 가속 사용 X

Seek

• Input: 캐릭터, 타겟의 static data
• 캐릭터 -> 타겟의 방향 계산 및 해당 경로 속도 요청
  

Flee

• Seek의 steering.velocity 방향만 반대로 바꿔주면 됨

Arriving

• 캐릭터가 게임 세계의 특정 지점으로 이동하는 경우 이 알고리즘은 문제 있을 수 있음
• 항상 Full speed로 움직이기 때문에 정확한 지점을 오버슈팅할 가능성이 높음

• 알고리즘에 큰 radius 범위를 준다
• 다양한 속도를 지원하면, 캐릭터의 속도를 늦츨 수 있음
  
• 더 높은 값은 부드러운 감속, 낮은 값은 제동이 급격해짐

Wandering

• 운동학적 방황 거동은 항상 최대 속도로 캐릭터의 현재 방향으로 이동합니다
• 스티어링 동작은 캐릭터의 방향을 수정합니다
  

Steering Behaviors

• velocity와 rotation을 추가함으로써 이전 섹션의 움직임 알고리즘을 확장한다.
• 캐릭터의 키네마틱과 제한된 양의 타겟 정보 입력

Variable matching

• 하나 이상의 캐릭터 키네마틱 요소와 타겟 키네마틱 요소를 맞추자
• 키네마틱 두 가지 이상의 요소가 동시에 일치할 때?
  • 각 요소에 대해 개별 맞춤 한 다음에 결합해서 한다

Seek and Flee

• 키네마틱 Seek 알고리즘에서는 정확히 타겟을 향한 방향을 찾고 가능한 빨리 목표를 향한다.
• steering output은 현재 가속이기 때문에 최대 가속될 수 있다
  

Arrive

• 탐색: 가능한 한 최대의 가속으로 항상 목표를 향해 나아갑니다
• 캐릭터가 목표물에 도착하면 오버슈팅됨
• 정확한 위치에 정확히 도착하도록 속도를 줄여야 함(키네마틱 도착 알고리즘)

Arrive(Dynamic)

• 두 개의 radii를 사용
• The arrival radii: 캐릭터를 대상에 가깝게 설정
• Second radii: 더 크고 들어오는 캐릭터는 이 반경을 통과할 때 느려질 것임
  • 감속 반경에서 이는 최대 속도와 같습니다.
  • 목표 지점에서는 0입니다(도착 시 속도가 0이 되길 원합니다).
  • 그 사이에 원하는 속도는 보간된 중간 값으로 타겟과의 거리에 의해 제어됨

class Arrive:
    # Kinematic 데이터(캐릭터, 타겟)
    charater
    target

    # 캐릭터의 최대 가속력과 속도
    maxAcceleration
    maxSpeed

    # 타겟에 도착하기 위한 범위(radius)
    targetRadius

    # 느려지기 시작하는 범위(radius)
    slowRadius

    # 타겟 속도에 도달하기 위한 시간
    timeToTarget = 0.1

    def getSteering(target):

        steering = new SteeringOutput()

        # 타겟까지의 방향
        direction = target.position - character.position
        distance = direction.length()

        # 범위 내에 있으면 리턴x
        if distance < tagetRadius:
            return None

        # slowRadius 밖에 있으면 최대 속도 출력
        if distance > slowRadius:
            targetSpeed = maxSpeed

        # slowRadius 안에 있으면 속도 조절
        else:
            targetSpeed = maxSpeed * distance / slowRadius

        # 타겟 velocity(속도와 방향 결합)
        targetVelocity = direction
        targetVelocity.normalize()
        targetVelocity *= targetSpeed

        # target velocity까지 가속 시도
        steering.linear = targetVelocity - character.velocity
        steering.linear /= timeToTarget

        # 가속이 너무 빠르면
        if steering.linear.length() > maxAcceleration:
            steering.linear.normalize()
            steering.linear *= maxAcceleration

        # steering 출력
        steering.angular = 0
        return steering

Align

• Align은 캐릭터의 방향을 target과 일치시키려 한다.(캐릭터나 타겟의 위치나 속도에 주의를 기울이진 않음)
• target 방향에 도달하기 위해 시도하고 도달하면 회전이 0이 되도록 한다.(arrive와 비슷하게 작동)
• 2pi 마다 반복되니깐 단순히 빼는 걸로 단순화 못 시킴 (-pi, pi)로 해야됨

Velocity matching

• 캐릭터가 target의 움직임을 모방하도록 사용될 수 있지만 유용하진 않음
• 다른 행동들을 결합하면 중요함(플로킹 스티어링 동작의 구성 요소 중 하나)

Wander

• kinematic 방황 행동, 방황 방향이 실행될 때마다 무작위 양으로 교란되었습니다(캐릭터의 회전이 불규칙합니다)
  • target이 제한된 캐릭터 주변 원 내에 있다
  • 행동이 실행될 때마다, 랜덤한 양만큼 원 주위로 조금씩 움직인다
  • 그런 다음, 캐릭터는 타겟을 찾는다

Path following

• 타겟까지의 모든 경로를 가지는 조종 행동(Steering behavior)
• 현재 캐릭터의 위치와 경로의 모양을 기반으로 target의 위치를 계산한다
• target을 찾는 법
  • 고정된 거리에 의한 맵의 점과 경로를 따라 가장 가까운 점을 찾음
  • 짧은 시간 내 캐릭터가 있을 지점을 예측하고 1번을 반복한다(예측 경로 탐색)

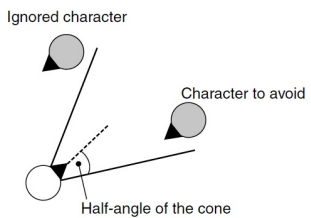
Collision avoidance

• 캐릭터는 다른 움직이는 캐릭터와 충돌을 피해야 함

• 'half-angle of the cone'을 이용하고 회피(evade) 또는 분리 동작을 한다

• 원뿔 내 다른 캐릭터들이 있으면?

  • 원뿔 내 모든 캐릭터의 위치와 속도의 평균을 찾는다
  • 가장 가까운 캐릭터만 고려하고 나머지는 무시한다
    

• Panic
  

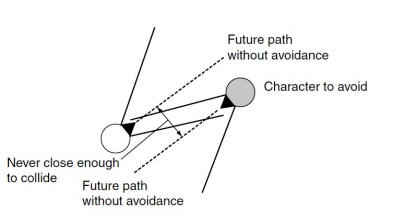
• Evasive action
  

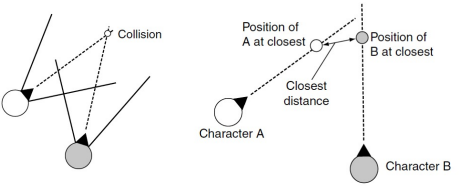
  • 충돌 예측을 통해 충돌을 회피함
  • 경로가 교차하는지는 판단할 수 없지만 가장 가까이 있는 순간을 찾고 분리를 유도함

Obastacle and wall avoidance

• 캐릭터는 움직이면서 해당 방향으로 하나 이상의 광선을 발사함
  
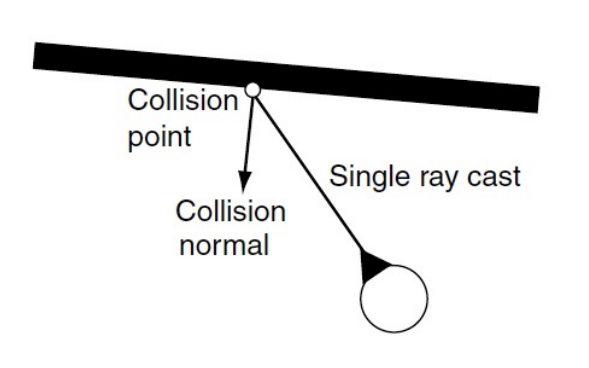
• ray cast로 충돌 지역 감지하면 collision point에서 수직인 collision normal(벡터)를 이용해 빠져나간다
  
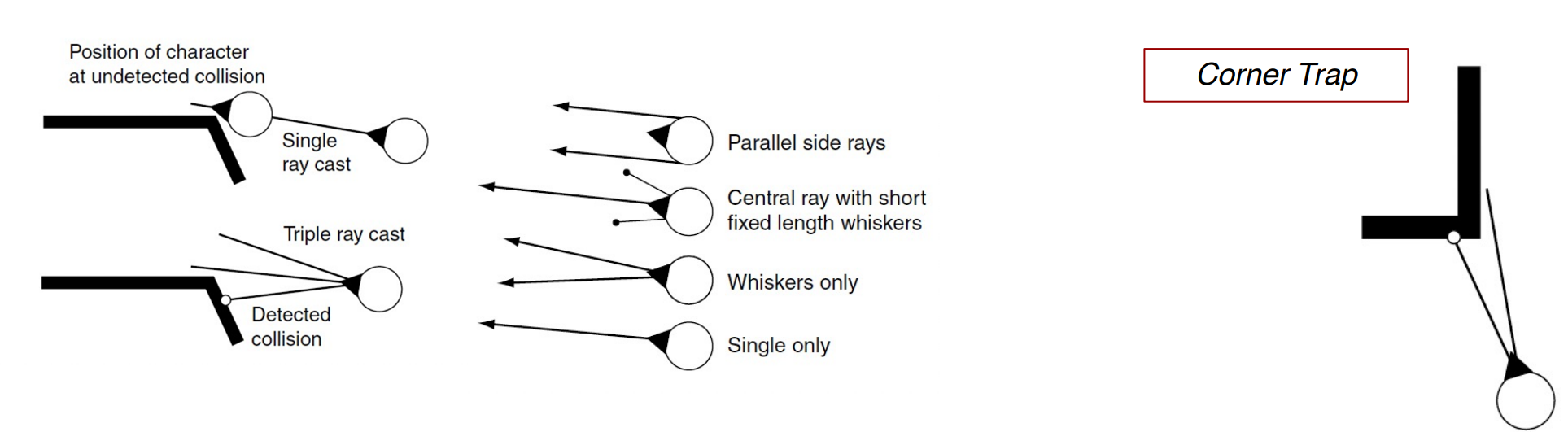
• 광선 하나 쓰는 건 별로임
• 근데 뭐가 낫고 좋은지 아직 기준이 없음
• 짧게 나가는 단일 광선이 초기 설정으론 좋은데 캐릭터가 좁은 통로를 따라 이동하는 것이 불가능할 수도 있음
• 평행으로 하면 모서리가 무딘 곳에서는 잘 작동하지만 뾰족한 곳에선 잘 작동을 못 함 = Corner Trap 현상
• 충분히 넓은 각을 지닌 부채꼴 모양으로 해결 가능
  • 넓은 각 => 모서리 통과 가능
  • 작은 각 => 작은 통로를 통과할 수 있음
    • 각을 넓고 작게 조절하면서 적응형 각도를 만듦
    • 특정한 corner trap 회피 코드 구현

Games for AI: Path Finding

Path Finding

• 어디로 이동할지 + 어떻게 이동할지
• 대부분의 게임은 A* 알고리즘 사용 -> 음수가 없는 가중치 그래프가 필요함

Path Finding Graph

• 그래프 형태로 표현, 단순화된 버전
• 단순화 과정에서 정보를 버리는데 이 정보가 중요할 수도 있음(단순화가 제대로 되지 않으면 최종 경로가 그다지 좋지 않을 수 있음)

Graph

• 방향성 비음수 가중치 그래프를 사용한다
  • 그래프에 점이나 원은 노드
  • 노드끼리 선으로 연결되어 있음
• 그래프는 노드 집합과 연결 집합으로 구성된다, 연결은 정렬되지 않은 노드쌍

Weighted Graph

• 각 연결에 노드 쌍에 추가하여 수치 값을 추가한다
• 길찾기 그래프에서 비용은 시간이나 거리를 나타냄
• 최종 경로 비용: 경로에서 각 연결의 비용 합
  

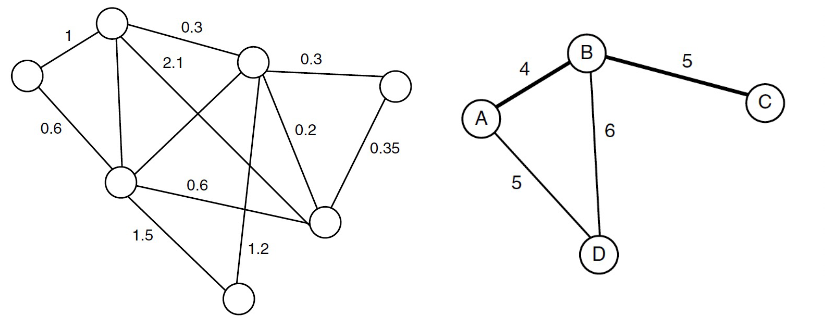
비음수 제약조건

• 수학적 그래프 이론은 음수 가중치를 허용함
• 다익스트라와 A* 알고리즘은 비음수 가중치에만 사용 가능함
• 비용: 비음수 가중치

방향 가중 그래프

• 연결이 한 방향으로만 되어 있다고 가정
• 다음과 같은 상황에서 유리함
  • A에서 B로 움직이는 능력이 A에서 B로 도달할 수 있다는 것을 항상 의미하는 것은 아님
  • 다른 방향의 두 연결을 가지는 것은 두 개의 다른 비용이 있을 수 있다는 것을 의미

Dijkstra

• 게임에서 길찾기는 출발지점과 도착지점을 가질 때, 최단 경로 알고리즘은 초기 지점으로부터 어디로든 최단 경로를 찾을 수 있게 만들어짐
• 다익스트라는 주 경로 찾기 알고리즘 보다는 production 길찾기로 쓰임

문제점

• 두 노드가 하나 이상의 연결로 이루어져 있으면 각 연결마다 다른 비용을 가질 수 있음

진행 방식

• 다익스트라는 시작 노드의 연결을 따라 퍼져가는 식으로 작동
• 더 먼 노드들로 퍼져 나가면서, 자신이 온 방향을 기록한다
• 다익스트라는 퍼지는 과정을 조절하기 때문에, chalk arrow가 항상 시작까지의 최단 경로를 따라 뒤로 향하도록 보장?
• 다익스트라는 반복함
  • 각 반복은 그래프의 한 노드를 고려하고 밖으로의 연결을 따름
  • 반복에서 노드를 '현재 노드'라고 한다

current Node

• 반복 하는 동안, 다익스트라는 현재노드에서 밖으로의 연결을 고려함
• 각 연결은 끝 노드를 찾고 경로의 총비용("cost-so-far" = 현재까지의 비용)을 저장하고 거기로부터 도착한 연결을 저장함

Node list

• Open list: 보이는 모든 노드들을 기록하지만 아직 반복은 안 함
• Closed list: 처리된 노드들을 추적한다
• 각 노드들은 3가지 형태로 있음: closed, open, unvisited
  • 반복 중, 알고리즘은 가장 작은 총 비용을 가진 open list의 노드를 선택함
  • 그 후 처리된 노드는 open list에서 제거되고 closed list로 옮겨짐

총 비용(Cost-so-far)과 closed node는 어떻게 계산하나?

• 우리가 이미 찾은 경로보다 더 나은 경로를 찾았는지 확인함
• 새로운 총비용 값이 최근 총비용보다 작으면, 더 나은 값으로 바꾸고 연결을 기록한다. 그 후 노드는 open list에 옮겨둔다
• 이전에 closed list에 있었다면, 제거한다.
  -> 다익스트라는 절대 closed node까지의 더 나은 경로를 찾을 수 없음

종료 조건

• 기본 다익스트라 알고리즘은 open list가 없을 때 종료된다
• 그래프의 모든 노드는 시작 노드로부터 도달되어야 하고 closed list에 모두 있어야 함
• 길찾기를 하는 동안, 오직 목표 노드 도달에만 관심있으므로 빨리 멈출 수도 있음
• 목표 노드가 open list에서 가장 작은 노드 일 때 종료되어야 함

목표를 찾은 즉시 종료하는 건 어떤가?

• 이 규칙은 종종 깨진다
• 목표에 도달하는 첫 경로는 매우 짧은 경우가 많으며 더 짧은 경로가 존재할 때도 조금만 길어짐

경로 검색

• 최종 단계는 경로를 검색하는 것
• 다시 돌아가서 해당 연결의 시작 노드를 보고 동일한 작업을 수행한다
  
  

• smallElement() 메소드는 가장 작은 costSoFar 값을 가진 리스트에서 NodeRecord를 반환
• contains(node) 메소드는 파라미터에 동일한 NodeRecord가 포함되면 true
• find(node) 메소드는 파라미터와 동일한 목록에서 NodeRecord를 반환

한계

• 가능한 한 최단 경로를 찾아 그래프 전체를 무차별적으로 검색합니다
• 가능한 모든 노드들에 최단 경로를 찾을 때 유용하지만 점에서 점 경로 찾기에는 낭비
• 생성된 경로보다 먼 경로여도 계속 찾음

A*

• 다익스트라처럼 다 찾아야 하는 알고리즘은 점 대 점 경로 찾기에서 비효율적이며 거의 사용 안 됨
• 다익스트라보다 덜 채우는 방식
• 다익스트라와 달리 A*는 그래프 이론에서 최단경로를 찾는 것이 아니라 점 대 점 경로 찾기용으로 설계됨

F = G + H
Estimated-total-cost = cost-so-far + heuristic

알고리즘

• 지금까지 가장 낮은 비용 값을 가진 개방형 노드를 항상 고려하는 대신 전체 경로가 가장 짧은 노드를 선택합니다
• 가능성이 가장 높은 개념은 heuristic

current Node

• 지금까지의 총 비용 저장
• 하나의 값을 더 저장: 시작 노드에서 현재 노드를 거쳐 목표로 가는 경로에 대한 총 비용 추정치
• 예상 총 비용: 지금까지의 비용과노드에서 목표까지의 (예상) 거리(=heuristic value)
  

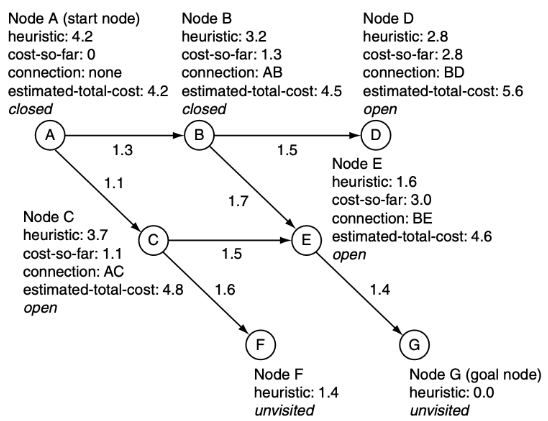
Node list

• 이전과 달리 최소 예상 총 비용을 가진 오픈 리스트에서 노드는 각 반복에서 선택됨
• 거의 항상 최소 총 비용을 가진 노드와 다름
• 이러한 변경을 통해 알고리즘은 노드의 총 추정 비용이 작은 경우 보다 유망한 노드를 조사할 수 있으며, 추정 비용이 상대적으로 짧고 추정 거리가 상대적으로 짧아야 목표에 도달할 수 있습니다. 추정 값이 정확한 경우 목표에 더 가까운 노드를 먼저 고려하여 가장 수익성이 높은 영역으로 탐색을 좁힐 수 있습니다

cost-so-far

• cost-so-far 값에 대해서만 수행된다(예측 총 비용이 아니라)
• 다익스트라와 달리 A* 알고리즘은 closed list에 있는 노드에 대한 더 나은 경로를 찾기 가능
• closed list에서 노드를 제거하고 open list로 배치 가능

종료 조건

• open list에 있는 최소 노드가 목표노드일 때 종료
• 많은 수의 A* 구현은 목표 노드가 오픈 리스트에서 가장 작을 때까지 기다리지 않고 처음 방문했을 때 대신 종료됩니다

다익스트라와 비교

• closed node가 closed list에서 업데이트 및 제거가 필요한지 확인하기 위해 추가 검사를 추가합니다
• 또한 휴리스틱 함수를 사용하여 노드의 추정 총 비용을 계산하기 위해 두 줄을 추가하고 이 정보를 유지하기 위해 NodeRecord 구조에 추가 필드를 추가합니다
• 노드가 이미 휴리스틱을 계산한 경우 해당 값은 노드가 업데이트가 필요할 때 재사용됩니다

Heuristic

• 휴리스틱이 정확할수록 A*의 충전량이 감소하고 실행 속도가 빨라집니다
• 휴리스틱을 0으로 설정하면 Dijkstra임(A*에서 가중치가 0인 경우)

heuristic 과소평가

• heuristic이 너무 작아서 실제 경로 길이를 과소평가할 경우 A* 실행하는 데 더 오랜 시간이 걸립니다.
• F = G + H 중 G에 편향될 것임(지금까지의 거리)
• 시작 노드와 가까운 노드 위주로 선호하게 됨
• Dijkstra와 별반 다를 게 없어짐

heuristic 과대평가

• F = G + H 중 H에 편향된다.
• 노드 간 경로 비용이 최소가 아니더라도 거쳐가는 노드가 적은 경로를 선호함

Euclidean Distance

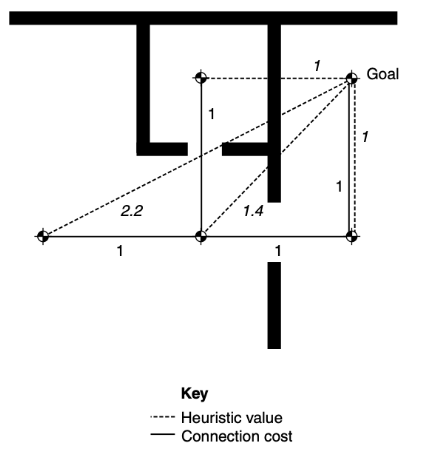
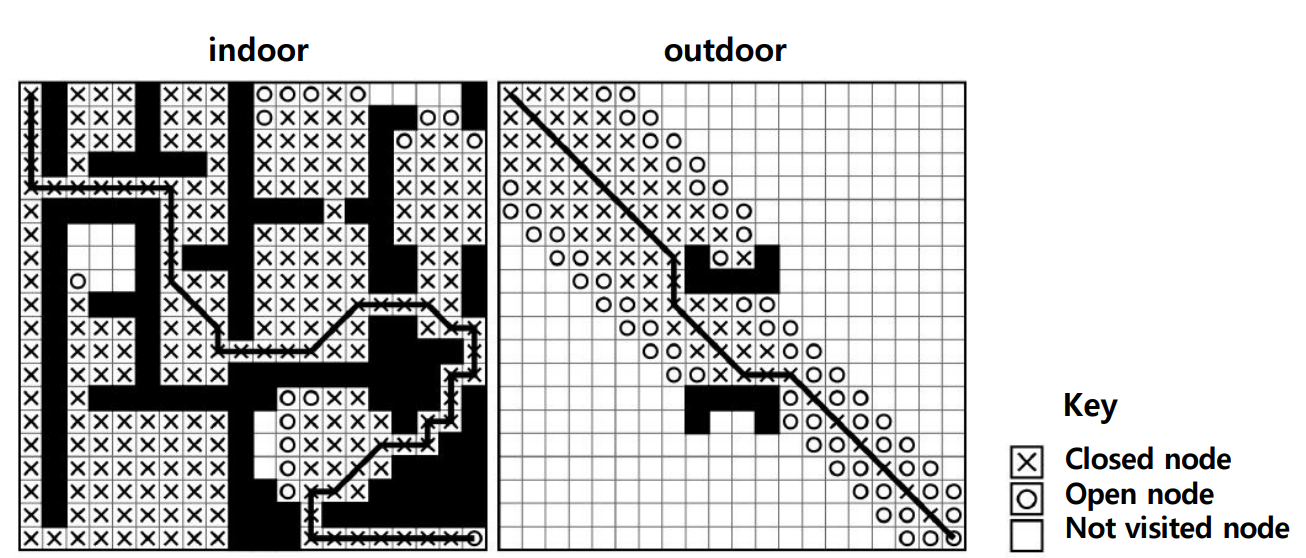
• 일반적으로 heuristic은 Euclidean Distance인데, 이거 사용하면 과소평가 당함.
• 유클리드 거리는 일직선임. 벽과 장애물 상관 안 함, 실제로 연결이 안 돼도 목표지점까지의 거리
• 유클리드 거리는 항상 정확하거나 과소평가된다
• 이동의 제약이 거의 없는 실외 환경에서는 유클리드 거리가 매우 정확하고 빠르다
• 유클리드 거리 휴리스틱을 사용하면 실내 레벨에선 가득 채우고 느림
• Outdoor에서는 적게 탐색하고 빠르다
  

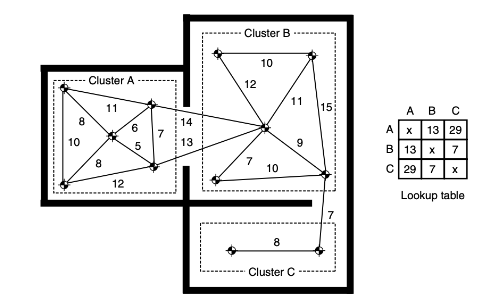
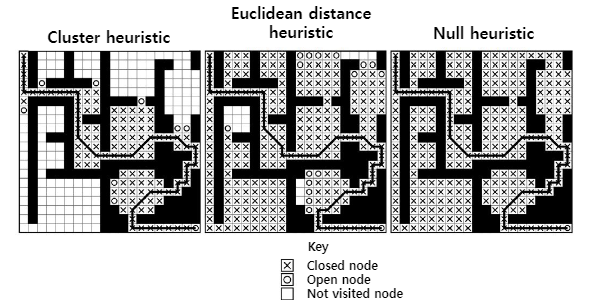
Cluster heuristic

• 클러스터 휴리스틱은 노드들을 클러스트 안에서 그룹화 함
• 그런 다음 각 클러스터 쌍 사이의 최단 경로를 제공하는 lookup table 생성. (여기까지 offline)
• 클러스터 휴리스틱은 유클리드 거리보다 실내 지역에서 경로 찾기 성능을 극적으로 향상시키는 경우가 많은데, 이는 겉으로 보기에는 가까운 위치를 연결하는 복잡한 경로를 고려함
• [주의]
  • 클러스터의 모든 노드에 동일한 휴리스틱 값이 주어지기 때문에 A* 알고리즘은 클러스터를 통해 최적의 경로를 쉽게 찾을 수 없음
  • 채우기 측면에서 볼 때, 알고리즘이 다음 클러스터로 이동하기 전에 클러스터가 거의 완전히 채워지는 경향이 있습니다
    • 클러스터 크기가 작으면 이는 문제가 되지 않고 휴리스틱의 정확도가 우수할 수 있습니다.
    • 반면 룩업 테이블이 클 것입니다(그리고 전처리 시간이 클 것입니다).
    • 클러스터 크기가 너무 크면 성능이 한계될 것이고, 간단한 휴리스틱이 더 나음.

Fill Patterns

• 클러스터 휴리스틱은 거의 채워지지 않는 반면, 제로 휴리스틱은 대부분 채운다
• 이것은 knowledge vs. search trade-off의 좋은 예시임
  
• 유클리드 거리는 약간의 지식을 제공합니다.(두 지점 간 이동 비용은 거리에 따라 다릅니다.) - 제로 휴리스틱은 지식이 없으며 많은 탐색이 필요합니다
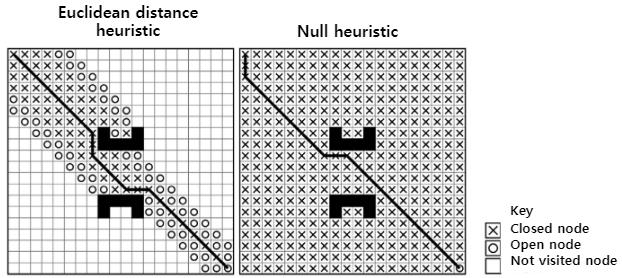
  • 즉, 아는 게 있으면 아는 대로 하고 아는 게 없으면 그만큼 탐색을 많이함
    
• 장애물이 적은 outdoor에서는 유클리드 거리가 훨씬 정확합니다
  • 유클리드 휴리스틱이 더 정확하고, 더 적게 채움

Trade-off

• 휴리스틱이 더 복잡하고 게임 레벨의 세부 사항에 맞춰진다면, A* 알고리즘은 탐색을 덜 해야 함(문제에 대한 많은 지식을 제공합니다)
• 이것의 궁극적인 확장은 궁극적인 지식을 가진 휴리스틱입니다: 완전히 정확한 추정치입니다
  • 즉, 추정치가 정확하면(= 아는 게 많으면) 탐색을 덜 하면서 효율적으로 탐색 가능함

Dijkstar is A*

• Dijkstra 알고리즘은 A* 알고리즘의 부분 집합입니다
• A*에서 휴리스틱 값을 cost-so-far까지 A* 에 추가하여 노드의 예측 총 비용을 계산
  • F = G+H
• 휴리스틱이 0인 경우 Dijkstra