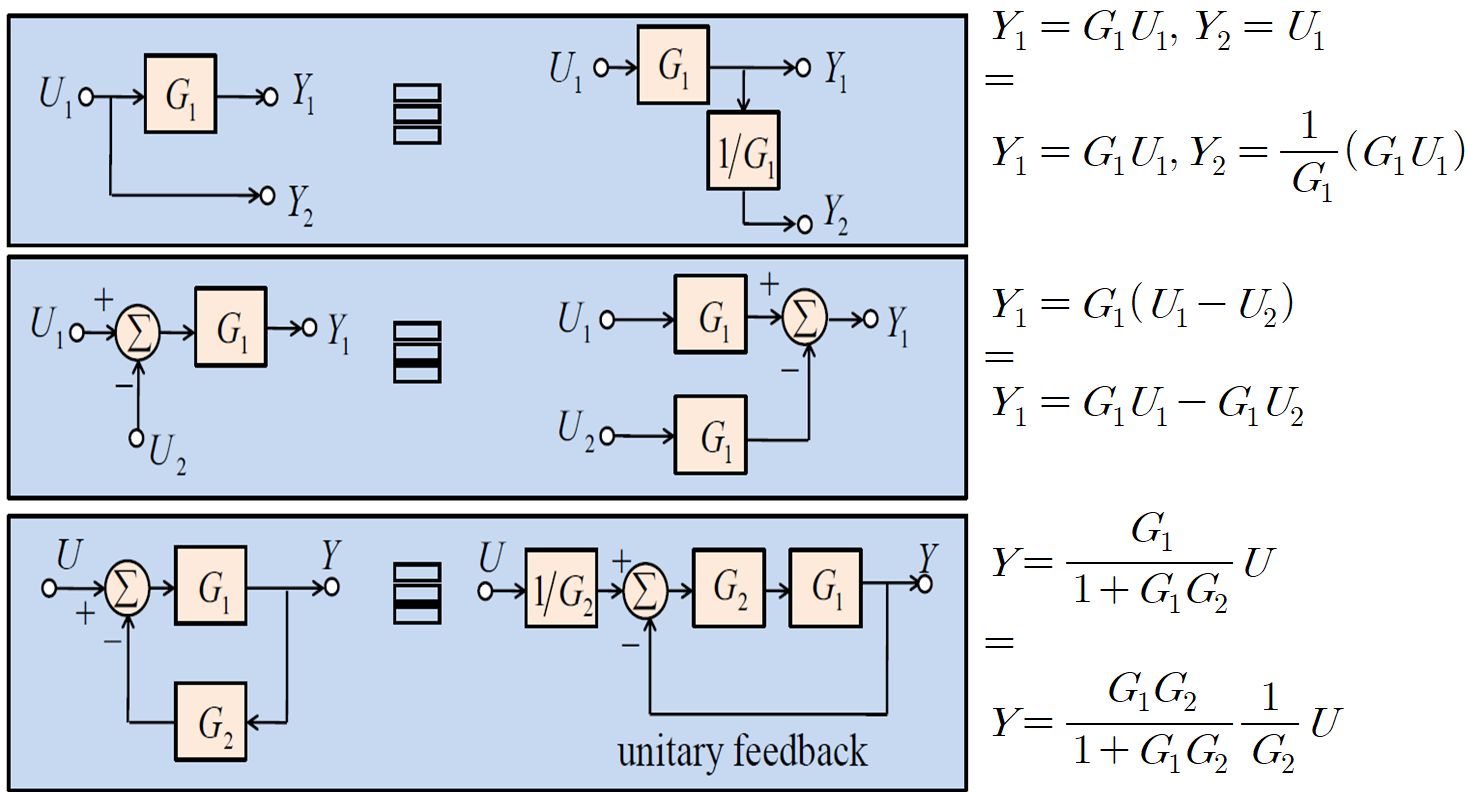
선형성의 특징
1. Homogeneity (동질성)
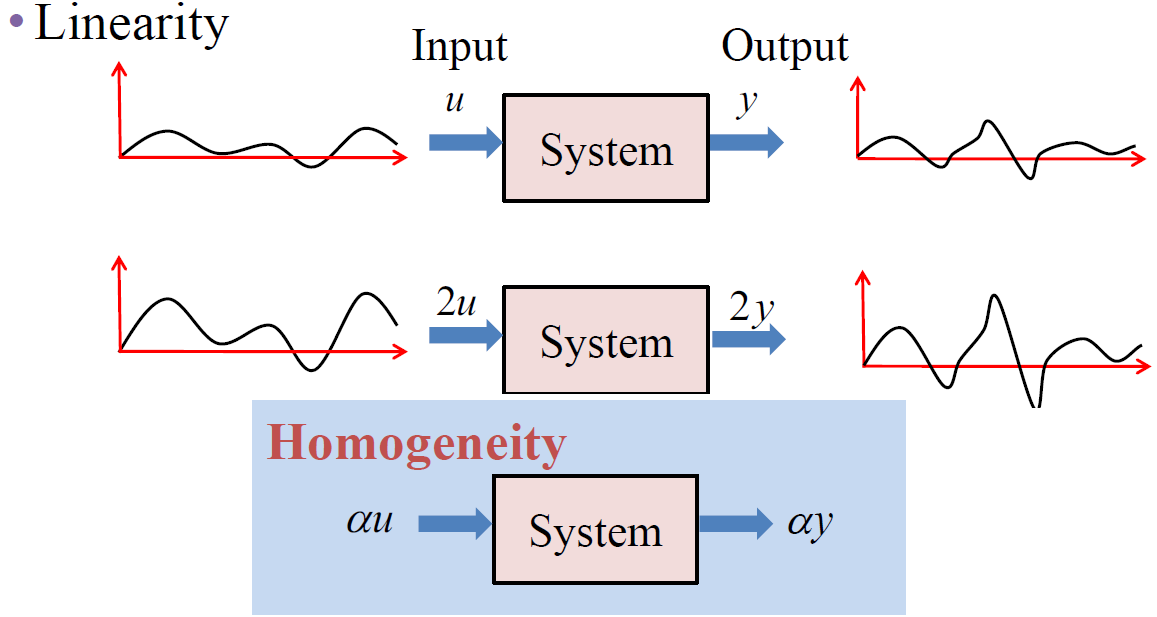
2. Additivity (가산성)
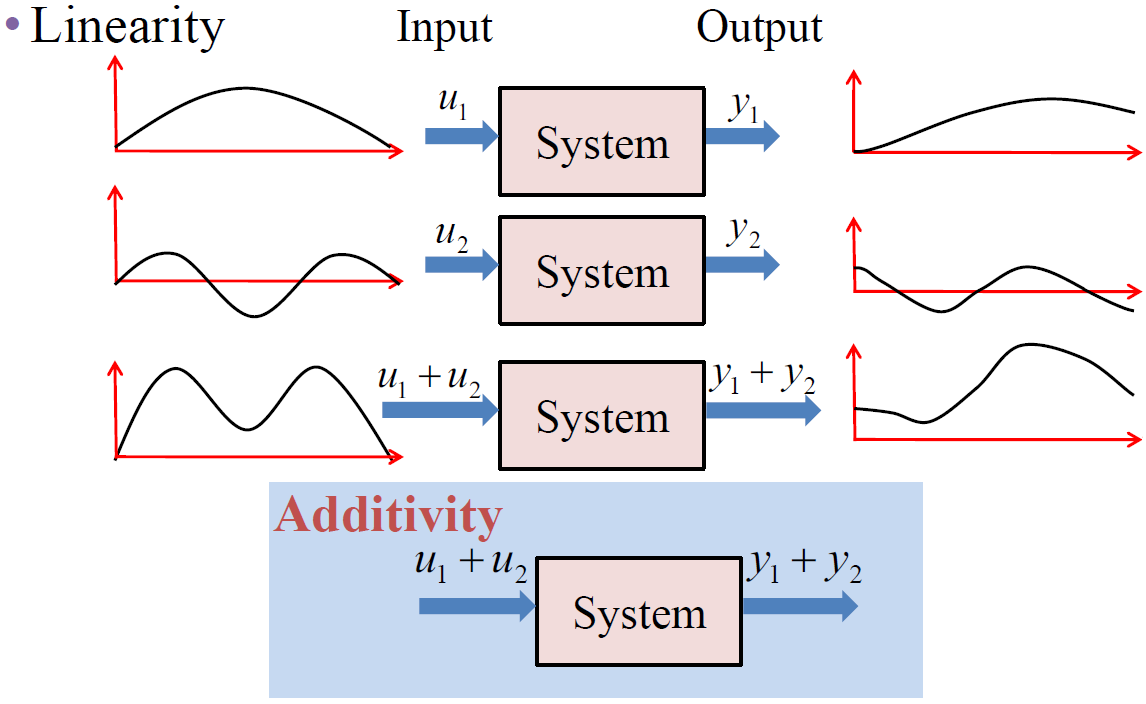
3. Superposition(중첩의 원리)
- Superposition = Homogeneity + Additivity
Time Invariance (시간 불변성)
- 입력 지연 -> 출력 지연, 양상은 그대로, 시간만 지연
- Input signal : u1, u2
- output : y1, y2
< Response by Convolution >
- short pulse : 단위 영역을 가지는 사각 pulse
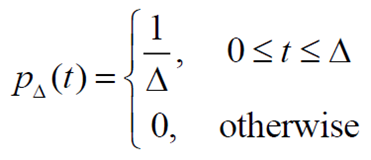
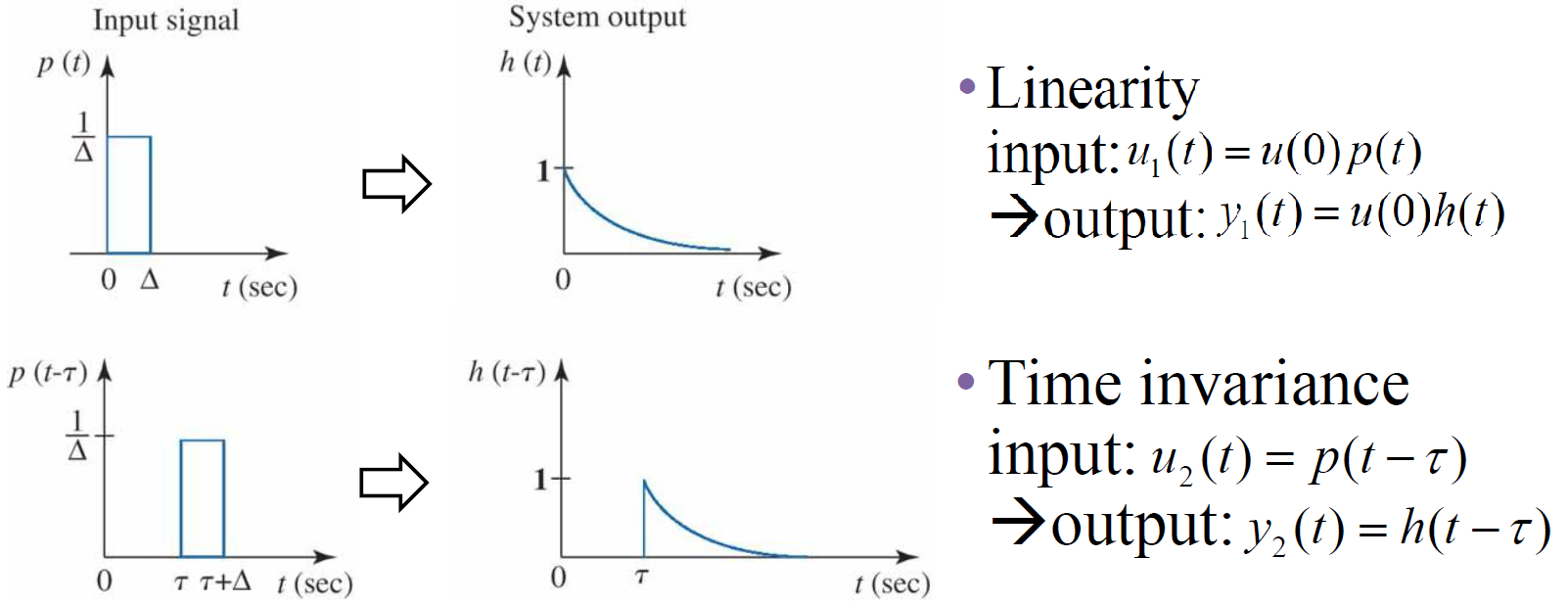
Response of pulse
1. 일반적인 펄스의 응답
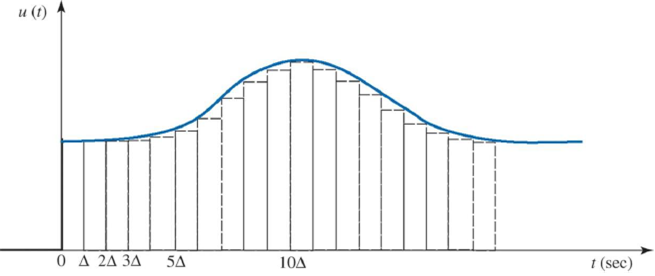
-
: 시간에 따라 변화
(unit pulse인 에 가 곱해져 입력 도출)- = =
-
입력 응답(출력)
- Homogeneity에 의해
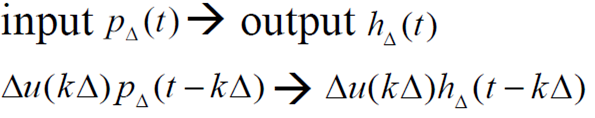
- Homogeneity에 의해
-
적분의 원리로 인해 ()
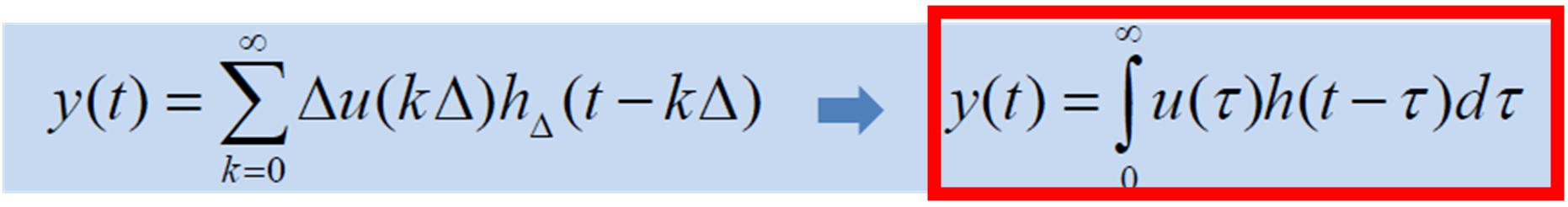
이것을 바탕으로 impulse 응답을 알아볼 것이다.
2. impulse 응답
- impulse : 아주 짧은 시간동안 시스템에 변화를 주는 입력 (넓이가 1)
- 시간이 0에 극한일 때 1
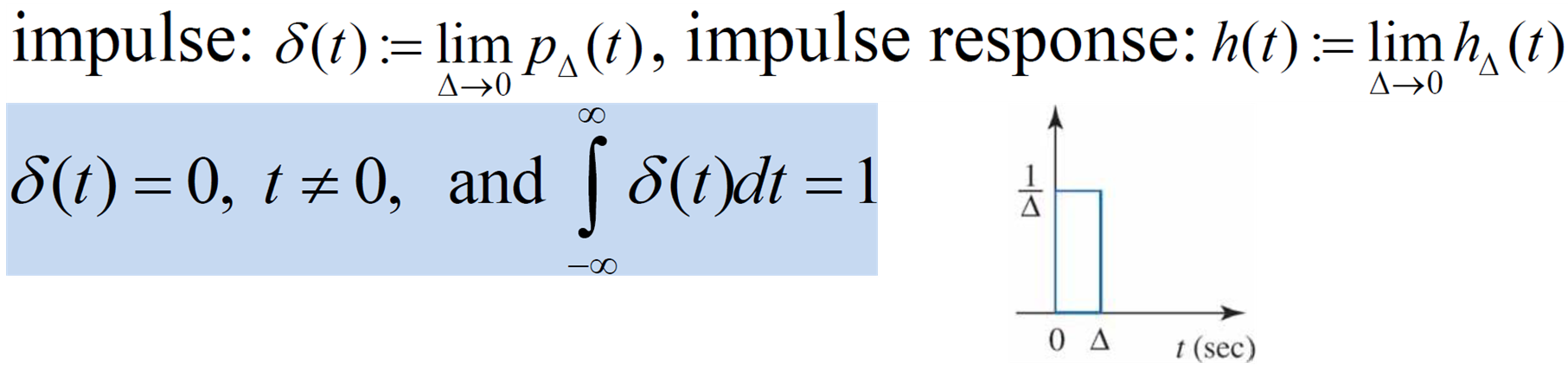
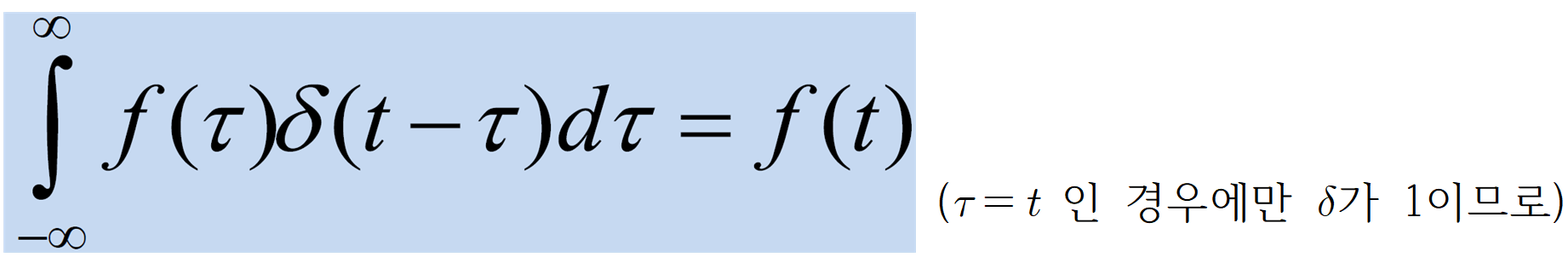
- 시간이 0에 극한일 때 1
이로인해
Convolution integral
-
이용
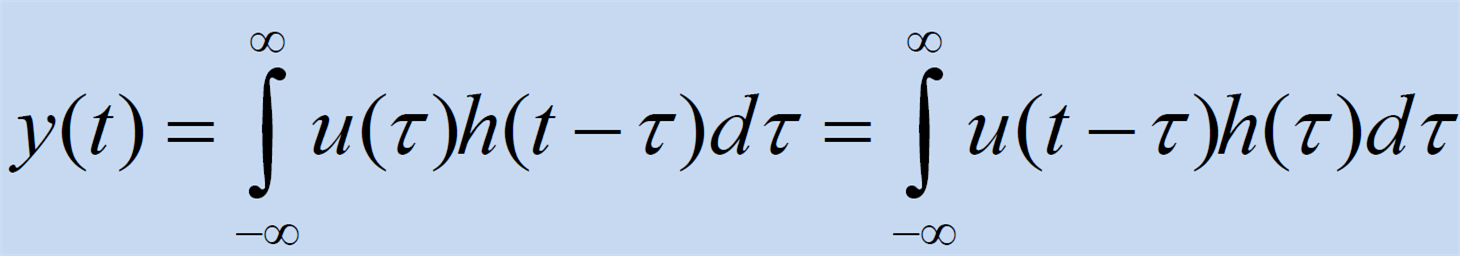
-
ex) , (impulse 가하기 전 : ) 인 경우 (0초일 때 impulse 입력)
- (impulse 가한 이후)
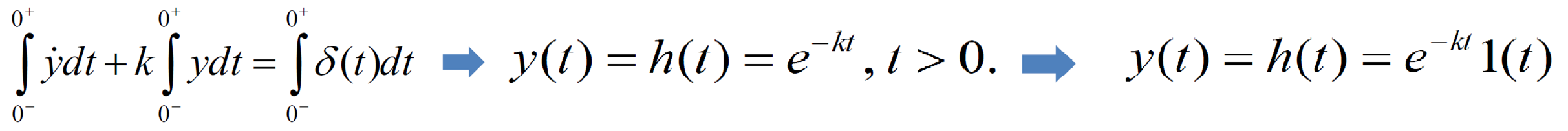
- (impulse 가한 이후)
일반적인 입력에 의한 응답 (0초부터 가해지는 입력)
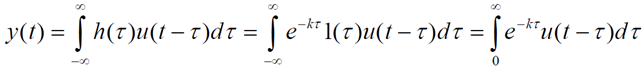
하지만 이런 식의 convolution integral은 계산이 복잡해서 라플라스 변환과 역변환으로 계산 할 것이다.
라플라스 변환

- 이제 라플라스 변환을 통해 응답을 다음과 같이 표현할 수 있다.
하지만 보통 시작을 0초로 두기 때문에 라플라스 변환 : 로 생각
1. 라플라스 변환표

2. 라플라스 변환 특성
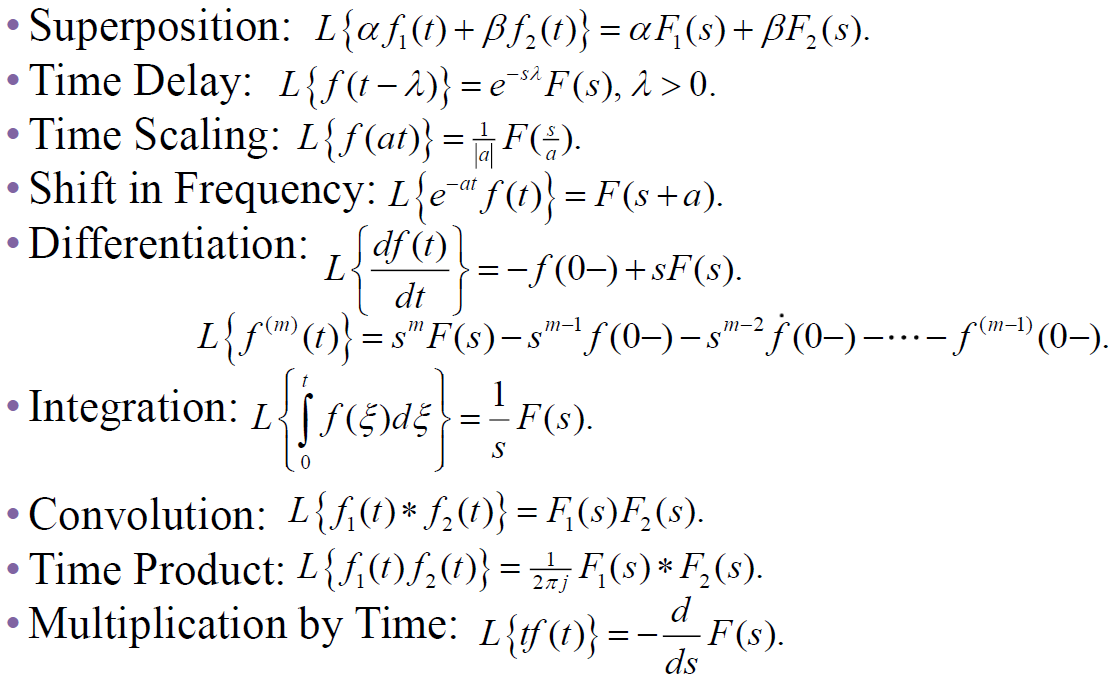
- 라플라스 역변환은 보통 부분분수로 분리하여 역변환이 쉬운 형태로 바꿔 진행
- 역변환을 통해 원하던 출력 도출
최종적으로 출력은 입력에 전달함수를 곱한 형태
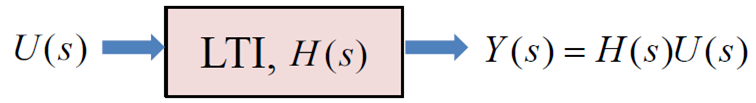
Final Value Theorem (최종값 정리)
- 최종상태가 특정 값으로 수렴하는 정상상태가 되는 시스템일 경우 최종 값을 쉽게 계산 가능
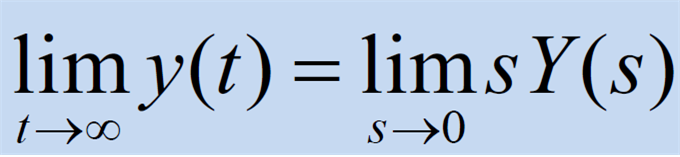
주파수 응답
- 사인파 입력을 시스템에 인가했을 때 나오는 진폭의 크기와 위상이 다른 같은 주파수의 파형 응답
- 최종 형태
- 부분을 에 대한 식으로 변환해 정리
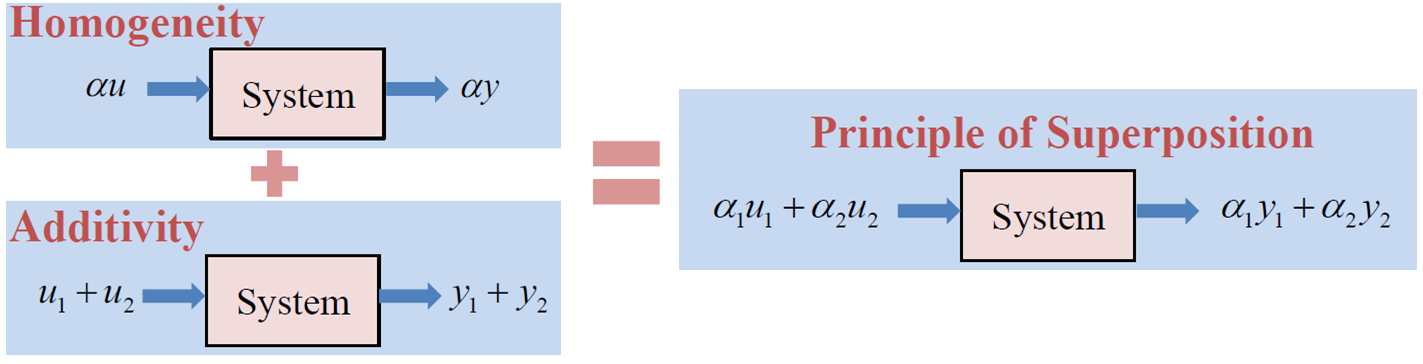
Block Diagram
- 시스템의 인과관계를 알기 쉽게 나타낼 수 있다.
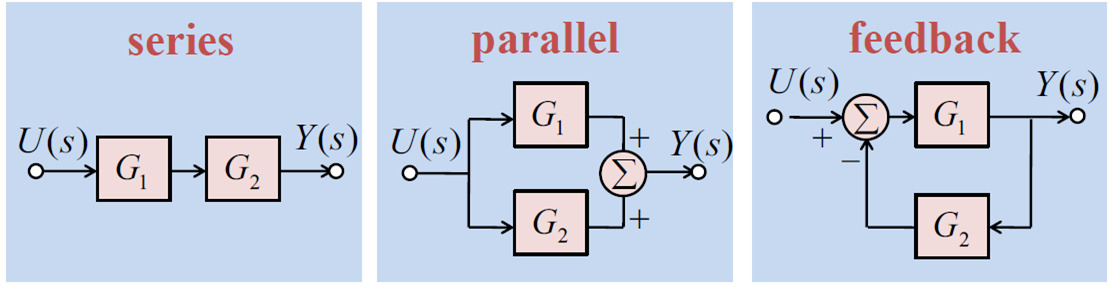
- 블록 다이어그램을 더 간단하게 만들 수 있다.