1. Pole & Zero

• Pole과 Zero는 시스템에 특성에 영향을 끼치는 요소
  • Pole : 전달함수의 분모를 0으로 만드는 극점, 이로 인해 시스템이 어떤 파형들로 구성되어있는지 알 수 있으며 시스템의 안정성과 관련
  • Zero : 전달함수의 분자를 0으로 만드는 극점, 시스템의 과도 응답 정도에 관련

ex) First order pole

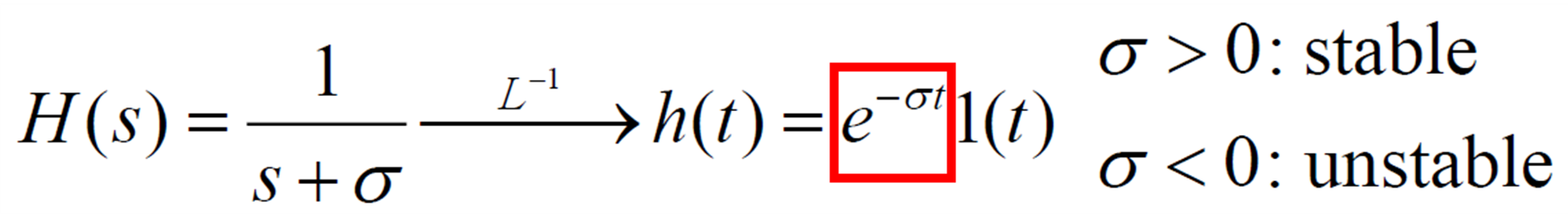
2. 복소수 pole

감쇠비의 기능을 알기위해 감쇠비 $\xi$ 값에 따른 Impulse response와 step response에 대해 알아 볼 것이다. (natural frequency $\omega_{n}=1$)

2-1. Impulse Response

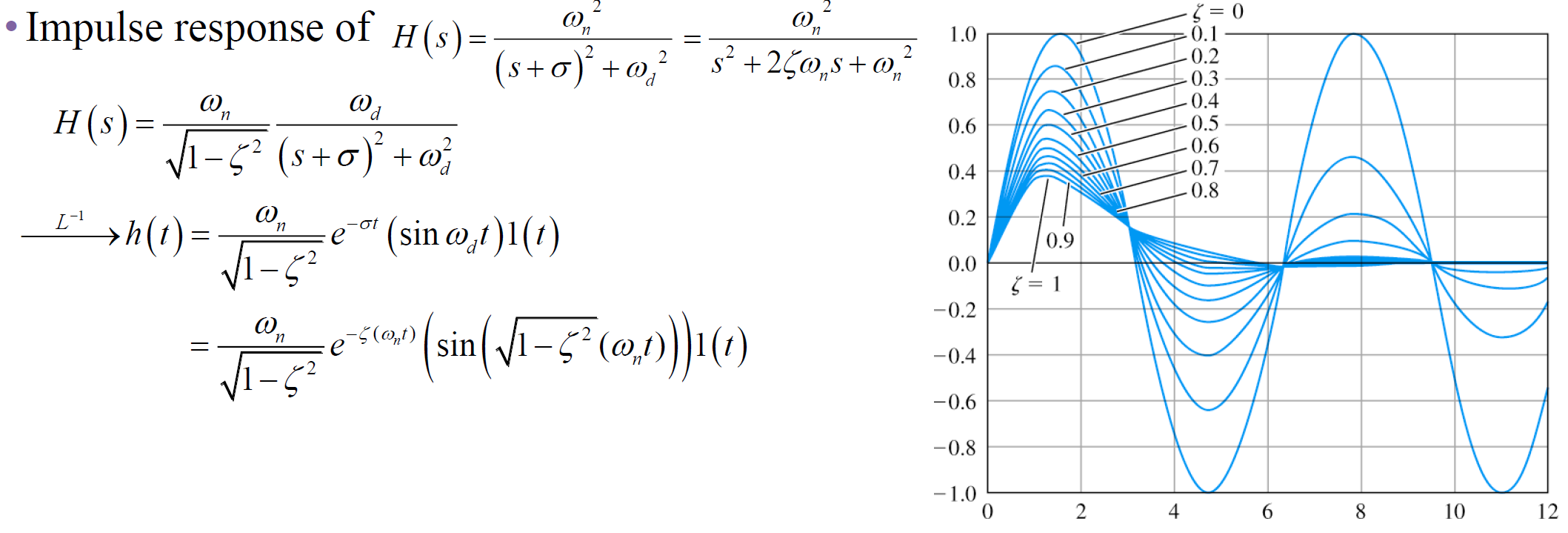
2-2. Step Response

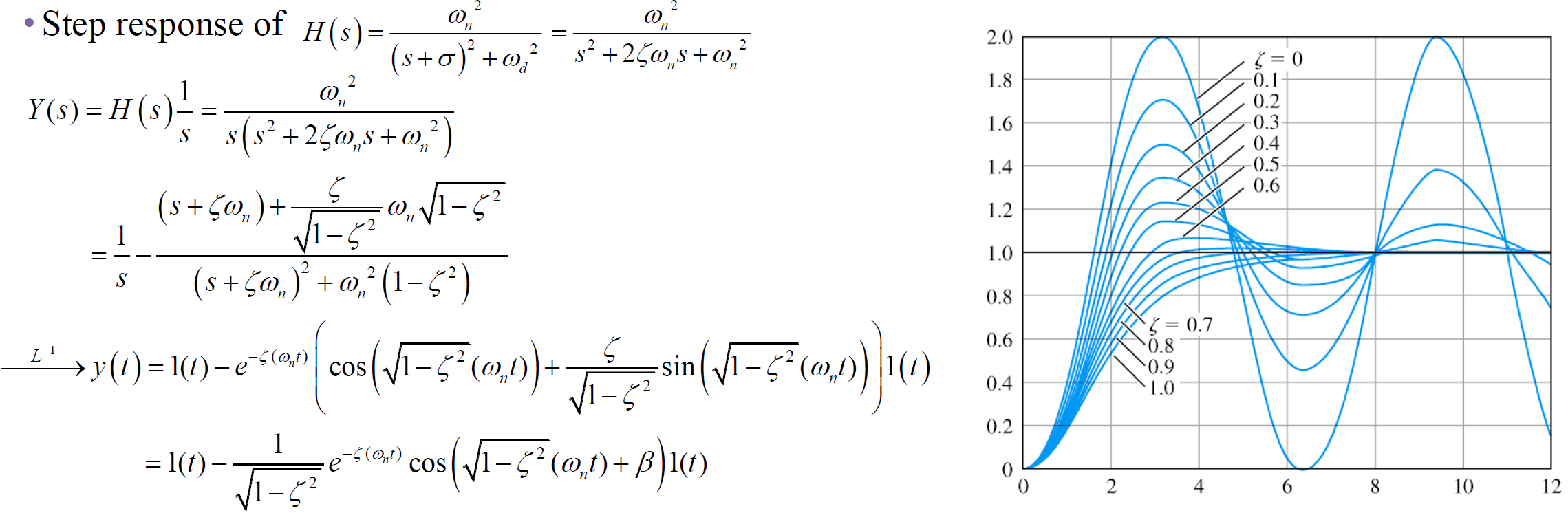
이를 통해 감쇠비가 클수록 파형이 작아지는 것을 확인 가능

3. $\sigma$의 부호에 따른 시스템 안정도

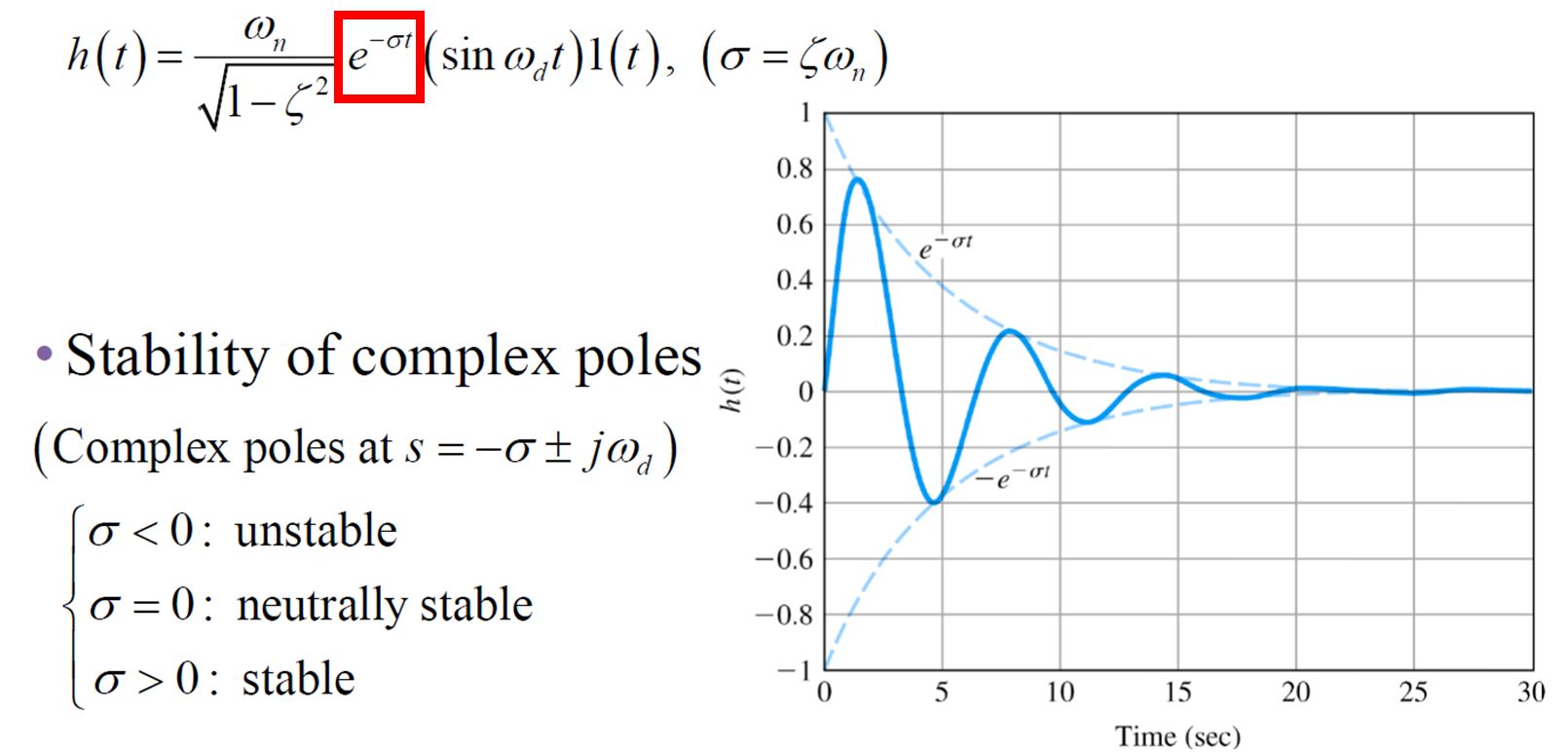
4. Pole의 위치에 따른 안정도

• pole이 복소수일 때 $\sigma$이 양수인지 음수인지에 따라 시스템의 안정한 정도를 알았기 때문에 pole의 위치에 따른 시스템의 안정도를 다음과 같이 표현 가능
  

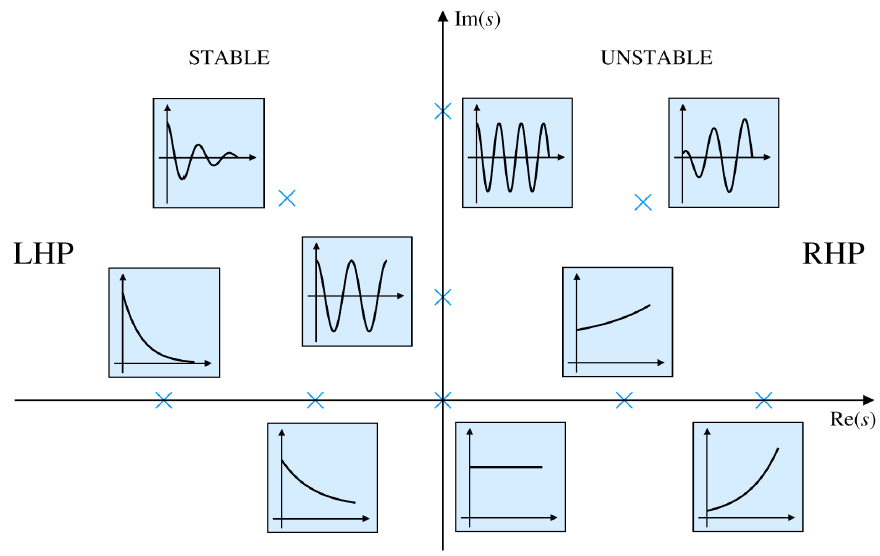
현실에서 보는 것처럼 시간영역에서 시스템의 응답을 살펴보기 위해 시간영역과 복소평면 상의 pole의 관계를 알아 보려한다.

5. 시간영역에서의 시스템 설계

• 2차 시스템의 step response 기준
  • Rise time (상승시간) : 목표 지점에 90%정도로 인접하는 시간
  • Overshoot (Maximum Overshoot) : 목표 값보다 넘어서는 최고 값
  • Peak time : Overshoot가 발생하는 시간
  • Settling time : overshoot이 특정 범위로 작아지는 시간

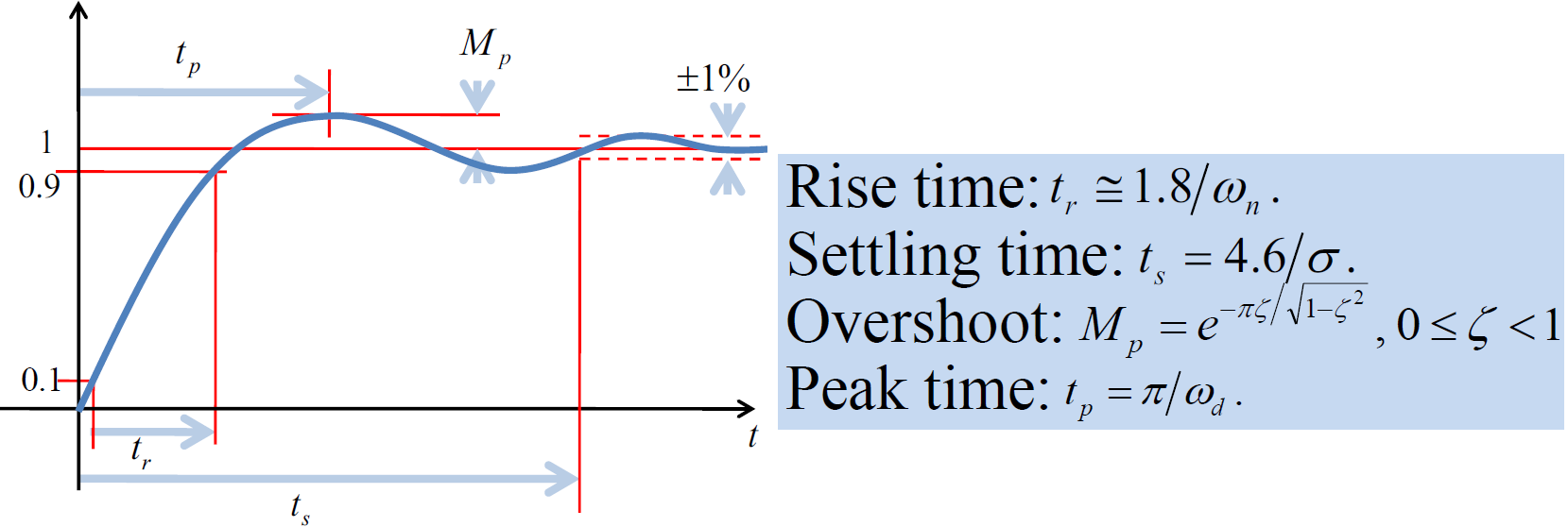
5-1. 감쇠비와 overshoot와의 관계

• 이름으로 알 수 있듯이 둘은 서로 반비례 관계

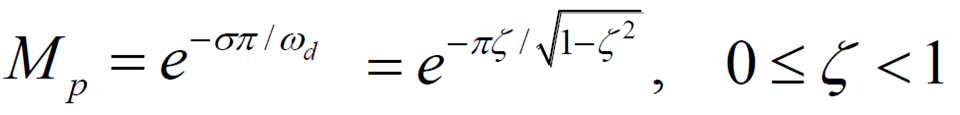
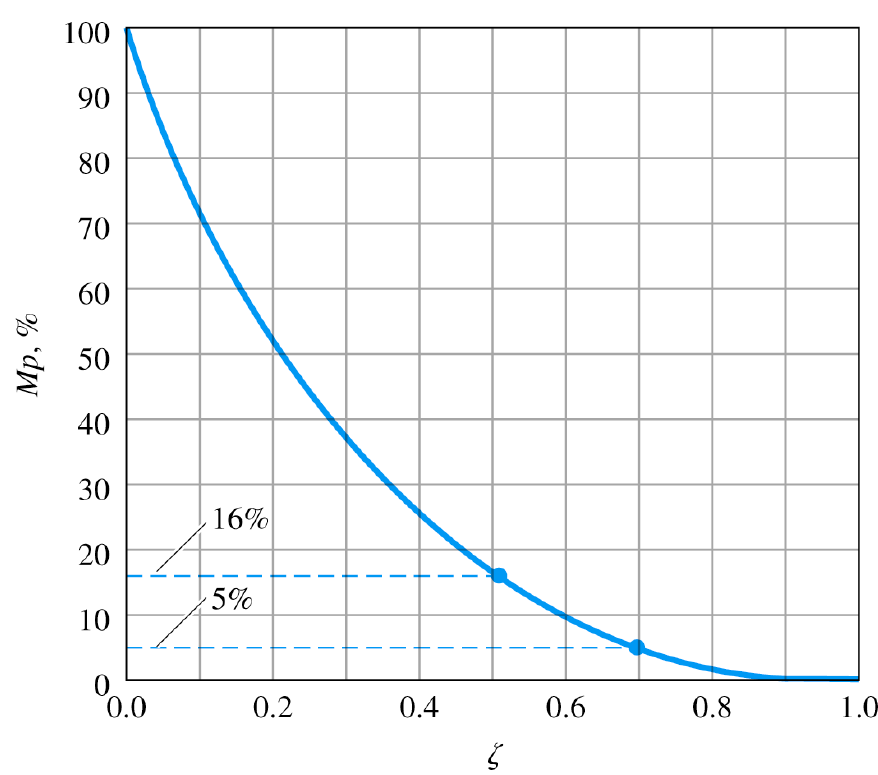
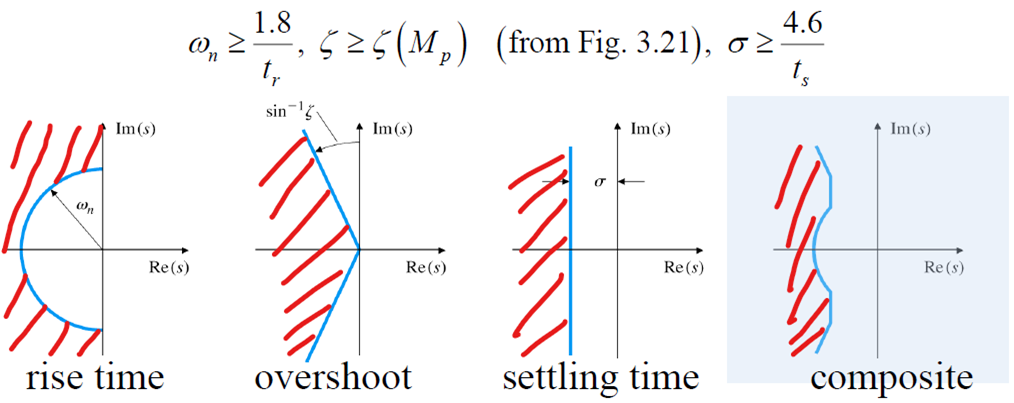
5-2. Pole 위치 범위

• 원하는 스펙에 따른 복소평면 위의 pole의 위치의 범위 특정 가능
  • Maximum overshoot가 특정 값 이하가 되기 위해선 감쇠비 $\xi$ 가 특정 값 이상

ex)

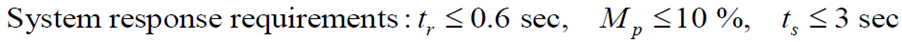
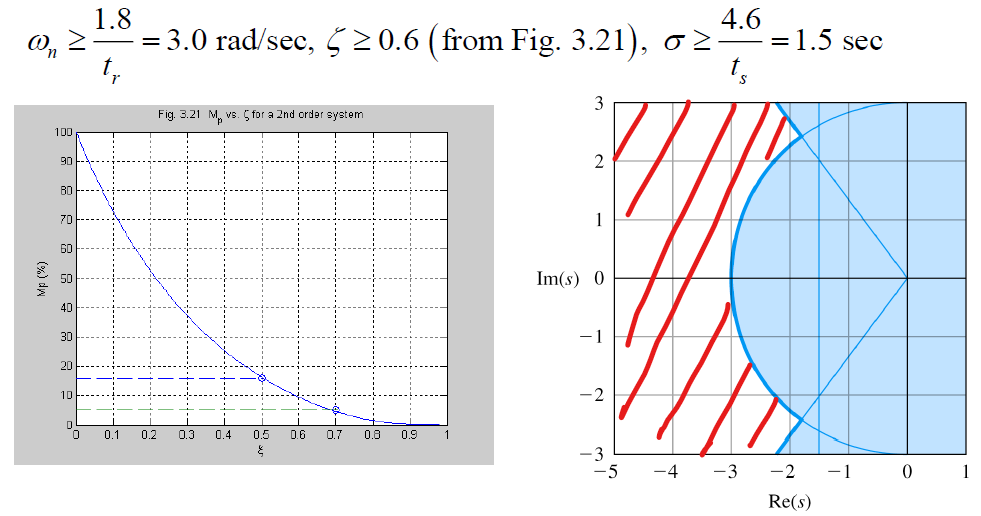
$\Rightarrow$ pole이 빨간 범위에 속해있어야 원하는 스펙에 만족

이렇게 해서 시스템의 스펙이 마음에 들지 않는다면 { ex) rise time이 너무 커서 목표 도달 오래 걸림, overshoot가 너무 큼, 수렴하기까지 너무 오래 걸림 } $\omega_{n}, \xi, \sigma$ 을 조정하여 스펙을 조정 가능

$\Rightarrow$ 이를 통해 시간영역과 복소평면과의 관계를 파악 가능

5-3. 시스템 속 zero의 영향

• zero가 pole에 가까이 위치하면 그 pole은 시스템에 영향 미미 (같아지면 서로 상쇄되어 없어진다는 걸 생각)

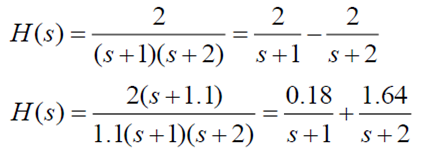
• 위의 식을 보면 두 번째 식에선 zero와 가까운 pole에 의한 파형은 계수가 매우 작아 시스템에 영향을 거의 주지 못할 것을 파악 가능

ex) 복소수에 대한 2차 시스템
$H(s)=\frac{(s/\alpha\xi\omega_{n})+1}{(s/\omega_{n})^2+2\xi(s/\omega_{n})+1} = \frac{\omega_{n}^2}{\alpha\xi\omega_{n}}\frac{s+\alpha\xi\omega_{n}}{s^2+2\xi\omega_{n}+\omega_{n}^2}$

• zero = $-\alpha\xi\omega_{n}=-\alpha\sigma$
• pole = $-\sigma+\omega_{d},-\sigma-\omega_{d}$
  $\Rightarrow \alpha=1$이면 실수 축 상 zero와 pole이 같아 pole과 zero 가까움

이를 $\alpha$값에 따른 step response를 그래프를 통해 파악 가능

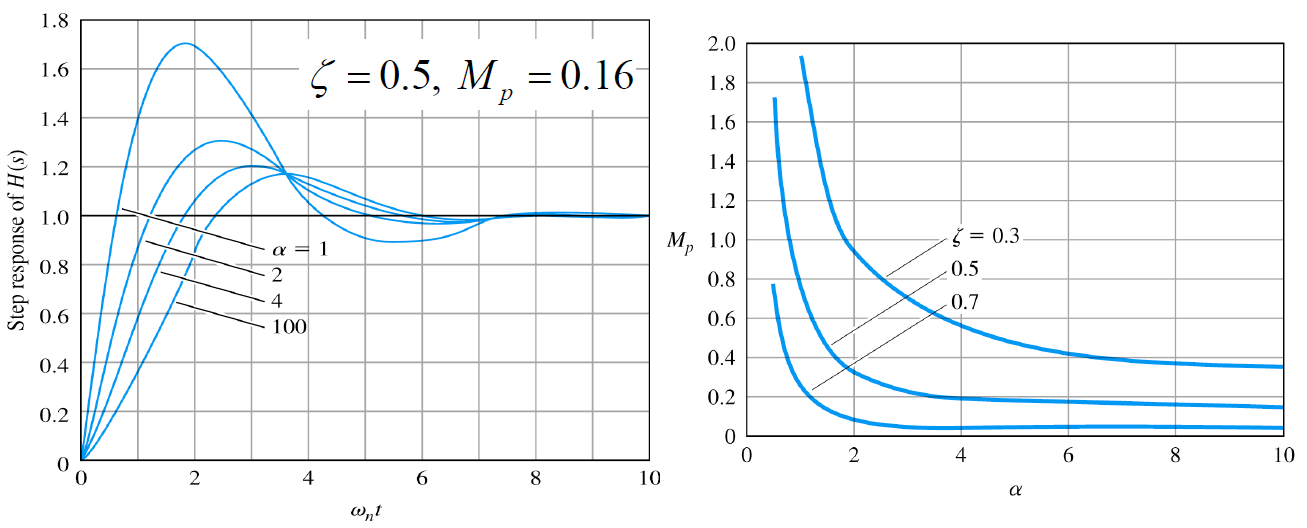
$\Rightarrow \alpha=1$ 즉 pole과 zero가 가까우면 overshoot가 매우 커지고 $\alpha$값이 커질수록 pole과 zero가 멀어지면 overshoot가 낮아지는 것을 확인 가능

5-4. 시스템 속 추가적인 pole의 영향

$H(s)=\frac{1}{[(s/\alpha\xi\omega_{n})+1][(s/\omega_{n})^2+2\xi(s/\omega_{n})+1]} = \alpha\xi\omega_{n}\omega_{n}^2\frac{1}{(s+\alpha\xi\omega_{n})(s^2+2\xi\omega_{n}+\omega_{n}^2)}$

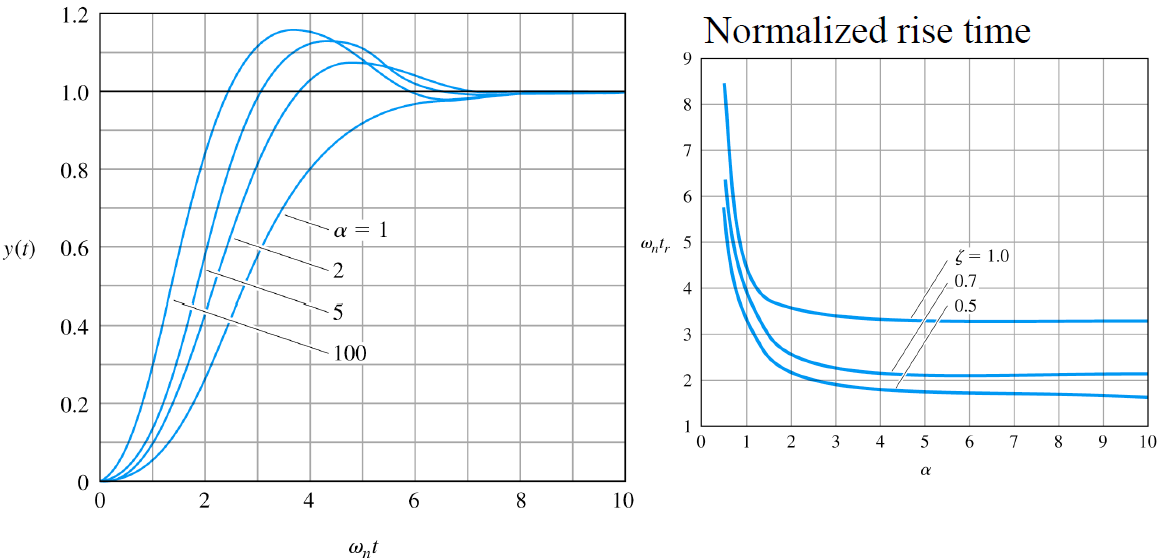
• pole = $-\sigma+\omega_{d},-\sigma-\omega_{d}, -\alpha\xi\omega_{n}=-\alpha\sigma$

• 마찬가지로 $\alpha$가 1이면 기존 2개의 pole과 가까운 pole이 추가되며 가까울 수록 overshoot가 줄어들어 안정적이게 되지만 rise time이 늘어나는 것을 확인 가능

  • 시스템의 최종상태에는 영향 x

6. 시스템의 안정성

• 안정성은 이름으로 알 수 있듯이 제어에서 가장 중요한 부분 중 하나
• pole 위치에 따른 시스템 안정도
  • 실수부가 음수면 stable
  • 실수부가 양수 혹은 0이면 unstable
  • 허수축에 중근 아닌 pole 존재 => 진동
  • 허수축에 중근인 pole 존재 => 발산
• 특성 방정식의 모든 계수가 양수면 pole이 다 음수 $\rightarrow$ 시스템 안정
• 낮은 차수의 경우 직접 pole이 음수인지 양수인지 판별할 수 있지만 높은 차수면 사실상 불가능

$\Rightarrow$ 안정성을 판별하는 방법으로 Routh’s Stability Criterion 사용

7. Routh’s Stability Criterion

• 시스템의 안정성은 pole에 의해 결정되므로 시스템의 분모의 특성방정식을 사용

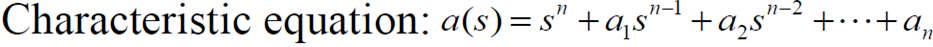
• Routh array의 첫 번째 열의 모든 값이 양수면 시스템이 안정
• 첫 번째 열의 값들의 부호가 바뀐 횟수 = RHP에 있는 pole개수