1. Tracking

• 원하는 시간에 출력이 레퍼런스 입력을 잘 따라 가는 것
• controller : 분모 차수 >= 분자차수 (분자 차수가 더 커지면 미분형태가 되는데 미분을 피하기 위해)
• controller가 plant를 cancellation되게 하는 경우는 지양

$\Rightarrow$ 출력이 레퍼런스 입력을 잘 따라가는 closed-loop 에 관심을 둘 것이다.

1-1. System Type, Reference tracking (외란, 노이즈 고려 x)

• 정상상태일 때 일정한 오차가 있도록 출력이 레퍼런스 입력을 따라가는 정도
• Type n 시스템 : $L(GD_{cl})$이 원점에 존재하는 pole을 n개 가짐
  $E=\frac{1}{1+L}R=SR,\quad (W=V=0)$

$\rightarrow$   Type n 시스템의 ess는 다음과 같다.

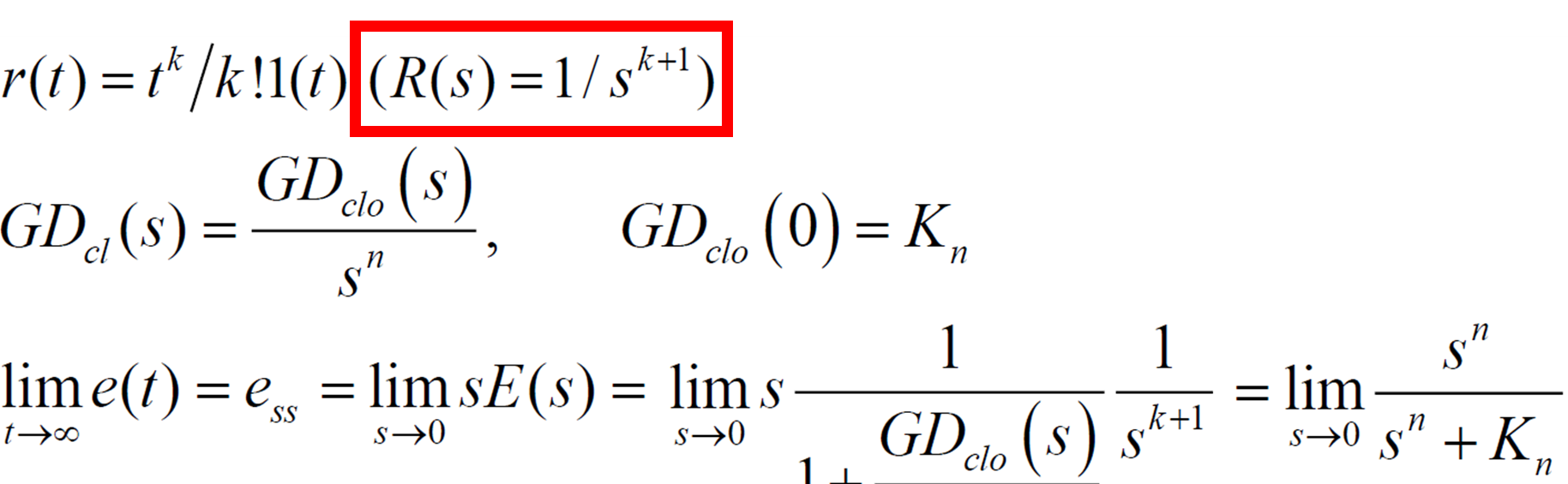
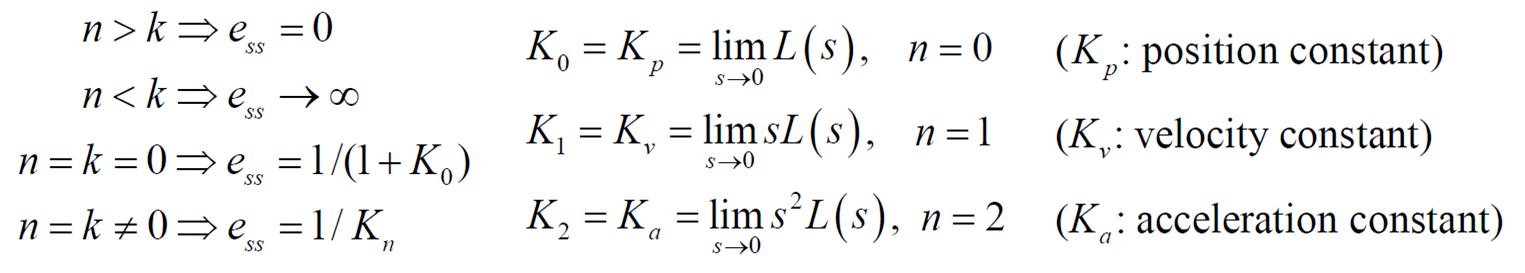
$\Rightarrow$ Type n 시스템에서 n이 입력 $t^k$의 $k$보다 크면 ess는 0, 같으면 특정 오차 값, 작으면 $\infin$
그래서 정리하면 다음과 같다.

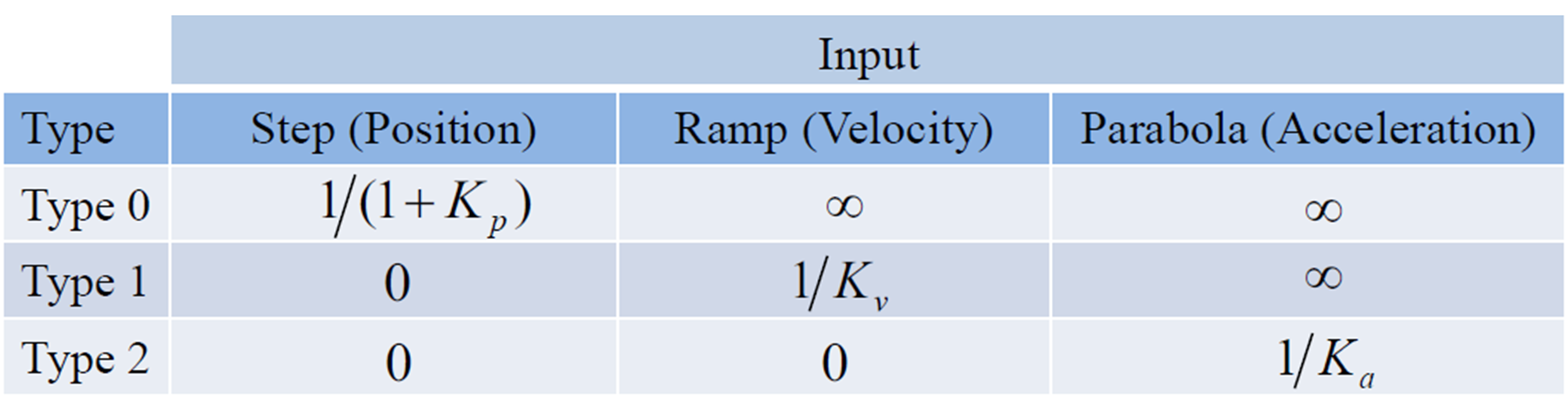
ex) Speed control(입력 = $t^1$) with PI control, $(W=0, V=0)$

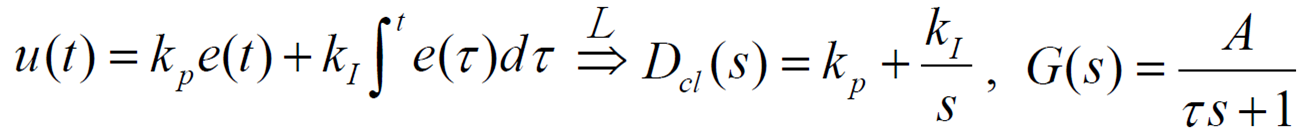
$\Rightarrow L(s)=G(s)D_{cl}(s)=\frac{A(k_ps+k_I)}{s(\tau s+1)}$,  원점 pole : 1개 $\rightarrow$ n=1

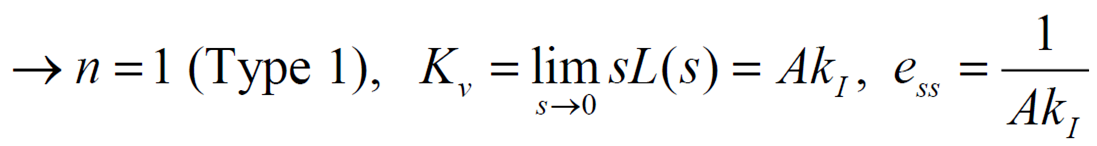
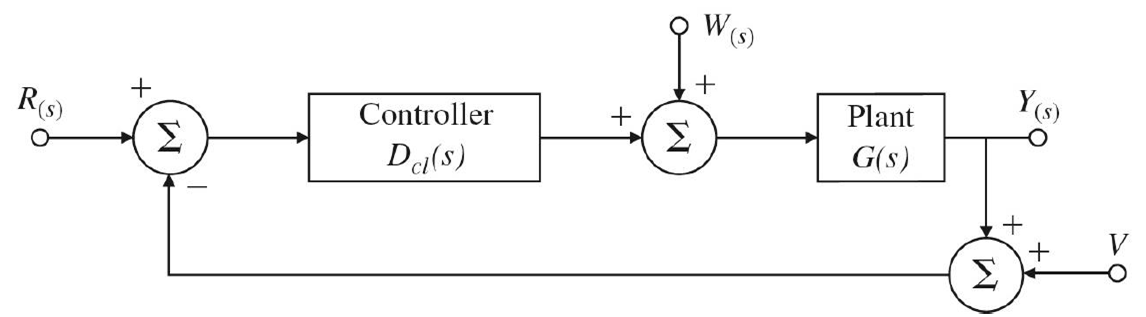
1-2. System Type, Disturbance Rejection (레퍼런스 입력, 노이즈고려 x)

• 외란만 들어왔을 때 시스템이 어떻게 반응할 것인가
• Reference tracking과 달리 $D_{cl}$(제어기)의 원점 pole의 개수만 중요

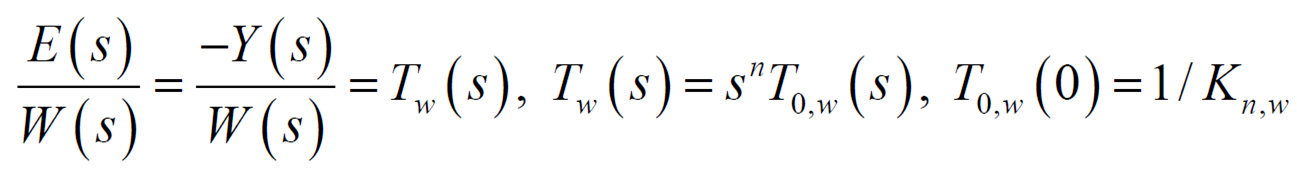
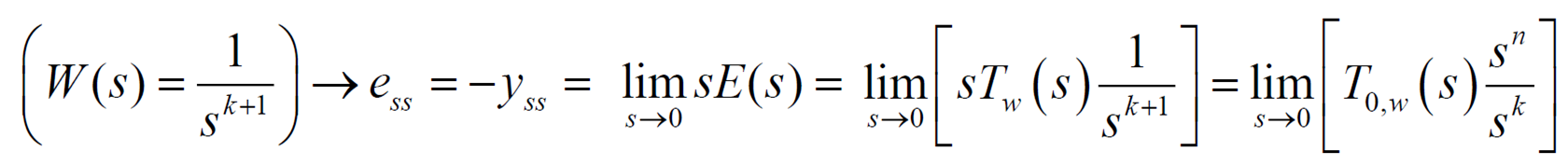
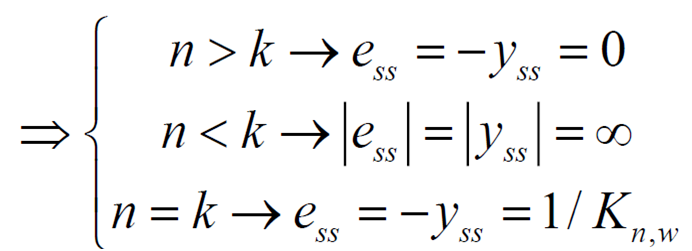
$\Rightarrow$ Reference Tracking과 유사함을 알 수 있다.

ex) PI control (k=1)

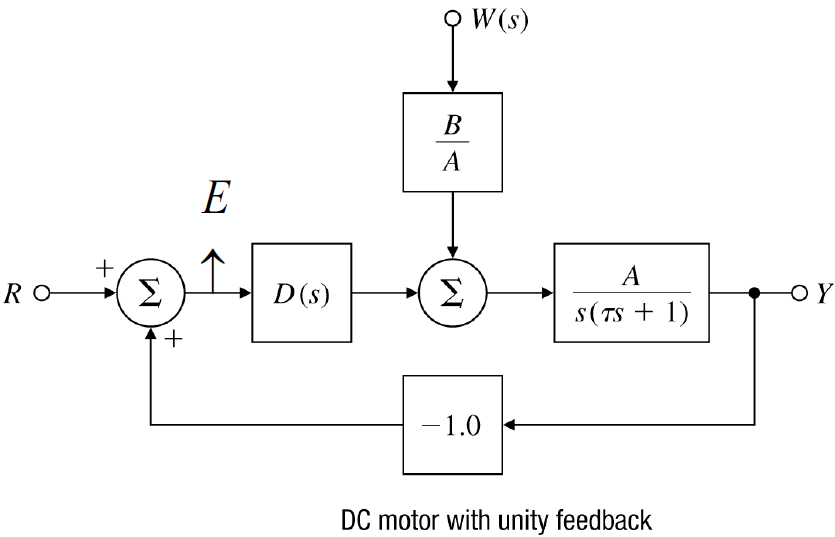
• PI control : $D(s)=k_p\ +\ \frac{k_I}{s}$

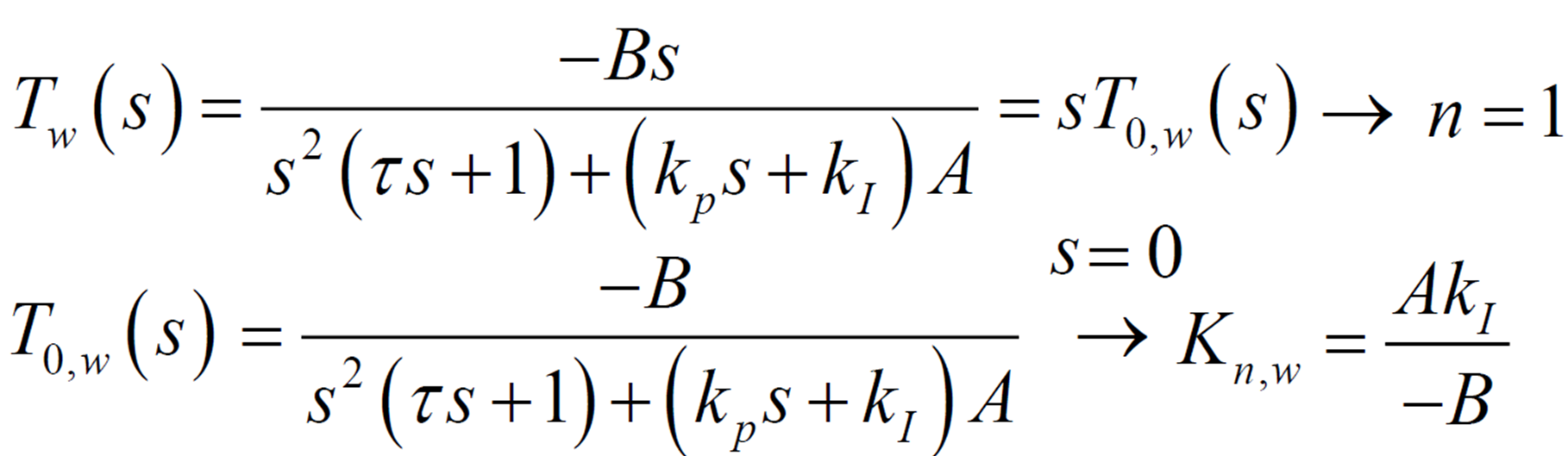
2. PID 제어기

• 비례(P), 적분(I), 미분(D) 텀을 사용한 제어기
• P : 현재 error가 큰지 작은지
• I : 현재 error가 얼마나 누적되었는지
• D : error가 점점 커지는지 작아지는지

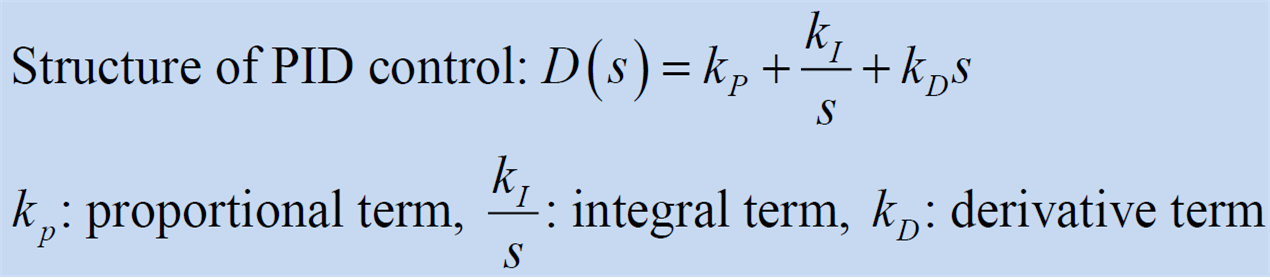
2-1. P control

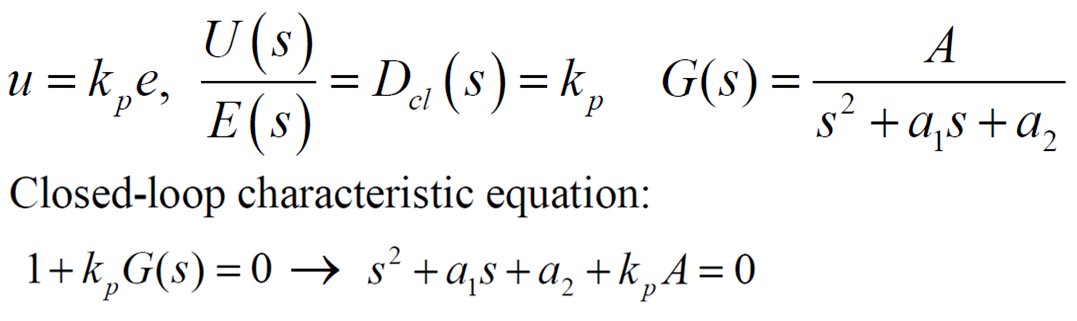
$k_p\uparrow\quad \rightarrow\omega_n=\sqrt{a_2+k_pA}\uparrow \quad \rightarrow\xi=\frac{a_1}{2\omega_n}\downarrow\quad \Rightarrow$ rise time $\uparrow$, 진폭 $\uparrow$

ex) speed control with the second order plant

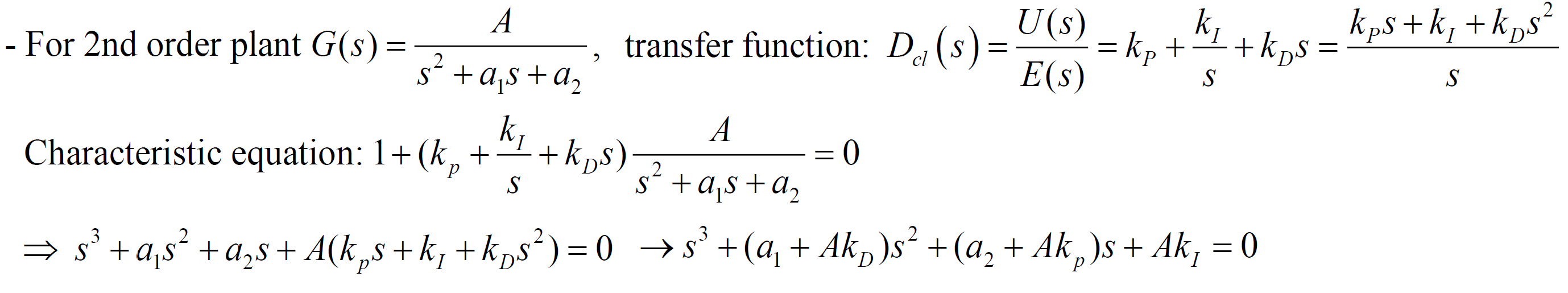
$\Rightarrow k_p, k_I, k_D$로 특성방정식의 계수 조절 가능해 pole 위치 제어 가능

2-2. Ziegler-Nichols Tuning of the PID controller

• 일반적인 상황에서는 모델 모름 -> Gain 설정 문제
  $\Rightarrow$ Ziegler-Nichols Tuning이 적절한 Gain 추천 : 가이드라인

2-2-1. 첫 번째 방법

• step response를 통해 $t_d, R$ 도출$(\xi=0.21)$

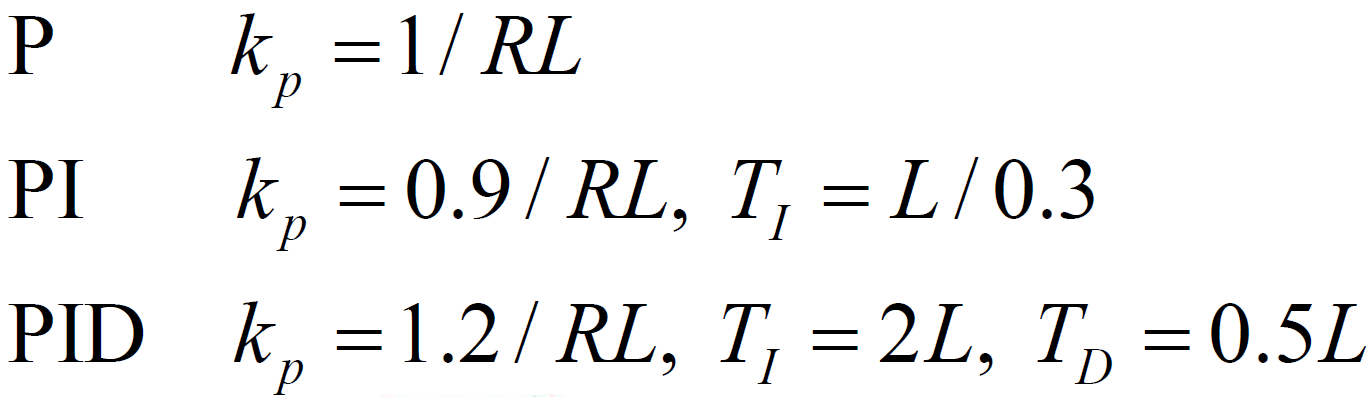
$\Rightarrow$ $t_d, R$을 통해 $k_p, k_I, k_D$값 쉽게 구하는 것 가능

2-2-2. 두 번째 방법 (Ultimate sensitivity method)

• 시스템의 P gain 높아져 불안정해질 때 적합
• $K_u$ : Ultimate gain, 시스템이 불안정(진동)하기 시작하는 P gain
• $P_u$ : Ultimate period, 시스템이 불안정하기 시작할 때의 출력 진동의 주기

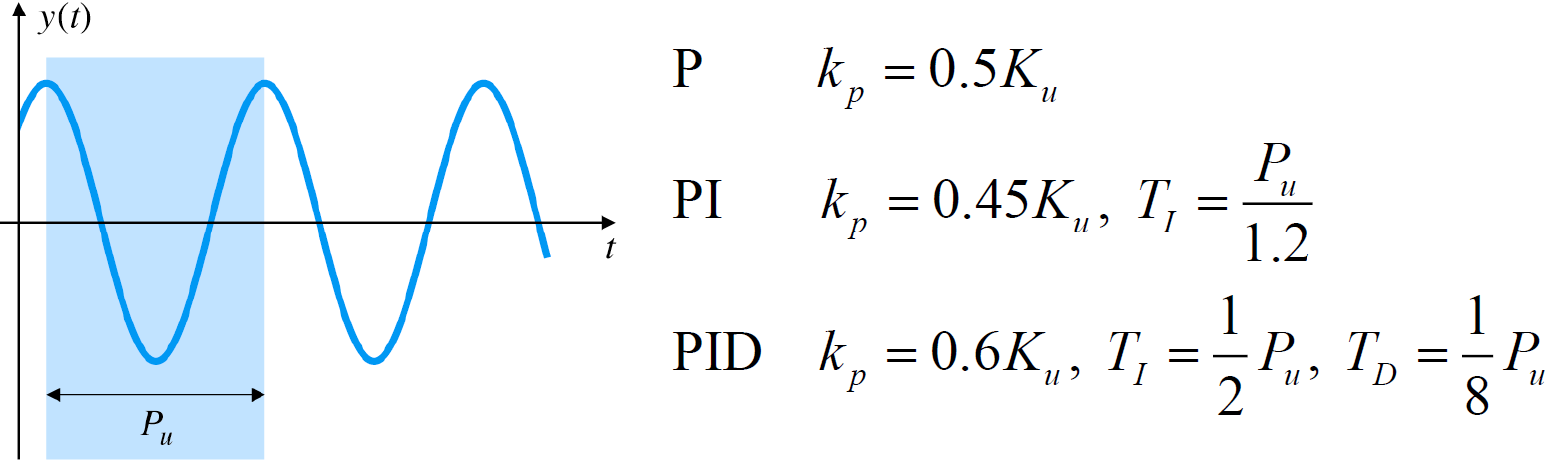
$\Rightarrow K_u, P_u$를 통해 $k_p, k_I, k_D$ 값 쉽게 구하는 것 가능