1. 제어의 4가지 쟁점

• stability(안정성) : 시스템이 입출력 간의 관계에서 안정한 가
• Tracking : 출력이 기준 입력을 잘 쫓아가는 가
• Regulation : 상수 기준 입력이 들어왔을 때 외란이 있어도 출력이 상수로 나오는 가
  • disturbance rejection : 외란에 대한 영향을 최대한 줄이는 것
• Sensitivity : 시스템이 바뀔 때 전달함수가 어떻게 바뀌는 가

2. Open-loop control vs Closed-loop control

2-1. Open-loop control system

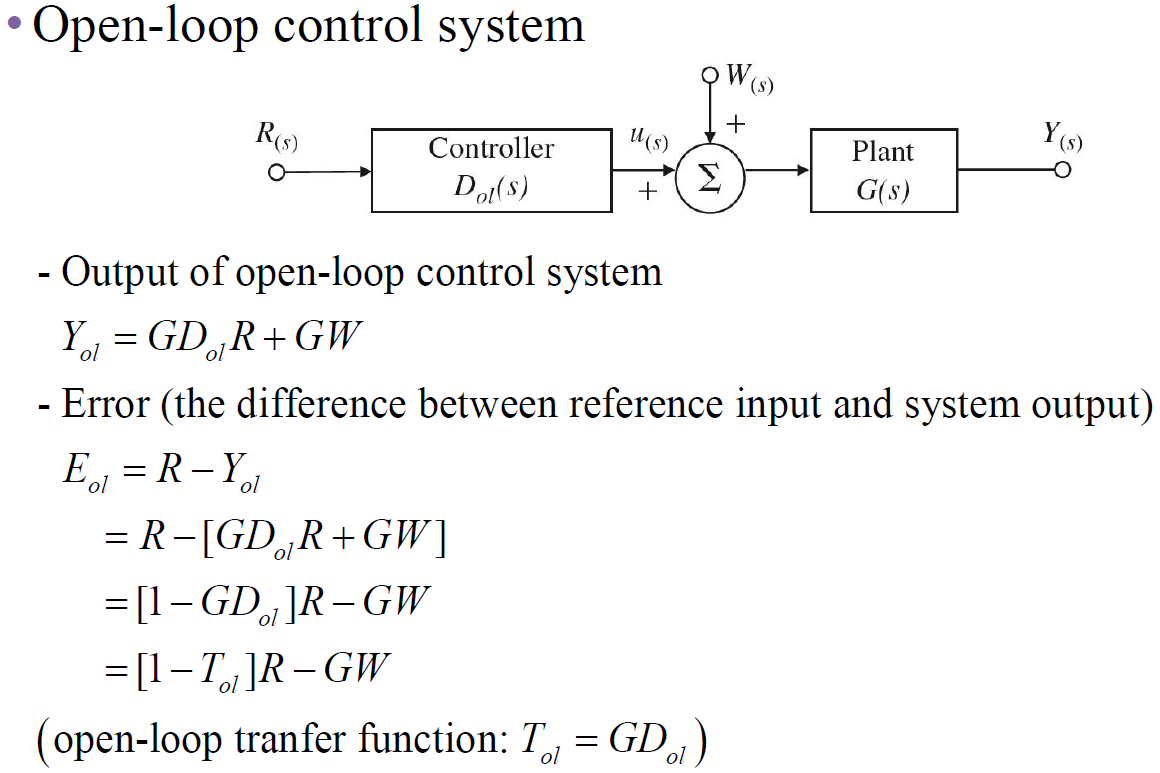
• 시스템이 stable하려면 $G(s),D(s)$가 다 stable 해야 한다.

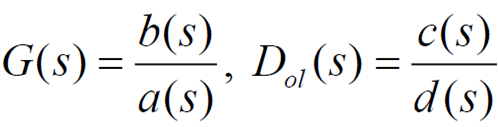
$\Rightarrow a(s),d(s)$의 근 : 음수

• open-loop는 unstable한 plant를 controller를 통해 stable한 전달함수로 변환 불가능
  • controller $D(s)$가 $G(s)W(s)$에 대응 불가

2-2. Feedback loop system

• $R(s)$ : 출력이 따라가야 하는 레퍼런스 입력
• $W(s)$ : 외란
• $V(s)$ : 센서 노이즈

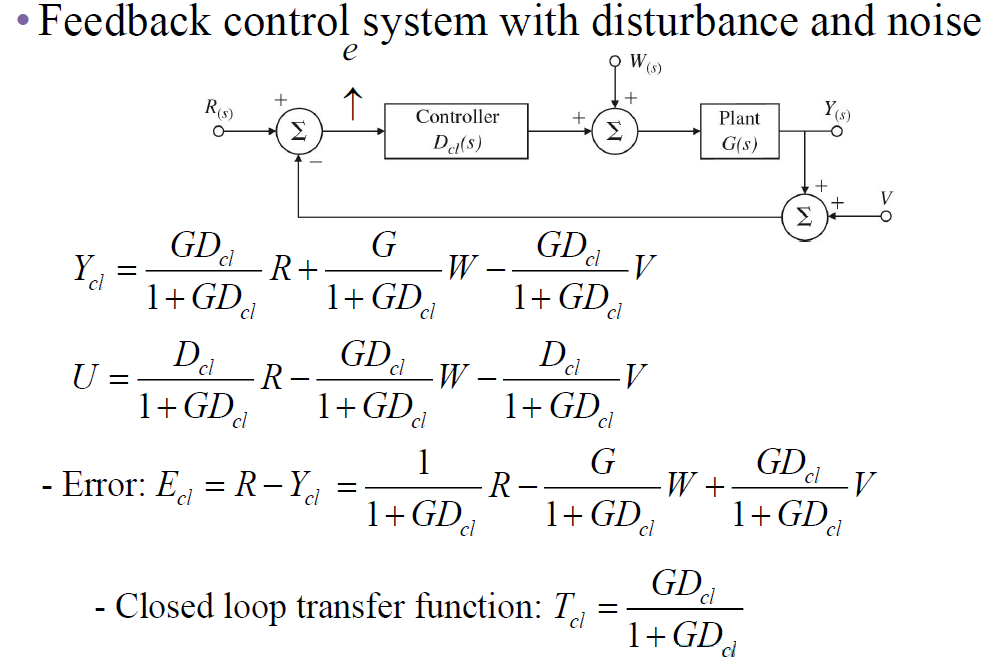
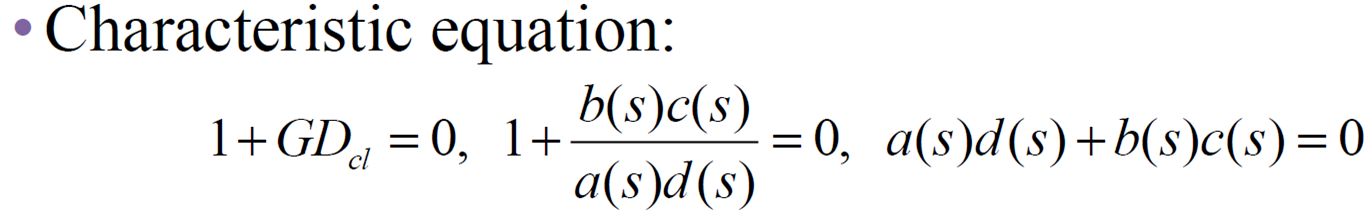
$\Rightarrow$ unstable한 plant를 controller를 통해 stable한 전달함수로 변환 가능

ex)

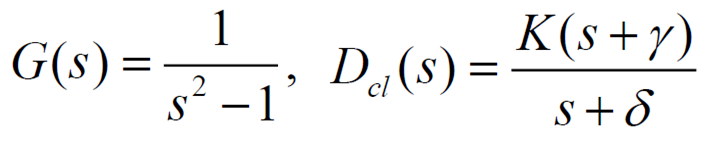
• $G(s)$ : unstable plant

$\Rightarrow 1+G(s)D_{cl}(s)=0\rightarrow (s+1)(s-1)(s+\sigma)+K(s+\gamma)=0$
$(\gamma=1)\Rightarrow(s+1)(s^2+(\delta-1)s-\delta+K)=(s+1)(s^2+2\xi\omega_{n}s+\omega_{n}^2)=0$


$\Rightarrow$ 이렇게 unstable한 plant를 controller를 통해 stable한 전달함수로 변환 가능

두 경우 모두 unstable pole을 pole-zero cancellation으로 지우는 방법은 지양
(시스템을 정확히 파악할 수 없는데 시스템을 건드리는 행위)

3. Regulation

• 출력이 레퍼런스 입력을 잘 따라가는 것을 희망 => Error = 0에 가깝도록

3-1. open-loop

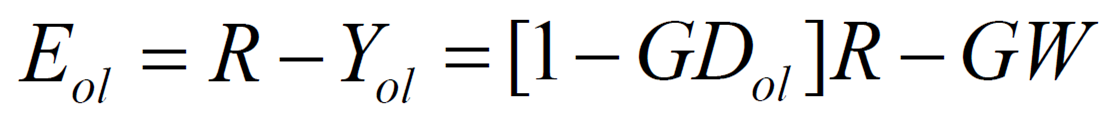
$\Rightarrow$ Error는 작아져도 외란을 제어 불가

3-2. closed-loop

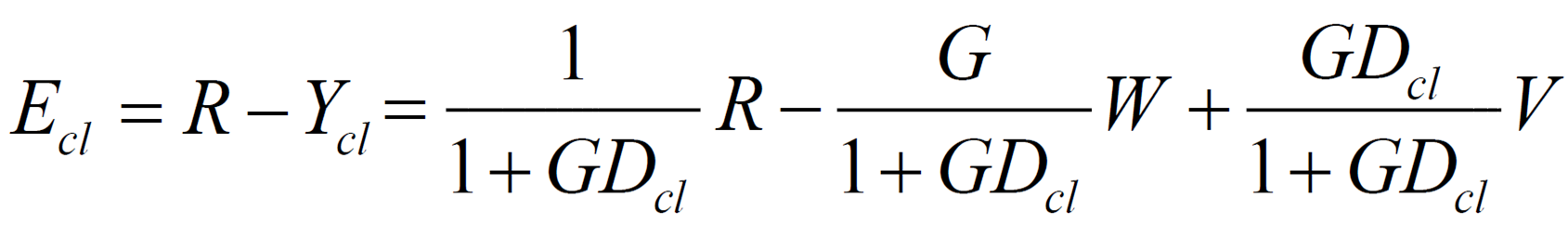
$\Rightarrow 1+GD_{cl}$이 크면 Error $\darr$ $\Rightarrow$ $D_{cl}(s)$ 조절하여 $1+GD_{cl}$ 크기 조절 가능 + 외란 크기 조절 가능
$But, D_{cl}(s)$가 너무 크면 $V$(노이즈)가 그대로 반영

• $W$(외란)은 보통 저주파, $V$(노이즈)는 보통 고주파 $\rightarrow$ 주파수영역에 따라 $D_cl(j\omega)$ 값 조절하여 외란 or 노이즈 감소, $R$(reference input)또한 보통 저주파

4. Sensitivity

• $G$(plant)에 변화가 있을 때 전체 시스템의 전달함수에 발생하는 변화
  $G\rightarrow G+\delta G \Rightarrow T\rightarrow T+\delta T,$
  $\Rightarrow$ Sensitivity : $S_{G}^T=\frac{\frac{\delta T}{T}}{\frac{\delta G}{G}}$

4-1. open-loop

• controller 변화 x
  

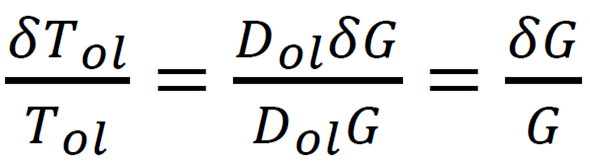
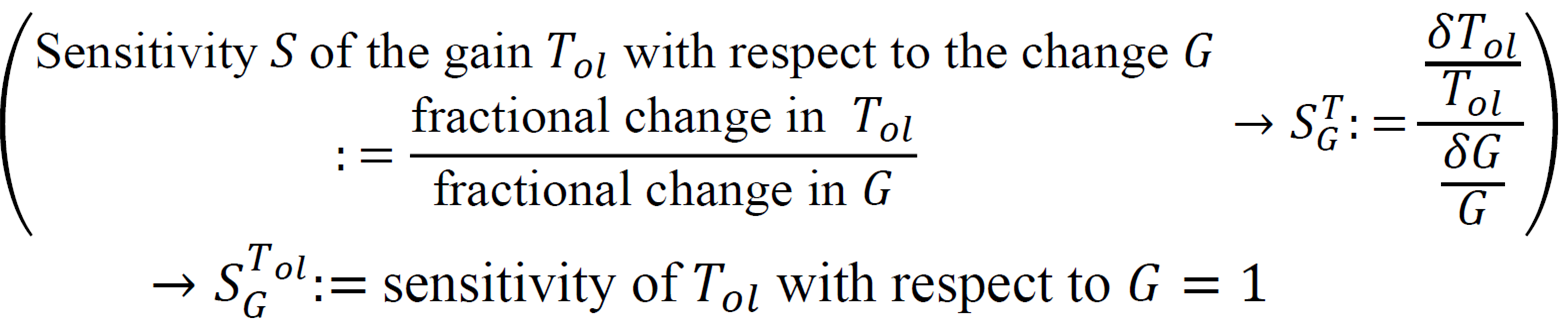
4-2. closed-loop

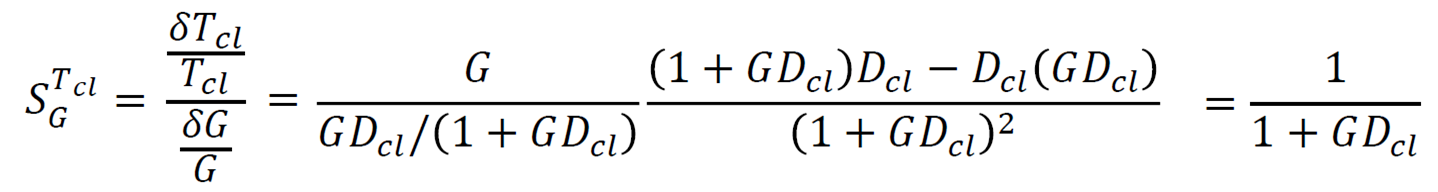
$\Rightarrow D_{d}$(controller)로 stability 조정 가능

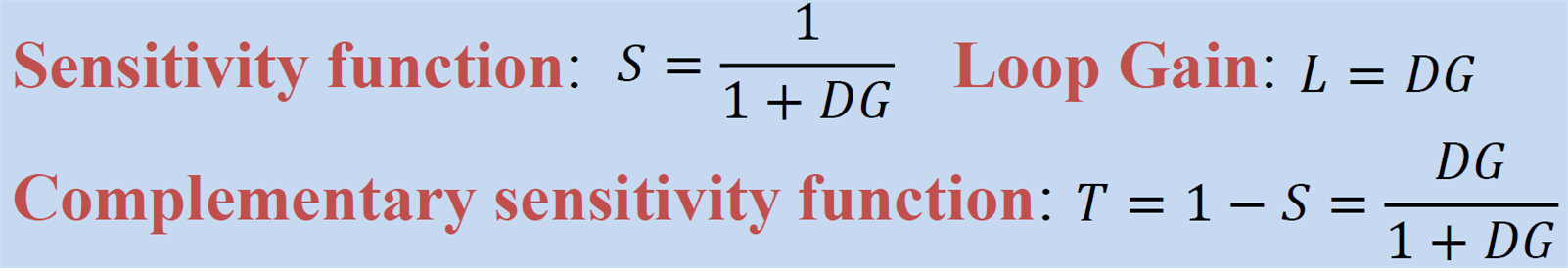
$\Rightarrow E_{cl}=(S)R-(SG)W+(T)V$ $\Rightarrow T$와 $S$를 둘다 줄이는 건 불가능

• 앞서 말했듯이 $R,W$(외란)은 보통 저주파, $V$(노이즈)는 고주파
  $\Rightarrow$ 저주파 영역 $\rightarrow(S\rightarrow0),$ 고주파 영역 $\rightarrow(T\rightarrow0)$