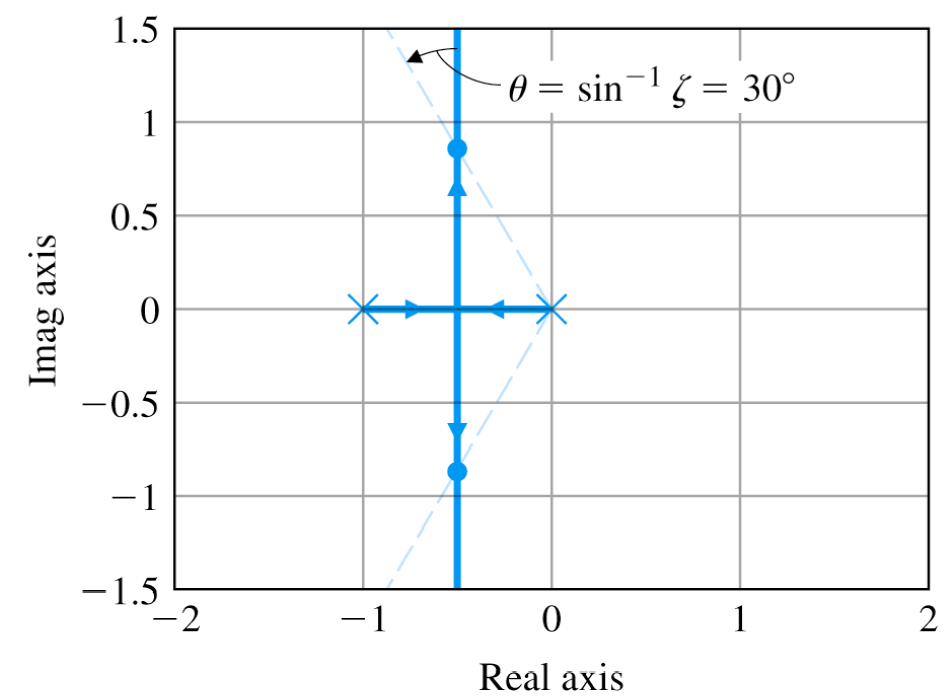
1. Root-Locus

• closed-loop 시스템의 파라미터의 변화에 따른 pole의 궤적

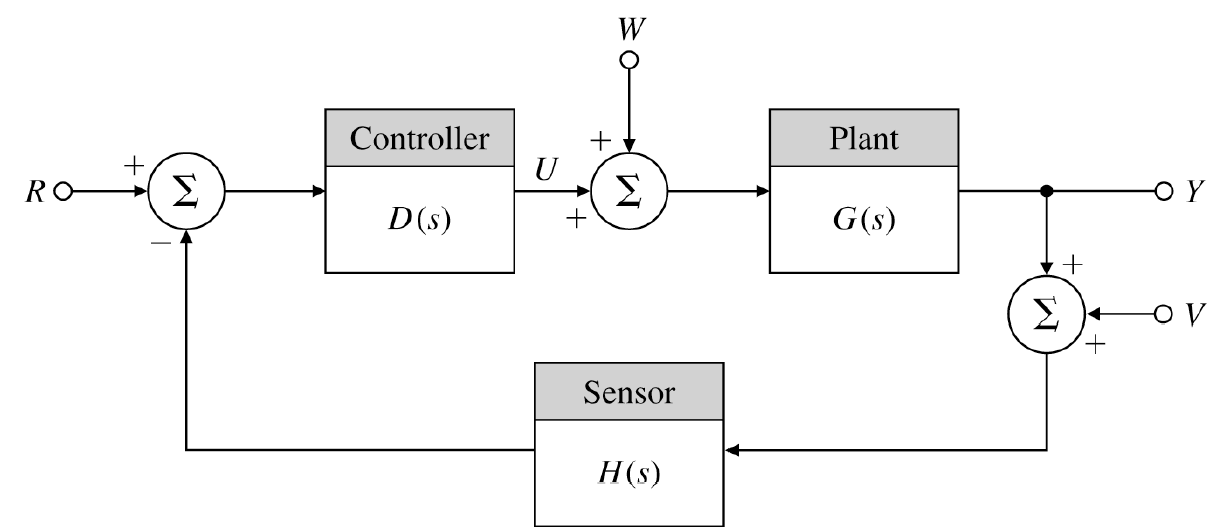
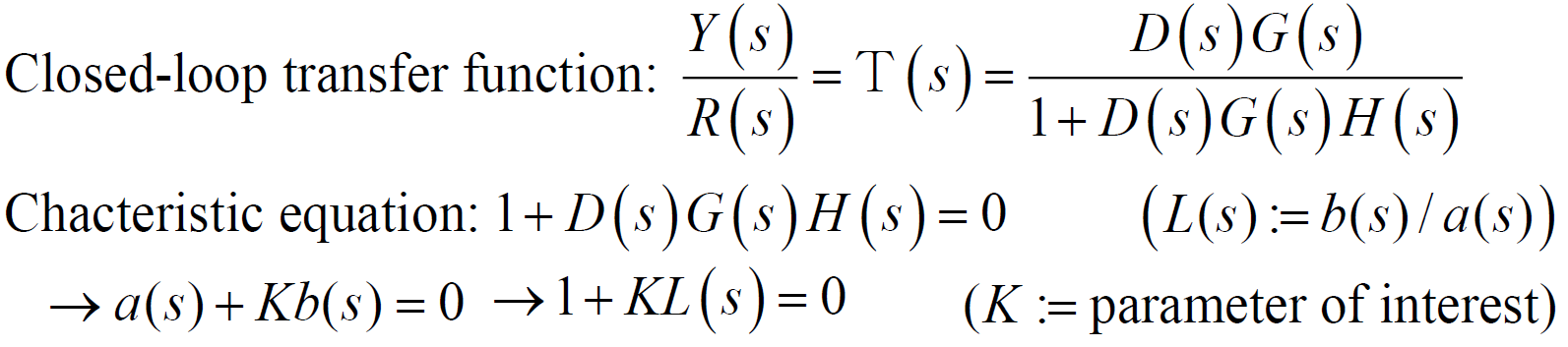
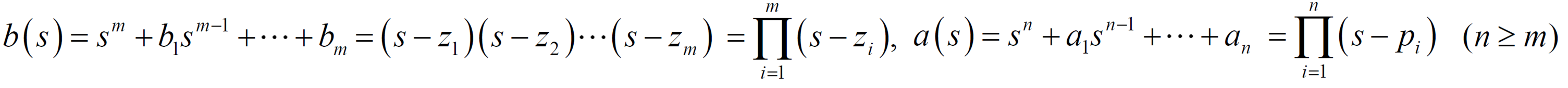
$\Rightarrow K$의 변화(0 ~ $\infin$ or $-\infin$ ~ 0)에 따른 pole의 궤적을 구해볼 것이다.

• 보통 $L(s)$는 open-loop 에서의 전달함수

ex) Motor Position Control Root Locus

• $c=1, A$를 미지수로 둠

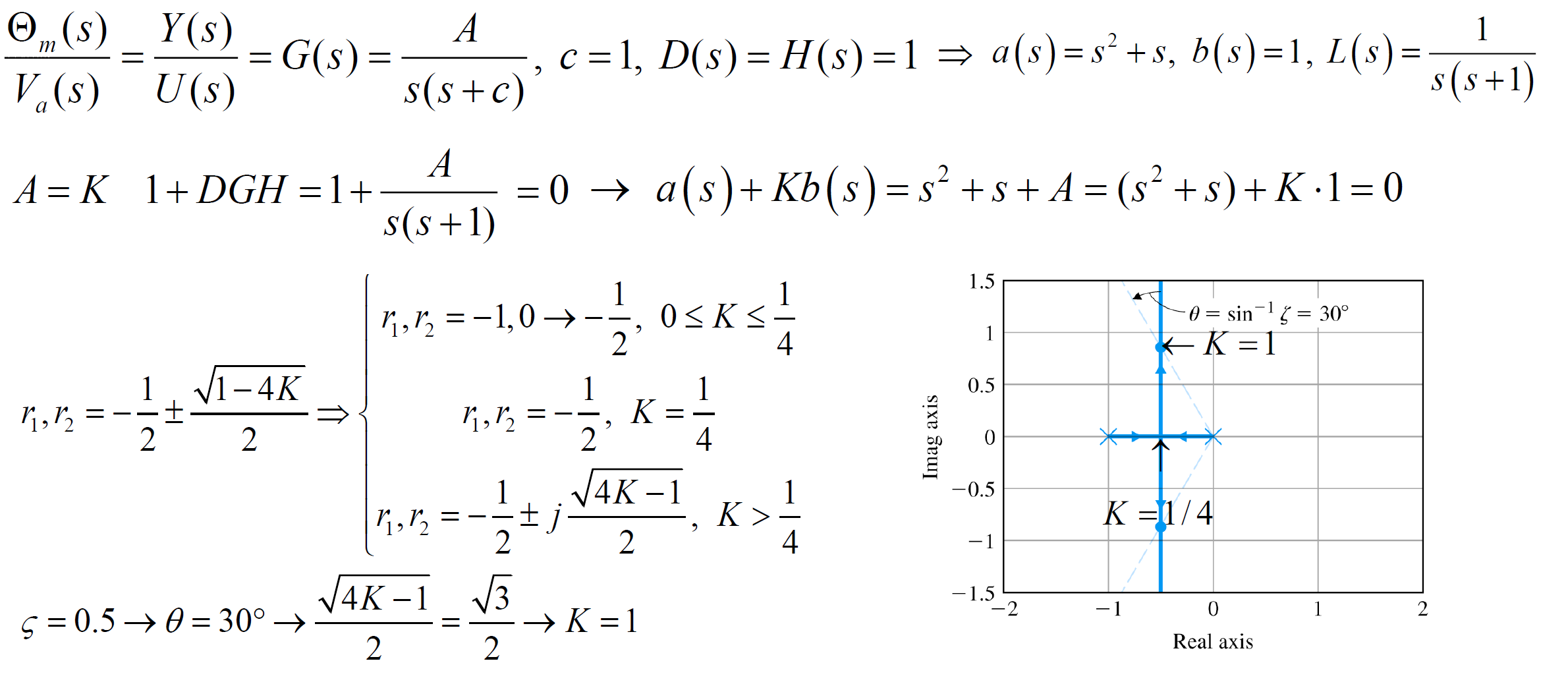
• n=2일 때 근 2개, branch(가지) 2개
• 시작은 $K=0$, 즉 $L(s)$의 pole에서 시작
• Breakaway points : pole이 실수부에서 허수부로 바뀌는 지점

Root Locus 궤적 상에 점이 있는지 확인하는 가이드라인

• $l$ : 1 ~ n-m 까지의 정수
  (n : pole의 개수, m : 유한대 범위의 zero의 개수 => n-m : 무한대 상의 zero 개수)
• $L(s)=-\frac{1}{K}\quad\Rightarrow\vert L(s)\vert =\frac{1}{K},\quad\angle L(s)=180^\circ$ (양의 x축이 0도 기준)
  $\Rightarrow \angle L(s)=180^\circ$ 가 되는지 확인하는 방법을 알아보겠다.

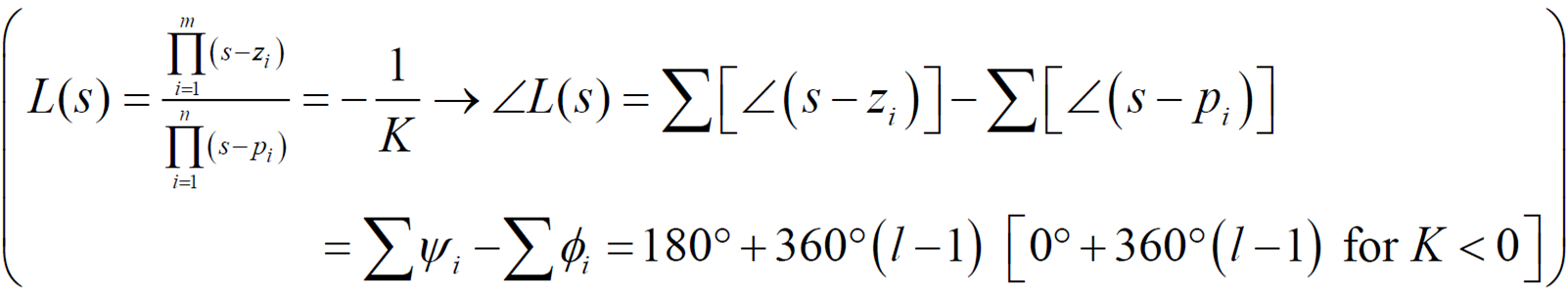
ex) $L(s)=\frac{s+1}{s(s+5)[(s+2)^2+4]}, \quad (1+L(s)=0)$

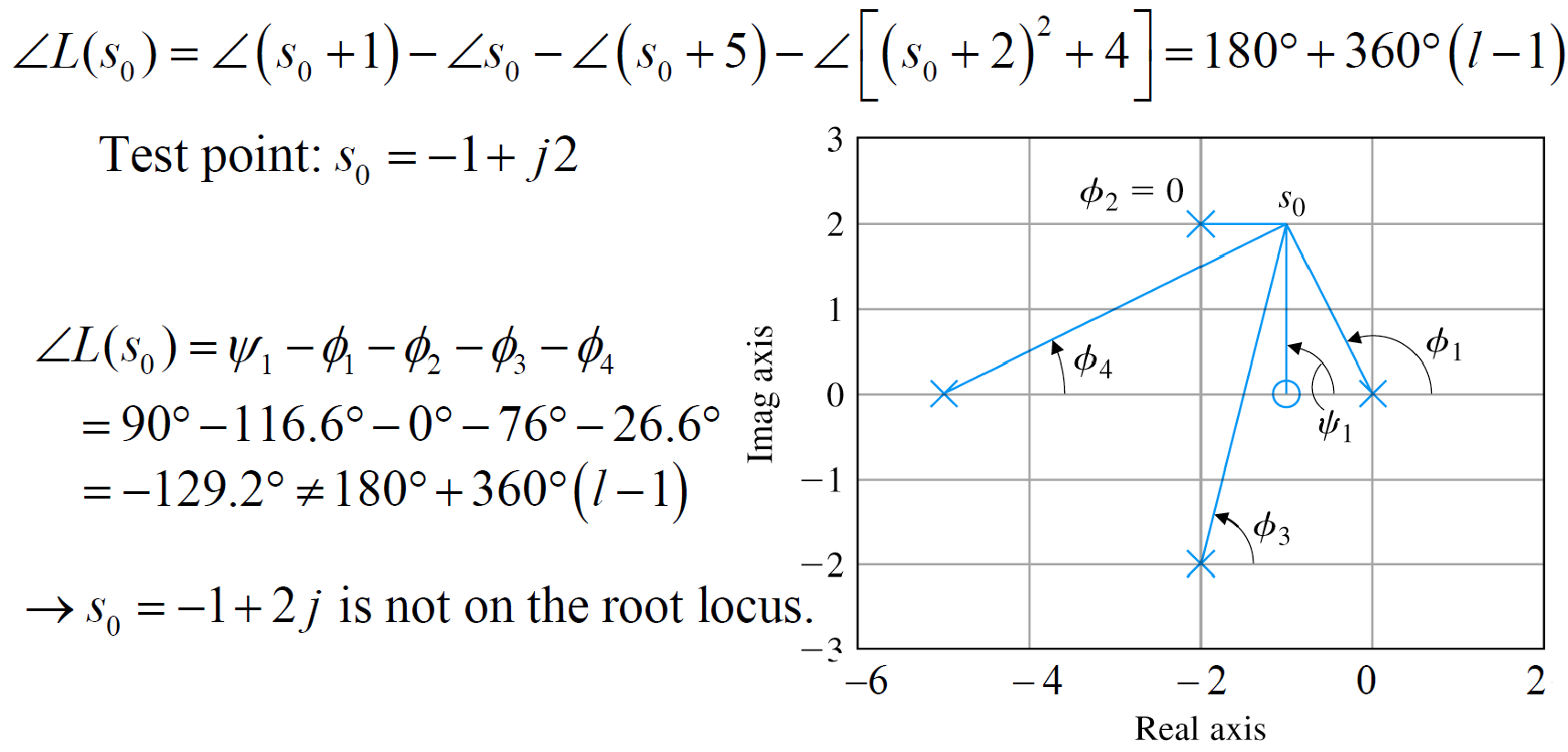
$\Rightarrow$ 이렇게 선택한 point가 Root Locus 궤적 상의 점인지 알 수 있다.

이제 Root Locus를 그리는 방법 소개

2. Rules for Sketching a Root Locus

• Root Locus를 그리는 5가지 규칙

2-1. Rule 1

• n개의 branch가 $L(s)$의 pole에서 시작해서 m개의 branch는 $L(s)$의 zero에서 끝남 $\Rightarrow$ n-m개의 branch는 무한대로 뻗어나감

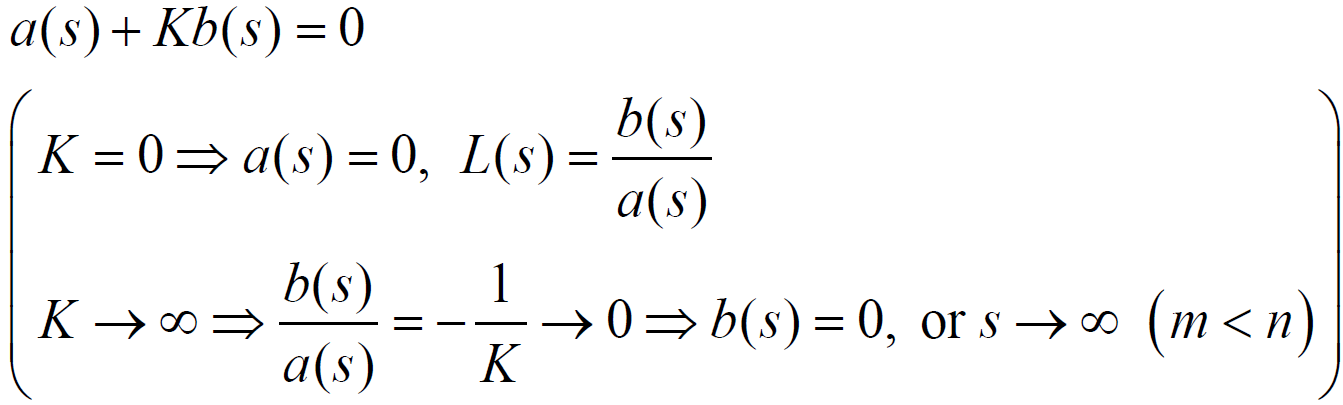
• 시작 : $K=0 : a(s)=0$이 돼서 $L(s)$의 pole에서 시작 (n개 branch)
• 끝 : $K=\infin : b(s)=0$이 돼서 $L(s)$의 zero에서 끝 (m개 branch)
  or $s=\infin$이 되면 $L(s)=0$ 만족 (n-m개 branch)
  

2-2. Rule 2

• 홀수 개의 pole과 zero가 실수축에 존재
• test point의 오른쪽 존재하는 pole & zero가 홀수 개면 그 test point는 Root Locus 상에 존재

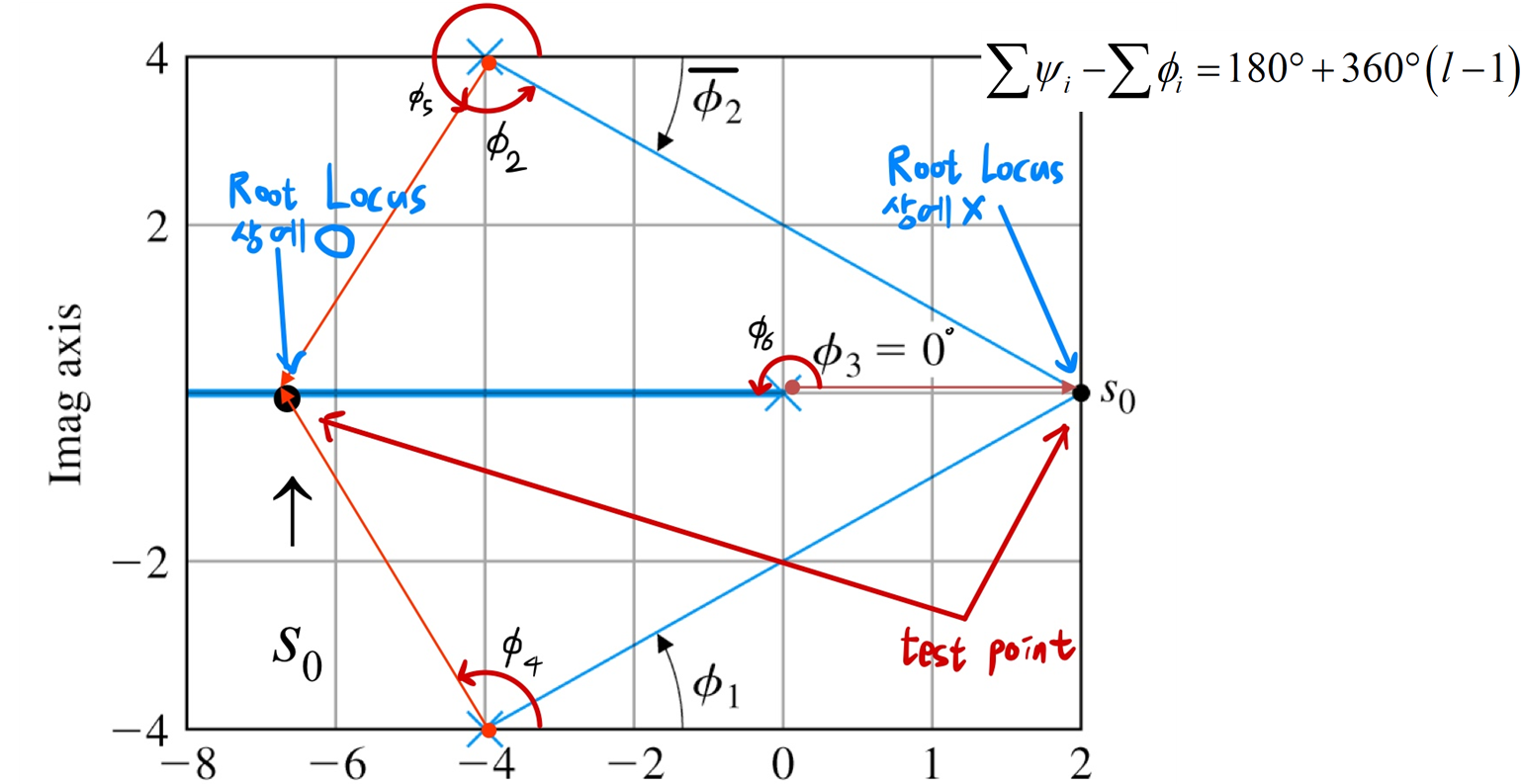
2-3. Rule 3

• $K$가 매우 커지면(s 크기도 증가) m개의 branch는 유한대 범위의 zero로 끝나고 n-m개의 branch는 무한대에 존재하는 zero로 발산. 거기서 n-m개의 branch가 $\alpha$점에서 $\phi_l$의 각도로 뻗어나가는 직선을 점근선으로써 뻗어나감

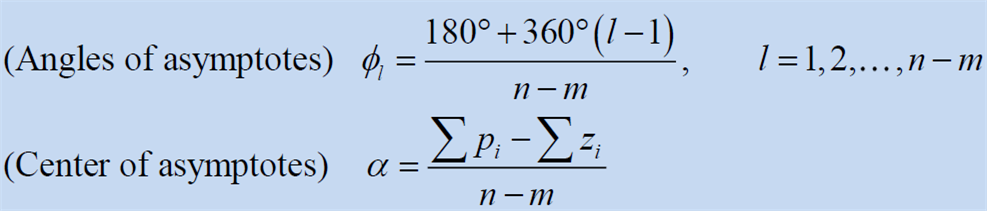
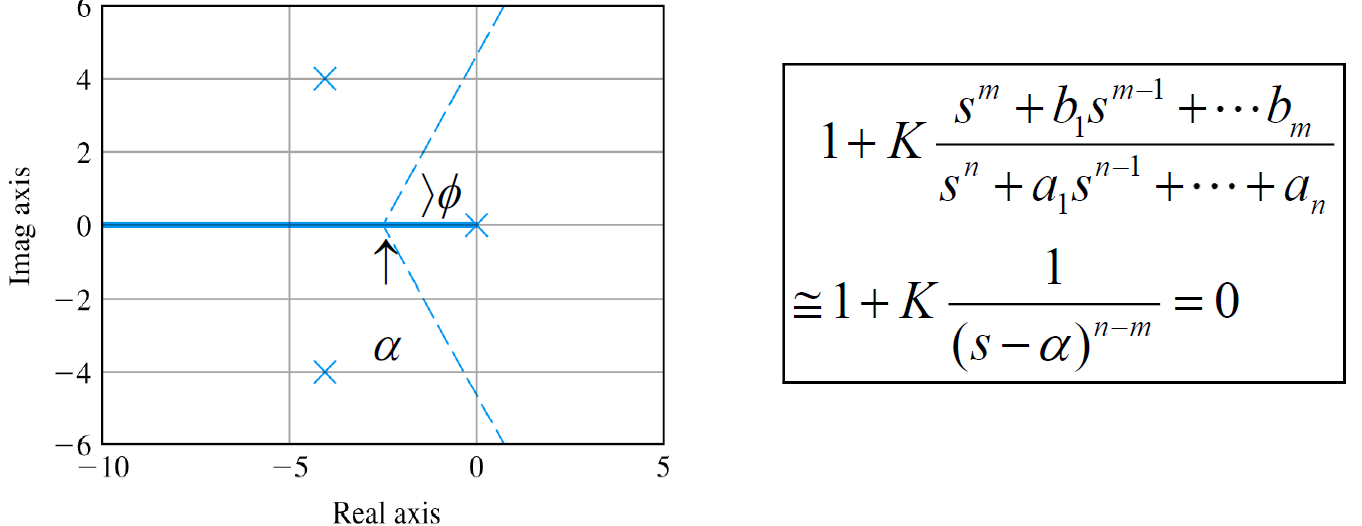
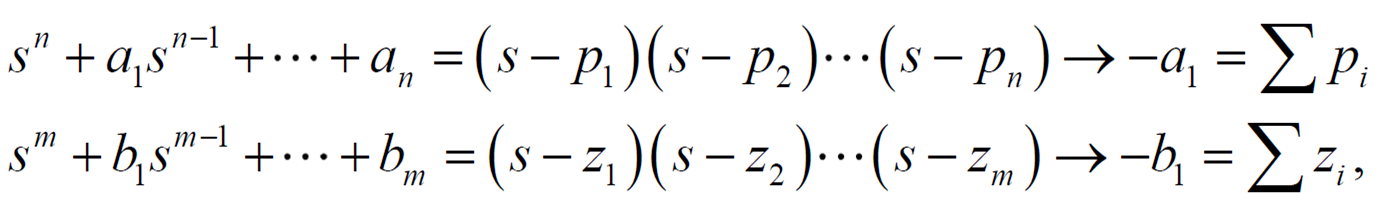
정리하면

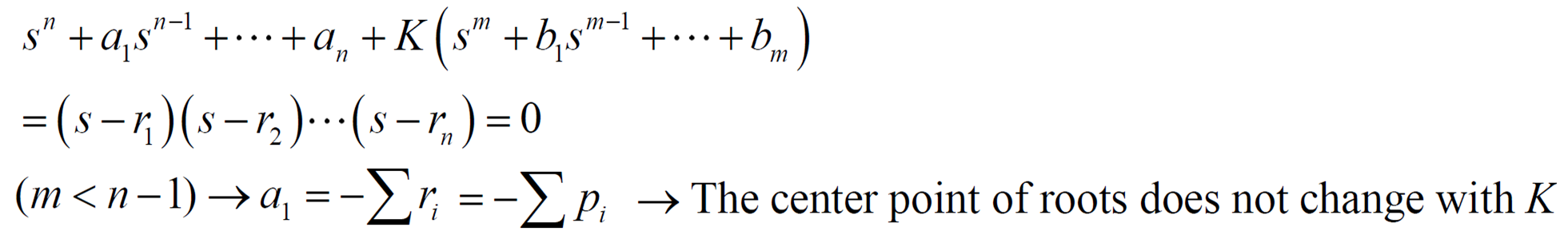
$\Rightarrow$ Root locus의 근의 합이 의 $L(s)$의 pole의 합과 같다.
1. m개의 근이 zero로 향하니 근의 m개의 합은 zero의 합 $\sum{i=1}^{m} z_i$
2. 나머지 n-m개의 근의 종점은 $s\rightarrow 0$일 때 이므로 근의 n-m개의 합은 다음과 같다.

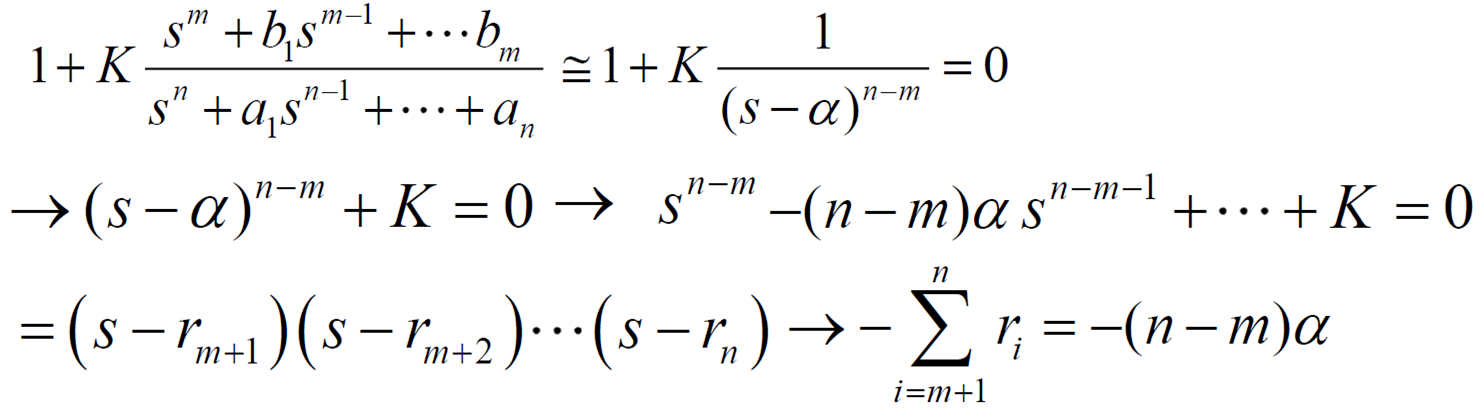
그래서 n-1 > m인 경우에 $\alpha$는 다음과 같이 된다.

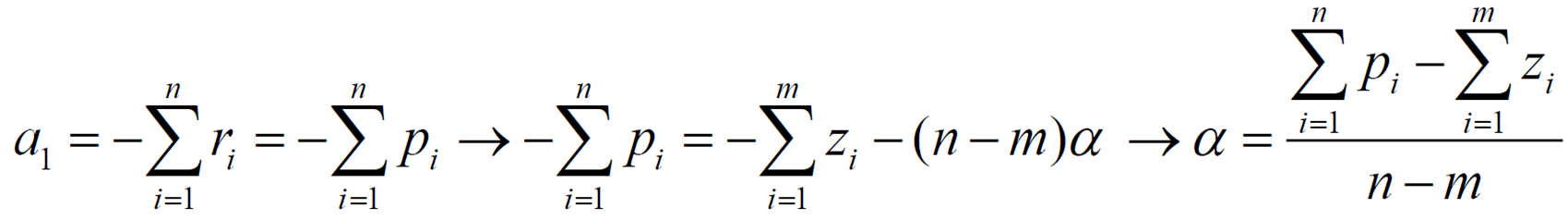
인 경우에는 당연히 음의 실수축의 무한대로 뻗어나가는 근 말고는 다 유한대 범위의 zero에 수렴하므로 점근선을 생각할 필요 없다.

2-4. Rule 4

• Root Locus가 어떤 궤적을 그리며 움직일지
• 근이 pole에서 어떻게 궤적을 시작할지
• zero로 수렴하는 근이 어떤 각도로 수렴할지
• q : 같은 위치에 중복된 근 개수

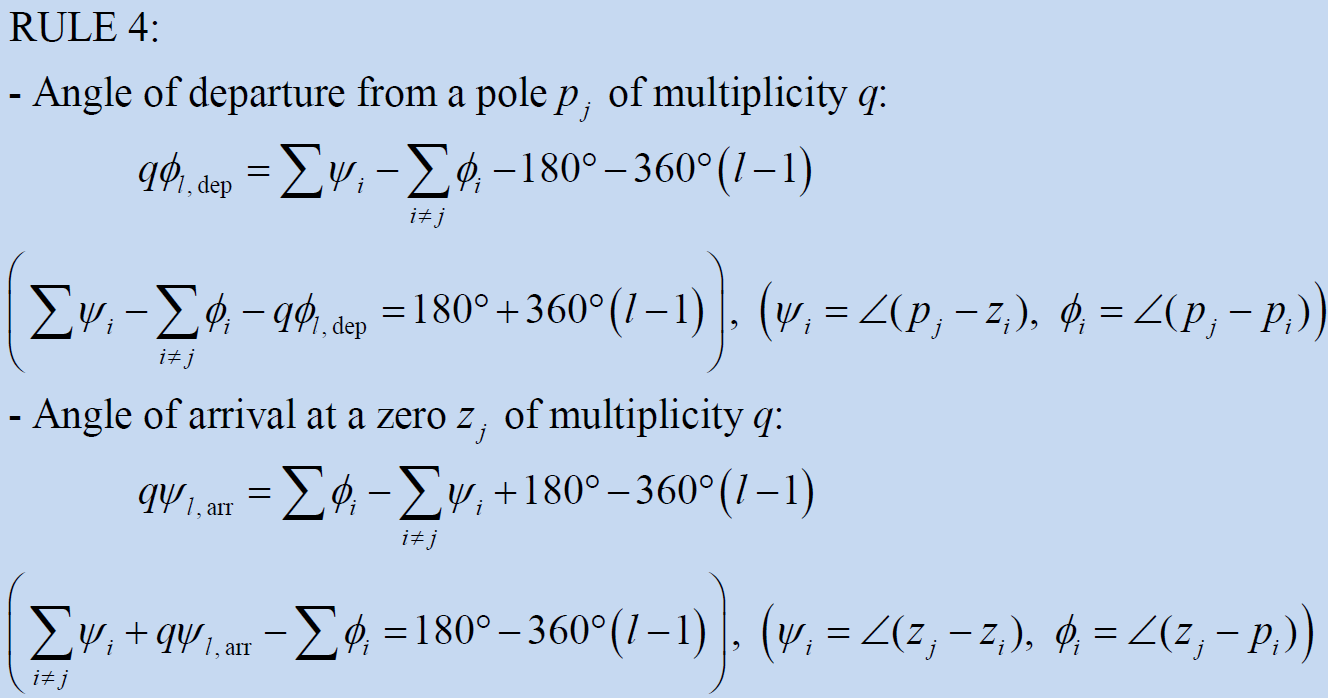
ex) pole 2가 어떤 궤적으로 움직일지 (zero x)

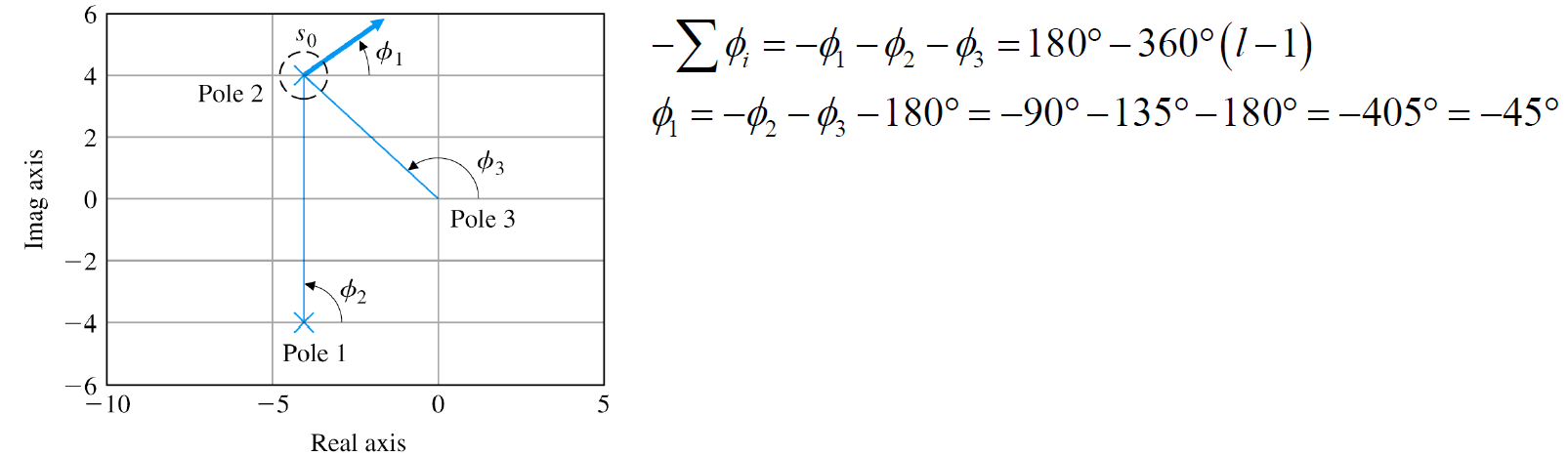
$\Rightarrow$ Pole 2는 $\phi_1$각도 방향으로 움직이기 시작할 것

ex) $K$가 어느 범위에 있어야 시스템 stable 할지 (Routh criterion)

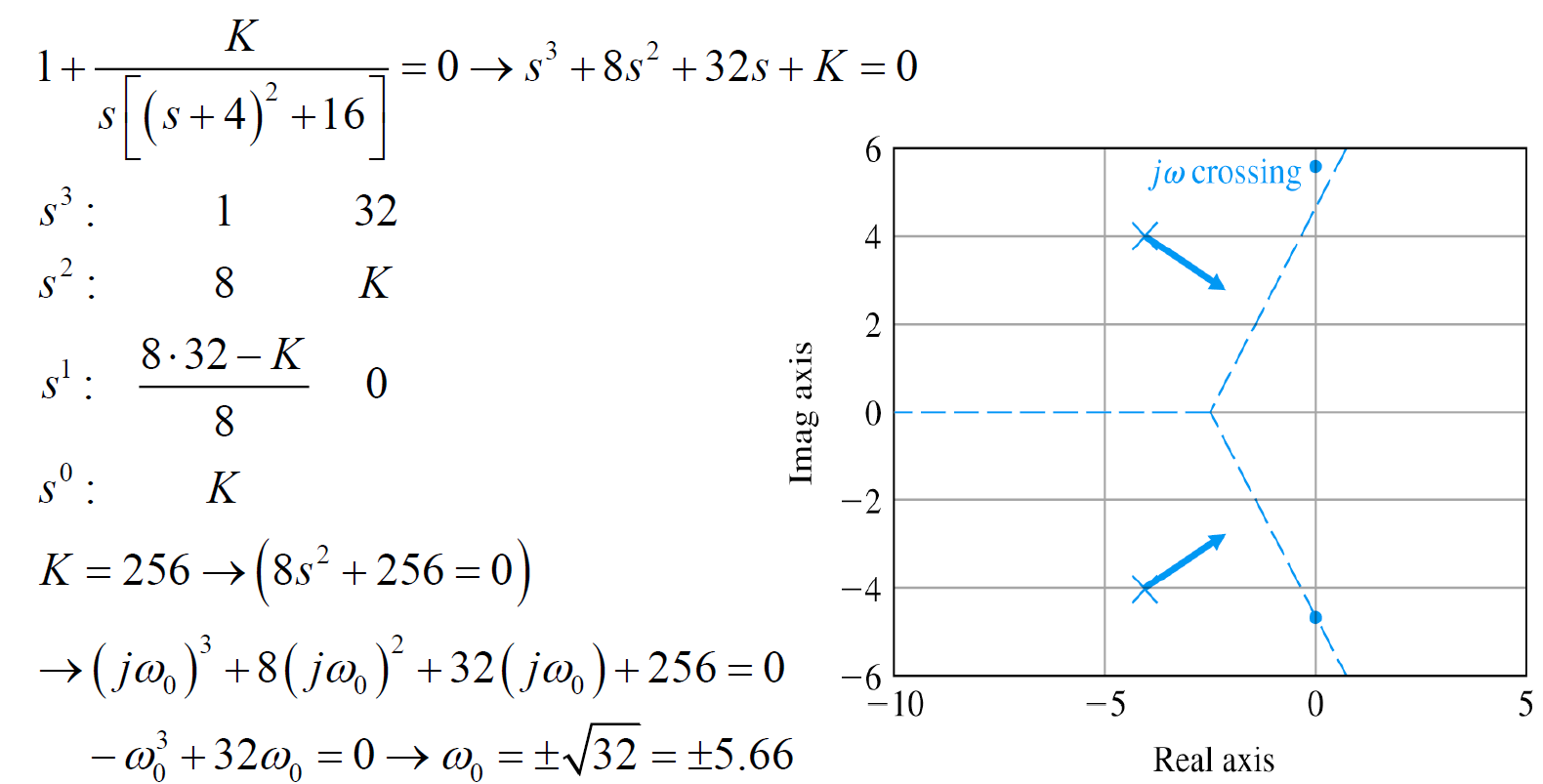
$\Rightarrow K=256$일 때 안정한 상태의 경계

2-5. Rule 5

• Root Locus가 궤적을 그리다가 근이 만나는 점 (중근)이 생기는 경우에 그 위치의 필요조건(후보) $\Rightarrow$ 주의) 후보 이므로 무조건 그 위치가 중근인 것은 아님

그 위치는 \frac{dL(s)}{ds}=\frac{b^'(s)a(s)-b(s)a^'(s)}{a^2(s)}=0 만족 $\Rightarrow b\frac{da}{ds}-a\frac{db}{ds}=0$ 만족

• 중근에 근이 접근하는 각도 : $\frac{180^\circ+260^\circ(l-1)}{q}$

증명

• 궤적 상의 근과 그 근에 해당하는 $K$를 특성 방정식에 대입하면 당연히 0이 될 것

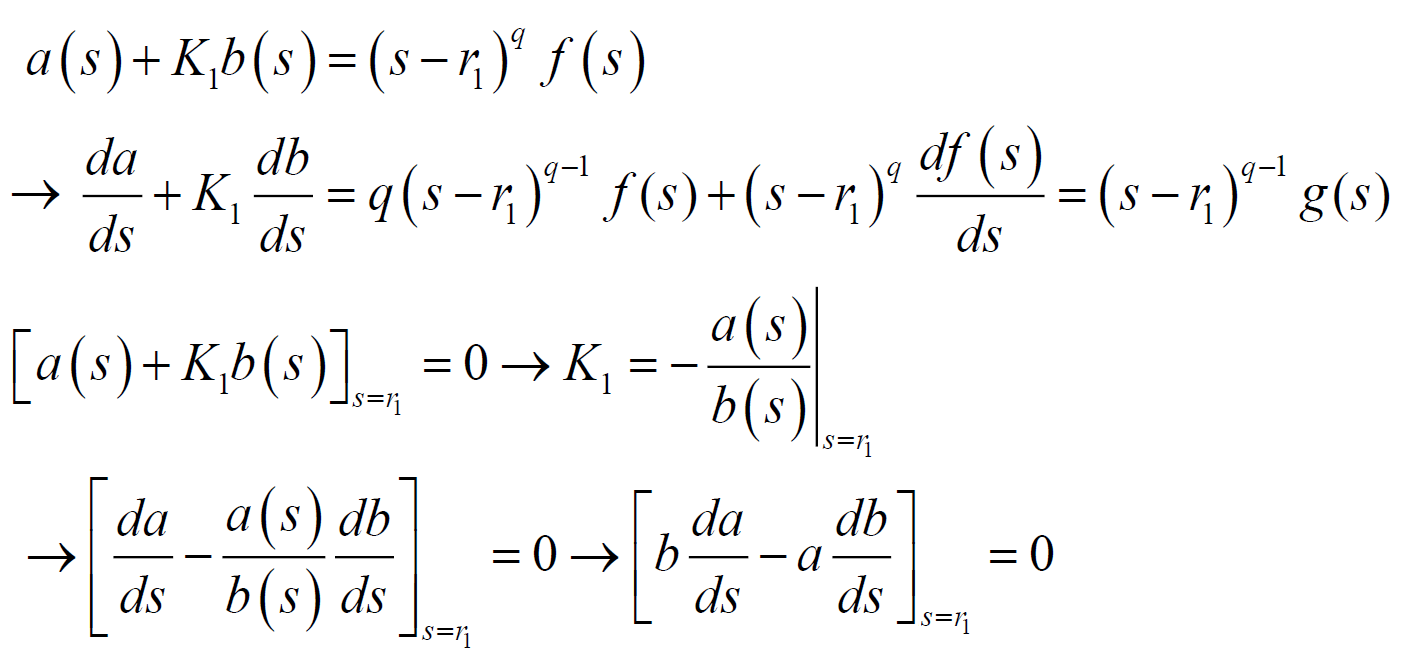
ex) 이 필요조건으로 나온 근이 무조건 중근은 아닌 이유

$\Rightarrow$ 애초에 복소수를 가진 중근이 생기려면 복소수 근은 2개씩 쌍(켤레근)으로 있기 때문에 2 * n 개, 즉 최소 근이 4개는 되어야 함. 하지만 위의 식은 n=3이므로 모순. 그래서 이를 통해 Root Locus가 중근을 가지는지 아닌지 판단 가능

3. 특정 지점 이후의 Root Locus의 궤적

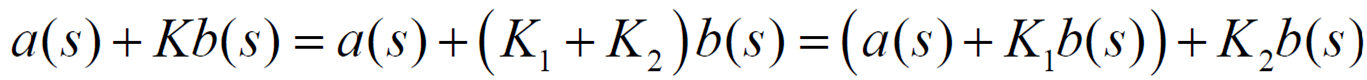
ex) $K\geq\frac{1}{4}$일 때의 Root Locus

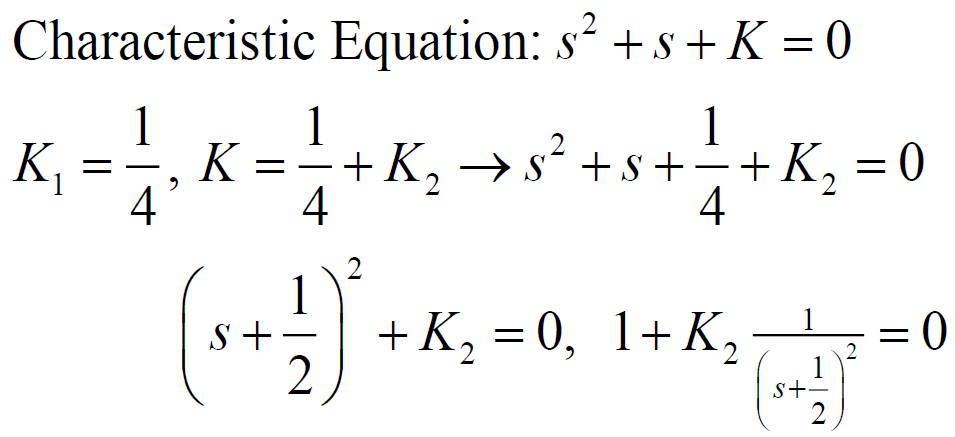
$\Rightarrow s=-\frac{1}{2}$ 에서 중근을 가진 채 Root Locus가 시작되며 궤적은 중근이 $2\phi_1=0^\circ-0^\circ-180^\circ-360^\circ(1-1), 2\phi_2=0^\circ-0^\circ-180^\circ-360^\circ(2-1)$의 각도로 그린다.