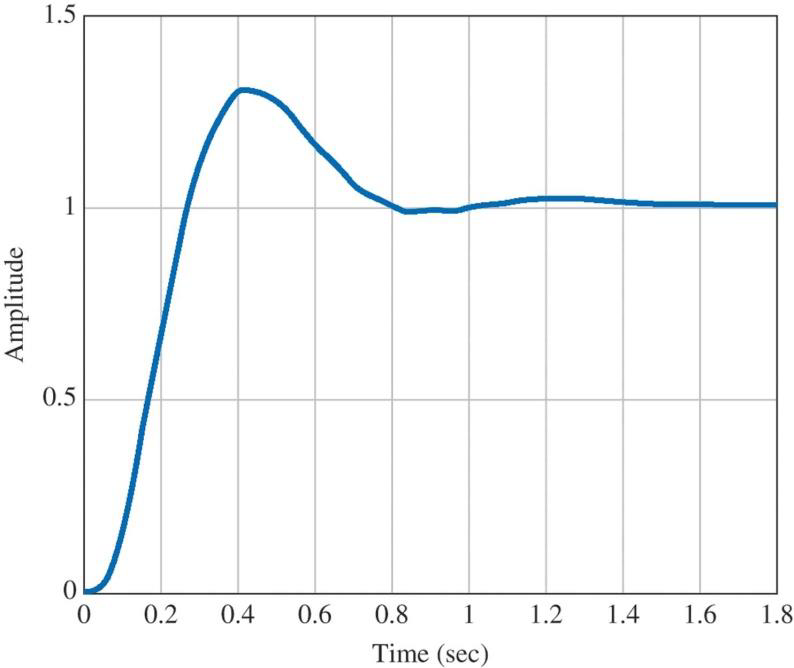
1. 파라미터 수치 정하기
- 원하는 근이 Root Locus의 pole이 되도록
ex) 를 만족하는 근이 어떤 값을 가질지
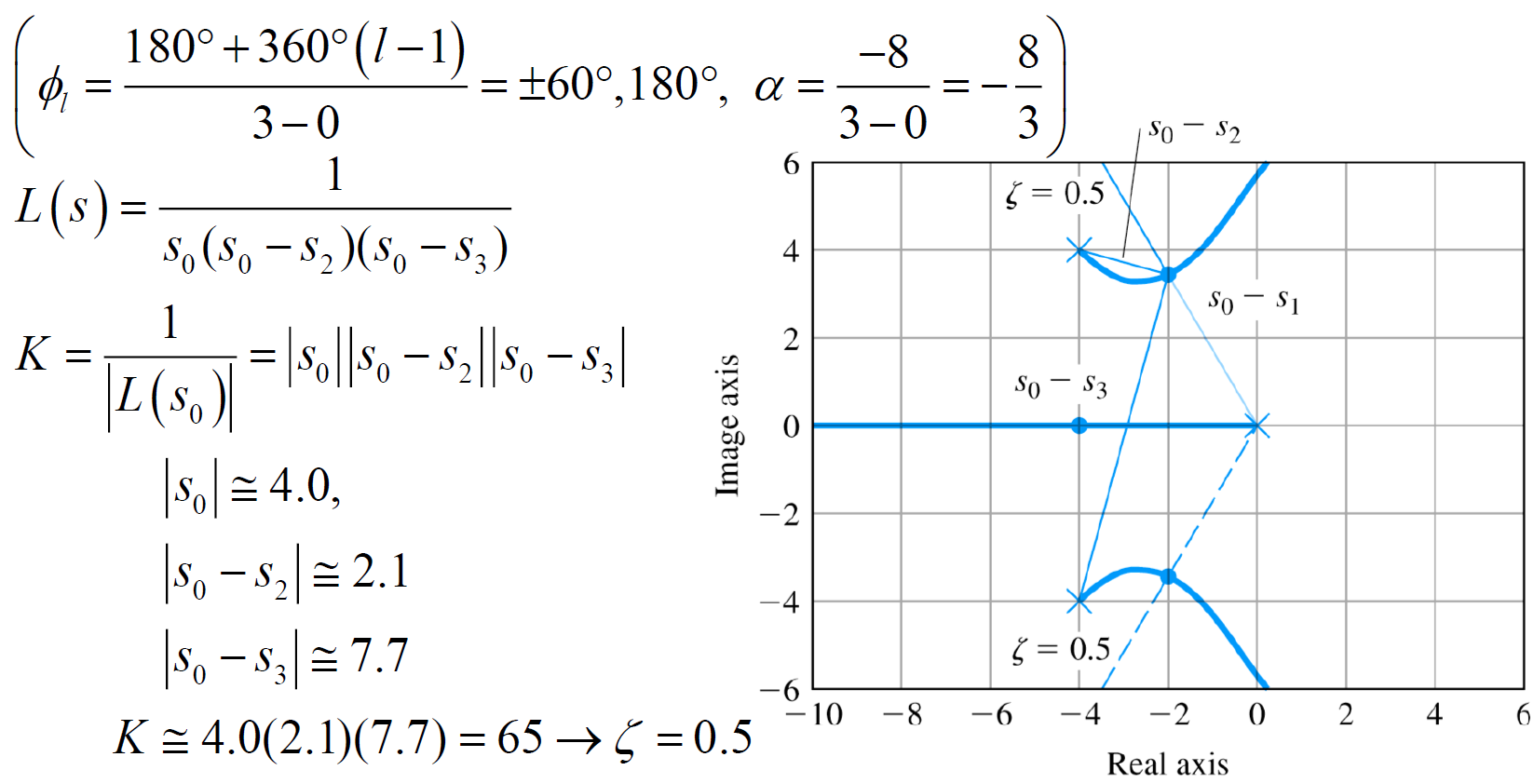
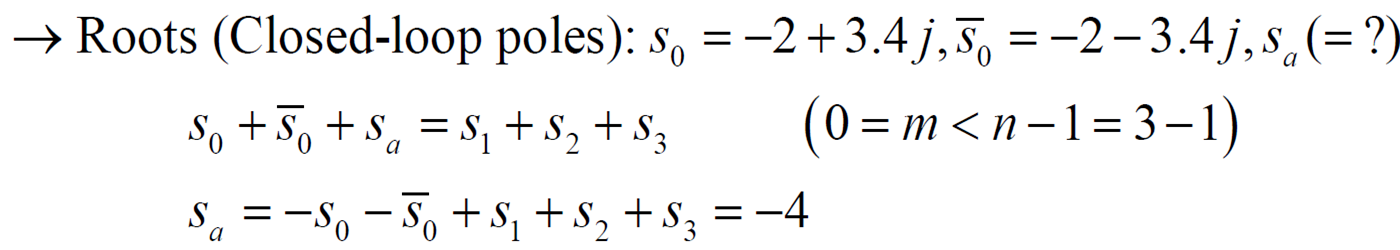
- Dominant poles : 시스템에 영향을 강하게 주는 허수축과 가까운 pole들
허수축에 가까우면 0으로 수렴 느림, 멀면 0으로 수렴 빠름 - Dominant pole과 아닌 pole들을 구분하기 위해 Dominant pole과 아닌 pole들의 거리가 3~5배 차이
- 여태까지 2차 시스템에 관한 시스템 스펙을 알아봤기 때문에 Dominant pole도 2개
ex) 위성 자세 PD제어
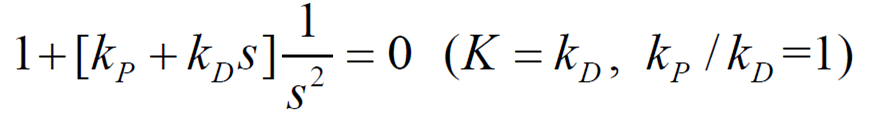
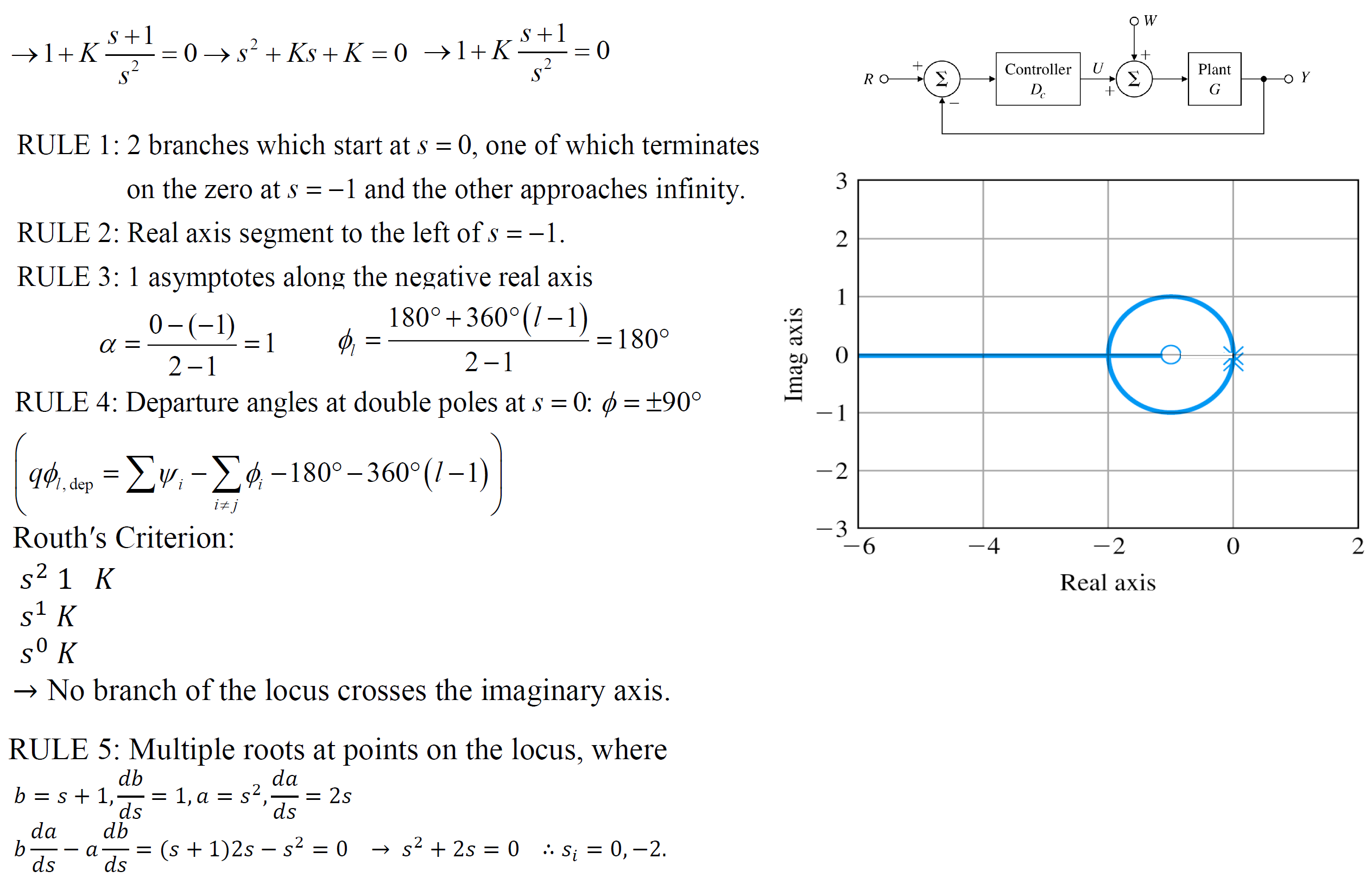
LHP에 있는 zero가 근을 당기는 것을 볼 수 있음 (zero로 근이 수렴해야하기 때문)
하지만 아날로그 회로관점에서 제어기가 미분형태(분자 차수 > 분모 차수)를 가지면 노이즈가 매우 커져 좋지 않다. 그래서 PD제어처럼 미분형태의 제어기를 다음과 같이 만들 것이다.
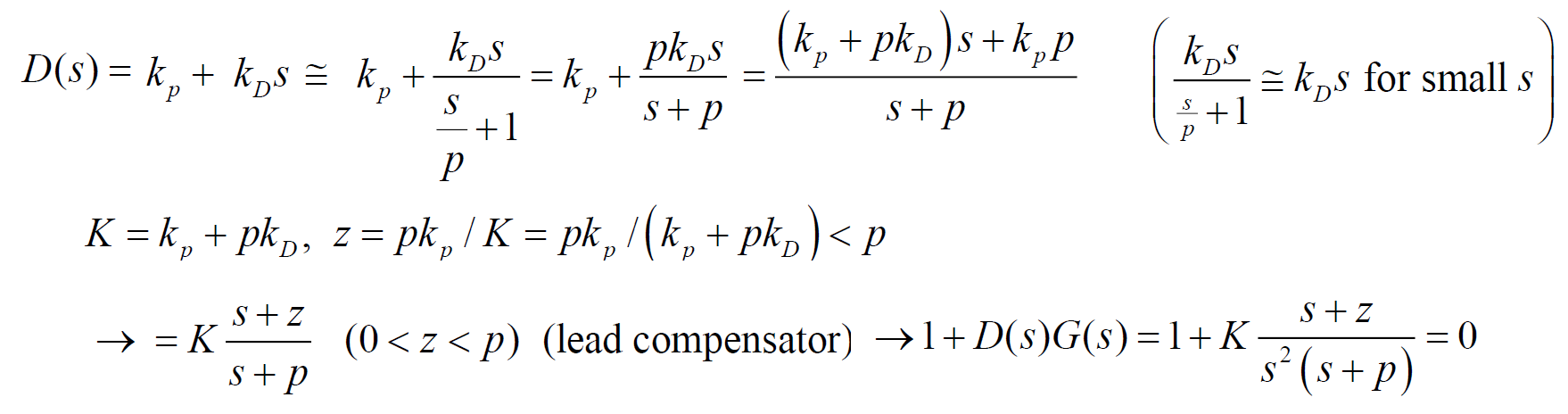
- 큰 (pole)를 추가
이 제어기를 가지고 다시 예제를 풀어볼 것 (zero는 기존처럼 –1, p는 –12로 충분히 큰 값)

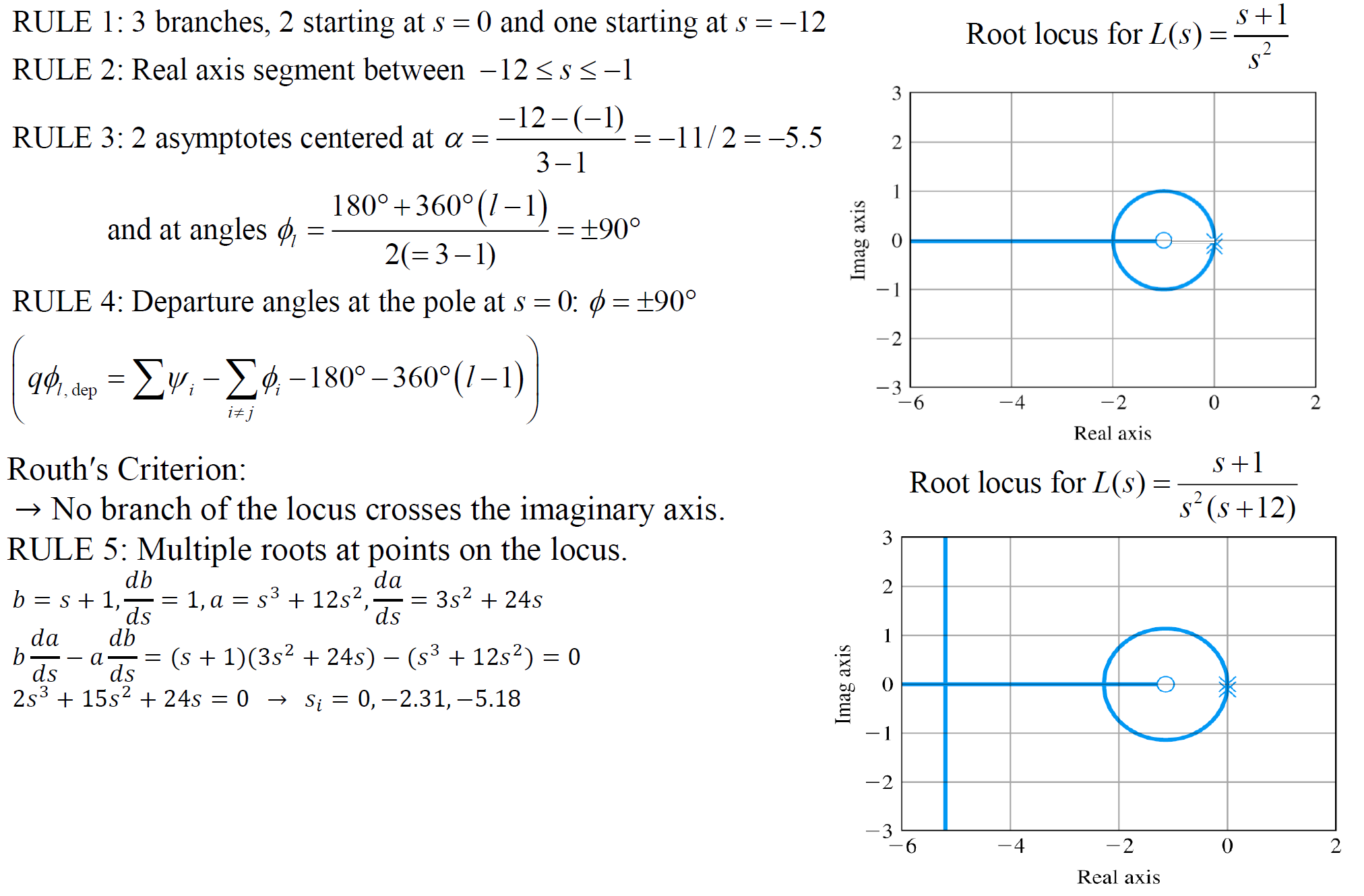
를 충분히 크게 하면 노이즈 문제없이 PD제어와 비슷하게 Root Locus가 그려짐
반대로 작으면 다음과 같이 된다.
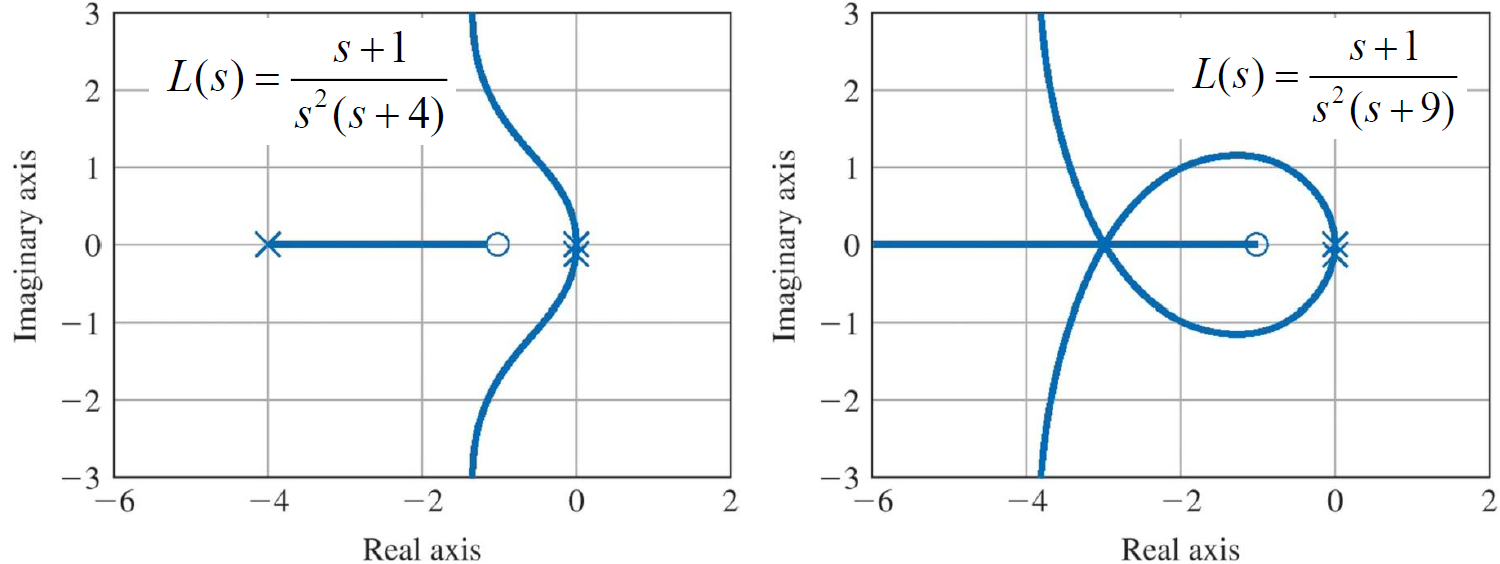
2. 보상기 설계
- 코끼리가 치타처럼 빠르게 달릴 수 없듯이 모델의 스펙을 먼저 파악하고 제어해야한다.
- 제어기의 3종류
- Lead compensator
- Lag compensator
- Notch compensator
2-1. Lead compensator(중점)
- PD제어기와 유사,
- 과도응답 향상, rise time 낮춤, 감쇠비 상승
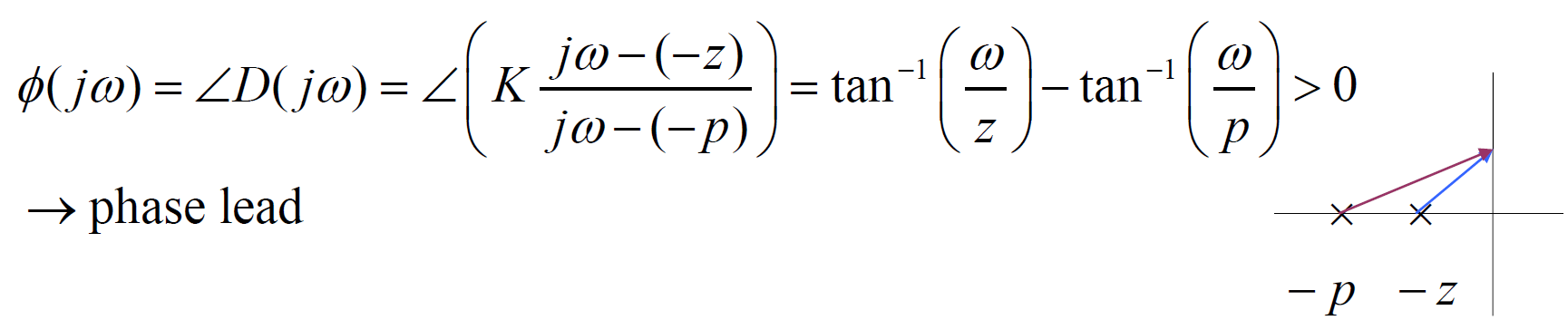
2-2. Lag compensator
- PI제어기와 유사,
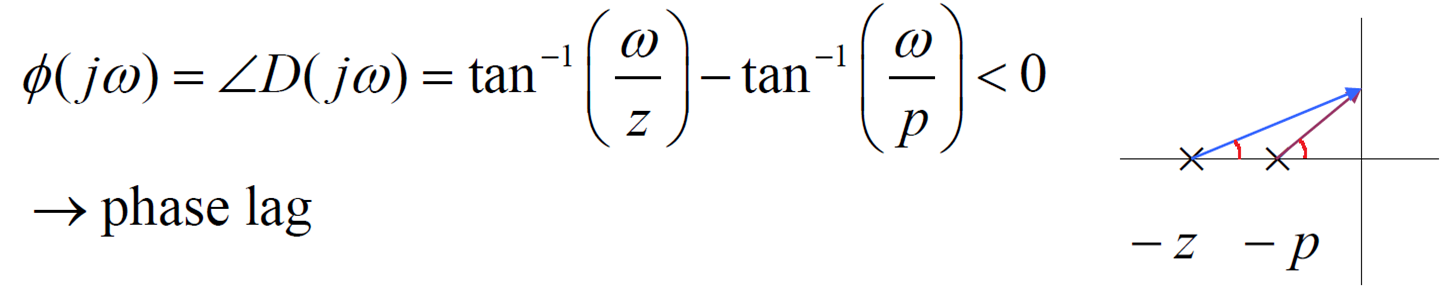
ex) Lead Compensation
- 실선 : P 제어
- 점선 : PD 제어
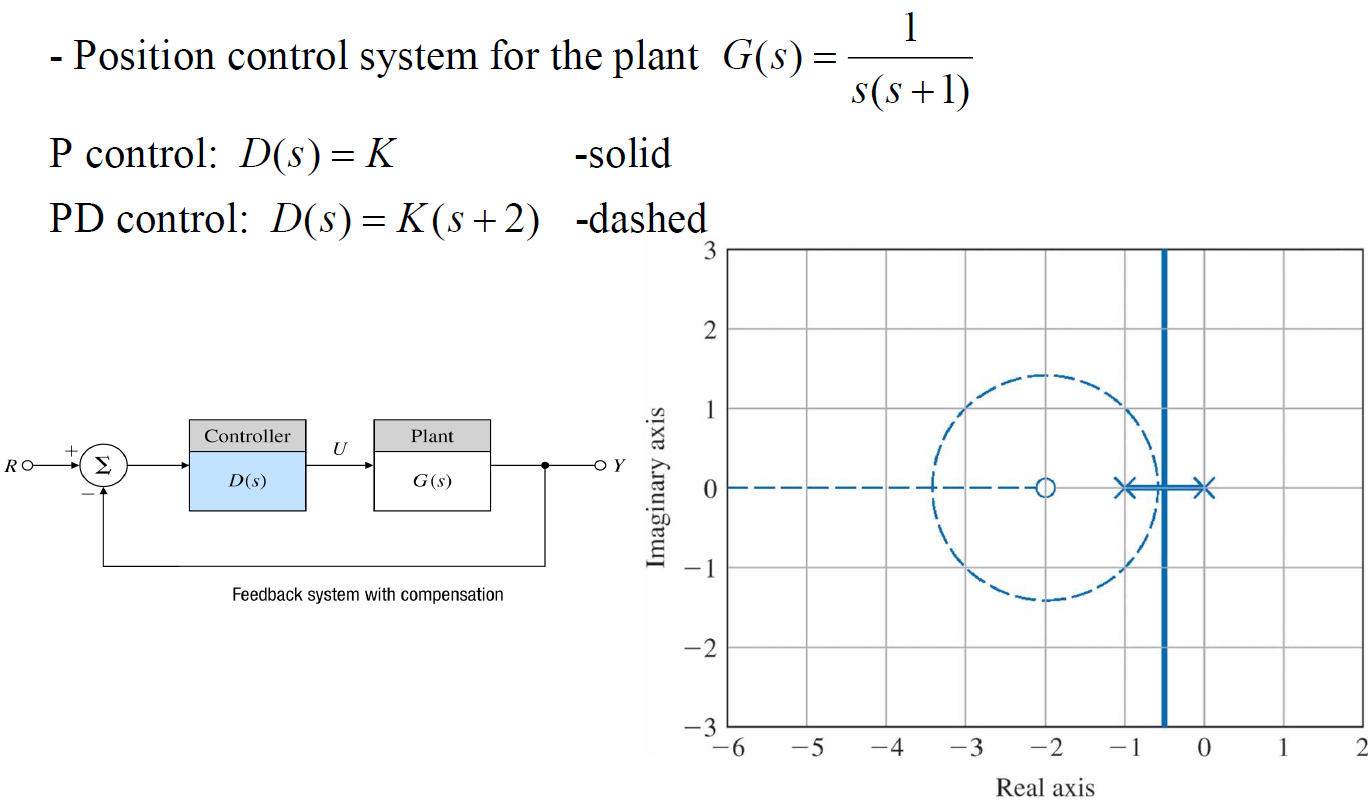
2-3. Lead compensator의 z, p 선정 방법
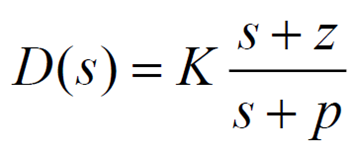
2-3-1. 방법 1 (z 먼저, p 나중)
- 를 과 가까운 곳에 위치 (사실상 일치)
- 를 의 5~20배 멀리 떨어뜨려라
2-3-2. 방법 2 (p 먼저, z 나중)
- 를 먼저 최대한 멀리 위치
- 원하는 pole을 정하고 그 pole이 있기 위한 zero 선정
여태까진 2개의 pole가지고만 시스템의 응답을 알아봤는데 추가된 zero의 영향이 있음을 인지해야한다.
ex) 방법 1
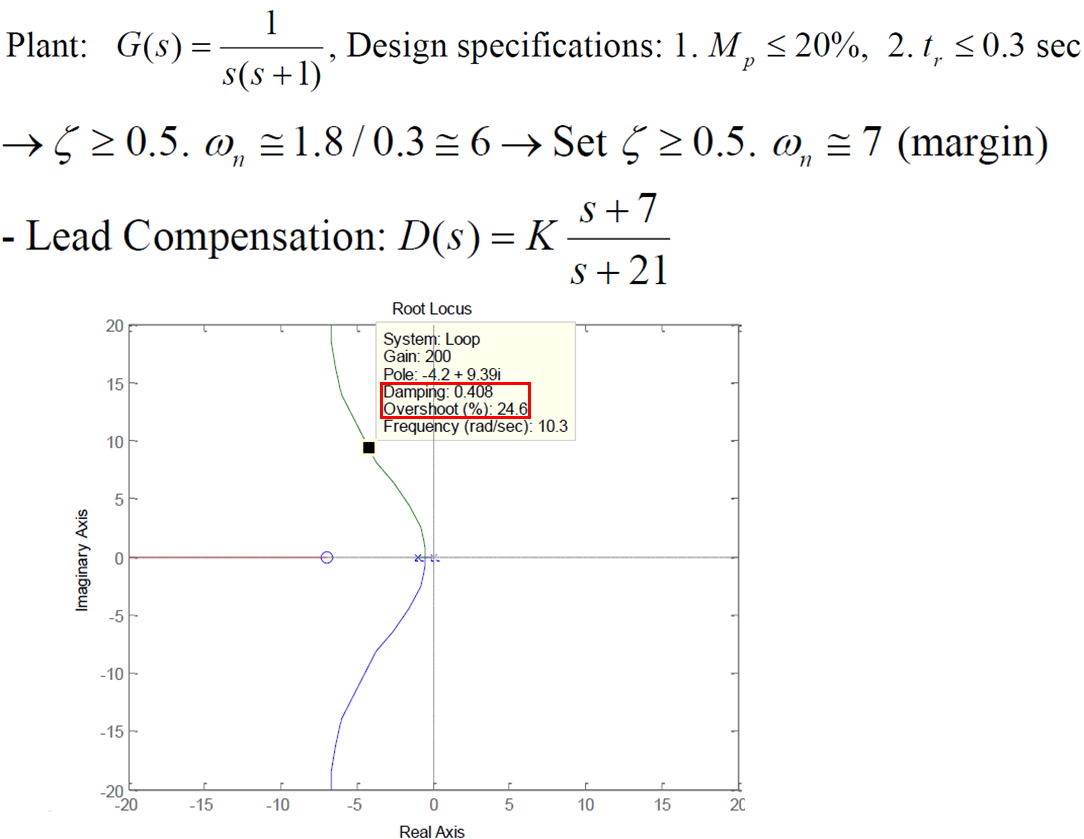
원하는 스펙 만족 X, pole 궤적이 더 밑으로 내려왔으면 좋겠음(감쇠 up) + p와 z가 서로 너무 가까움, 튜닝 필요
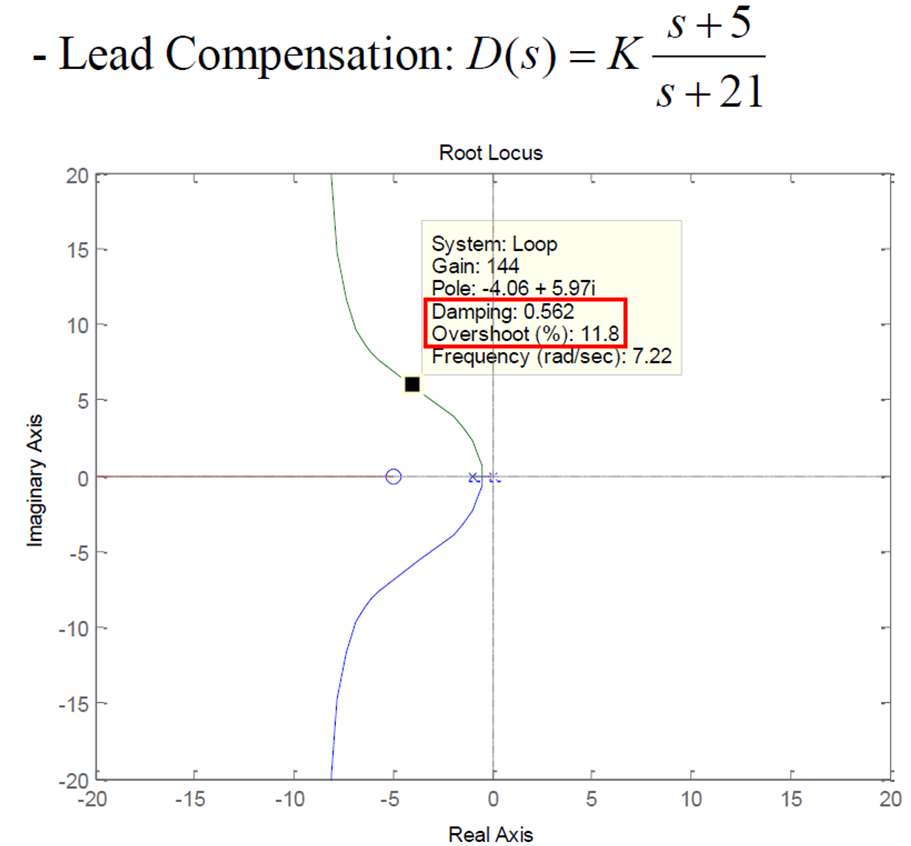
스펙 만족
ex) 방법 2
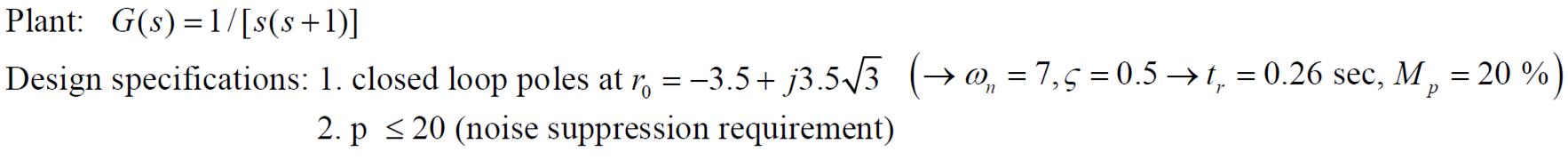
으로 결정, 가 되는 값 선정
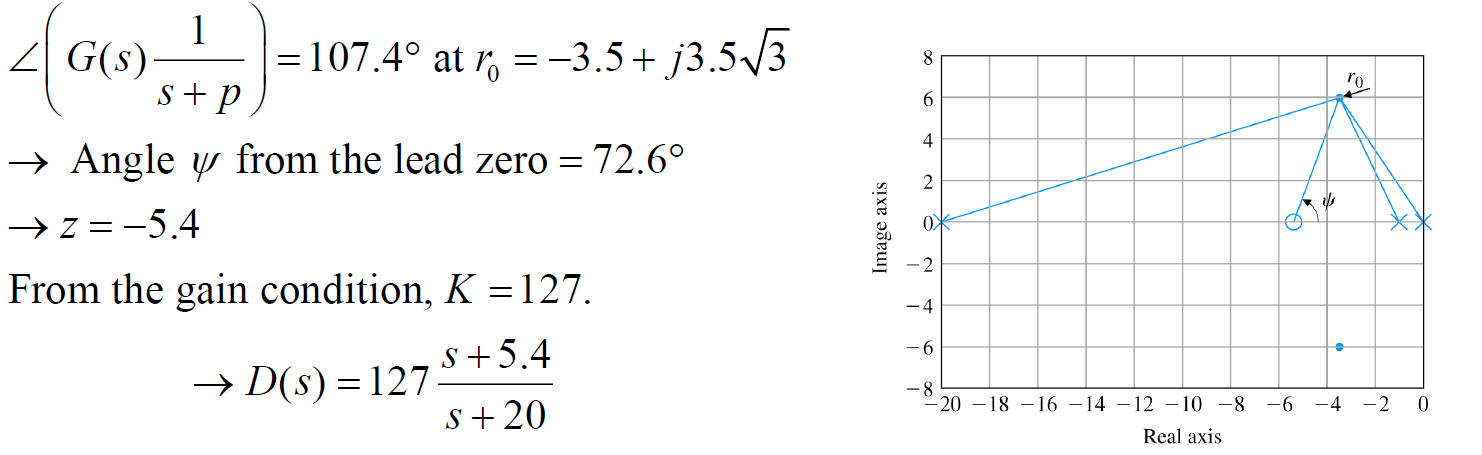
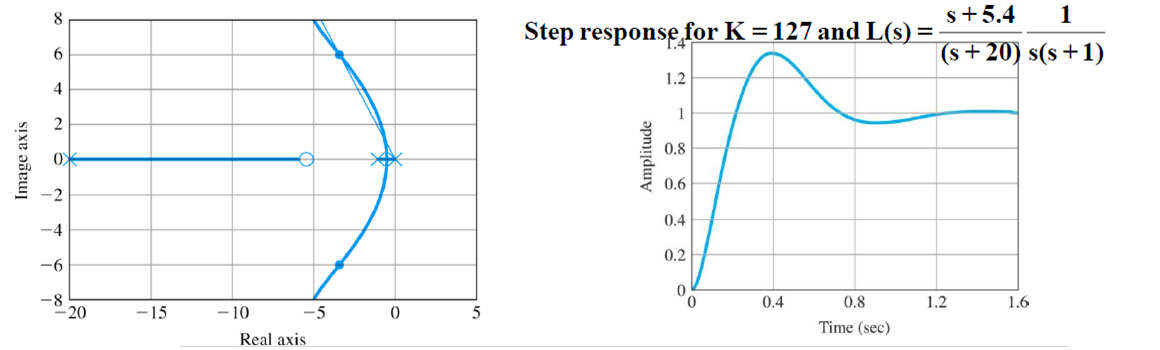
원하는 스펙에 맞지 않아 튜닝 필요
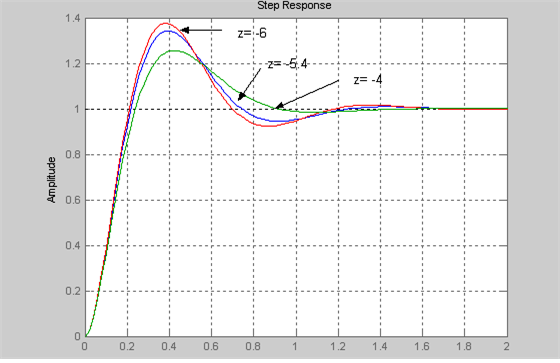
값을 조정해 튜닝
2-4. Lag compensation
- 응답은 잘 유지하면서
높은 주파수 영역에선 제어기가 거의 동작 x
Root Locus에 영향을 잘 끼치지 않으면서 주파수가 0일 때 DC gain()이 크길 희망
ex)
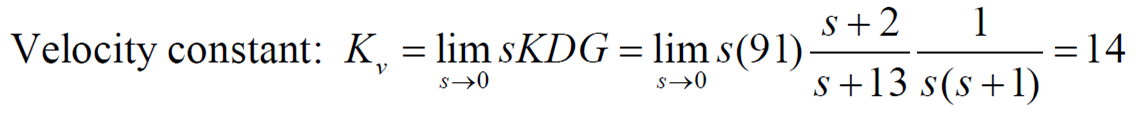
오차를 더 줄이고 싶어 원함 => 보상기 추가해
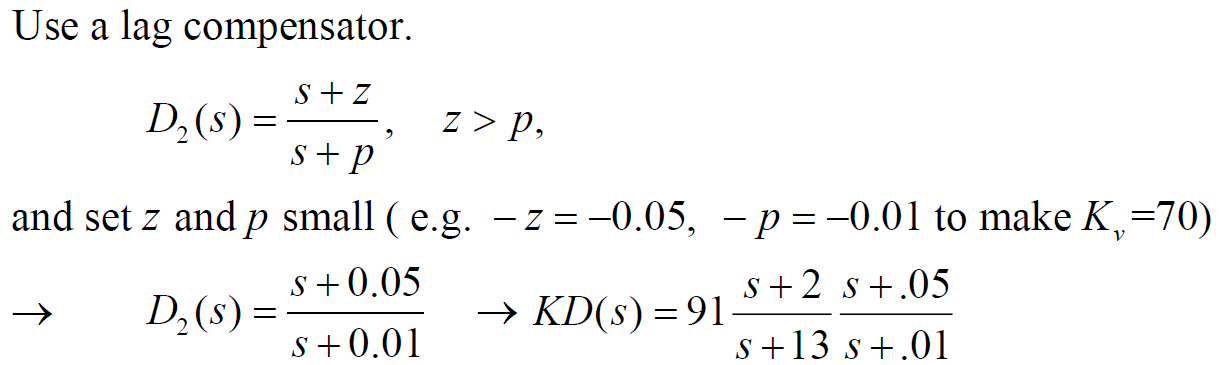
원점에 p, z 둘 다 매우 가까워서 Root Locus의 전체적인 모양 변형 x
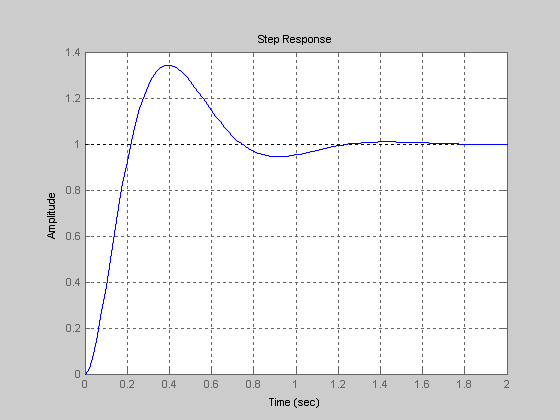
2-5. Notch compensation
ex)
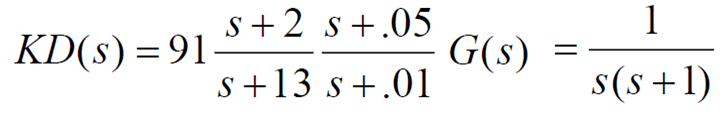
하지만 실제로는 이었고 nominal하게 시스템 모델링하는 과정에서 이란 빠진 부분이 숨겨져 있었다. 그래서 응답이 다음과 같이 나왔다.
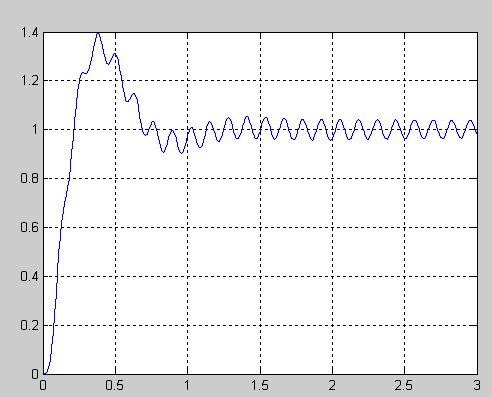
감쇠비가 에 비해 작아 진동 안 없어질 것
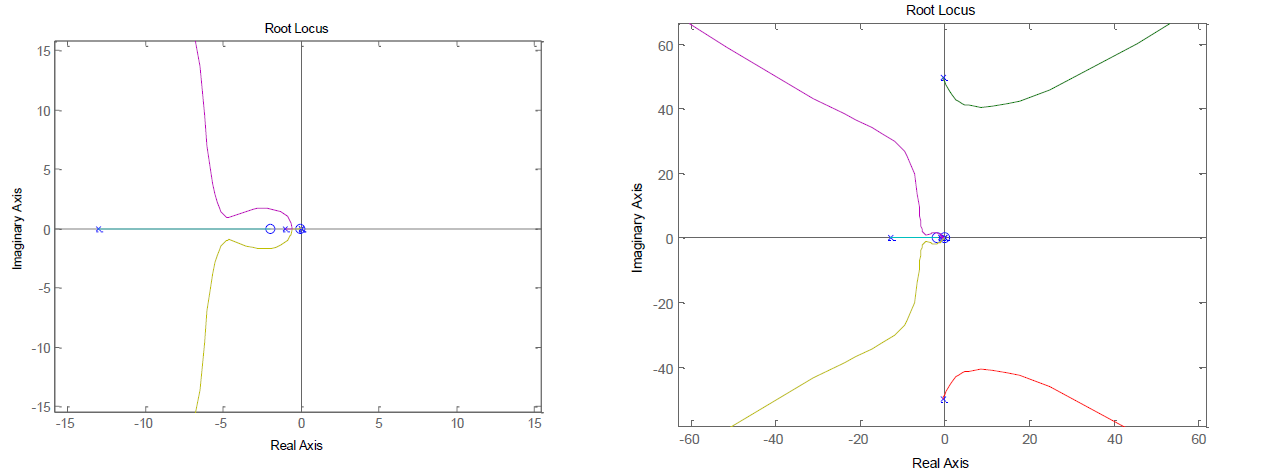
모르던 부분 때문에 시스템이 불안정
이를 해결하기 위해 2가지 방법 사용
2-5-1. Gain stabilization
- 영역일 때 loop gain()을 줄이면 그 영역에선 이 시스템에 미치는 영향 줄어 들 것
2-5-2. Phase stabilization
- 불안정하게 만드는 pole 근처에 zero를 추가해 수렴시켜 안정화
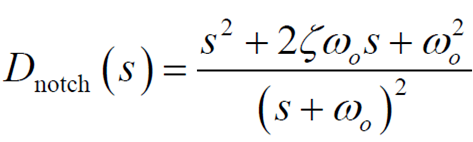
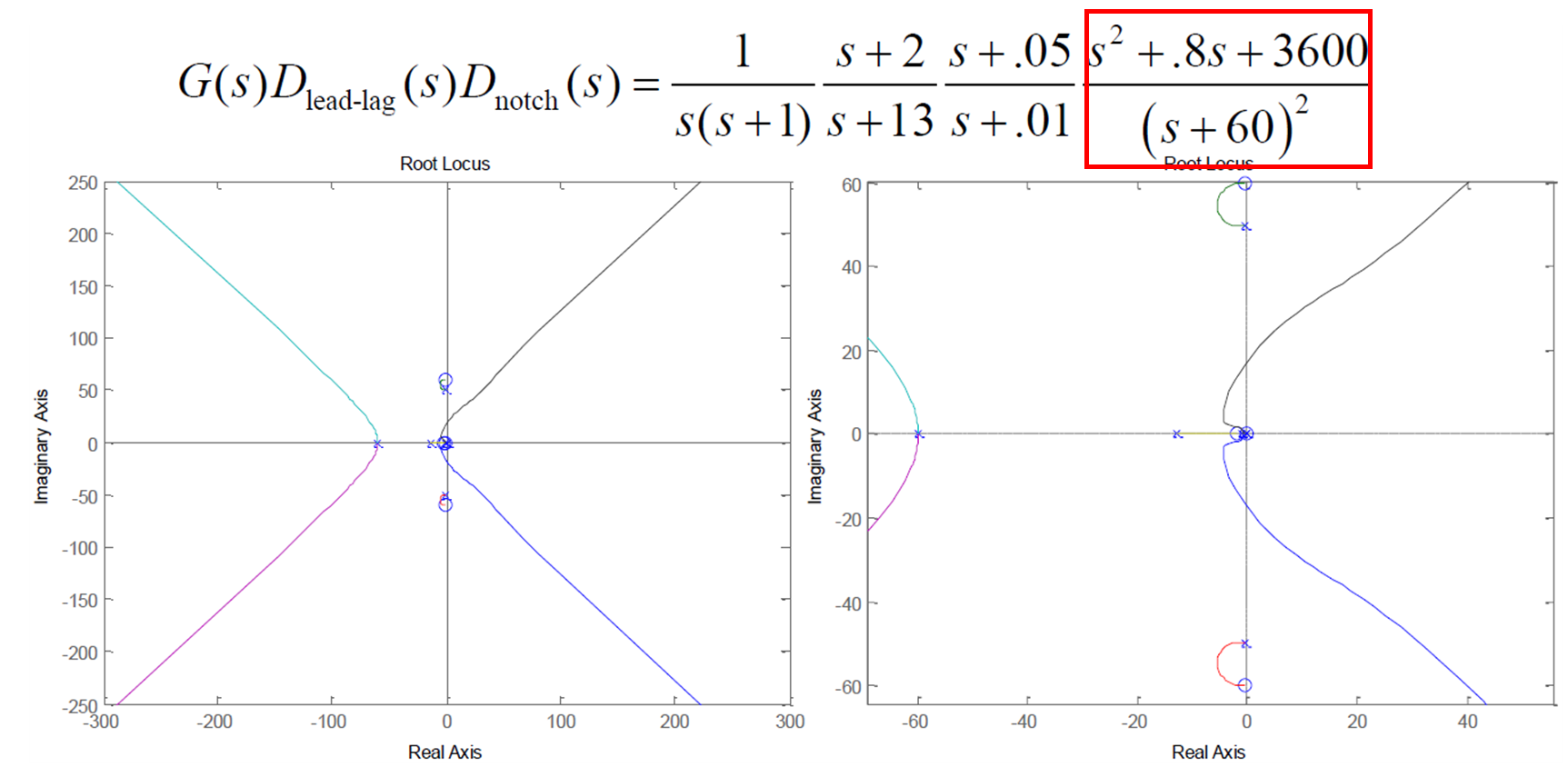
값이 너무 커지지만 않으면 안정적