복습문제

# 피처 값의 유형에 따라 새로운 피처를 추가해 고유값에 해당하는 칼럼에만 1, 나머지에는 0을 표시하는 방식
One - Hot 인코딩




items=['TV','냉장고',' 전자레인지','컴퓨터', '선풍기','선풍기',' 믹서','믹서'] 

# LabelEncoder
from sklearn.preprocessing import LabelEncoder
label_encoder = LabelEncoder()
label_encoder = label_encoder.fit_transform(items)
label_encoder 

# OneHotEncoder
from sklearn.preprocessing import OneHotEncoder
import numpy as np

items = np.array(items).reshape(-1, 1)
onehot_encoder = OneHotEncoder()
onehot_encoder = onehot_encoder.fit_transform(items)
onehot_encoder.toarray()



# StratifiedKFold 사용시 split() 메서드 인자에 레이블 데이터 셋도 포함해야 한다
O



# GridSearchCV(estimator, parm_grid = parmeters, scoring = 'accuracy', cv =)
estimator : classifier, regressor, pipeline 등이 사용될 수 있다.
param_grid : estimator의 튜닝을 위하여 파라미터, 사용될 파라미터를 dictionary 형태로 만들어서 넣는다.
scoring : 예측 성능을 측정할 평가 방법을 넣는다. 보통 accuracy 로 지정하여서 정확도로 성능 평가를 한다.
cv : 교차 검증에서 몇개로 분할되는지 지정한다.




# ()는 문자로된 레이블 값을 숫자값으로 일괄 변환함에 따라
# 숫자가 클수록 가중치가 더 부여되거나 중요하게 인식하는 등의 가능성이 발견되어
# 머신러닝 알고리즘에 적용할 경우 예측성능이 떨어질 수 있다
레이블 인코딩




# ()은 데이터의 분포가 가우시안 분포가 아닌 (혹은 분포를 알 수 없는) 경우 유용하다
정규화




# ()는이상치(극단적으로 크거나 작은값) 에 영향을 적게 받습니다
표준화




# GridSearchCV의 파라미터 'refit = True'는 어떤 옵션인가?
최적의 하이퍼 파라미터를 찾아서 재학습




# cross_val_score()은 내부적으로 StratifiedKFold를 사용하고 있다
O




# test data는 반드시 학습 데이터의 스케일링 기준에 다를 필요가 없으므로
# test data에 다시 fit을 적용해도 된다
x




from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import cross_val_score
from sklearn.datasets import load_iris

iris_data = load_iris()

dt_clf = DecisionTreeClassifier(random_state=42)
data = iris_data.data
label = iris_data.target
# corss_val_score() 사용
scores = cross_val_score(dt_clf, data, label, scoring = 'accuracy', cv = 3)




from sklearn.datasets import load_iris
import pandas as pd

iris = load_iris()
iris = iris['data']
iris_df = pd.DataFrame(iris) 
# pandas의 apply를 사용하여 정규화
iris_df.apply(lambda x:(x - x.min()) / (x.max() - x.min()))

# MinMaxScaler를 사용하여 정규화
from sklearn.preprocessing import MinMaxScaler

# iris_df.apply(lambda x:(x - x.min()) / (x.max() - x.min()))
scaler = MinMaxScaler()
iris_scaled = scaler.fit_transform(iris_df)
iris_df_scaled = pd.DataFrame(data = iris_scaled)




# 와인 데이터 가져오기
from sklearn.datasets import load_wine 
wine = load_wine()
features = X = _____
labels = y = _____
# 빈칸을 채우세요
features = X = wine.data
labels = y = wine.target
from sklearn.tree import DecisionTreeClassifier
# tree 를 가져오세요
df_clf = DecisionTreeClassifier()
# cross_val_score를 사용하며 4면 돌려주세요
from sklearn.model_selection import cross_val_score
cross_val_score(df_clf, X, y, scoring='accuracy', cv=4)




# narray 요소수 세기
np.bincount(labels)
> array([59, 71, 48], dtype=int64)
import collections, numpy
collections.Counter(labels)
> Counter({0: 59, 1: 71, 2: 48})
from collections import Counter
Counter(labels)
> Counter({0: 59, 1: 71, 2: 48})

---

(위키북스의 '파이썬 머신러닝 완벅 가이드' 개정 2판으로 공부하고 있습니다.)

타이타닉 생존자 예측(2)

데이터 전처리

데이터를 살펴보며 해줬던 전처리들을 한번에 모아 처리해주는 함수 transform_features(df) 를 만들어준다.

# Null 처리 함수
def fillna(df) :
    df['Age'].fillna(titianic_df['Age'].mean(), inplace = True)
    df['Cabin'].fillna('N', inplace = True)
    df['Embarked'].fillna('N', inplace = True)
    df['Fare'].fillna(0, inplace = True)
    return df

# 알고리즘에 불필요한 피처 제거
def drop_features(df) :
    df.drop(['PassengerId', 'Name', 'Ticket'], axis = 1, inplace = True)
    return df

# 레이블 인코딩 수행
def format_features(df) :
    df['Cabin'] = df['Cabin'].str[:1]
    features = ['Cabin', 'Sex', 'Embarked']
    for feature in features :
        le = LabelEncoder()
        le = le.fit(df[feature])
        df[feature] = le.transform(df[feature])
    return df

# 위에서 설정한 데이터 전처리 함수들을 모두 호출하겠다.
def transform_features(df) :
    df = fillna(df)
    df = drop_features(df)
    df = format_features(df)
    return df

이후 정답값이라 할 수 있는 Survived 속성만 별도로 분리해 클래스 결정값 데이터 셋으로 만들어준다.

# 데이터를 살펴보며 값이 변형되었을 수도 있기 때문에 데이터 재로딩
titianic_df = pd.read_csv('titanic_train.csv')

# feature data set와 data label set 추출
y_titanic_df = titianic_df['Survived']
x_titanic_df = titianic_df.drop('Survived', axis = 1)

X_titanic_df = transform_features(x_titanic_df)

train_test_split()

train data set을 기반으로 train_test_split()를 이용해 별도의 test data set을 추출한다. 비율은 20%로 한다.

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X_titanic_df, y_titanic_df, test_size = 0.2, random_state=11)

알고리즘을 이용한 생존자예측

머신러닝 알고리즘인 결정 트리, 랜덤 포레스트, 로지스틱 회귀를 이용해 생존자를 예측해본다.

from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score

# random_state = 11 / 예제를 수행할 때마다 같은 결과를 출력하기 위한 용도
# 결정트리 
dt_clf = DecisionTreeClassifier(random_state=11)
# random_Forest
rf_clf = RandomForestClassifier(random_state=11)
# 로지스틱 회귀
# solver='liblinear'
# 로지스틱 회귀의 최적화 알고리즘을 liblinear로 설정하겠다
# 일반적으로 작은 데이터 셋에서의 이진 분류에 좋은 성능
lr_clf = LogisticRegression(solver='liblinear')


# DecisionTreeClassifier
# 학습
dt_clf.fit(X_train, y_train)
# 예측
dt_pred = dt_clf.predict(X_test)
# 평가
print('DecisionTreeClassifier 정확도 : {0:.4f}'.format(accuracy_score(y_test, dt_pred)))


#random_Forest 학습/예측/평가
rf_clf.fit(X_train, y_train)
rf_pred = rf_clf.predict(X_test)
print('random_Forest 정확도 : {0:.4f}'.format(accuracy_score(y_test, rf_pred)))


# 로지스틱
lr_clf.fit(X_train, y_train)
lr_pred = lr_clf.predict(X_test)
print('로지스틱 정확도 : {0:.4f}'.format(accuracy_score(y_test, lr_pred)))

결과는 아래와 같다
DecisionTreeClassifier 정확도 : 0.7877
random_Forest 정확도 : 0.8547
로지스틱 정확도 : 0.8659

반복적인 행위를 하기 싫다면 함수로 만들어 for문으로 넣어줘도 될거 같았다.

def test(clf) :
    clf.fit(X_train, y_train)
    clf_pred = clf.predict(X_test)
    print('정확도 : {0:.4f}'.format(accuracy_score(y_test, clf_pred)))
    
for i in (dt_clf, rf_clf, lr_clf) :
    test(i)

# 정확도 : 0.7877
# 정확도 : 0.8547
# 정확도 : 0.8659

정확도가 이와같이 '로지스틱 회귀'가 다른 알고리즘에 비해 비교적 높게 나온것을 확인할 수 있었지만, 적은 데이터양으로 최적화 작업을 수행하지 않고 진행한 것이기 때문에 섣불리 평가할 수 없는 상태이다.

이제 교차검증으로 모델들을 추가적으로 평가해본다.

교차검증 : KFold

from sklearn.model_selection import KFold

# 폴드 셋이 5개인 KFold 객체를 생성
def exec_kfold(clf, folds = 5) :
    kfold = KFold(n_splits = folds)
    # 예측 결과 저장을 위한 리스트 객체 생성
    scores = []
    
    
    # KFold 교차 검증 수행
    for iter_count, (train_index, test_index) in enumerate(kfold.split(X_titanic_df)) :
        # X_titianic_df 데이터에서 교차 검증별로 학습과 검증 데이터를 가리키는 index 생성
        X_train, X_test = X_titanic_df.values[train_index], X_titanic_df.values[test_index]
        y_train, y_test = y_titanic_df.values[train_index], y_titanic_df.values[test_index]
        
        # Classifier 학습
        clf.fit(X_train, y_train)
        # 예측
        clf_pred = clf.predict(X_test)
        # 정확도 계산
        accuracy = accuracy_score(y_test, clf_pred)
        
        # 리스트에 담아주기
        scores.append(accuracy)
        print('교차검증 {0} 정확도 : {1:.4f}'.format(iter_count, accuracy))
        
    # 5개의 폴드에서 평균 정확도 계산
    mean_score = np.mean(scores)
    print('평균 정확도 : {0:.4f}'.format(mean_score))
    
# 호출
exec_kfold(dt_clf, folds = 5)

교차검증 0 정확도 : 0.7542
교차검증 1 정확도 : 0.7809
교차검증 2 정확도 : 0.7865
교차검증 3 정확도 : 0.7697
교차검증 4 정확도 : 0.8202
평균 정확도 : 0.7823

1차 정확도가 가장 높았던 '로지스틱 회귀'의 결과와 비슷하게 높았던 '랜덤포레스트'의 결과도 궁금해졌다.

print(exec_kfold(lr_clf, folds = 5))
print(exec_kfold(rf_clf, folds = 5))

# 로지스틱 결과
교차검증 0 정확도 : 0.7933
교차검증 1 정확도 : 0.7921
교차검증 2 정확도 : 0.7753
교차검증 3 정확도 : 0.7472
교차검증 4 정확도 : 0.8427
평균 정확도 : 0.7901

로지스틱 회귀의 경우 역시나 의사결정 트리에 비하여 조금 더 높게 나오기는 했지만 크게 차이를 보이지 않는 모습이 의외였고,

# 랜덤 포레스트
교차검증 0 정확도 : 0.7933
교차검증 1 정확도 : 0.8090
교차검증 2 정확도 : 0.8371
교차검증 3 정확도 : 0.7753
교차검증 4 정확도 : 0.8596
평균 정확도 : 0.8148

두 번째로 높은 결과를 보여줬던 랜덤 포레스트의 경우에는 평균 정확도만 봐도 확연하게 높은 모습을 보여줬다.

교차검증 : cross_val_score

from sklearn.model_selection import cross_val_score

scores = cross_val_score(dt_clf, X_titanic_df, y_titanic_df, cv = 5)

for i, accuracy in enumerate(scores) :
    print('교차검증 {0} 정확도 : {1:.4f}'.format(i, accuracy))
    
print('평균정확도 : {0:.4f}'.format(np.mean(scores)))

교차검증 0 정확도 : 0.7430
교차검증 1 정확도 : 0.7753
교차검증 2 정확도 : 0.7921
교차검증 3 정확도 : 0.7865
교차검증 4 정확도 : 0.8427
평균정확도 : 0.7879

cross_val_score와 KFold 의 평균정확도가 아주 약간이지만 다르다. 이는 cross_val_score가 StratifiedDFold를 이용하기 때문이다.

이것도 앞선 세 경우의 결과치가 궁금했기 때문에 함수로 묶어서 for문 돌려줘봤다.

from sklearn.model_selection import cross_val_score

def cross_val_score_test(clf) : 
    scores = cross_val_score(clf, X_titanic_df, y_titanic_df, cv = 5)
    for i, accuracy in enumerate(scores) :
        print('교차검증 {0} 정확도 : {1:.4f}'.format(i, accuracy))
    print('평균정확도 : {0:.4f}'.format(np.mean(scores)))

for j in  (dt_clf, rf_clf, lr_clf) :
    cross_val_score_test(j)
    print()



>
DecisionTreeClassifier(random_state=11) 의 결과입니다
교차검증 0 정확도 : 0.7430
교차검증 1 정확도 : 0.7753
교차검증 2 정확도 : 0.7921
교차검증 3 정확도 : 0.7865
교차검증 4 정확도 : 0.8427
평균정확도 : 0.7879

RandomForestClassifier(random_state=11) 의 결과입니다
교차검증 0 정확도 : 0.7933
교차검증 1 정확도 : 0.7978
교차검증 2 정확도 : 0.8483
교차검증 3 정확도 : 0.7640
교차검증 4 정확도 : 0.8652
평균정확도 : 0.8137

LogisticRegression(solver='liblinear') 의 결과입니다
교차검증 0 정확도 : 0.7877
교차검증 1 정확도 : 0.7921
교차검증 2 정확도 : 0.7753
교차검증 3 정확도 : 0.7640
교차검증 4 정확도 : 0.8202
평균정확도 : 0.7879

corss_val_score() 을 사용해줬을 때 역시! RandomForestClassifier의 결과가 가장 높게 나왔다. 잘 맞는 모델인가보다.

마지막으로 GridSearchCV를 이용하여 세 모델의 최적 하이퍼 파라미터를 찾아보자.

# cv = 5로 고정
# max_depth, min_samples_split, min_samples_leaf를 변경하면서 성능을 측정
from sklearn.model_selection import GridSearchCV

# 파라미터 설정
param = {
    'max_depth' : [2, 3, 5, 10],
    'min_samples_split' : [2, 3, 5], 
    'min_samples_leaf' : [1, 5, 8]
    }

# 함수 생성
def grid_clf(clf) :
    grid_clf = GridSearchCV(clf, param_grid = param, scoring='accuracy', cv = 5)
    grid_clf.fit(X_train, y_train)
    
    # 출력시 어떤 모델인지 확인하고 싶어서 추가
    s = str(clf).split('(')    
    print(f'{s[0]} 최적 하이퍼 파리미터 : ', grid_clf.best_params_)
    print(f'{s[0]} 최고 정확도 : ', round(grid_clf.best_score_, 4))
    best_clf = grid_clf.best_estimator_
    
    # GridSearchCV의 최적 하이퍼 파리미터로 학습된 Estimator로 예측 및 평가
    good_pred = best_clf.predict(X_test)
    accuracy = accuracy_score(y_test, good_pred)
    print('테스트 셋에서의 정확도 : {0:.4f}'.format(accuracy))
    

# 실행해보기....두근
for j in (dt_clf, rf_clf) :
    grid_clf(j)
    

    
>
DecisionTreeClassifier 최적 하이퍼 파리미터 :  {'max_depth': 3, 'min_samples_leaf': 5, 'min_samples_split': 2}
DecisionTreeClassifier 최고 정확도 :  0.7992
테스트 셋에서의 정확도 : 0.8715
RandomForestClassifier 최적 하이퍼 파리미터 :  {'max_depth': 5, 'min_samples_leaf': 1, 'min_samples_split': 2}
RandomForestClassifier 최고 정확도 :  0.8146
테스트 셋에서의 정확도 : 0.8827

의사결정트리와 랜덤포레스트만 돌린 결과이다. 비등하게 높았으나 RandomForestClasifier 가 조금 더 높은 것을 확인할 수 있다.

그런데 '로지스틱 회귀'의 경우 오류가 나는 것을 확인하였다. 왜일까...?

---

로지스틱 회귀

이름은 회귀인데 분류에 사용된다. 시그모이드 함수 = 로지스틱 함수

사용하는 파라미터 옵션값이 달라서 안되었던 것이다!!

params = {'penalty': ['l1', 'l2'], 'C': [0.01, 0.1, 1, 5, 10]}

lrc_grid = GridSearchCV(lr_clf, param_grid = params, scoring='roc_auc', cv = 5)
lrc_grid.fit(X_train, y_train)

print('최적 하이퍼 파라미터:', lrc_grid.best_params_)
print('최고 정확도 : {0:.4f}'.format(lrc_grid.best_score_))

best_lrc = lrc_grid.best_estimator_
# GridSearchCV의 최적 하이퍼 파리미터로 학습된 Estimator로 예측 및 평가
good_pred = best_lrc.predict(X_test)
accuracy = accuracy_score(y_test, good_pred)
print('테스트 셋에서의 정확도 : {0:.4f}'.format(accuracy))

최적 하이퍼 파라미터: {'C': 5, 'penalty': 'l1'}
최고 정확도 : 0.8444
테스트 셋에서의 정확도 : 0.8547

속이 시원하넹

---

정확도(Accuracy)

실제 데이터에서 예측 데이터가 얼마나 같은지를 판단하는 지표

			예측 결과가 동일한 데이터의 건수
Accuracy = --------------------------------
			   전체 예측 데이터 건수

직관적으로 모델 예측 성능을 나타내는 평가 지표이다. 하지만 이진 분류의 경우 데이터 구성에 따라 성능을 왜곡하는 지표가 될수도 있음

전체 데이터에서 0이 98%를 차지하는 훈련데이터로 모델의 성능을 99%까지 끌어올린다고 하더라도, 이 모델이 1을 제대로 구분할 수 있을지 신뢰할 수 없다는 말이다.

이렇듯 편향적이고 불균형한 label data set으로 구한 정확도는 성능 수치로 사용할 수가 없다. 이러한 한계점을 극복하기 위해 여러가지 분류 지표를 함께 적용하여 머신러닝의 모델 성능을 평가해야한다.

오차행렬(혼동 행렬, Confusion Matrix)

이진분류에서는 주로 오차행렬을 통해 성능을 평가하게 된다. 오차행렬은 모델의 예측이 얼마나 헷갈리고 있는지 보여주는 유용한 지표가 된다.

TN : True Negative, 예측 결과가 정답과 일치(True)하고, 실제 레이블이 negative(0)인 경우
TP : True Positive, 예측 결과가 정답과 일치(True)하고, 실제 레이블이 positive(1)인 경우
FP : False Positive, 예측 결과가 정답과 불일치(False)하고, 실제 레이블이 negative(0)인 경우
FN : False Negtive, 예측 결과가 정답과 불일치(False)하고, 실제 레이블이 positive(1)인 경우

※ T/F 값은 예측값과 실제값이 같다/틀리다
※ N/P 는 예측 결과값

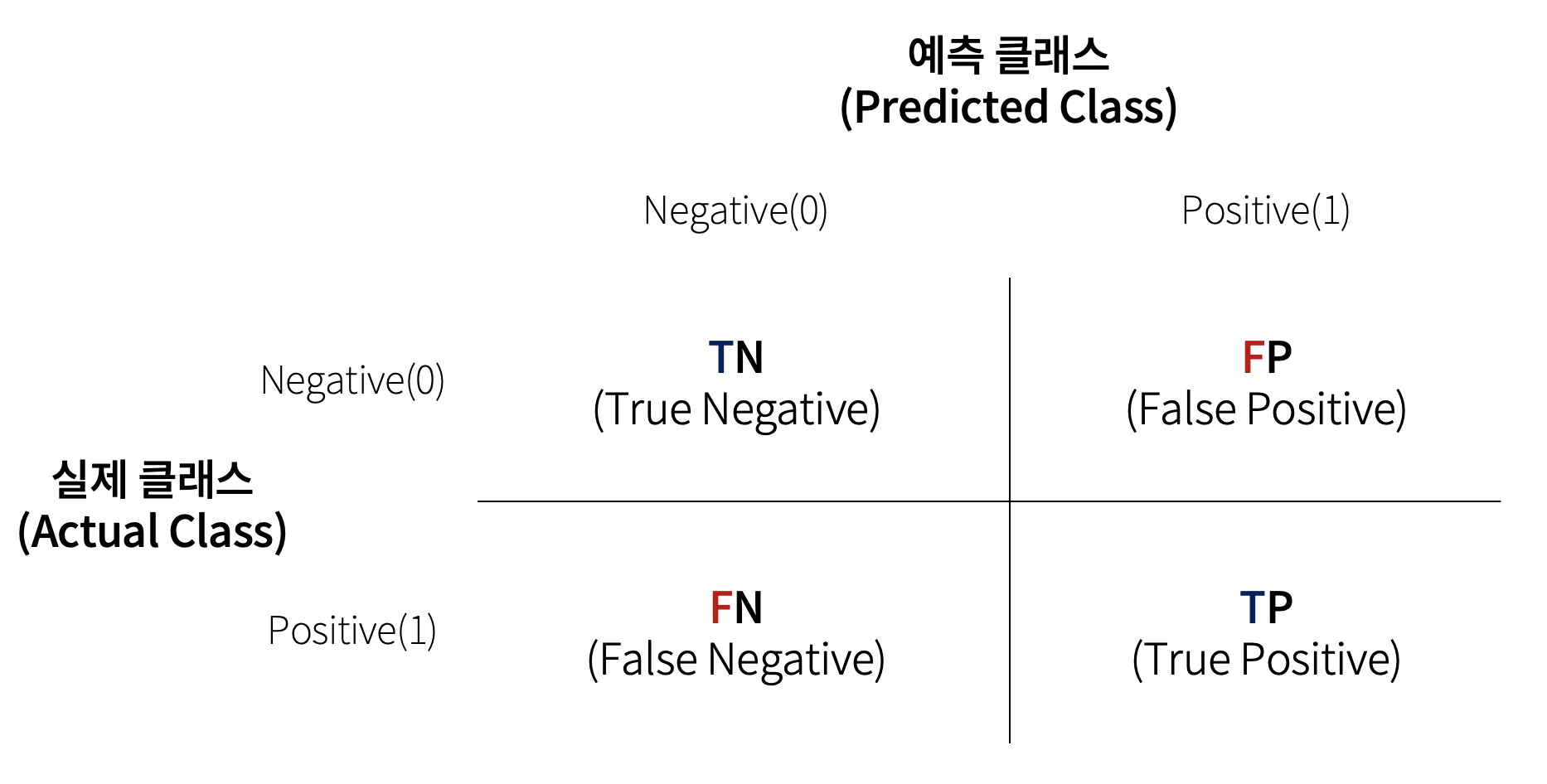
위는 분류기의 성능을 여러 방면으로 판단할 수 있는 기반 정보를 제공한다. 이 값들을 조합해 정확도(Accuracy), 정밀도(Precision), 재현도(Recall) 값을 알 수 있기 때문이다.

정확도는 예측값과 실제 값이 얼마나 동일한가에 대한 비율만으로 계산되기 때문에 오차 행렬에서 True에 해당하는 TN과 TP에 매우 많이 좌우된다.

불균형한 데이터 세트에서 정확도보다 더 선호되는 평가 지표는 정밀도(Precision)와 재현율(Recall)이다.

from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score, confusion_matrix

print(len(y_test), len(rf_pred))
# 179 179

# 혼동행렬 만들어보기
confusion_matrix(y_test, rf_pred)
# array([[107,  11],
#        [ 15,  46]], dtype=int64)


# 정확도 비교
# accuracy_score() 사용
accuracy_score(y_test, rf_pred)
# 0.8547486033519553

# 혼동행렬에서 나온 값으로 계산
(107+46) / (107+11+15+46)
# 0.8547486033519553

---

정밀도(Precision) / 재현율(Recall)

정밀도 : 모델이 Positive로 예측(FP+TP) 중에 실제 값이 Positive인 경우(TP) 의 비율로 Positive 예측의 성능을 더욱 정밀 측정하기 위한 평가 지표

					   TP
Precision = 정밀도 = --------
					 FP + TP

재현율 : 실제 값이 Positive인 경우(FN+TP) 중에 모델의 예측이 Positive로 일치한 경우(TP)의 비율

				   TP
Recall = 재현율 = --------
				 FN + TP

재현율 과 정밀도는 모두 동일하게 TP를 높이는데 초점을 두고 있지만 재현율은 FN(실제 Positive, 예측 Negative)를 낮추는 곳에, 정밀도는 FP(예측 불일치False하고, 실제 negative)를 낮추는 데에 초점을 맞추고 있다.
→ 이 같은 특성때문에 서로 보완적인 지표로서 분류의 성능을 평가하는 데 적용된다. 가장 좋은 성능 평가는 재현율과 정밀도 모두 높은 수치를 얻는 것.

정밀도/재현율 Trade-off

정밀도와 재현율은 상호 보완적인 평가 지표이기 때문에 어느 한쪽을 강제로 높인다면 다른 한쪽의 수치는 떨어지기 쉬운데 이를 트레이드오프(Trade-off)라 한다.

임계값의 변화는 정밀도와 재현율에 영향을 끼치는데, 낮아질수록 positive로 분류할 확률이 높아지기 때문에 재현율 값이 높아진다. Positive 예측을 많이 하다보니 실제 Positive를 Negative로 예측(FN)하는 횟수가 줄어들기 때문, 반면 실제 Negative를 Positive라고 판단(FP)하는 횟수가 늘어나기 때문에 정밀도는 떨어지게 된다.

이처럼 정밀도와 재현율 성능수치를 한쪽만 참조한다면 극단적으로 수치 조작이 가능하다. 수치가 적절하게 조합되어 분류의 종합적인 성능 평가에 사용될 수 있는 평가 지표가 필요

위에서 사용하던 타이타닉 데이터를 이용하여 예시를 보겠다.

# 오차행렬, 정확도, 정밀도, 재현율을 한꺼번에 계산하는 함수 생성
from sklearn.metrics import accuracy_score, precision_score , recall_score , confusion_matrix
def get_clf_eval(y_test , pred):
    # 오차행렬
    confusion = confusion_matrix( y_test, pred)
    # 정확도
    accuracy = accuracy_score(y_test , pred)
    # 정밀도
    precision = precision_score(y_test , pred)
    # 재현율
    recall = recall_score(y_test , pred)
    print('오차 행렬')
    print(confusion)
    print('정확도: {0:.4f}, 정밀도: {1:.4f}, 재현율: {2:.4f}'.format(accuracy , precision ,recall))
    print()




# 임계값을 0.4에서 0.6까지 0.05씩 증가시키며 평가 지표 조사
# 테스트를 수행할 모든 임곗값을 리스트 객체로 저장. 
thresholds = [0.4, 0.45, 0.50, 0.55, 0.60]

from sklearn.preprocessing import Binarizer
def get_eval_by_threshold(y_test , pred_proba_c1, thresholds):
    for custom_threshold in thresholds:
        # Binarizer()는 threshold보다 작거나 같으면 0, 크면 1을 반환한다.
        binarizer = Binarizer(threshold=custom_threshold).fit(pred_proba_c1) 
        
        # binarizerf를 이용하여 transform(fit은 해주지 않는다.)
        custom_predict = binarizer.transform(pred_proba_c1)
        print('임곗값:', custom_threshold)
        get_clf_eval(y_test , custom_predict)        


# predict_proba( ) 를 통하여 개별 레이블별 예측확률을 반환받을 수 있다
# 반환되는 ndarraysms 첫번째 칼럼이 클래스 값 0에 대한 예측확률
# 두번째 칼럼이 클래스 값 1에 대한 예측확률이다
pred_proba = lr_clf.predict_proba(X_test)
get_eval_by_threshold(y_test ,pred_proba[:,1].reshape(-1,1), thresholds )

임곗값: 0.4
오차 행렬
[[99 19]
 [13 48]]
정확도: 0.8212, 정밀도: 0.7164, 재현율: 0.7869

임곗값: 0.45
오차 행렬
[[108  10]
 [ 14  47]]
정확도: 0.8659, 정밀도: 0.8246, 재현율: 0.7705

임곗값: 0.5
오차 행렬
[[109   9]
 [ 14  47]]
정확도: 0.8715, 정밀도: 0.8393, 재현율: 0.7705

임곗값: 0.55
오차 행렬
[[111   7]
 [ 16  45]]
정확도: 0.8715, 정밀도: 0.8654, 재현율: 0.7377

임곗값: 0.6
오차 행렬
[[112   6]
 [ 17  44]]
정확도: 0.8715, 정밀도: 0.8800, 재현율: 0.7213

책과는 다르게 임계값이 0.5인 경우가 적당해보인다. (정확도와 정밀도가 올랐고 재현율은 0.55보다 낮고 0.45와 같다)

F1 Score

정밀도와 재현율을 결합한 지표이다. 둘 중 어느 한쪽으로 치우치지 않는 수치를 나타낼때 상대적으로 높은 값을 가지며, 정밀도와 재현율의 조화 평균으로 계산된다.

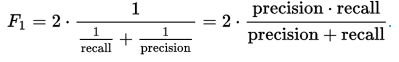
타이타닉 생존자 예측에서 인계값을 변화시키며 F1 스코어를 포함한 평가 지표를 구해보자. 앞서 작성한 get_clf_eval() 함수에 F1 스코어를 구하는 로직을 추가한 후 get_eval_by_threshold() 함수를 통해 임계값 0.4~0.6 별로 정확도와 정밀도, 재현율, F1스코어를 본다.

# 오차행렬, 정확도, 정밀도, 재현율을 한꺼번에 계산하는 함수 생성
from sklearn.metrics import accuracy_score, precision_score , recall_score , confusion_matrix
def get_clf_eval(y_test, pred) :
    confusion = confusion_matrix(y_test, pred)
    accuracy = accuracy_score(y_test, pred)
    precision = precision_score(y_test, pred)
    recall = recall_score(y_test, pred)
    
    # F1 스코어 추가
    f1 = f1_score(y_test, pred)
    print('오차행렬')
    print(confusion)
    
    # f1 score print
    print('정확도 : {0:.4f}, 정밀도:{1:.4f}, 재현율 : {2:.4f}, F1:{3:.4f}'.format(accuracy, precision, recall, f1))
    print()
    
thresholds = [0.4, 0.45, 0.50, 0.55, 0.60]
pred_proba = lr_clf.predict_proba(X_test)
get_eval_by_threshold(y_test, pred_proba[:,1].reshape(-1, 1), thresholds)

임곗값: 0.4
오차행렬
[[99 19]
 [13 48]]
정확도 : 0.8212, 정밀도:0.7164, 재현율 : 0.7869, F1:0.7500

임곗값: 0.45
오차행렬
[[108  10]
 [ 14  47]]
정확도 : 0.8659, 정밀도:0.8246, 재현율 : 0.7705, F1:0.7966

임곗값: 0.5
오차행렬
[[109   9]
 [ 14  47]]
정확도 : 0.8715, 정밀도:0.8393, 재현율 : 0.7705, F1:0.8034

임곗값: 0.55
오차행렬
[[111   7]
 [ 16  45]]
정확도 : 0.8715, 정밀도:0.8654, 재현율 : 0.7377, F1:0.7965

임곗값: 0.6
오차행렬
[[112   6]
 [ 17  44]]
정확도 : 0.8715, 정밀도:0.8800, 재현율 : 0.7213, F1:0.7928

위에서 했던 예상과 같이 임계값이 0.5일때 F1 스코어가 가장 좋은 값을 보여주고 있다. 기분좋다

---

ROC 곡선과 AUC

ROC 곡선

• Receiver Operation Characteristic Curve
• 우리말로 '수신자 판단 곡선' 이라는 이상한 이름
• 의학분야에서 많이 사용하며 머신러닝에서는 지표로 많이 사용된다.
• FPR(False Positive Rate)가 변할 때 TPR(True Positive Rate)가 어떻게 변하는지를 나타내는 지표이다.
  → FPR값이 x축 / TPR값이 y축이 된다.

TPR

• True Positive Rate
• 재현율, 민감도
• 실제 Positive TP+FN 중 모델이 올바르게 분류한 TP의 비율을 의미한다 (TP/(FN+TP))
• 이에 대응하는 지표로 TNR(Ture Negative Rate)라고 불리는 특이성(Specificity)이 있다. 이 특이성은 실제 Negative FP+TN 중 모델이 올바르게 Negative로 분류한 TN의 비율을 의미한다.
  → FPR = FP / (FP+TN) = 1 - TNR
  ∴ 1 - 특이성 으로도 표현 가능하다.

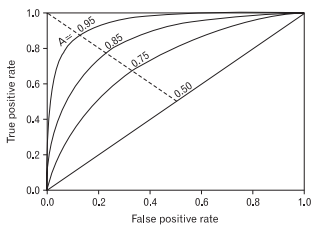
ROC곡선을 살펴보면 (가운데 직선인) 0.5 값은 동전을 무작위로 던져 앞/뒤를 맞추는 랜덤수준의 이진 분류 ROC 직선으로 최저값이다. 이처럼 ROC곡선은 가운데 직선에 가까울 수록 성능이 떨어지는 것으로 보고, 멀어질 수록 성능이 좋은 것이라고 본다.

FPR을 0부터 1까지 점진적으로 증가하면서 TPR의 변화 값을 구해 그리는데, 임계값(Threshold)값을 변화시키며 수행할 수 있다.
→ 0으로 지정하면 TN 값이 0이 되기 때문에 FPR값은 1이 된다. 이렇게 하면 분류기의 Positive 확률 기준이 너무 낮아져 모두 Positive 로 예측한다.
→ 1로 지정하면 TN값이 1이 되기 때문에 분류기의 기준이 너무 높아져 데이터를 Postive로 예측할 수 없다. 이에 따라 FPR값은 0이 된다.

일반적으로 ROC 곡선 자체는 FPR과 TPR의 변화값을 보는데만 이용하고 사실상 분류 성능의 지표로 사용되는 것은 ROC 곡선 면적에 기반한 AUC(Area Under Curve) 값이다. AUC 값은 ROC 곡선 밑의 면적을 계산한 것으로 일반적으로는 1에 가까워지면 좋은 성능수치를 얻게 된다.
→ AUC 값이 높으려면 FPR이 얼마나 작은 상태에서 큰 TPR을 얻을 수 있는지가 관건

예시로 roc_curve()를 이용해 타이타닉 생존자 예측 모델의 FPR, TPR, 임계값을 구해보자

from sklearn.metrics import roc_curve

# Positive 확률
lr_pred_proba_po = lr_clf.predict_proba(X_test)[:,1].reshape(-1,1)

# FPR(1-특이도), TPR(재현율=민감도), Threshold
# 임계값이 큰 값부터 작은 값 순서이다.
FPRs, TPRs, thresholds = roc_curve(y_test, lr_pred_proba_po)
print("임계값 배열:", thresholds.shape)

# 일부 threshold만 사용
# roc_curve에서 thresholds[0]은 max(예측확률)+1로 임의 설정된다. 이를 제외하기 위해 np.arange는 1부터 시작
thr_idx = np.arange(1, thresholds.shape[0], 10)

print("샘플 추출을 위한 배열의 index : ", thr_idx)
print("샘플 index로 추출한 임계값:", np.round(thresholds[thr_idx],2))
print("샘플 임계값별 FPR:", np.round(FPRs[thr_idx],3))
print("샘플 임계값별 TPR:", np.round(TPRs[thr_idx],3))


>
임계값 배열: (51,)
샘플 추출을 위한 배열의 index :  [ 1 11 21 31 41]
샘플 index로 추출한 임계값: [0.95 0.64 0.4  0.22 0.13]
샘플 임계값별 FPR: [0.    0.042 0.161 0.322 0.669]
샘플 임계값별 TPR: [0.016 0.656 0.787 0.902 0.967]

roc_curve()를 이용하여 임계값별 FPR과 TPR을 구했다.

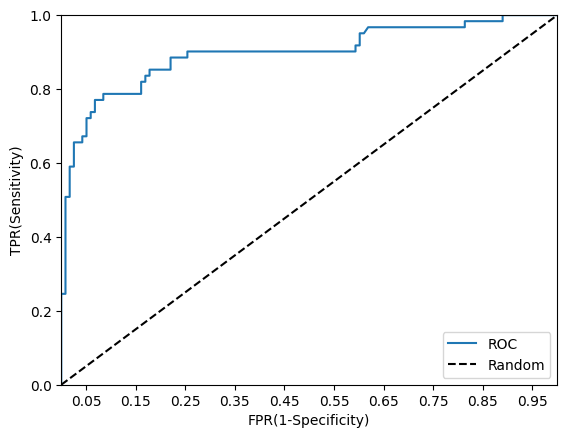
def roc_curve_plot(y_test, pred_proba_po):
    # FPR(1-특이도), TPR(재현율=민감도), Threshold
    # precision_recall_curve와는 다르게 임계값이 큰 값부터 작은 값 순서이다.
    FPRs, TPRs, thresholds = roc_curve(y_test, pred_proba_po)
    
    # ROC 곡선을 그래프 곡선으로 그린다
    plt.plot(FPRs, TPRs, label ="ROC")
        
    # 기준값(?인 가운데 대각선 직선을 그린다
    plt.plot( [0,1], [0,1], "k--", label="Random")
    
    # x축 스케일 0.1 단위로 조정
    start, end = plt.xlim()
    plt.xticks( np.round( np.arange(start, end, 0.1), 2))
    
    # 기타 옵션
    plt.xlim(0,1), plt.ylim(0,1)
    plt.xlabel("FPR(1-Specificity)"), plt.ylabel("TPR(Sensitivity)")
    plt.legend()
    
    # 그래프 보기
    plt.show()
    
# Positive 확률
lr_pred_proba_po = lr_clf.predict_proba(X_test)[:,1].reshape(-1,1)
roc_curve_plot(y_test, lr_pred_proba_po)