[제어공학] Z-Transform

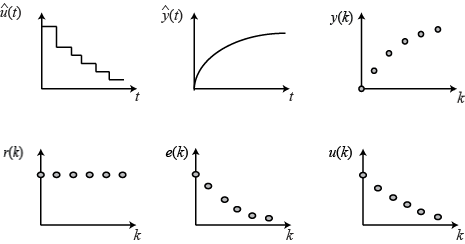
우리가 단순히 계산만 하여 제어공학 이론을 공부한 것과는 다르게 실무에서는 $\mu C$(micro controller)와 같은 디지털 제어 장치에 의존하여 제어를 하게 됩니다. 따라서 analog 값을 그대로 읽지 못하고 $A/D$Converter와 같은 부품을 이용하여 디지털 장치가 이해할 수 있는 discrete한 형태로(그림 아랫줄 참고) 데이터를 받아들이게 됩니다.
이 경우에는 기존에 Laplace-Transform을 기반으로 한 주파수 해석과는 조금 달라지게 되는데, 이러한 문제를 해결할 수 있는 z-transform에 대하여 배워 보겠습니다.

Zero order hold equivalent (zoh)

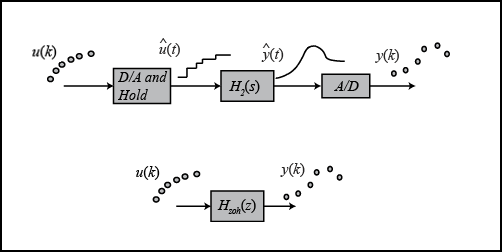
$\mu C$에서 처리하는 데이터는 $u(k)$와 같이 discrete한 데이터입니다. 점과 점 사이의 값을 알 수 없기 때문에 상수값으로 근사하여 $\hat u(t)$와 같은 형태로 만듦니다.
이를 Zero order hold equivalent라고 합니다.

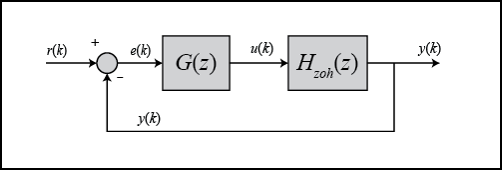
$e_k$와 $e_{k-1}$ 사이의 시간 간격을 sampling time이라고 합니다. 물론 짧을 수록 성능이 좋아지겠지만, 그만큼 연산이 많아지기 때문에 trade-off가 존재합니다.

matlab에서는 c2d(continuous to digital) 함수를 통하여 쉽게 연속 전달 함수를 이산 전달 함수로 바꿀 수 있습니다.

s = tf('s');
G = 40/s/(s+2);
c2d(G, 0.01, 'zoh') % c2d(tf, sampling time, method)

ans =
  0.001987 z + 0.001974
  ---------------------
  z^2 - 1.98 z + 0.9802
샘플 시간: 0.01 seconds
이산시간 전달 함수입니다

Z-Transform

연속 신호에서의 Differntial Equation(미분방정식)를 쉽게 풀 수 있었던 Laplace-Transform과 반대로 이산 시간에서의 Difference Equation(차분 방정식)을 쉽게 풀 수 있는 방법은 Z-Transform입니다. 일종의 Discrete Time Fourier Transform입니다.

기본적인 정의는 다음과 같습니다.

다음과 같은 수열이 있다고 합니다.
$f(0), f(1), \dots,f(k)$

• Two sided z-transform
  $Z\{f(k)\}=F(z)=\displaystyle\sum_{n=-\infin}^{\infin}f(k)z^{-k}$
• One sided z-transform
  $\{f(k)\}=F(z)=\displaystyle\sum_{n=0}^\infin f(k)^{-k}$

우리는 음의 시퀀스는 사용하지 않기 때문에 One sided z-transform을 사용합니다.
그리고 time delay에 대하여 다음과 같은 특징이 있습니다.

$\begin{aligned} Z\{f(k-m)\}&=\displaystyle\sum_{k=0}^\infin f(k-m)z^{-k}\\ &=\displaystyle\sum_{k=0}^\infin f(k')z^{-k'-m} (\because k-m=k')\\ &=z^{-m}\displaystyle\sum_{k=0}^\infin f(k')z^{-k'}\\ &=z^{-m}F(z) \end{aligned}$