만약 시스템이 제어가능하고 관측가능하다면, 성능사양을 만족시킬 수 있는 모든 원하는 위치에 모든 극점을 배치할 수 있습니다. 하지만 일반적으로 어떤 시스템의 상태를 완전히 모두 관측한다는 것은 불가능합니다. 그래서 후에 observer라는 개념이 추가로 도입됩니다. 순서대로 알아보겠습니다.
Full-state feedback control law
용어
State Variable: 시스템의 상태를 정의할 수 있는 최소한의 독립변수들입니다.(≈ \approx ≈
[ x 1 ( t ) x 2 ( t ) … x n ( t ) ] \begin{bmatrix}x_1(t)&x_2(t)&\dots&x_n(t)\end{bmatrix} [ x 1 ( t ) x 2 ( t ) … x n ( t ) ]
State Vector: 상태 변수들의 벡터로 표현한 것입니다.
x ⃗ ( t ) = [ x 1 ( t ) x 2 ( t ) ⋮ x n ( t ) ] u ⃗ ( t ) = [ u 1 ( t ) u 2 ( t ) ⋮ u m ( t ) ] y ⃗ ( t ) = [ y 1 ( t ) y 2 ( t ) ⋮ y p ( t ) ] \vec x(t)=\begin{bmatrix}x_1(t)\\x_2(t)\\\vdots\\x_n(t)\end{bmatrix}\quad\quad\quad\quad \vec u(t)=\begin{bmatrix}u_1(t)\\u_2(t)\\\vdots\\u_m(t)\end{bmatrix}\quad\quad\quad\quad \vec y(t)=\begin{bmatrix}y_1(t)\\y_2(t)\\\vdots\\y_p(t)\end{bmatrix} x ( t ) = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ x 1 ( t ) x 2 ( t ) ⋮ x n ( t ) ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ u ( t ) = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ u 1 ( t ) u 2 ( t ) ⋮ u m ( t ) ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ y ( t ) = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ y 1 ( t ) y 2 ( t ) ⋮ y p ( t ) ⎦ ⎥ ⎥ ⎥ ⎥ ⎤
State Space Model: 시스템은 두 개의 상태방정식으로 표현됩니다.x ⃗ ( t ) \vec x(t) x ( t ) y ⃗ ( t ) \vec y(t) y ( t ) u ⃗ ( t ) \vec u(t) u ( t ) A n × n A_{n\times n} A n × n B n × m B_{n\times m} B n × m C p × n C_{p\times n} C p × n D p × m D_{p\times m} D p × m \\
x ˙ = A x ( t ) + B u ( t ) y ( t ) = C x ( t ) + D u ( t ) \begin{aligned} \dot x&=Ax(t)+Bu(t)\\ y(t)&=Cx(t)+Du(t)\end{aligned} x ˙ y ( t ) = A x ( t ) + B u ( t ) = C x ( t ) + D u ( t )
예제
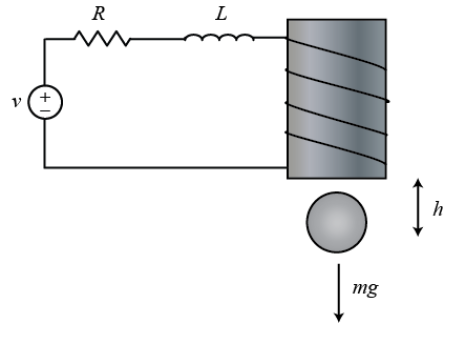
일반적으로 사용하는 질량-스프링-댐퍼 시스템과는 조금 다른 시스템으로 모델링 하여 보겠습니다.
m = 0.05 k g , K = 0.0001 , L = 0.01 H , R = 1 Ω , g = 9.81 m / s 2 , h = 0.01 m m=0.05kg,\;K=0.0001,\;L=0.01H,\;R=1Ω,\; g=9.81m/s^2,\;h=0.01m m = 0 . 0 5 k g , K = 0 . 0 0 0 1 , L = 0 . 0 1 H , R = 1 Ω , g = 9 . 8 1 m / s 2 , h = 0 . 0 1 m 식 F = m a F=ma F = m a h h h
{ m d 2 h d t 2 = m g − k i 2 h ⋯ ① V = L d i d t + R i ⋯ ② \begin{cases}m\frac{d^2h}{dt^2}=mg-\frac{ki^2}{h}\cdots①\\ V=L\frac{di}{dt}+Ri\;\;\;\;\,\cdots②\end{cases} { m d t 2 d 2 h = m g − h k i 2 ⋯ ① V = L d t d i + R i ⋯ ② 여기서 평형을 이루면 가속도가 없어지게 되므로 좌변이 0 0 0
0 = m g − k i 0 2 h 0 i 0 = m g h 0 k ≈ 7 A 0=mg-\frac{ki_0^2}{h_0}\\\,\\ i_0=\sqrt{\frac{mgh_0}{k}}\approx7A 0 = m g − h 0 k i 0 2 i 0 = k m g h 0 ≈ 7 A 평형점에서 L d i d t = 0 L\frac {di}{dt}=0 L d t d i = 0
L d i d t = 0 V 0 = R × i 0 = 1 × 7 = 7 V L\frac {di}{dt}=0\\\,\\ V_0=R\times i_0=1\times7=7V L d t d i = 0 V 0 = R × i 0 = 1 × 7 = 7 V 따라서 ①번 식은 다음과 같이 정리됩니다.
m d 2 d t 2 ( h 0 + Δ h ) = m g − k ( i 0 + Δ i ) 2 h 0 + Δ h m d 2 d t 2 ( Δ h ) = m g − k ( i 0 2 + 2 i 0 Δ i + Δ i 2 ) h 0 + Δ h ( ∵ d h 0 d t = 0 ) m d 2 d t 2 ( Δ h ) = m g − k ( i 0 2 + 2 i 0 Δ i ) h 0 + △ h ( ∵ Δ i 2 ≈ 0 ) m d 2 d t 2 ( Δ h ) = m g − k h 0 ( i 0 2 + 2 i 0 Δ i ) 1 + Δ h h 0 m\frac{d^2}{dt^2}(h_0+\Delta h)=mg-\frac{k(i_0+\Delta i)^2}{h_0+\Delta h}\\\,\\ m\frac{d^2}{dt^2}(\Delta h)=mg-\frac{k(i_0^2+2i_0\Delta i+\Delta i^2)}{h_0+\Delta h}(\because \frac{dh_0}{dt}=0)\\\,\\ m\frac{d^2}{dt^2}(\Delta h)=mg-\frac{k(i_0^2+2i_0\Delta i)}{h_0+\triangle h}(\because \Delta i^2\approx0)\\\,\\ m\frac{d^2}{dt^2}(\Delta h)=mg-\frac{\frac{k}{h_0}(i_0^2+2i_0\Delta i)}{1+\frac{\Delta h}{h_0}} m d t 2 d 2 ( h 0 + Δ h ) = m g − h 0 + Δ h k ( i 0 + Δ i ) 2 m d t 2 d 2 ( Δ h ) = m g − h 0 + Δ h k ( i 0 2 + 2 i 0 Δ i + Δ i 2 ) ( ∵ d t d h 0 = 0 ) m d t 2 d 2 ( Δ h ) = m g − h 0 + △ h k ( i 0 2 + 2 i 0 Δ i ) ( ∵ Δ i 2 ≈ 0 ) m d t 2 d 2 ( Δ h ) = m g − 1 + h 0 Δ h h 0 k ( i 0 2 + 2 i 0 Δ i )
무한등비급수의 테일러 전개: 1 1 − x = 1 + x + x 2 + x 3 + … , ( ∣ x ∣ < 1 ) \frac{1}{1-x}=1+x+x^2+x^3+\dots,(\vert x\vert<1) 1 − x 1 = 1 + x + x 2 + x 3 + … , ( ∣ x ∣ < 1 )
위의 마지막 식에서 x = △ h h 0 x=\frac{\triangle h}{h_0} x = h 0 △ h
m d 2 d t 2 ( Δ h ) = m g − k ( i 0 2 + 2 i 0 Δ i ) h 0 + k ( i 0 2 + 2 i 0 Δ i ) Δ h h 0 2 + … m d 2 d t 2 ( Δ h ) = m g − k ⋅ i 0 2 h 0 − 2 i 0 2 h 0 Δ i + k ( i 0 2 + 2 i 0 Δ i ) Δ h h 0 2 + … m d 2 d t 2 ( Δ h ) = − 2 i 0 2 h 0 Δ i + k ⋅ i 0 2 h 0 2 Δ h + k ⋅ 2 i 0 Δ i h 0 2 Δ h + … ( ∵ i n i t i a l c o n d i t i o n → 0 = m g − k i 0 2 h 0 ) m d 2 d t 2 ( Δ h ) = − 2 i 0 2 h 0 Δ i + k ⋅ i 0 2 h 0 2 Δ h + … ( ∵ Δ i × Δ h ≈ 0 ) m\frac{d^2}{dt^2}(\Delta h)=mg-\frac{k(i_0^2+2i_0\Delta i)}{h_0}+\frac{k(i_0^2+2i_0\Delta i)\Delta h}{h_0^2}+\dots\\\,\\ m\frac{d^2}{dt^2}(\Delta h)=mg-\frac{k\cdot i_0^2}{h_0}-\frac{2i_0^2}{h_0}\Delta i+\frac{k(i_0^2+2i_0\Delta i)\Delta h}{h_0^2}+\dots\\\,\\ m\frac{d^2}{dt^2}(\Delta h)=-\frac{2i_0^2}{h_0}\Delta i+\frac{k\cdot i_0^2}{h_0^2}\Delta h+\frac{k\cdot 2i_0\Delta i}{h_0^2}\Delta h+\dots\\ (\because initial\;condition\rarr 0=mg-\frac{ki_0^2}{h_0})\\\,\\ m\frac{d^2}{dt^2}(\Delta h)=-\frac{2i_0^2}{h_0}\Delta i+\frac{k\cdot i_0^2}{h_0^2}\Delta h+\dots\\ (\because \Delta i \times \Delta h \approx0)\\\,\\ m d t 2 d 2 ( Δ h ) = m g − h 0 k ( i 0 2 + 2 i 0 Δ i ) + h 0 2 k ( i 0 2 + 2 i 0 Δ i ) Δ h + … m d t 2 d 2 ( Δ h ) = m g − h 0 k ⋅ i 0 2 − h 0 2 i 0 2 Δ i + h 0 2 k ( i 0 2 + 2 i 0 Δ i ) Δ h + … m d t 2 d 2 ( Δ h ) = − h 0 2 i 0 2 Δ i + h 0 2 k ⋅ i 0 2 Δ h + h 0 2 k ⋅ 2 i 0 Δ i Δ h + … ( ∵ i n i t i a l c o n d i t i o n → 0 = m g − h 0 k i 0 2 ) m d t 2 d 2 ( Δ h ) = − h 0 2 i 0 2 Δ i + h 0 2 k ⋅ i 0 2 Δ h + … ( ∵ Δ i × Δ h ≈ 0 ) ②번식도 마찬가지로 정리할 수 있습니다.
L d d t ( i 0 + Δ i ) = − R ( i 0 + Δ i ) + V 0 + Δ V L d Δ i 0 d t = − R Δ i + Δ V ( ∵ − R i 0 + V 0 = 0 , d i 0 d t = 0 ) L\frac{d}{dt}(i_0+\Delta i)=-R(i_0+\Delta i)+V_0+\Delta V\\\,\\\ L\frac{d\Delta i_0}{dt}=-R\Delta i+\Delta V (\because -Ri_0+V_0=0,\;\frac{di_0}{dt}=0) L d t d ( i 0 + Δ i ) = − R ( i 0 + Δ i ) + V 0 + Δ V L d t d Δ i 0 = − R Δ i + Δ V ( ∵ − R i 0 + V 0 = 0 , d t d i 0 = 0 ) 두 식음 다음과 같이 정리되었습니다. 이 식으로 상태공간모델을 만듭니다.
{ d 2 Δ h d t 2 = − 2 i 0 2 m h 0 Δ i + k ⋅ i 0 2 m h 0 2 Δ h d Δ i 0 d t = − R Δ i L + Δ V L { x ˙ = ( 0 1 0 k i 0 2 m h 0 2 0 − 2 k i 0 m h 0 0 0 − R L ) ( Δ h Δ h ˙ Δ i ) + ( 0 0 1 L ) Δ V y = Δ h = ( 1 0 0 ) ( Δ h Δ h ˙ Δ i ) + ( 0 ) Δ V \begin{cases} \frac{d^2 \Delta h}{dt^2}=-\frac{2i_0^2}{mh_0}\Delta i+\frac{k\cdot i_0^2}{mh_0^2}\Delta h\\ \frac{d\Delta i_0}{dt}=-\frac{R\Delta i}{L}+\frac{\Delta V}{L} \end{cases}\\\,\\ \begin{cases} \dot x=\begin{pmatrix} 0 & 1 & 0 \\ \frac{ki_0^2}{mh_0^2} & 0 & -\frac{2ki_0}{mh_0} \\ 0 & 0 & -\frac RL \end{pmatrix}\begin{pmatrix}\Delta h\\\Delta\dot h\\\Delta i \end{pmatrix} + \begin{pmatrix}0\\0\\\frac 1L\end{pmatrix}\Delta V \\\,\\ y=\Delta h=\begin{pmatrix}1&0&0\end{pmatrix}\begin{pmatrix}\Delta h\\\Delta \dot h \\ \Delta i \end{pmatrix}+(0)\Delta V\end{cases} { d t 2 d 2 Δ h = − m h 0 2 i 0 2 Δ i + m h 0 2 k ⋅ i 0 2 Δ h d t d Δ i 0 = − L R Δ i + L Δ V ⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ x ˙ = ⎝ ⎜ ⎜ ⎛ 0 m h 0 2 k i 0 2 0 1 0 0 0 − m h 0 2 k i 0 − L R ⎠ ⎟ ⎟ ⎞ ⎝ ⎜ ⎛ Δ h Δ h ˙ Δ i ⎠ ⎟ ⎞ + ⎝ ⎜ ⎛ 0 0 L 1 ⎠ ⎟ ⎞ Δ V y = Δ h = ( 1 0 0 ) ⎝ ⎜ ⎛ Δ h Δ h ˙ Δ i ⎠ ⎟ ⎞ + ( 0 ) Δ V 위에서 구한 상태공간방정식에 L a p l a c e Laplace L a p l a c e Y u ( s ) \frac{Y}{u}(s) u Y ( s ) A A A Y u ( s ) \frac Yu(s) u Y ( s )