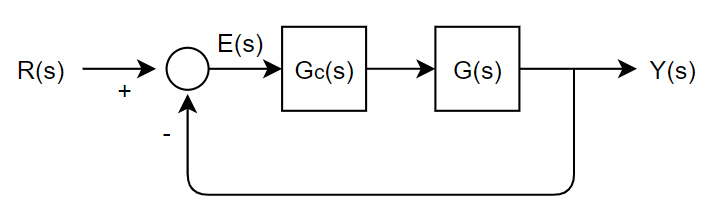
위와 같은 블럭선도가 있다고 할 때, 전달함수는 다음과 같습니다.

$Y(s)=(R(s)-Y(s))G_c(s)G(s)\\ (1+G_c(s)G(s))Y(s)=G_c(s)G(s)R(s)\\ Y=\frac{G_c(s)G(s)}{1+G_c(s)G(s)}R(s)\\\;\\ \frac{Y(s)}{R(s)}=G_c(s)G(s)=\frac{G_c(s)G(s)}{1+G_c(s)G(s)}$

오차의 정의는 다음과 같습니다.

$E(s)=R(s)-Y(s)=R(s)-\frac{G_c(s)G(s)}{1+G_c(s)G(s)}R(s)=\frac{1}{1+G_c(s)G(s)}R(s)$

Final value theorem에 따른 정상상태오차(steady state error)에 대한 정의는 다음과 같습니다.

$e_{ss}=\displaystyle\lim_{t\rarr\infin}e(t)=\displaystyle\lim_{s\rarr0}s\cdot E(s)$

Type

표준 시험 입력이 unit step $(R(s)=\frac 1s)$라고 한다면, 정상 상태 오차는 다음과 같습니다.

이때, $\displaystyle\lim_{s\rarr0}G_c(s)G(s)$의 형태에 따라서 정상 상태 오차가 결정됩니다.

여기서 $N$이 의미하는 바는 (분자의 $s$의 최고차수 - 분모의 $s$의 최고차수)입니다.
$N$이 1보다 크다면 $\displaystyle\lim_{s\rarr0}G_c(s)G(s)$는 무한대로 발산하게 되고, $e_{ss}$는 0으로 수렴하게 됩니다.
$N$에 따라서 입력에 따른 정상상태오차의 형태가 달라지게 됩니다.
그래서 $N$에 따라 전달함수의 타입을 구분하여 $type\;N$이라고 합니다.

여기서의 상수 $G_c(0)G(0)$, 즉 $\displaystyle\lim_{s\rarr0}G_c(s)G(s)$를 위치오차상수 $K_p$라고 합니다.