주파수 영역의 제어 시스템
오늘 우리의 목표는 type2 제어 시스템에서 M p , t s , t r M_p, t_s, t_r M p , t s , t r 0 ≤ ζ < 1 0 \leq \zeta < 1 0 ≤ ζ < 1 G ( s ) G(s) G ( s )
G ( s ) = Y ( s ) R ( s ) = ω n 2 s 2 + 2 ζ ω n s + ω n 2 G(s)=\frac{Y(s)}{R(s)}=\frac{\omega_n^2}{s^2+2\zeta\omega_n s+\omega_n^2} G ( s ) = R ( s ) Y ( s ) = s 2 + 2 ζ ω n s + ω n 2 ω n 2
여기서 R ( s ) R(s) R ( s ) 1 s \frac1s s 1
Y ( s ) = ω n 2 s 2 + 2 ζ ω n s + ω n 2 1 s Y(s)=\frac{\omega_n^2}{s^2+2\zeta\omega_n s+\omega_n^2}\frac1s Y ( s ) = s 2 + 2 ζ ω n s + ω n 2 ω n 2 s 1 부분분수 분리
헤비사이드 부분 분수 분리법을 이용하면 1 s \frac1s s 1
Y ( s ) = ( ω n 2 s 2 + 2 ζ ω n s + ω n 2 1 s ) × s = ( A s + B s + C s 2 + 2 ζ ω n s + ω n 2 ) ) × s Y(s)=(\frac{\omega_n^2}{s^2+2\zeta\omega_n s+\omega_n^2}\frac1s)\times s = (\frac As+\frac{Bs+C}{s^2+2\zeta\omega_n s+\omega_n^2)})\times s Y ( s ) = ( s 2 + 2 ζ ω n s + ω n 2 ω n 2 s 1 ) × s = ( s A + s 2 + 2 ζ ω n s + ω n 2 ) B s + C ) × s
여기서 s = 0 s = 0 s = 0
ω n 2 ω n 2 = A \frac{\omega_n^2}{\omega_n^2}=A ω n 2 ω n 2 = A A = 1 A = 1 A = 1
Y ( s ) = 1 s + B s + C s 2 + 2 ζ ω n s + ω n 2 Y(s)=\frac 1s+\frac{Bs+C}{s^2+2\zeta\omega_n s+\omega_n^2} Y ( s ) = s 1 + s 2 + 2 ζ ω n s + ω n 2 B s + C
나머지 B , C B, C B , C
ω n 2 s 2 + 2 ζ ω n s + ω n 2 × 1 s = B s 2 + C s + s 2 + 2 ζ ω n s + ω n 2 s 2 + 2 ζ ω n s + ω n 2 × 1 s \frac{\omega_n^2}{s^2+2\zeta\omega_n s+\omega_n^2 }\times \frac1s = \frac{Bs^2+Cs+s^2+2\zeta\omega_n s+\omega_n^2}{s^2+2\zeta\omega_n s+\omega_n^2}\times \frac1s s 2 + 2 ζ ω n s + ω n 2 ω n 2 × s 1 = s 2 + 2 ζ ω n s + ω n 2 B s 2 + C s + s 2 + 2 ζ ω n s + ω n 2 × s 1
{ B s 2 + s 2 = 0 ⇒ B = − 1 C s + 2 ζ ω n s = 0 ⇒ C = − 2 ζ ω n \begin{cases} Bs^2+s^2=0 \Rightarrow B = -1\\ Cs + 2\zeta\omega_ns = 0 \Rightarrow C=-2\zeta\omega_n \end{cases} { B s 2 + s 2 = 0 ⇒ B = − 1 C s + 2 ζ ω n s = 0 ⇒ C = − 2 ζ ω n
Y ( s ) = 1 s − s + 2 ζ ω n s 2 + 2 ζ ω n s + ω n 2 Y(s)=\frac 1s-\frac{s+2\zeta\omega_n}{s^2+2\zeta\omega_n s+\omega_n^2} Y ( s ) = s 1 − s 2 + 2 ζ ω n s + ω n 2 s + 2 ζ ω n 라플라스 역변환
복잡한 두 번째 항을 다음 세 가지 라플라스 역변환 공식을 이용하여 정리합니다.
{ 1. e a t = L − 1 { 1 s − a } 2. sin ( a t ) = L − 1 { a s 2 − a 2 } 3. cos ( a t ) = L − 1 { s s 2 − a 2 } \begin{cases} 1. e^{at}=\mathcal{L}^{-1}\{{\frac1{s-a}}\}\\ 2. \sin(at)=\mathcal{L}^{-1}\{{\frac a{s^2-a^2}}\}\\ 3. \cos(at)=\mathcal{L}^{-1}\{{\frac s{s^2-a^2}}\}\\ \end{cases} ⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ 1 . e a t = L − 1 { s − a 1 } 2 . sin ( a t ) = L − 1 { s 2 − a 2 a } 3 . cos ( a t ) = L − 1 { s 2 − a 2 s } Y ( s ) = 1 s − s + 2 ζ ω n ( s + ζ ω n ) 2 − ζ 2 ω n 2 + ω n 2 Y(s)=\frac 1s-\frac{s+2\zeta\omega_n}{(s+\zeta\omega_n)^2-\zeta^2\omega_n^2 + \omega_n^2} Y ( s ) = s 1 − ( s + ζ ω n ) 2 − ζ 2 ω n 2 + ω n 2 s + 2 ζ ω n
Y ( s ) = 1 s − s + 2 ζ ω n ( s + ζ ω n ) 2 + ω n 2 ( 1 − ζ 2 ) Y(s)=\frac 1s-\frac{s+2\zeta\omega_n}{(s+\zeta\omega_n)^2+\omega_n^2(1-\zeta^2)} Y ( s ) = s 1 − ( s + ζ ω n ) 2 + ω n 2 ( 1 − ζ 2 ) s + 2 ζ ω n
Y ( s ) = 1 s − s + 2 ζ ω n ( s + ζ ω n ) 2 + ω d 2 ( ∵ ω d = 1 − ζ 2 ) Y(s)=\frac 1s-\frac{s+2\zeta\omega_n}{(s+\zeta\omega_n)^2+\omega_d^2}(\because \omega_d=\sqrt{1-\zeta^2}) Y ( s ) = s 1 − ( s + ζ ω n ) 2 + ω d 2 s + 2 ζ ω n ( ∵ ω d = 1 − ζ 2 )
Y ( s ) = 1 s − s + ζ ω n ( s + ζ ω n ) 2 + ω d 2 + ζ ω n ( s + ζ ω n ) 2 + ω d 2 Y(s)=\frac 1s-\frac{s+\zeta\omega_n}{(s+\zeta\omega_n)^2+\omega_d^2}+\frac{\zeta\omega_n}{(s+\zeta\omega_n)^2+\omega_d^2} Y ( s ) = s 1 − ( s + ζ ω n ) 2 + ω d 2 s + ζ ω n + ( s + ζ ω n ) 2 + ω d 2 ζ ω n
L − 1 Y ( s ) = L − 1 { 1 s − s + ζ ω n ( s + ζ ω n ) 2 + ω d 2 + ζ ω n ( s + ζ ω n ) 2 + ω d 2 } \mathcal{L}^{-1}{Y(s)}=\mathcal{L}^{-1}\{\frac 1s-\frac{s+\zeta\omega_n}{(s+\zeta\omega_n)^2+\omega_d^2}+\frac{\zeta\omega_n}{(s+\zeta\omega_n)^2+\omega_d^2}\} L − 1 Y ( s ) = L − 1 { s 1 − ( s + ζ ω n ) 2 + ω d 2 s + ζ ω n + ( s + ζ ω n ) 2 + ω d 2 ζ ω n }
y ( t ) = L − 1 { 1 s } − L − 1 { s + ζ ω n ( s + ζ ω n ) 2 + ω d 2 } + L − 1 { ζ ω n ( s + ζ ω n ) 2 + ω d 2 } y(t)=\mathcal{L}^{-1}\left\{\frac 1s\right\}-\mathcal{L}^{-1}\left\{\frac{s+\zeta\omega_n}{(s+\zeta\omega_n)^2+\omega_d^2}\right\}+\mathcal{L}^{-1}\left\{\frac{\zeta\omega_n}{(s+\zeta\omega_n)^2+\omega_d^2}\right\} y ( t ) = L − 1 { s 1 } − L − 1 { ( s + ζ ω n ) 2 + ω d 2 s + ζ ω n } + L − 1 { ( s + ζ ω n ) 2 + ω d 2 ζ ω n } 1번 공식을 적용하여 ζ ω n \zeta\omega_n ζ ω n
y ( t ) = 1 − e − ζ ω n t L − 1 { s s 2 + ω d 2 } + e − ζ ω n t L − 1 { ζ ω n s 2 + ω d 2 } y(t)=1-e^{-\zeta\omega_nt}\mathcal{L}^{-1}\{\frac{s}{s^2+\omega_d^2}\}+e^{-\zeta\omega_nt}\mathcal{L}^{-1}\{\frac{\zeta\omega_n}{s^2+\omega_d^2}\} y ( t ) = 1 − e − ζ ω n t L − 1 { s 2 + ω d 2 s } + e − ζ ω n t L − 1 { s 2 + ω d 2 ζ ω n }
이제 2번 공식을 이용하여 두번째 항을 변환하면 다음과 같습니다.
y ( t ) = 1 − e − ζ ω n t ( cos ( ω d t ) + L − 1 { ζ ω n s 2 + ω d 2 } ) y(t) = 1-e^{-\zeta\omega_nt}(\cos(\omega_dt)+\mathcal{L}^{-1}\{\frac{\zeta\omega_n}{s^2+\omega_d^2}\}) y ( t ) = 1 − e − ζ ω n t ( cos ( ω d t ) + L − 1 { s 2 + ω d 2 ζ ω n } )
세 번째 항은 바로 변환할 수 없기 때문에 조금 변형이 필요하다.
ω d = ω n 1 − ζ 2 \omega_d=\omega_n\sqrt{1-\zeta^2} ω d = ω n 1 − ζ 2 ω n \omega_n ω n ω d \omega_d ω d
y ( t ) = 1 − e − ζ ω n t ( cos ( ω d t ) + L − 1 { ζ s 2 + ω d 2 ω d 1 − ζ 2 } ) y(t) = 1-e^{-\zeta\omega_nt}(\cos(\omega_dt)+\mathcal{L}^{-1}\{\frac{\zeta}{s^2+\omega_d^2}\frac{\omega_d}{\sqrt{1-\zeta^2}}\}) y ( t ) = 1 − e − ζ ω n t ( cos ( ω d t ) + L − 1 { s 2 + ω d 2 ζ 1 − ζ 2 ω d } )
y ( t ) = 1 − e − ζ ω n t ( cos ( ω d t ) + ζ 1 − ζ 2 L − 1 { ω d s 2 + ω d 2 } ) y(t) = 1-e^{-\zeta\omega_nt}(\cos(\omega_dt)+\frac{\zeta}{\sqrt{1-\zeta^2}}\mathcal{L}^{-1}\{\frac{\omega_d}{s^2+\omega_d^2}\}) y ( t ) = 1 − e − ζ ω n t ( cos ( ω d t ) + 1 − ζ 2 ζ L − 1 { s 2 + ω d 2 ω d } )
y ( t ) = 1 − e − ζ ω n t ( cos ( ω d t ) + ζ 1 − ζ 2 sin ( ω d t ) ) y(t) = 1-e^{-\zeta\omega_nt}(\cos(\omega_dt)+\frac{\zeta}{\sqrt{1-\zeta^2}}\sin(\omega_dt)) y ( t ) = 1 − e − ζ ω n t ( cos ( ω d t ) + 1 − ζ 2 ζ sin ( ω d t ) ) 여기서 삼각함수의 합성 공식을 이용하여 더 정리가 가능합니다.a sin ( x ) + b cos ( x ) = a 2 + b 2 sin ( x + α ) a \sin(x) + b \cos(x)=\sqrt{a^2+b^2} \sin(x+\alpha) a sin ( x ) + b cos ( x ) = a 2 + b 2 sin ( x + α ) α \alpha α
y ( t ) = 1 − e − ζ ω n t 1 − ζ 2 sin ( ω d t + ϕ ) y(t)=1-\frac{e^{-\zeta\omega_nt}}{\sqrt{1-\zeta^2}} \sin(\omega_dt+\phi) y ( t ) = 1 − 1 − ζ 2 e − ζ ω n t sin ( ω d t + ϕ ) 그래프
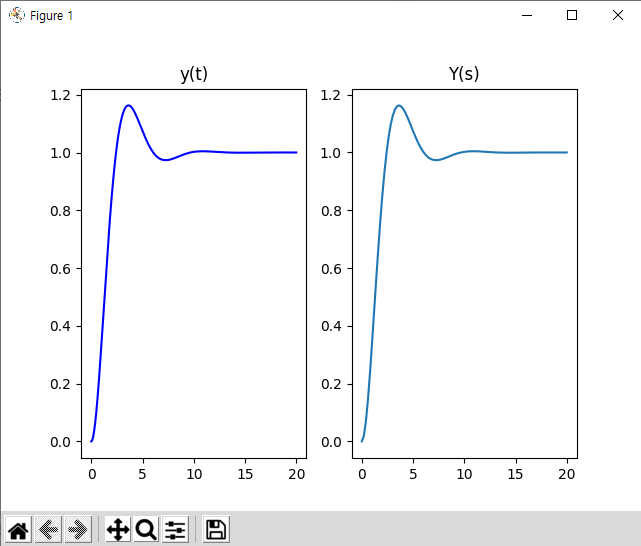
라플라스 역변환을 통하여 도출된 식이 올바르게 도출되었는지 그래프를 출력하여 검증하여 보겠습니다.y ( t ) y(t) y ( t ) Y ( s ) Y(s) Y ( s ) ζ = 0.5 \zeta=0.5 ζ = 0 . 5 ω n = 1 \omega_n=1 ω n = 1
import matplotlib. pyplot as plt
import numpy as np
import control. matlab as ctrl
zeta = 0.5
omega_n = 1
omega_d = omega_n* np. sqrt( 1 - zeta** 2 )
t = np. arange( 0 , 10 , 0.01 )
yt = 1 - np. exp( - zeta* omega_n* t) * ( np. cos( omega_d* t) + zeta/ np. sqrt( 1 - zeta** 2 ) * np. sin( omega_d* t) )
plt. subplot( 1 , 2 , 1 )
plt. title( 'y(t)' )
plt. plot( t, yt, 'b-' )
num = np. array( [ omega_n** 2 ] )
den = np. array( [ 1 , 2 * zeta, omega_n** 2 ] )
sys = ctrl. tf( num, den)
y, t = ctrl. step( sys, T= 10 )
plt. subplot( 1 , 2 , 2 )
plt. title( 'Y(s)' )
plt. plot( t, y)
plt. show( ) ζ , ω \zeta, \omega ζ , ω
Envelope
제어 시스템은 요동치며 수렴하게 됩니다. 왜 그럴까요?sin \sin sin
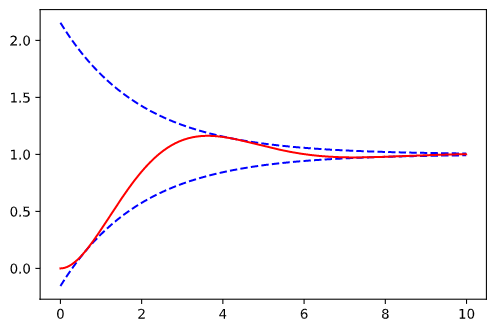
y ( t ) = 1 − e − ζ ω n t 1 − ζ 2 sin ( ω d t + ϕ ) y(t)=1-\frac{e^{-\zeta\omega_nt}}{\sqrt{1-\zeta^2}} \sin(\omega_dt+\phi) y ( t ) = 1 − 1 − ζ 2 e − ζ ω n t sin ( ω d t + ϕ ) 그래서 이 시스템을 위 아래로 자연스러운 곡선으로 연결하는 함수는 다음과 같습니다.
f ( t ) = 1 ± e − ζ ω n t 1 − ζ 2 f(t)=1±\frac{e^{-\zeta\omega_nt}}{\sqrt{1-\zeta^2}} f ( t ) = 1 ± 1 − ζ 2 e − ζ ω n t 실제로 그런지 출력을 해보겠습니다.
import matplotlib. pyplot as plt
import numpy as np
zeta = 0.5
omega_n = 1
omega_d = omega_n* np. sqrt( 1 - zeta** 2 )
t = np. arange( 0 , 10 , 0.01 )
yt = 1 - np. exp( - zeta* omega_n* t) * ( np. cos( omega_d* t) + zeta/ np. sqrt( 1 - zeta** 2 ) * np. sin( omega_d* t) )
envelope1 = 1 - np. exp( - zeta* omega_n* t) / np. sqrt( 1 - zeta** 2 )
envelope2 = 1 + np. exp( - zeta* omega_n* t) / np. sqrt( 1 - zeta** 2 )
plt. plot( t, envelope1, 'b--' )
plt. plot( t, envelope2, 'b--' )
plt. plot( t, yt, 'r-' )
plt. show( )
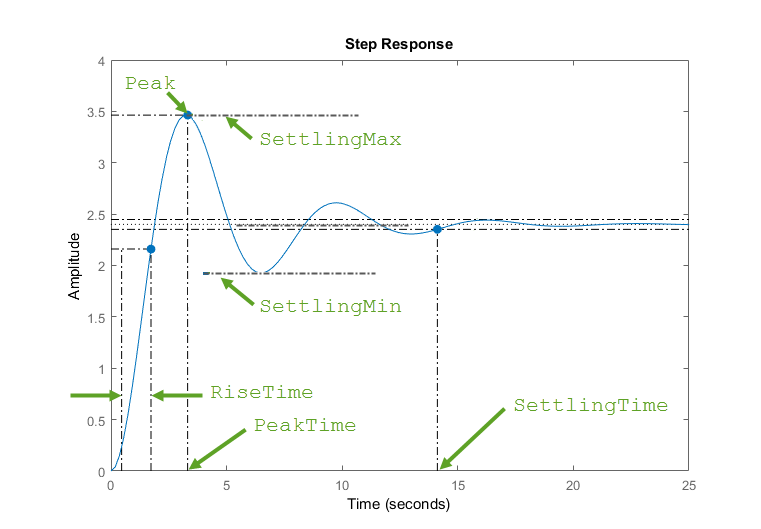
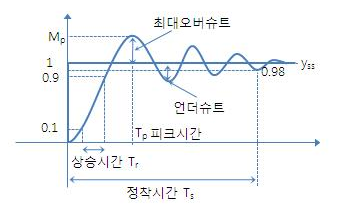
시스템의 해석
이러한 응답 그래프에서 얻을 수 있는 정보는 다음과 같습니다.
t p : t_p: t p : y ( t ) y(t) y ( t ) y ˙ ( t p ) = 0 \dot y(t_p)=0 y ˙ ( t p ) = 0 t p t_p t p
y ˙ ( t ) = e ζ ω n t p sin ( ω d t p ) ( − ζ ω n ( ζ ω n ω d ) + ( − ω d ) ) = 0 \dot y(t)=e^{\zeta \omega_n t_p}\sin(\omega_d t_p)(-\zeta\omega_n(\frac{\zeta\omega_n}{\omega_d})+(-\omega_d))=0 y ˙ ( t ) = e ζ ω n t p sin ( ω d t p ) ( − ζ ω n ( ω d ζ ω n ) + ( − ω d ) ) = 0
sin ( ω d t p ) = 0 \sin(\omega_d t_p)=0 sin ( ω d t p ) = 0
ω d t p = 0 , π , 2 π , 3 π , . . . \omega_d t_p = 0, \pi, 2\pi, 3\pi, ... ω d t p = 0 , π , 2 π , 3 π , . . .
0은 의미가 없으므로 ω d t p = π \omega_d t_p = \pi ω d t p = π
t p = π ω d t_p = \frac{\pi}{\omega_d} t p = ω d π M p : M_p: M p : M p M_p M p y ( t ) y(t) y ( t ) y ( t p ) y(t_p) y ( t p ) M p = y ( t p ) − 1 = y ( π ω d ) − 1 = 1 − e − ζ ω n ( π ω d ) ( cos ( ω d ( π ω d ) ) + ζ 1 − ζ 2 sin ( ω d ( π ω d ) ) ) − 1 = e − ζ π 1 − ζ 2 ( ∵ ω d = ω n 1 − ζ 2 ) \begin{aligned} M_p &= y(t_p)-1\\ &=y(\frac{\pi}{\omega_d})-1\\ &=1-e^{-\zeta\omega_n(\frac{\pi}{\omega_d})}(\cos(\omega_d(\frac{\pi}{\omega_d}))+\frac{\zeta}{\sqrt{1-\zeta^2}}\sin(\omega_d(\frac{\pi}{\omega_d})))-1\\ &=e^{\frac{-\zeta\pi}{\sqrt{1-\zeta^2}}} (\because \omega_d=\omega_n\sqrt{1-\zeta^2}) \end{aligned} M p = y ( t p ) − 1 = y ( ω d π ) − 1 = 1 − e − ζ ω n ( ω d π ) ( cos ( ω d ( ω d π ) ) + 1 − ζ 2 ζ sin ( ω d ( ω d π ) ) ) − 1 = e 1 − ζ 2 − ζ π ( ∵ ω d = ω n 1 − ζ 2 )
M p = e − ζ π 1 − ζ 2 M_p =e^{\frac{-\zeta\pi}{\sqrt{1-\zeta^2}}} M p = e 1 − ζ 2 − ζ π 따라서 M p M_p M p ζ \zeta ζ
P O : PO: P O : overshoot을 퍼센트 비율로 나타낸 것입니다.
P O = y ( t p ) − y ( ∞ ) y ( ∞ ) × 100 % = y ( t p ) − 1 1 × 100 % = ( 1 − e − ζ ω n ( π ω d ) ( cos ( ω d ( π ω d ) ) + ζ 1 − ζ 2 sin ( ω d ( π ω d ) ) ) − 1 ) × 100 % = 100 e − ζ π 1 − ζ 2 % \begin{aligned} PO&=\frac{y(t_p)-y(\infin)}{y(\infin)}\times100\%\\ &=\frac{y(t_p)-1}{1}\times100\%\\ &=(1-e^{-\zeta\omega_n(\frac{\pi}{\omega_d})}(\cos(\omega_d(\frac{\pi}{\omega_d}))+\frac{\zeta}{\sqrt{1-\zeta^2}}\sin(\omega_d(\frac{\pi}{\omega_d})))-1)\times100\%\\ &=100e^{\frac{-\zeta\pi}{\sqrt{1-\zeta^2}}}\% \end{aligned} P O = y ( ∞ ) y ( t p ) − y ( ∞ ) × 1 0 0 % = 1 y ( t p ) − 1 × 1 0 0 % = ( 1 − e − ζ ω n ( ω d π ) ( cos ( ω d ( ω d π ) ) + 1 − ζ 2 ζ sin ( ω d ( ω d π ) ) ) − 1 ) × 1 0 0 % = 1 0 0 e 1 − ζ 2 − ζ π %
P O = 100 e − ζ π 1 − ζ 2 % PO=100e^{\frac{-\zeta\pi}{\sqrt{1-\zeta^2}}}\% P O = 1 0 0 e 1 − ζ 2 − ζ π % t s : t_s: t s : 사실 우리의 응답곡선은 무한한 시간이 지나도 결코 1이 될 순 없습니다.t s t_s t s t s t_s t s e − ζ ω n t 1 − ζ 2 < 0.02 \frac{e^{-\zeta\omega_nt}}{\sqrt{1-\zeta^2}}<0.02 1 − ζ 2 e − ζ ω n t < 0 . 0 2 t t t
t s ≊ 4 ζ ω n f o r 2 % c r i t e r i o n t_s\approxeq\frac{4}{\zeta\omega_n}\quad for\;2\%\;criterion t s ≊ ζ ω n 4 f o r 2 % c r i t e r i o n t s ≊ 3 ζ ω n f o r 5 % c r i t e r i o n t_s\approxeq\frac{3}{\zeta\omega_n}\quad for\;5\%\;criterion t s ≊ ζ ω n 3 f o r 5 % c r i t e r i o n 

수식 깔끔하다 뭘로쓴거?