[ DFL ] distribution focal loss

d4r6j·2024년 7월 3일

vision-paper

목록 보기

9/11

Focal Loss

Focal Loss 는

training 중에 foreground 와 background 사이의 극도의 불균형이 있는 one-stage 객체 탐지 시나리오를 해결하기 위해 설계되었다.
binary classification 을 위한 cross entropy 로부터 시작하는 focal loss 를 소개한다.

{\rm CE}(p, y) = \begin{aligned} &\begin{cases} -\log(p) & {\rm if} \; y=1 \\ -\log(1-p) & {\rm otherwise.} \end{cases} \end{aligned}

위에서 $y \in \{ \pm 1\}$ 은 ground-truth class 로 정하고, $p \in [0, 1]$ 은 label $y=1$ class 에 대한 모델의 추정 확률 이다. notational 의 편의를 위해서 $p_t$ 로 정의한다.

p_t = \begin{aligned} &\begin{cases} p & {\rm if} \; y=1 \\ 1-p & {\rm otherwise.} \end{cases} \end{aligned}

${\rm CE}(p, y) = {\rm CE}(p_t) = -\log(p_t)$

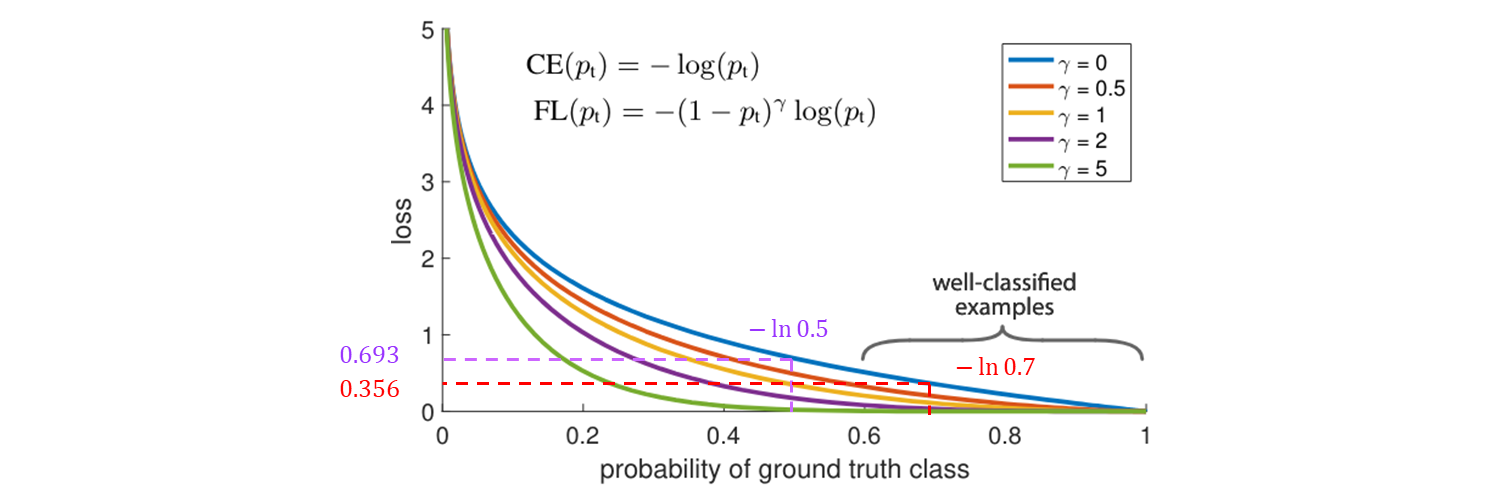
Cross Entropy loss 는 blue curve 이다.
이 plot 에서 보다시피 이 loss 의 주목 할 만한 속성 중 하나는 쉽게 분류되는 예제 $(p_t \gg 0.5)$ 일지라도 적지 않은 규모의 loss 가 일어난다는 것.
많은 수의 쉬운 예시 들을 더할 때, 이 많은 small loss 값들이 rare class 를 압도할 수 있다.

Balanced Cross Entropy

class 불균형 문제를 해결하기 위한 보통의 방법은
- class '1' 에는 weighting factor $\alpha \in [0, 1]$ 와 class '-1' 에 $(1-\alpha)$ 을 도입 하는 것.
- 실제 $\alpha$ 는 inverse class 빈도로 설정 되거나 cross validation 에 의해 설정되는 hyperparameter 로 처리 될 수 있다.
notational 편의를 위해서 $p_t$ 를 정의한 방법과 유사하게 $\alpha_t$ 를 정의한다.
$\alpha$ -balanced ${\rm CE}$ loss 를 아래와 같이 쓴다.
${\rm CE}(p_t) = -\alpha_t \log (p_t)$
이 loss 는 focal loss 를 위한 experimental baseline 으로 하는 ${\rm CE}$ 의 간단한 확장 loss 이다.

Focal Loss Definition

dense detector 는 이미지의 모든 위치에서 객체를 예측하려고 시도하는 object detect model 이다.
dense detector 의 훈련 중에 발생하는 많은 클래스들 의 불균형은 ${\rm CE}$ loss 를 압도할 수 있다.
- 쉽게 분류된 negative 들은 loss 의 대부분을 구성하고 gradient 를 지배한다.
$\alpha$ 는
- positive 와 negative 예시들의 중요성의 균형을 잡지만,
- easy 예시 와 hard 예시들 사이에서는 구별 하지 않는다.
대신에 loss function 을 reshape (재구성) 하여 easy 예시들은 down-weight 하고 hard negatives 에 초점을 맞춰 training 한다.

조정 가능한, focusing parameter $\gamma \geq 0$ 를 사용하여 ${\rm CE}$ loss 에 변조 factor $(1-p_t)^{\gamma}$ 를 추가한다.

{\rm FL}(p_t) = -(1-p_t)^{\gamma}\log(p_t)

def forward(pred, label, gamma=1.5, alpha=0.25):

    loss = F.binary_cross_entropy_with_logits(pred, label, reduction="none")
    pred_prob = pred.sigmoid()  # prob from logits
    p_t = label * pred_prob + (1 - label) * (1 - pred_prob)
    
    modulating_factor = (1.0 - p_t) ** gamma
    loss *= modulating_factor
    
    if alpha > 0:
        alpha_factor = label * alpha + (1 - label) * (1 - alpha)
        loss *= alpha_factor
        
    return loss.mean(1).sum()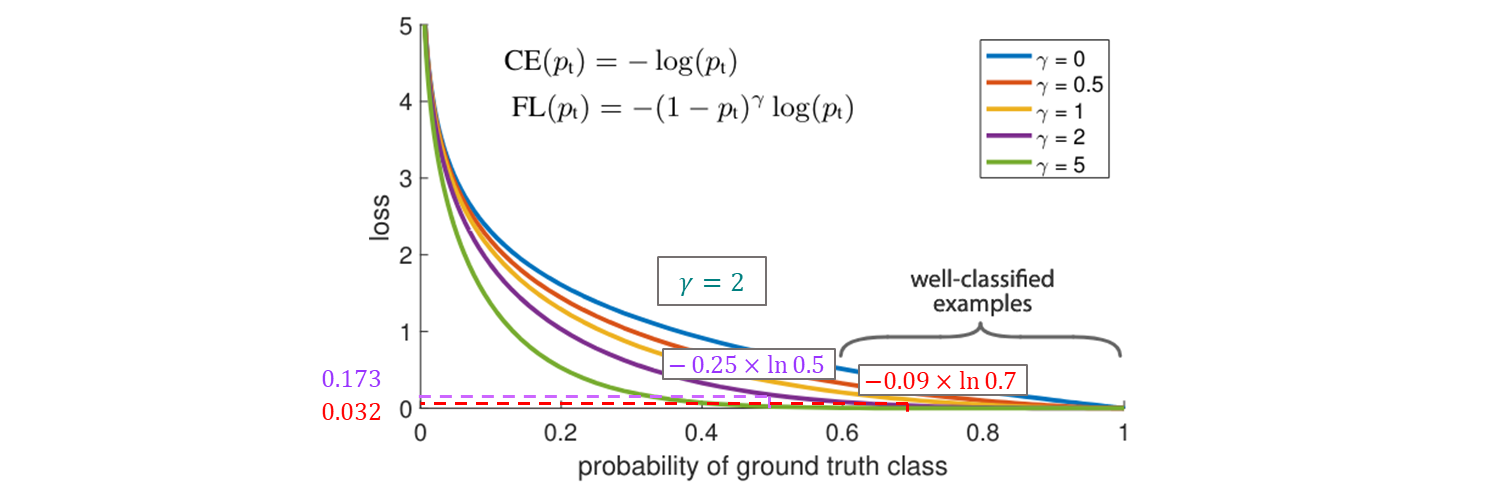

focal loss 는 $\gamma \in [0, 5]$ 의 몇 가지 값 들로 visualized 했다.
기존 ${\rm CE}$ 와 $\gamma = 2$ 를 비교할 경우
- $p(0.5) : 0.693 \rightarrow 0.173, \quad p(0.7) : 0.356 \rightarrow 0.032$

그래프보다 수치로 봐야 감이 훨씬 잘 온다.

focal loss 의 두 가지 속성들에 주목한다.

예시가 오분류 되고 $p_t$ 가 작을 때,
- 변조 factor 는 1에 가깝고 $(p_t \rightarrow 0)$ loss 는 영향을 적게 받는다.
- $p_t \rightarrow 1$ 로 가면 factor 는 0 이고 well-classified 예시들에 대한 loss 는 down-weighted 된다.
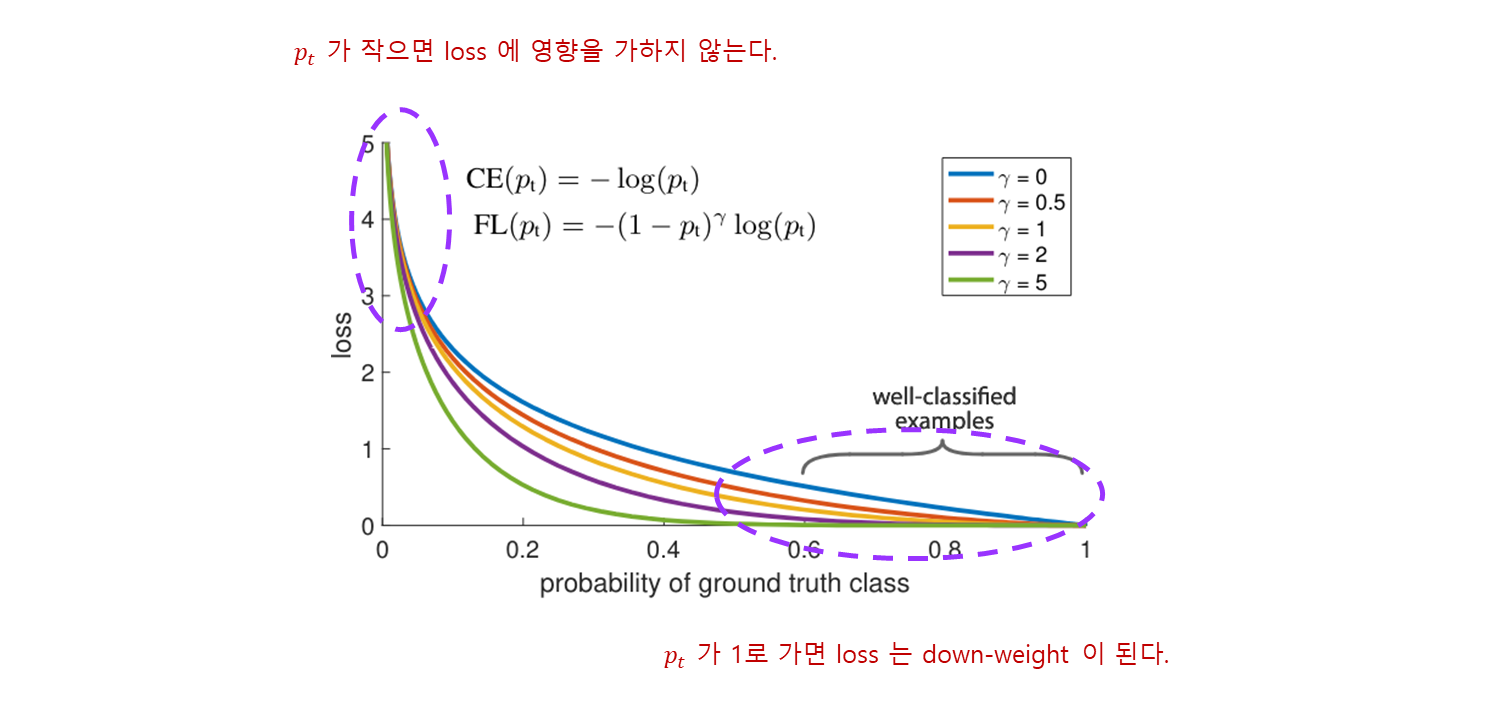
focusing parameter 인 $\gamma$ 는 쉬운 예제들의 비율을 down-weighted 속도를 부드럽게 조절한다.
- loss 를 거의 주지 않아서, small loss 들이 모여서 rare class 를 넘어가지 못하게 만든다.
- $\gamma = 0$ 일 때, Focal Loss 는 Cross Entropy 이고, $\gamma$ 가 증가할수록 modulation factor 의 효과도 비슷하게 증가된다. ( $\gamma = 2$ 에서 가장 좋게 동작하였다. )

modulating factor 는 쉬운 예제들로부터 loss 기여도를 줄이고, example 들에 대한 낮은 손실 범위를 확장 시킨다.
예를 들어 Cross Entropy 에서 받는 loss 와 비교했을 때 $\gamma = 2$ 일 경우,
- $p_t = 0.9$ 에서 분류된 example 은 100 배 작다.
- $p_t \approx 0.968$ 에서 분류된 example 은 1000 배 작다.
이것은 오분류된 examples 를 올바르게 하는 것의 중요성을 증가 시킨다.
- $p_t \leq .5, \gamma = 2$ 일 때 loss 가 최대로 4배 축소된다.
실제로 focal loss 의 $\alpha$ -balanced 변형을 사용한다.
${\rm FL}(p_t) = -\alpha_t(1-p_t)^{\gamma}\log(p_t)$
non- $\alpha$ -balance form 에 비해 정확도가 약간 향상되어서 채택하였다.

마지막으로, loss layer 의 개발은 $p$ 를 계산하기 위한 sigmoid 연산과 loss 계산의 결합으로 수치적 안정성을 높이는 것이 포인트다.

Class Imbalance and Model Initialization

Binary classification 모델들은 $y = -1$ 또는 $1$ 중 하나를 출력 확률이 같도록 default 초기화를 한다.
이와 같은 초기화에서, class 불균형이 나타나는 경우, 잦은 class 로 인한 loss 로 인하여 total loss 가 치솟을 수 있고, early training 에서 불안정성이 초래할 수 있다.
이것에 대처하기 위해서, training 이 시작할 때, rare class 를 위한 model 에 의해 추정된 $p$ 의 값에 대한 prior 의 개념을 도입한다.
$\pi$ 에 의해 prior 를 나타내고, rare class 의 예시들에 대해 모델의 추정된 $p$ 가 low 하도록 $(0.01)$ 설정한다. 이는 loss function 이 아니고, 모델 초기화의 변경이다.
이런 방법은 heavy 한 클래스 불균형의 case 에서 cross entropy 와 focal loss 사이에서 훈련의 안정성을 향상시키는 것으로 나타났다.

Generalized Focal Loss

우선 one-stage detectors 의 dense classification scores 를 학습하기 위한 Focal Loss 를 review 한다.
다음, 제안된 Quality Focal Loss $({\rm QFL})$ 과 Distribution Focal Loss $({\rm DFL})$ 을 통해 성공적으로 최적화된 localization quality 추정 과 bounding box 의 향상된 표현에 대한 detail 한 정보 나타낸다.
마지막으로 ${\rm FL}$ 의 유연한 확장으로써 ${\rm QFL}$ 과 ${\rm DFL}$ 을 Generalized Focal Loss $({\rm GFL})$ 통일된 관점으로 공식화하여 향후에 추가적인 프로모션과 일반적인 이해를 하기위해 가능하게 한다.

Focal Loss (FL)

${\rm FL}$ 은 훈련하는 동안, foreground 와 background 클래스들 사이에 극단적인 불균형이 존재하는 one-stage object detection 시나리오를 해결하기 위해 제안되었다. ${\rm FL}$ 은 아래를 따른다.

{\rm FL}(p) = - (1-p_t)^{\gamma}\log(p_t), \; p_t= \begin{aligned} &\begin{cases} p & {\rm when} \; y=1 \\ 1-p & {\rm when} \; y=0 \end{cases} \end{aligned}

여기서 $y \in \{1, 0\}$ ground-truth 클래스로 명시하고, $p \in [0, 1]$ 은 label $y=1$ 클래스를 위한 추정 확률이고, $\gamma$ 는 조정할 수 있는 focusing parameter 이다.
${\rm FL}$ 은 ${\rm CE}$ 의 $- \log(p_t)$ 부분과 동적 scaling factor 부분의 $\left( 1-p_t \right)^\gamma$ 으로 구성된다.
여기서 scaling factor $\left( 1-p_t \right)^\gamma$ 는 자동적으로 훈련하는 동안 쉬운 예제들의 기여를 down-weights 하고, 어려운 예제들을 모델에 빠르게 집중시킨다.

Quality Focal Loss (QFL)

training 과 test 단계 사이에서 앞서 언급한 불일치 문제를 해결하기 위해서
1. localization quality ( i.e. IoU score )
2. classification score ( ”classification-IoU” for short )
를 같이 표현하는 것을 제안한다.
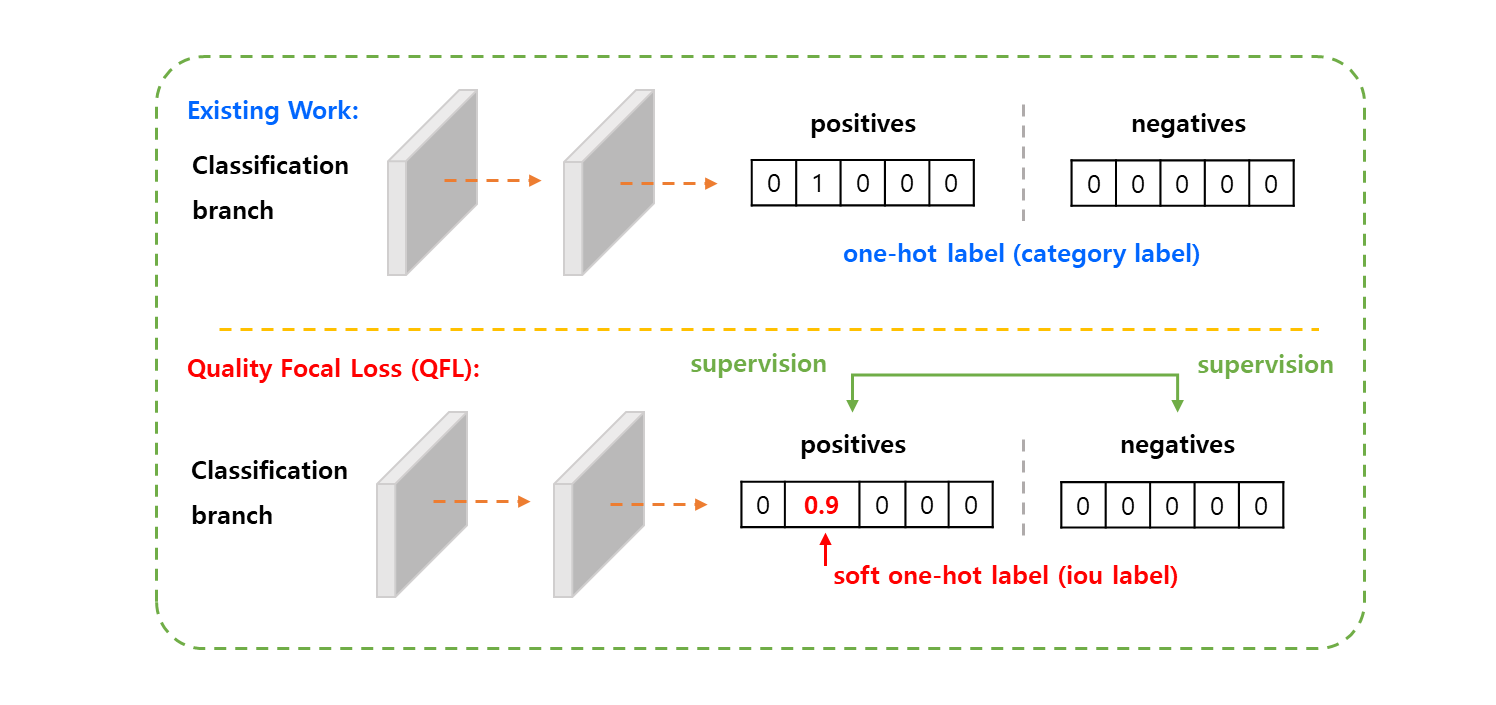
여기서 supervision 은 표준 one-hot 분류 label 을 부드럽게 하고, 일치하는 category 에 대해서 가능한 float target $y \in [0, 1]$ 으로 연결된다.

구체적으로 $y=0$ 은 quality score 가 $0$ 인 negative sample 들로 나타내고, $0 < y \leq 1$ 은 target IoU score $y$ 가 있는 positive sample 들을 의미한다.
localization quality label $y$ 는 전통적인 정의를 따르고, 학습 중 예측된 bounding box 와 ground-truth bounding box 사이에서 IoU score 동적 value 는 $0 \sim 1$ 이다.
multi-class 구현 을 위해 sigmoid 연산 $\sigma(\cdot)$ 을 사용하는 multiple binary classification 으로 채택한다. 간단하게 sigmoid 의 출력은 $\sigma$ 로 표시된다.
제안된 classification-IoU 결합 표현은 전체 이미지에 대한 밀집된 supervision 들이 요구되고, class 불균형 문제는 아직 발생 되므로, Focal Loss 의 idea 를 물려 받아야 한다.
그러나 현재 ${\rm FL}$ 의 form 은 단지 $\{1, 0\}$ discrete label 들 이지만, 새로운 label 에는 소수가 포함된다.

따라서 결합 표현 ( joint representation ) 의 경우, 훈련을 성공적으로 가능하게 하기 위해 ${\rm FL\;(Focal Loss)}$ 의 두 부분을 확장시킨다.

${\rm CE}$ 파트 $-\log(p_t)$ 는
${\rm CE} : H(p, q) = -\sum_{i}p_i \cdot \log(q_i) = -\left(p_i \cdot \log(q_i) + (1-p_i)\cdot \log(1-q_i)\right)$
이와 같이 나타낼 수 있으므로, 완전한 버전 $-((1-y)\log(1-\sigma) + y \log(\sigma))$ 으로 확장된다.
scaling factor 파트 $(1-p_t)^{\gamma}$ 는 estimation $\sigma$ 와 그것의 연속적인 label $y$ 사이의 absolute 거리로 일반화 시킨다.
$i.e., |y - \sigma|^\beta (\beta \geq 0)$
여기서 $\mid \cdot \mid$ 는 non-negativity 를 보장한다.

이어서 두 개의 확장된 부분들을 조합하여 Quality Focal Loss ${\rm (QFL)}$ 라는 용어로써 완전한 loss 개체를 공식화한다.
$\mathbf{QFL}(\sigma) = -|y-\sigma|^{\beta}\left((1-y)\log(1-\sigma) + y\log(\sigma)\right)$
${\rm QFL}$ 의 global minimum 해는 $\sigma = y$ 로 정한다. ${\rm QFL}$ 는 $\beta$ 의 몇 가지 값들을 visualized 했다.

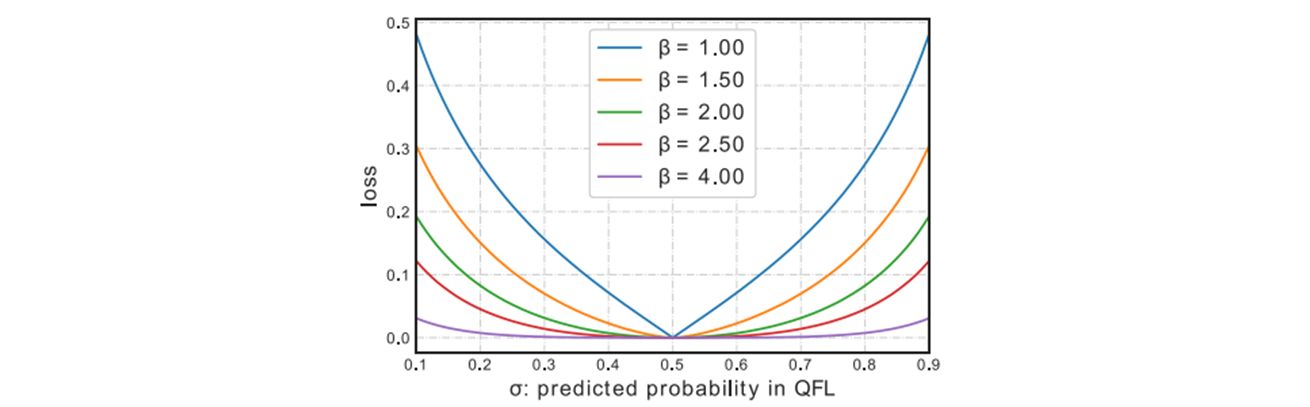
quality label 은 $y = 0.5$ 이다.
${\rm FL}$ 과 유사하게 ${\rm QL}$ 의 term $|y-Q|^{\beta}$ 는 modulating factor 로써 동작한다.
품질 추정이 정확하게 됨으로써, (예를 들어 $\sigma \rightarrow y$ ), factor 는 $0$ 이 되고, 잘 추정된 예시에 대한 loss 는 down-weighted 되며, 여기서 파라미터 $\beta$ 는 down-weighting 비율을 부드럽게 제어한다.

여기서도 실험에서 $\beta = 2$ 일 때 가장 잘 동작했다.

Distribution Focal Loss (DFL)

위치에서 bounding box 의 4 개의 측면 까지의 상대적인 offset 들을 regression targets 로 채택한다.

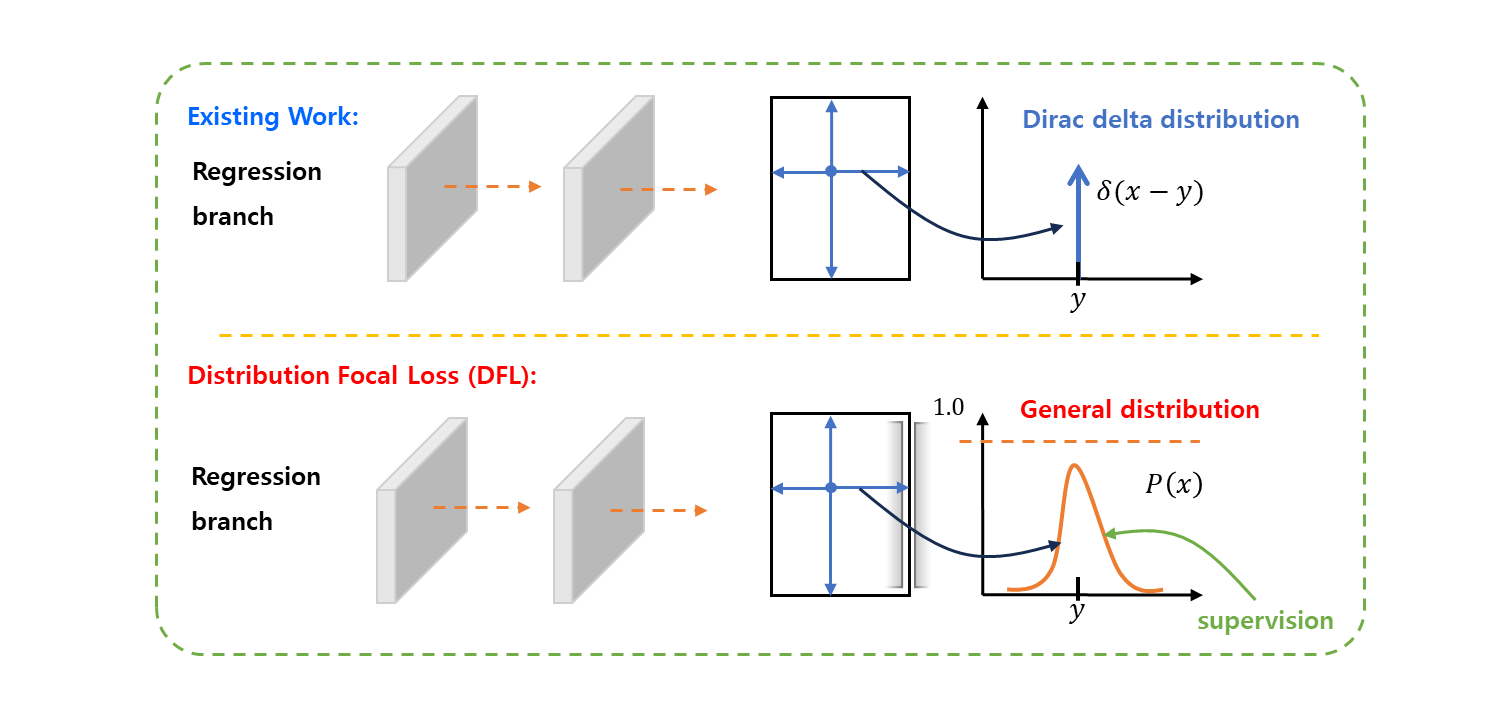
bounding box regressing 의 기존 연산들은 regressed label $y$ 를 Dirac delta 분포 $\delta(x-y)$ 로 모델링한다.
여기서 $\int^{+\infty}_{-\infty} \delta(x-y)dx = 1$ 을 만족하고, 보통 fully connected layers 를 통해 구현한다. 좀 더 공식적으로, $y$ 를 복구하는 적분의 형태는 다음과 같다.
$y = \int^{+\infty}_{-\infty} \delta(x-y)x dx$
분석에 따르면, Dirac delta 또는 Gaussian 가정들 대신에 어떠한 다른 priors 도입 없이 일반적인 분포 $P(x)$ 를 직접 학습하는 것을 제안한다.
label $y$ 의 range 는 최소값 $y_0$ 과 최대값 $y_n$ $(y_0 \leq y \leq y_n, n \in \mathbb{N}^+)$ 이고, 모델로부터 $\hat{y}$ 값을 추정할 수 있다. ( $\hat{y}$ 또한 $y_0 \leq \hat{y} \leq y_n$ )
$\hat{y} = \int^{+\infty}_{-\infty} P(x)x dx = \int^{y_n}_{y_0}P(x)x dx.$
CNN 과의 일관성을 위해 범위 $[y_0, y_n]$ 를 짝수 간격 ( 단순화를 위해 $\Delta = 1$ 을 사용 )인 $\{y_0, y_1, \cdots, y_i, y_{i+1}, \cdots, y_{n-1}, y_n\}$ 으로 통해서 연속적인 도메인에 대한 적분을 이산적으로 표현한다.
결과적으로, 이산적인 분포의 특성 $\sum^{n}_{i=0}P(y_i)=1$ 이 주어지면 추정 regression value $\hat{y}$ 는 다음과 같이 제시 될 수 있다.
$\hat{y} = \sum^{n}_{i=0}P(y_i)y_i$
결과적으로 $P(x)$ 는 $n+1$ 단위로 구성된 softmax $S(\cdot)$ 레이어를 통해 쉽게 구현될 수 있다. 여기서 단순화를 위해서 $P(y_i)$ 는 $S_i$ 로 표시된다.
$\hat{y}$ 는 SmoothL1, IoU Loss 또는 GIoU Loss 와 같은 전통적인 Loss 객체들을 사용하여 end-to-end fashion 으로 훈련 될 수 있다.
그러나 최종 적분 결과가 되는 $y$ 가 만들 수 있는 $P(x)$ 값의 조합들이 무한하여 학습의 효율성이 줄어들 수 있다.
직관적으로 ${\rm FL}$ 과 ${\rm QFL}$ 두 개 대비
${\rm FL}(p) = - (1-p_t)^{\gamma}\log(p_t), \; p_t= \begin{aligned} &\begin{cases} p & {\rm when} \; y=1 \\ 1-p & {\rm when} \; y=0 \end{cases} \end{aligned}$ $\mathbf{QFL}(\sigma) = -|y-\sigma|^{\beta}\left((1-y)\log(1-\sigma) + y\log(\sigma)\right)$
분포
$y = \int^{+\infty}_{-\infty} \delta(x-y)x dx$
는 bounding box 추정에 대해서 compact 하고 좀 더 (명확하고 정밀한) confident 하고 precise 한 경향이 있다.
이것은 목표 $y$ 에 가까운 값의 높은 확률을 명시적으로 장려함으로써 $P(x)$ 의 모양을 최적화 하도록 동기부여를 한다.
- “coarse label” 은 대략적인 또는 초기의 추정치를 의미
- “underlying location” 은 더 정확한 위치를 의미
뿐만 아니라, 가장 적절하게 기초가 되는 위치 (underlying location)가 존재하는 경우, 대략적으로 정해진 (coarse) label 에서 멀지 않은 경우가 종종 있다.

어떤 대상의 위치를 찾는 문제에서, 대략적으로 정해진 label 근처에 가장 적절한 위치가 있을 가능성이 높다는 말.

따라서 $y_i$ 와 $y_{i+1}$ ( $y$ 에 가장 가까운 두개, $y_i \leq y \leq y_{i+1}$ ) 의 확률들을 명시적으로 확대하기 위하여 네트워크가 label 근처의 값들에 신속하게 초점을 맞추도록 하는 ${\rm DFL}$ 을 도입한다.
bounding boxes 의 학습으로 클래스 불균형 문제의 위험 없이 단지 positive 샘플들을 대상으로 하므로, ${\rm DFL}$ 의 정의를 위해 ${\rm QFL}$ 에서의 complete cross entropy 부분을 간단히 적용.
${\rm DFL}(S_i, S_{i+1}) = -\left((y_{i+1}-y)\log(\mathcal{S}_i) + (y-y_i)\log(\mathcal{S}_{i+1}) \right)$
직관적으로, ${\rm DFL}$ 은 target $y$ 주위의 값들의 확률들을 확대하는데에 초점을 맞추는 것을 목표로 한다. ( 예를 들어, $y_i$ 와 $y_{i+1}$ ).
${\rm DFL}$ 의 global minimum 해는 예를 들어 $\mathcal{S}_i = \frac{y_{i + 1}-y}{y_{i+1}-y_i}$ , $\mathcal{S}_{i+1} = \frac{y-y_i}{y_{i+1}-y_i}$ 이고, 추정되는 regression 목표 $\hat{y}$ 는 해당 label $y$ 에 무한히 가까운 것을 guarantee 할 수 있다. 예를 들어서

$\hat{y} = \sum^{n}_{j=0}P(y_j)y_j = \mathcal{S}_iy_i + \mathcal{S}_{i+1}y_{i+1} = \frac{y_{i+1}-y}{y_{i+1}-y_i}y_i + \frac{y-y_i}{y_{i+1}-y_i}y_{i+1} = y$

loss function 으로써 정확성도 보장한다.
- ${\rm DFL}(S_i, S_{i+1}) = -\left((y_{i+1}-y)\log(\mathcal{S}_i) + (y-y_i)\log(\mathcal{S}_{i+1}) \right)$
- $y_i = y_l, \; y_{i+1} = y_r, \;\mathcal{S}_i = p_{y_l} = P(y_l), \;\mathcal{S}_{i+1} = p_{y_r} = P(y_r)$ where $\mathcal{S}$ = softmax
- ${\rm DFL}(P(y_l), P(y_r)) = -\left((y_r-y)\log(P(y_l)) + (y-y_l)\log(P(y_r)) \right)$

@staticmethod
def _df_loss(pred_dist, target):
    """
    Return sum of left and right DFL losses.

    Distribution Focal Loss (DFL) proposed in Generalized Focal Loss
    https://ieeexplore.ieee.org/document/9792391
    """
    tl = target.long()  # target left
    tr = tl + 1  # target right
    wl = tr - target  # weight left
    wr = 1 - wl  # weight right
    return (
        F.cross_entropy(pred_dist, tl.view(-1), reduction="none").view(tl.shape) * wl
        + F.cross_entropy(pred_dist, tr.view(-1), reduction="none").view(tl.shape) * wr
    ).mean(-1, keepdim=True)

target left 에 +1 을 하면 target right 이 되는 이유는, 위의 DFL 에서도 설명 했듯이, 연속적 도메인에 대한 적분을 이산적으로 표현 했으므로, left 와 right 구간을 1 이라는 이산적인 숫자로 정의했기 때문이라고 생각한다.

$\log(P(y_l))$
```
F.cross_entropy(pred_dist, tl.view(-1), reduction="none").view(tl.shape)
```
cross entropy 로 pred_dist 와 tl 분포의 cross entropy 를 구한다.
$(y_r-y)$
```
wl = tr - target
```
$\log(P(y_r))$
```
F.cross_entropy(pred_dist, tr.view(-1), reduction="none").view(tl.shape)
```
cross entropy 로 pred_dist 와 tr 분포의 cross entropy 를 구하여

(y - y_{l})

wr = 1 - wl = 1 - (tr - target) = 1 - tr + target = target - tl

General distribution

“대체 일반 분포 $P(x)$ 로 놓으면 어떤 아무 분포도 된다는 이야기냐?..”

BaseModel 에서의 loss function 에서 batch 만큼의 img 를 model 의 forward 에 넣는다.
predict 함수로 예측 값을 뽑아낸다.

# class BaseModel(nn.Module):

def forward(self, x, *args, **kwargs):
    """
    Forward pass of the model on a single scale. Wrapper for `_forward_once` method.

    Args:
        x (torch.Tensor | dict): The input image tensor or a dict including image tensor and gt labels.

    Returns:
        (torch.Tensor): The output of the network.
    """
    if isinstance(x, dict):  # for cases of training and validating while training.
        return self.loss(x, *args, **kwargs)
    return self.predict(x, *args, **kwargs)

# . . .

def loss(self, batch, preds=None):
    """
    Compute loss.

    Args:
        batch (dict): Batch to compute loss on
        preds (torch.Tensor | List[torch.Tensor]): Predictions.
    """
    if not hasattr(self, "criterion"):
        self.criterion = self.init_criterion()

    preds = self.forward(batch["img"]) if preds is None else preds
    return self.criterion(preds, batch)

v8DetectionLoss 의 call function 을 호출하여

# class DetectionModel(BaseModel):

def init_criterion(self):
    """Initialize the loss criterion for the DetectionModel."""
    return E2EDetectLoss(self) if self.end2end else v8DetectionLoss(self)

preds 예측 값을 기반으로 pred_distri 예측 분포를 뽑는다.

# class v8DetectionLoss:
def __call__(self, preds, batch):
    """Calculate the sum of the loss for box, cls and dfl multiplied by batch size."""
    loss = torch.zeros(3, device=self.device)  # box, cls, dfl
    feats = preds[1] if isinstance(preds, tuple) else preds
    pred_distri, pred_scores = torch.cat([xi.view(feats[0].shape[0], self.no, -1) for xi in feats], 2).split(
        (self.reg_max * 4, self.nc), 1
    )