[ Wasserstein ] 1. Prerequisite

d4r6j·2024년 7월 28일

ml-modeling

methodology-ai

목록 보기

4/8

axiom of completeness

완비성 공리 in Real number $\mathbb{R}$ (실수계) 부터 시작.

$X$ 가 $\mathbb{R}$ 의 공집합이 아닌 부분집합 이라 하자.

bounded

$\forall x \in X$ 에 대하여 $a \geq x$ 인 $\exist \;a \in \mathbb{R}$ 일 때 $X$ 를 위로 유계 (bounded above) 라 하고, $a$ 를 $X$ 의 상계 (upper bound) 라고 한다.
$\forall x \in X$ 에 대하여 $b \leq x$ 인 $\exist \; b \in \mathbb{R}$ 일 때 $X$ 를 아래로 유계 (bounded below) 라 하고, $b$ 를 $X$ 의 하계 (lower bound) 라고 한다.
$X$ 가 bounded above 인 동시에 bounded below 일 때는 간단히 $X$ 를 유계 (bounded) 라 한다.

supremum

이때 다음 조건을 만족하는 $a \in \mathbb{R}$ 를 $X$ 의 상한 또는 최소 상계 라고 한다.

$a$ 는 $X$ 의 least upper bound (상계) 이다. $(\sup \; X = a)$
$b$ 가 $X$ 의 upper bound 이면 $a \leq b$ 이다. 즉, $a$ 는 상계 중 제일 작은 것이다.

infimum

이때 다음 조건을 만족하는 $a \in \mathbb{R}$ 를 $X$ 의 하한 또는 최대 하계 라고 한다.

$a$ 는 $X$ 의 greatest lower bound (하계) 이다. $(\inf \; X = a)$
$b$ 가 $X$ 의 lower bound 이면 $a \geq b$ 이다. 즉, $a$ 는 하계 중 제일 큰 것이다.

axiom of completeness

$\mathbb{R}$ 이 완비성공간이라는 것을 이야기하고, $\mathbb{R}$ 에서만 성립하는 공리.

$X$ 가 $\mathbb{R}$ 의 공집합이 아닌 부분집합이고, 위로 유계 이면 반드시 $X$ 의 상한 $\sup X$ 가 존재.
$X$ 가 $\mathbb{R}$ 의 공집합이 아닌 부분집합이고, 아래로 유계 이면 반드시 $X$ 의 하한 $\inf X$ 가 존재.

completeness

일단 close set 으로 이해. topology 에서 정의는 좀 더 들어가야한다.

거리 공간 $(X, d)$ 에 대해 $A \subset X$ 라고 하자.

Cauchy sequence.
$(X, d)$ 상의 Cauchy sequence 이 수렴하는 점들이 $X$ 에 속하면 $(X, d)$ 는 complete.
Closure.. 등등..

cauchy sequence ( 코시 수열 )

$\forall \; \epsilon > 0$ 에 대하여 $m, n \geq N$ 이면,

|x_m-x_n| < \epsilon

을 만족하는 자연수 $N$ 이 존재할 때, 수열 $\{x_n\}$ 은 Cauchy sequence 라고 한다.

그렇다면.. 실수 공간이 아니라 어떤 space 이면? 그것이 distribution 이라면?

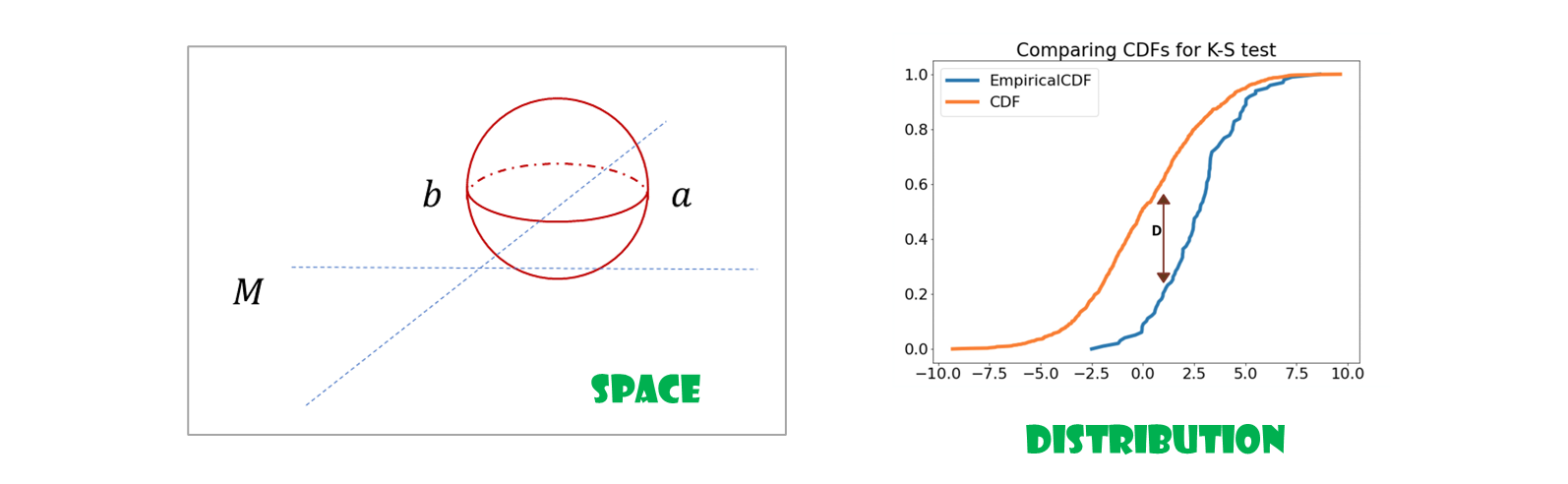
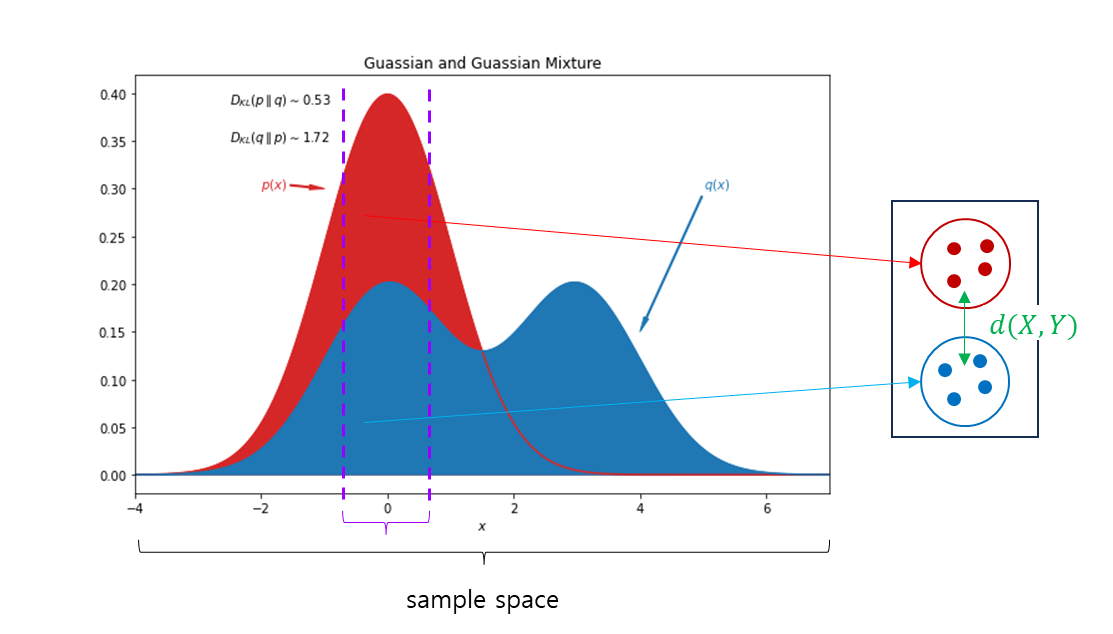
KS statistics ( TV : Total Variation 과 비슷 )

D = \sup_x\mid F_n(x) - F(x) \mid

measurable 값의 차이가 가장 큰 값.

contraction for distributions

고정된 learning rate $\eta$ 의 경우, stochastic gradient descent $(SGD)$ 는 state vector $w$ 를 사용하는 Markov process 이다.
이 과정의 점근적인 (asymptotic) 특성들에 관하여 많은 연구가 있지만, 점근적인 체계가 가정될 때 까지 필요한 반복 횟수에 관하여 많이 알려져 있지 않다.
점의 매핑 (mappings of points) 에서 분포의 매핑 (mappings of distributions) 으로 축약 (contractions) 의 개념을 확장함으로써 후자를 다룬다.

mappings of points

유클리디안 ( Euclidean ) 거리 : 변수들의 차이를 제곱하여 합산한 거리.

가장 일반적인, 물리적인 거리.

$D(X, Y) = \sqrt{\sum^{n}_{i=1}(X_i-Y_i)^2}$

$d_{12} = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2} = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}$

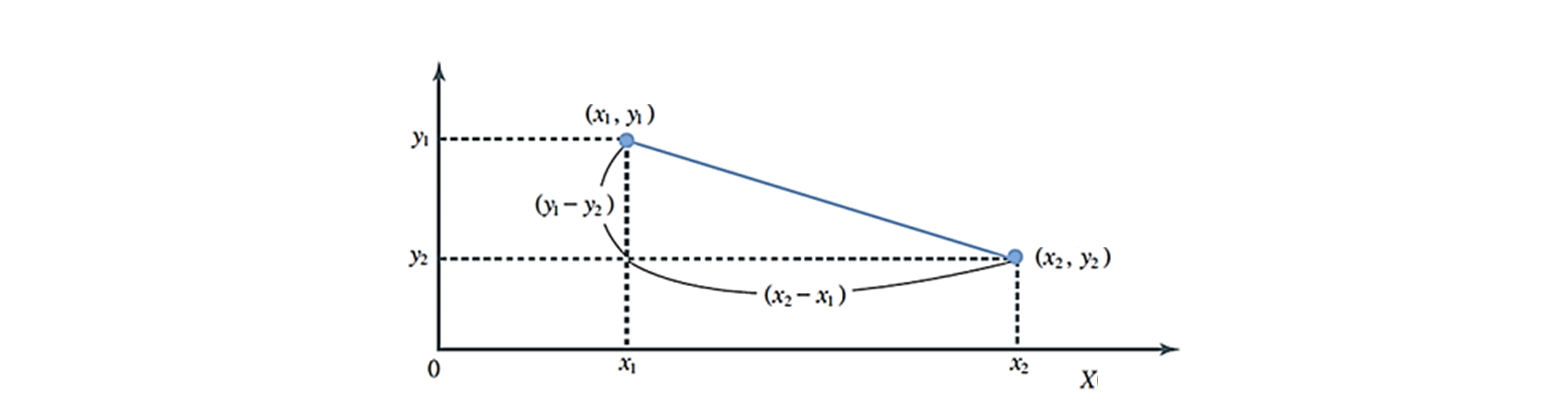
맨하튼 거리 ( Manhattan distance ) : 변수 값들의 차이를 절대값화 하여 합한 거리 측정

초록색이 Euclidean distance.

$D(X, Y) = \sum^n_{i=1}|X_i-Y_i|$
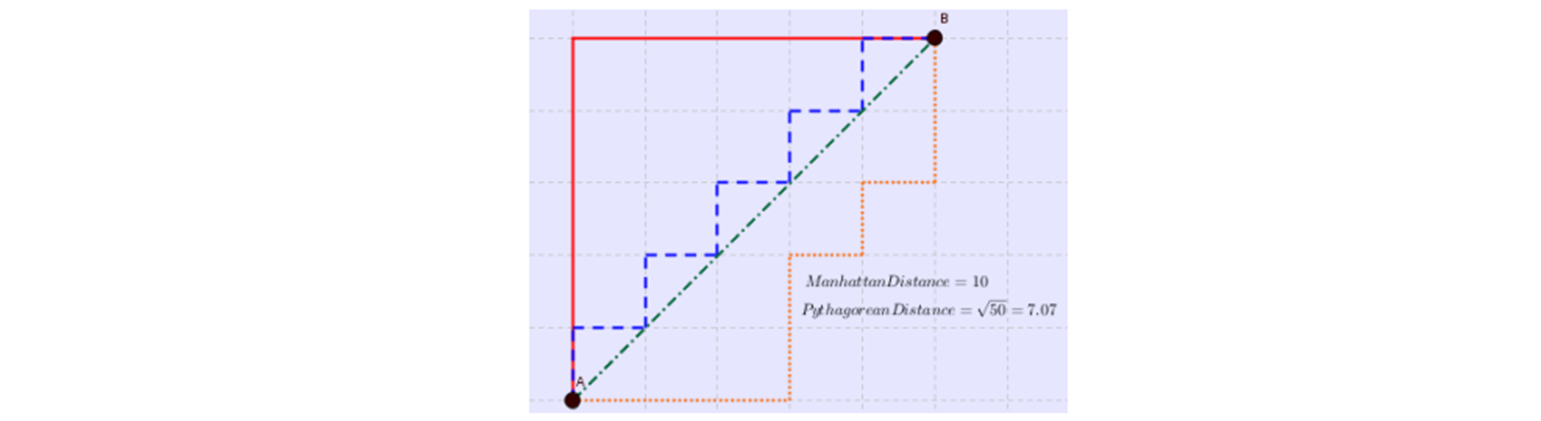
- green : 유클리디안 거리
- blue & red : 맨하튼 거리
Minkowski distance : Euclidean distance general version.

$D(X, Y) = \left(\sum^n_{i=1} |X_i - Y_i|^m \right)^{\frac{1}{m}}, \quad m>0$
- 제곱 대신 $m$ 을 사용하게 된다.
- 유클리디안 ( Euclidean ) 거리, 맨하튼 ( Manhattan ) 거리 의 일반화
- 거리를 산정하는 일반식, 함수에 포함된 지수들을 조정해 줌으로써 다양한 방식의 거리 측정.

mappings of distributions

$def :$ distance
- $d(x, y) \geq 0$
- $d(x, y) = 0 \rightarrow x = y, \quad x=y \rightarrow d(x,y) = 0$
- $d(x,y) = d(y,x)$ : symmetric
- $d(x,y) \leq d(x, z) + d(z, y)$
Kullback-Leibler divergence
- $d(x, y) \neq d(y,x)$
- $d(x, y) \nleq d(x,z) + d(z,y)$
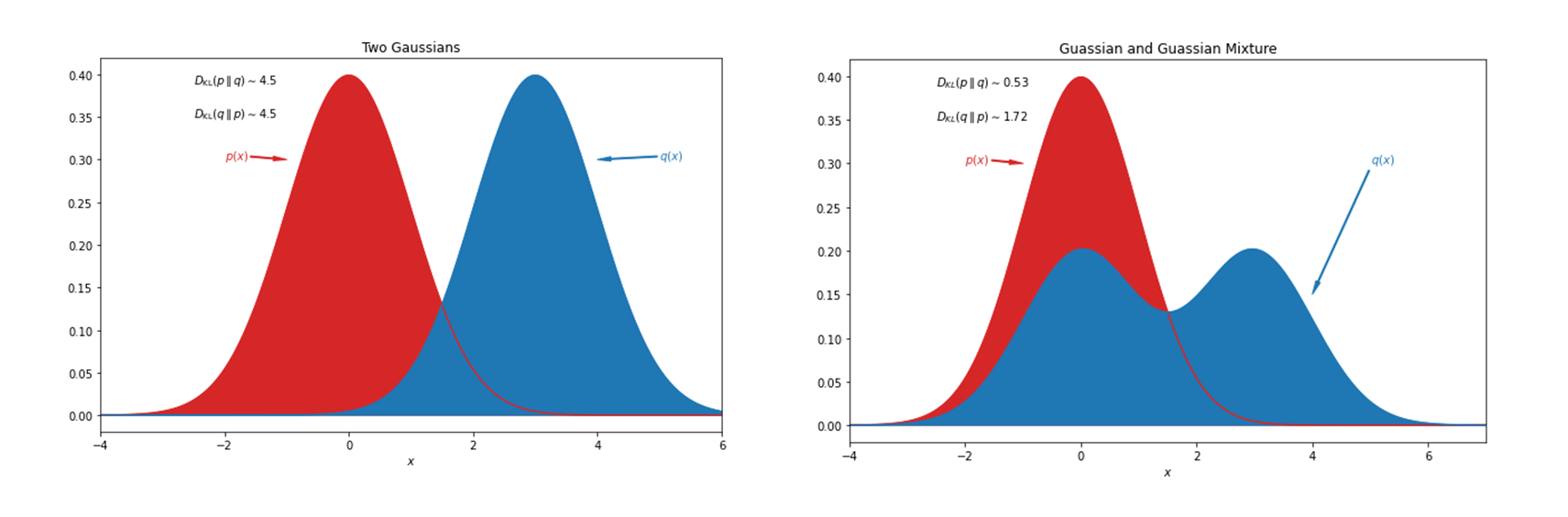
- $D_{KL}(p \parallel q)$ , $D_{KL}(q \parallel p)$ 값을 보면 좌측의 Two Gaussians 는 같지만, 우측의 Guassian and Guassian Mixture 는 다르다.

wasserstein metric

Radon-nikodym 의 정리 생각나네.. 기하 통계 봐야하는데..

for a radon space

Radon space $(M, d)$

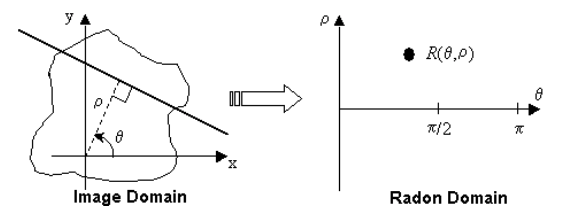
$P(M,d)$ 는 공간에 대한 모든 분포의 집합 이라고 하자.

$X, Y \in P(M,d)$ 두 분포 사이의 Wasserstein distance 는 아래와 같다.

W_{z}(X, Y) = \left[ \inf_{\gamma \in \Gamma(X, Y)} \int_{x, y}d^{z}(x, y)d\gamma(x, y)\right]^{\frac{1}{z}}

여기서 $\Gamma(X,Y)$ 는 marginals $X$ 와 $Y$ 를 포함한 $(M,d) \times (M,d)$ 에 대한 확률 분포들의 집합.

$\Gamma(X, Y) :$ 두 확률 분포 $X, Y$ 의 joint dist 들의 집합
$\gamma$ : 그 중 하나 $z$ : 지수 조정 → 다양한 방식으로 거리 조정.

= \inf_{\gamma \in \Gamma(X,Y)} \mathbb{E}^{\gamma}[d(X, Y)]

$d(X, Y)$ 의 expectation 을 가장 작게 추정한 값.

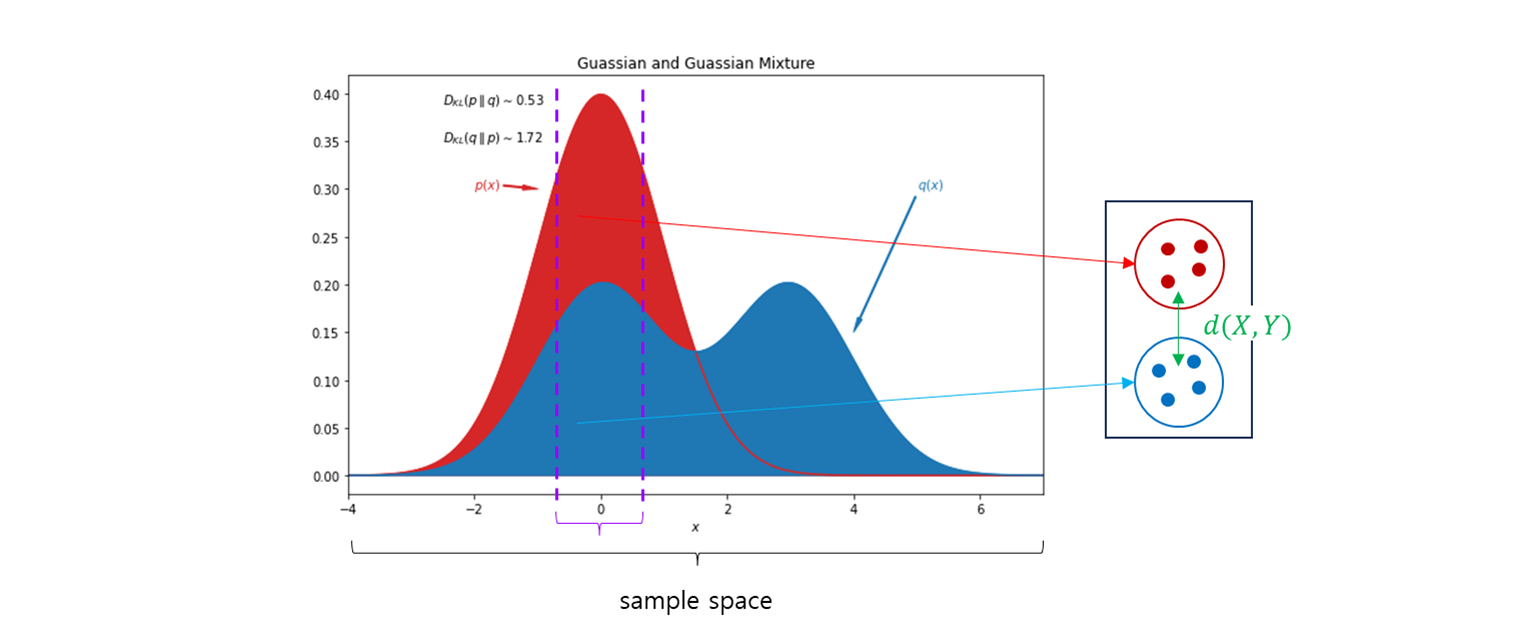
explain

$X(a) = (0, Z_{X}(a)),\; Y(a) = (\theta, Z_{Y}(a))$
$d(X, Y) = (|\theta-0|^2 + |Z_{X}(a) - Z_Y(a)|^2)^{\frac{1}{2}} \geq|\theta|$

${\rm if} : Z_X = Z_Y \rightarrow d(X, Y) = |\theta|$ → infimum..

Wasserstein metric 은 두 가지 매우 중요한 속성이 있다.
1. complete (완비성) 을 의미한다.
2. $(M,d)$ 에 있는 축약은 $(P(M,d), W_z)$ 에 있는 축약을 유도한다 (induces).

measure theory, and next !!

$\phi : M \rightarrow M$ 매핑이 주어지면

$M$ 에 pointwise $\phi$ 로 적용하여 $P(M,d) \rightarrow P(M,d)$ 를 구성할 수 있다.

$X \in P(M,d)$ 와 $X' := \mathbf{p}(X)$ 라 하자.

모든 특정 가능한 이벤트 $E$ 에 대해서 $\phi^{-1}(E)$ 에 의한 pre-image $\phi^{-1}(E)$ 를 나타낸다.

그 다음 $X'(E) = X(\phi^{-1}(E))$ 를 갖는다.

이 형태는 많이 봤다.

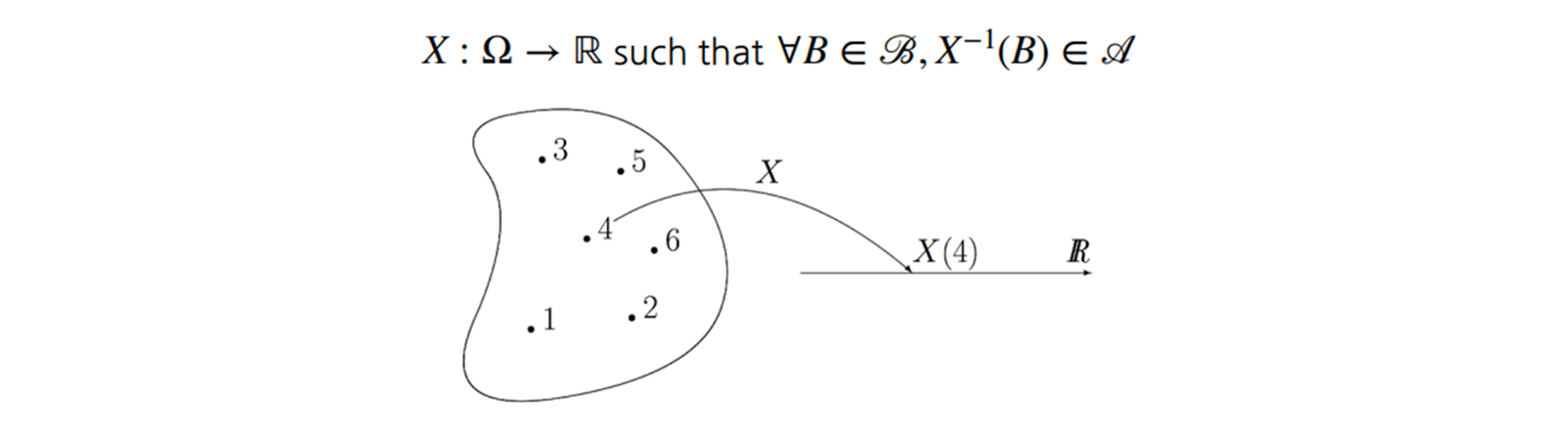
Random Variable 와 Distribution, 그리고 Optimal transport . . .

transformer 기하 내용도 봐야하고, metric, loss 도 더 연구를 해야하고, entropy 개념도 정리하고, 현재 잘 나오는 SOTA 논문도 보고, 시스템, 제품 개발도 해야하는데.. 세상의 속도는 너무 빨리 앞으로 나간다. 정말 다들 너무 잘 따라간다.. ㅎㅎ 열심히 해야지!