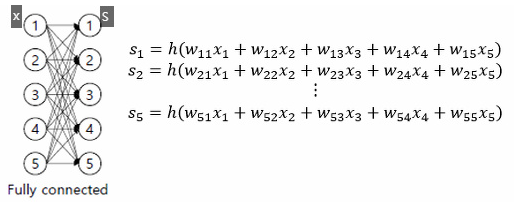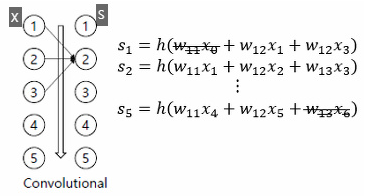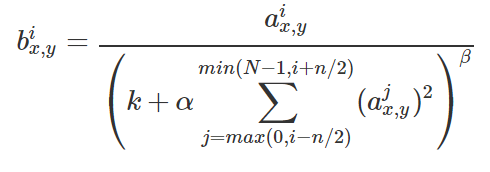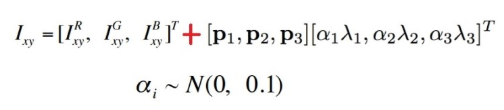ImageNet Classification with Deep Convolutional Neural Networks

DIYA
작성자: 이상민

ImageNet Classification with Deep Convolutional Neural Networks

Alex Krizhevsky, Ilya Sutskever, Geoffrey E. Hinton

Abstract

1. 120만개의 고해상도의 이미지를 1000개의 다른 클래스로 분류를 위해 크고 심층적인 CNN을 훈련시켜 사용하였다.
2. Test dataset에서 이전보다 37.5% 향상되어 오류율 17.0%을 달성하였다.
3. AlexNet의 기본 구조: 5개의 CNN으로 구성된 6천만 개의 매개변수, 65만개의 뉴런
   → 포화상태가 아닌 뉴런을 빠르게 학습하기 위해서 효율적인 GPU를 사용하였다.
   → 그 중 일부는 최대 풀링 레이어와 최종 1000방향 소프트맥스를 가진 3개의 Fully-connected로 구성된다.
4. 과적합을 줄이기 위한 정규화 방법으로는 Dropout을 사용하였다.

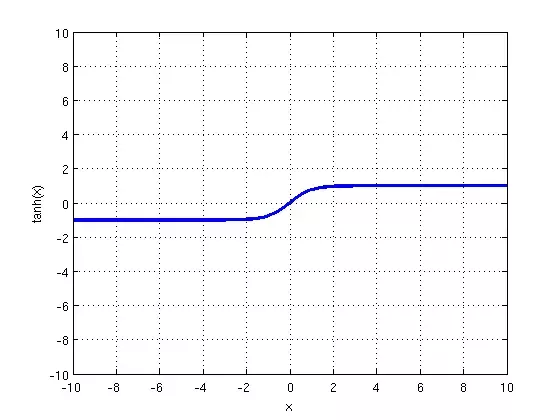
그림1 : non-saturating neurons (포화상태가 아닌 뉴런)

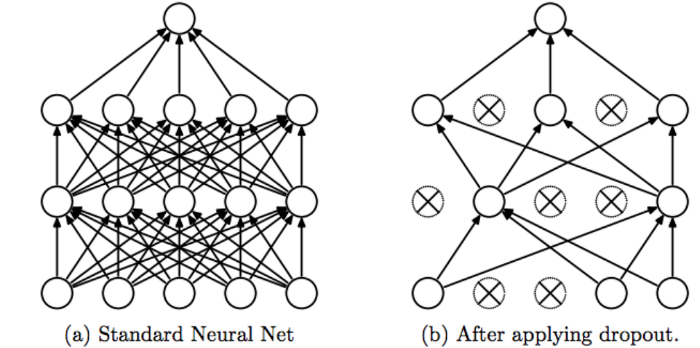
그림2 : Dropout의 예시
(a) Dropout을 하지 않은 Fully-connected의 예시
(b) Dropout을 사용하여서, 과적합을 줄이는 과정의 예시

1. Introduction

2012년도의 객체 인식에 대한 접근 방식은 기계학습 방법을 필수적으로 사용한다.

객체 인식의 성능을 높이기 위해서 더 큰 데이터셋을 수집하고, 더 강력한 모델을 학습하고, 과적합을 방지하기 위해 더 좋은 기술을 사용한다.

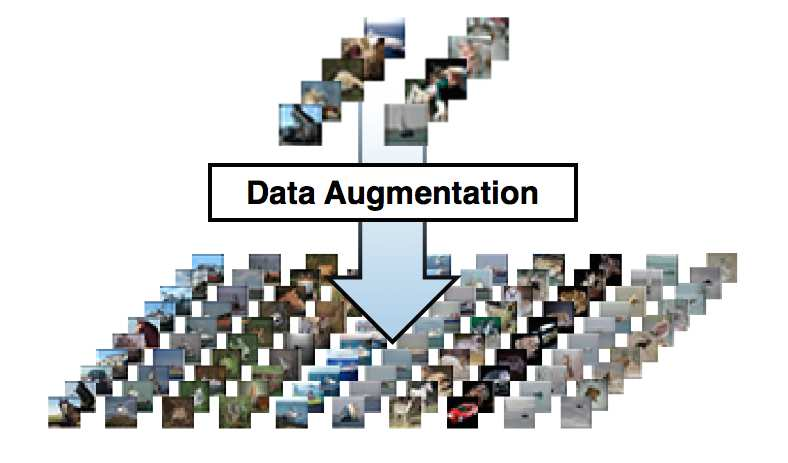
최근까지 라벨링된 이미지의 데이터셋은 수만개의 이미지에서 그쳤지만, 라벨 보존 변환(label-preserving transformations)으로 증강하여서 데이트셋만들기 때문에 인식작업을 잘 해결할 수 있게되었다.

그림 3 : Data Augmentation (DA) artificially inflates data-sets using label preserving transformations.
출처 : Improving Deep Learning using Generic Data Augmentation

하지만, 현실의 객체는 상당한 가변성을 보이기 때문에, 이를 인식하기 위해서는 훨씬 더 큰 데이터셋을 학습하여야한다. 그리고 실제로 작은 데이터셋의 단점은 널리 인식되어 왔다. (수백만 개의 이미지로 레이블이 지정된 데이터셋을 수집할 수 있게 된 것은 최근이다.)

수백만 개의 이미지에서 수천 개의 개체를 학습하기 위해서는 학습 능력이 큰 모델이 필요하다. 하지만 객체 인식 작업의 엄청난 복잡성은 imagenet만큼 큰 데이터셋으로도 지정할 수 없다는 것을 의미하기 때문에 우리의 모델은 우리가 가지고 있지 않은 모든 데이터를 인식하기 위한 많은 사전 지식도 가지고 있어야한다.

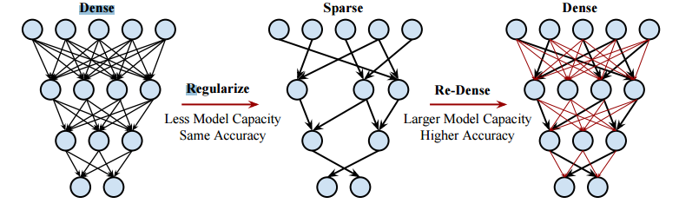
CNN(Convolutional Neural Network)은 그러한 모델 클래스 중 하나를 구성하며[16, 11, 13, 18, 15, 22, 26], 이들의 용량은 깊이와 폭을 변화시켜 제어할 수 있다.

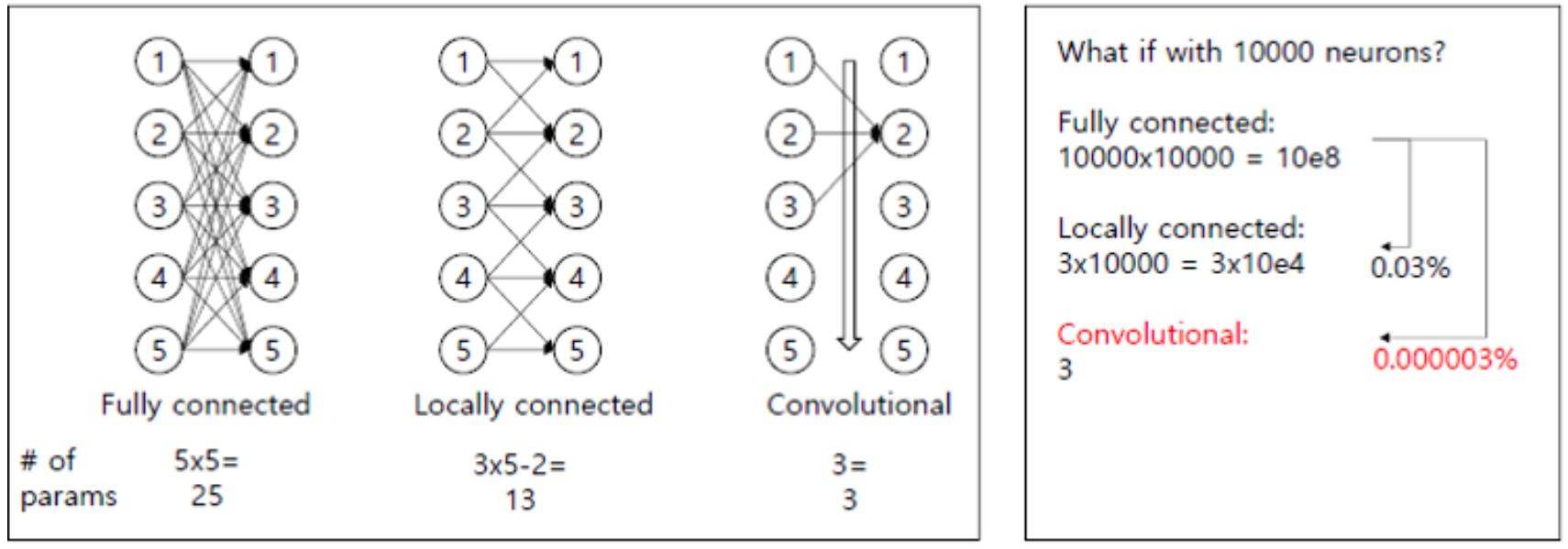
따라서, 기존의 DNN방식의 fully-connection 방식보다 sparse connection 구조를 갖는 CNN 모델로 인해 더 적은 parameter로 효율적으로 학습시킬 수 있게 되었다.

💡 CNN이 DNN보다 이미지 영역의 학습에서의 효율적인 이유
1. Weight parameter의 감소
2. Weight sharing & Sparse connection
3. Translation equivariance and Translation invariance
4. Translation invariance
5. Overfitting

1. Weight parameter의 감소

그림5 : DNN과 CNN의 첫 번째 단계에서 필요한 가중치 수

DNN의 Fully-connection을 사용한다면, 가중치의 수가 기하급수적으로 많아지고, 이로 인해서 위치만 다른 객체의 이미지를 인식하지 못 할 가능성이 커지며, 최종적인 학습결과가 기존의 tranning dataset과 별반 다른점 없다는 문제점과, 학습과정에서 Over fitting이 발생하여 tranning dataset과도 다르다고 나타낼수 있다는 문제점이 있습니다.
위와 같은 문제점을 극복하기 위해서 CNN에서는 Weight parameter를 감소시켜 학습시킵니다.

2. Weight sharing & Sparse connection

DNN에서는 하나의 출력값을 위해 각각 다른 가중치 들이 사용되고 있다. (입력값이 항상 동일)
하지만, CNN은 하나의 출력값에 같은 가중치 들이 사용되고 있다. (입력값이 항상 바뀐다.)

그림8 : parameter sharing

Weight sharing을 통한 연산은 CNN sparse connection 구조를 형성할 수 있게 기여했습니다.
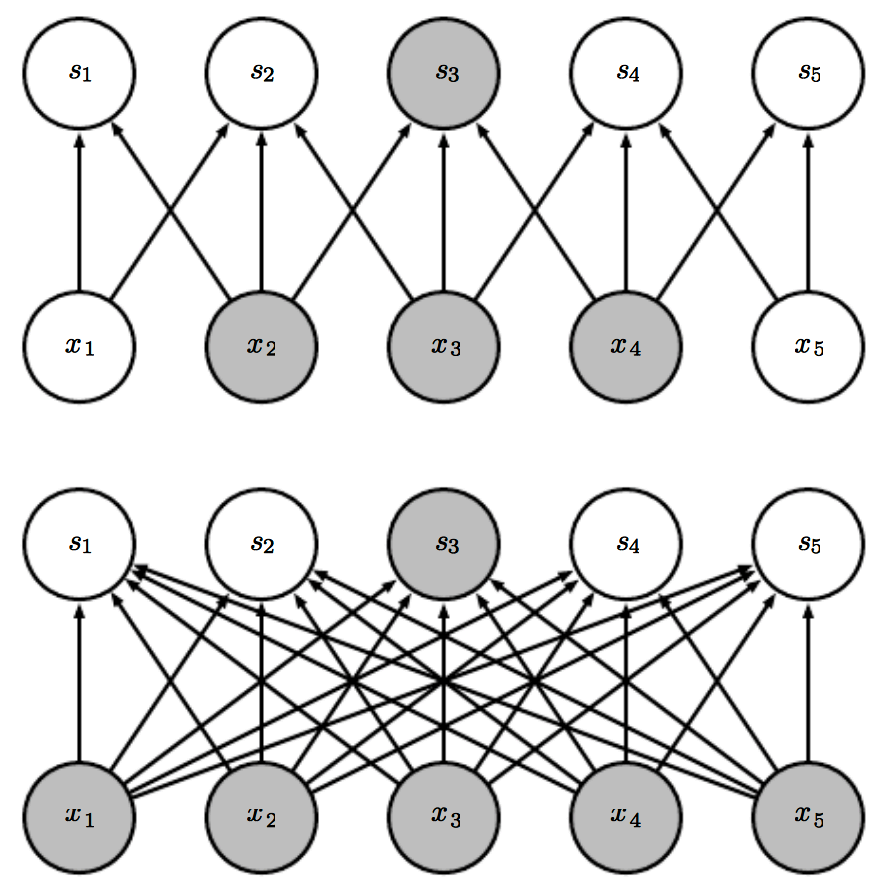
전체 이미지에서 Convolution filter을 적용시켜 연산할 때, conv filter가 적용되지 않은 부분은 모두 0이라고 할수 있으며, 0이 의미하는 바는 아래 그림 7처럼 가중치가 모든 입력이미지에 대해서 연결되어 있지않고, sparse하게 연결되어 있다는걸 의미합니다.

이러한 특성때문에 CNN은 sparse connection 구조를 가지고 있다고 말할 수 있습니다.

그림6 : DNN 구조

그림7: CNN 구조

그림8: 가중치를 적게 사용하면서도 좋은 성능을 낼 수 있는 CNN구조의 예시.

3. Translation equivariance and Translation invariance

Translation equivariance의 정의
"Specifically, a function f(x) is equivariant to a function g if f(g(x)) = g(f(x)). In the case of convolution, if we let g be any function that that translates the input, that is, shifts it, then the convolution function is equivariant to g."

f = convolution 연산을 수행하는 함수

g = translate을 시키는 함수

💡 convolution(translate(x)) = translate(convolution(x))
convolution filter를 적용시킨 것을 이동 시킨 결과와 전체 이미지를 이동시킨 것을 convolution filter 연산을 한 결과와 같다는 의미이다.

예를 들어, input = [0,3,2,0,0] 이라고 가정하고, convolution 연산을 적용시킨 결과는 [0,1,0,0]로 가정하여서 설명하겠습니다. [0,1,0,0]을 오른쪽으로 translate하면 [0,0,1,0]이 나오며, 전체 이미지가 이동된 [0,0,3,2,0]에 convolution 연산을 적용한다면, [0,0,1,0]이 나오게 됩니다.

결과적으로, 입력 이미지의 위치가 변하면 "동일하게" 출력값도 같이 변한다는 의미를 갖습니다.

그래서 Equivariance하다는 뜻을 입력이 변하면 출력도 입력이 변한정도와 동일하게 바뀌는 현상을 의미합니다.

4. Translation invariance

그림8 : Translation invariance

우측 6개의 이미지를 convolution 한 결과로 얻은 feature map은 숫자 8의 위치에 따라 다르게 표현되었지지만, translation eqvariance 특성으로 인해 입력값이 이동한 것에 따라 출력값이 변했기 때문에, 숫자 8이라는 부분의 출력값만을 보았을 때 출력값으 Pattern은 변하지 않을 것입니다.

위와 같은 특징으로 인해서 CNN모델은 Translation invariance의 특징을 가지게 됩니다.
이로인해 CNN은 DNN에 비해 적은 양의 학습 이미지로 학습을 할 수 있다는 장점을 가지게 됩니다.

5. Overfitting

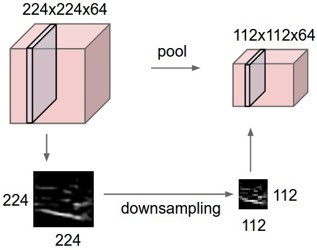
그림9: Pooling의 Downsampling

pooling의 downsampling을 반복해서 진행하면서, 가까이서 보았을 때에는 달라보이지만, 멀리서 보았을 때에는 비슷해 보이는 현상을 이용하여서 학습할 이미지에 대해서 특징만으로 객체를 구분함으로써 Overfitting을 방지합니다.

CNN의 엄청난 상대적 효율성에도 불구하고, 그것들을 고해상도 이미지에 대규모로 적용하는데에는 엄청난 비용이 들었지만, 다행히 2D convolution의 구현을 GPU를 통해 훈련을 용이하게 할 수 있게 되었으며, imagenet과 같은 최신 데이터 세트에는 Overfitting 없이 모델을 학습시킬 수 있는 충분한 레이블이 지정된 예가 포함되어 있다.

Section 3 에서는 성능 향상과 학습시간 감소를 위한 기술들이 설명되어 있으며,

Section 4 에서는 Overfitting을 방지하기 위한 기술들에 대해 설명되어있다.

최종 네트워크의 구조는 5개의 Convolution Layer와 3개의 Fully-connected Layer로 구성 되어있다.

최종 네트워크의 크기는 현재 GPU에서 사용할 수 있는 메모리의 양과 용인가능한 훈련 시간에 의해 제한되었기 때문에, 추후의 더 빠른 GPU와 더 큰 데이터셋의 사용이 가능해진다면, 네트워크의 결과가 개선될 수 있다고 생각한다.

요약 : 이전의 모델들의 간단한 recognition은 해결할 수 있었지만, 다양한 물체에 대한 recognition이 어려워 CNN이 출현하게 되었다. CNN의 구조(Layer의 크기, filter의 크기)는 GPU성능에 제한이 있다.

2. The Dataset

ILSVRC라는 대회의 참가하여 성능 평가를 하였으며, ILSVRC에서의 데이터셋은 1000개의 카레토리에 약 1000개의 이미지가 포함된 ImageNet의 하위 집합을 사용합니다.

전체적으로 약 120만개의 훈련이미지, 5만개의 검증 이미지, 15만개의 테스트 이미지가 있습니다.

section 6에서는 테스트셋 레이블을 사용할 수 없는 데이터 세트의 대한 결과를 설명합니다.

ImageNet은 가변 해상도 이미지로 구성되어 있기 때문에 이를 CNN에서 사용하기 위해서는 일정한 사이즈의 입력을 넣어주어야 하여서, (Fully-connection Layer에서 softmax activation function으로 fully connection으로 만들어주기 위해서 입력 크기를 일정하게 입력해줍니다.) 256*256 size로 downsampling을 조정하고, 먼저 짧은 면의 길이가 256이 되게 한 다음 중앙을 기준으로 256의 길이를 뺀 나머지를 crop 해주었다.

그림10: Data Preprocessing

또한, 일반화성능을 향상시키기 위해서 입력 이미지의 raw RGB pixel들을 학습시켰습니다.
이를 수행하기 위해 학습 이미지데이터들을 normalization 해주는 방법으로 전체 학습이미지 Dataset의 픽셀 평균들을 빼주었다.

학습이미지 - dataset 평균 = normalized 학습 이미지

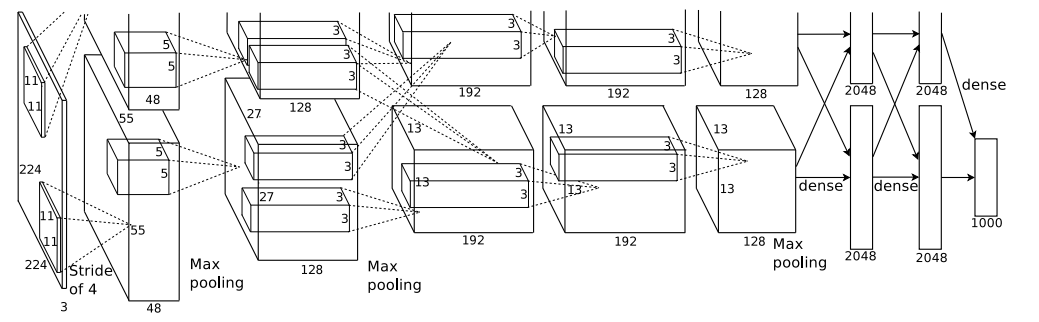
3. The Architecture

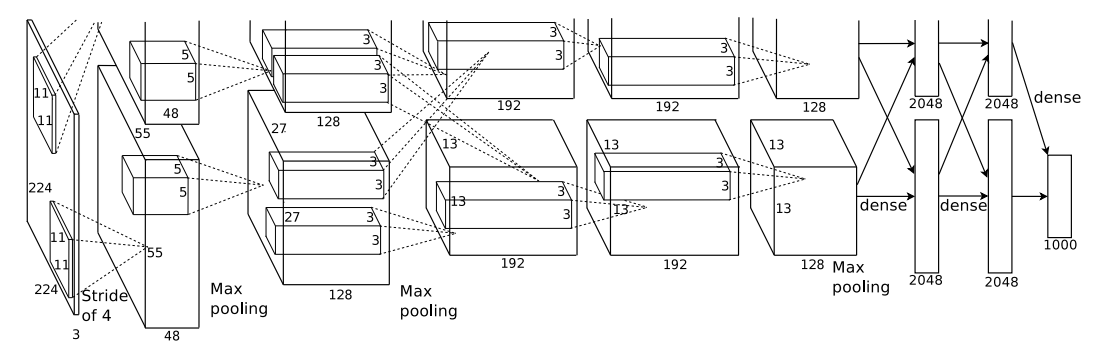
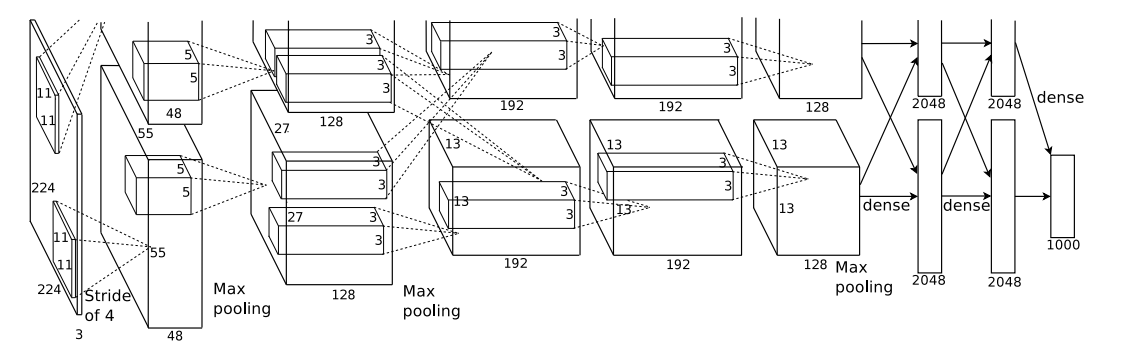
그림11 : AlexNet Network Architecture

AlexNet은 이전 CNN 구조에서 사용했던 activation function을 ReLU로 변경하였다.

GPU를 병렬적으로 사용하여 CNN을 학습시켰으며,

추가적으로 Local Response Normalization 방법을 사용했으며,

그리고 기존에 사용하던 pooling 방식과 조금 다른 overpooling방식을 사용하였습니다.

8개의 학습된 Layer에서 5개의 convolution과 3개의 Fully-connected Layer를 포함하고 있다.

3-1부터 3-4까지 중요도 순으로 설명하였다.

3.1 ReLU Nonlinearity

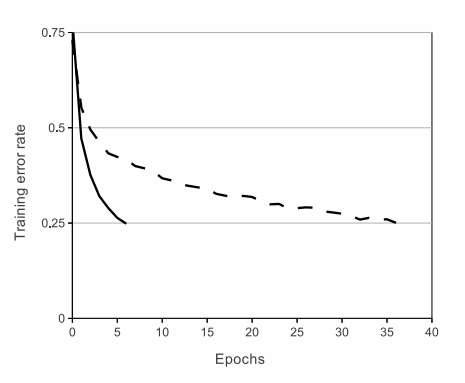
그림12: ReLU(solid line)와 tanh(dashed line)의 active function으로 사용했을 때의 error rate 차이

입력 $x$의 함수로 뉴런의 출력 $f$를 모델링하는 표준 방법은 $f(x)=tanh(x)$ 또는
$f(x)=(1+e^{-x})^{-1}$이다.

In terms of training time with gradient descent, these saturating nonlinearities are much slower than the non-saturating nonlinearity f(x) = max(0, x).

기울기 강화를 사용한 훈련 시간 측면에서, saturating nonlinearities(포화 비선형성)은 non-saturating nonlinearity(비수축 비선형성)보다 훨씬 느리다.

💡 non-saturating nonlinearity 함수는 어떤 입력 x가 무한대로 갈때 함수의 값이 무한대로 가는 것을 의미하고 saturating nonlinearity 함수는 어떤 입력 x가 무한대로 갈때 함수의 값이 어떤 범위내에서만 움직이는 것을 의미합니다.

saturating nonlinearities라는 용어는 vanishing gradient(사라져 가는 경사도) 유발할 수 있는 nonlinear activation function(비선형 활성화 함수)을 의미한다. 예를 들어, $f(x)$라는 함수가 있을 때 $x$라는 정의역이 무한대로 증가되거나, 무한대로 감소되면 $f(x)$값이 0 or 1로 포화되기 때문에 붙여진 이름이다.

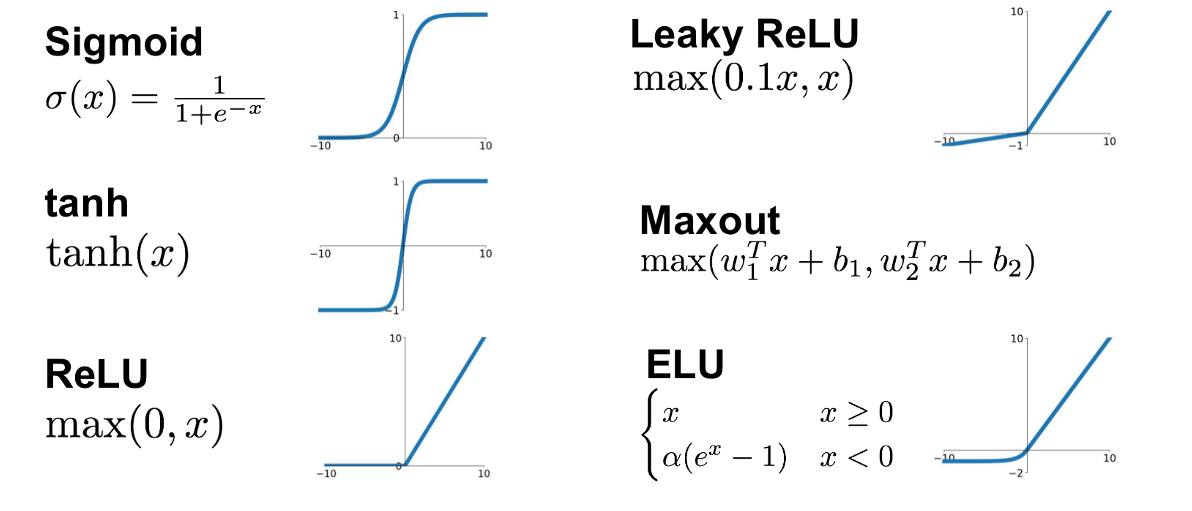
그림13 : Active function의 종류에 따른 그래프

3.2 Traning on Multiple GPUs

CNN연산들을 GPU로 계산함으로써 학습속도도 좀 더 빠르고 error rate를 줄일 수 있습니다.

여기서 전체 conv filter(kernel)을 반으로 나누어서 계산하였습니다.
예를 들어 100개의 filter가 있다면 50개는 A part로 남은 50개는 B part로 할당하여서 서로 독립적으로 연산할 수 있도록 설정하였으며,

그림14

위의 그림14의 conv단계를 거칠때에는 반으로 나누는것은 계속해서 진행하지만, 독립적으로 실행되던 filter를 서로 뒤섞여서(communication) 쓰일수 있도록 설정하였습니다.

3.3 Local Response Normalization

ReLU는 포화(saturating)현상을 피하게 해주는 활성 함수(activation function)이다.

예를 들어, Sigmoid function 같은 경우는 input data의 속성이 서로 편차가 심하면 포화(saturating)되는 현상이 심해서 나중에 vanishing gradient을 유발할 수 있게 됩니다.

때문에 ReLU를 사용하여서 vanishing gradient을 피할 수 있게 합니다.

본 논문에서는 Lateral inhibition의 개념을 언급하면서 local response normalization의 필요성을 언급하고 있습니다. Lateral inhibition은 강한 자극이 주변의 약한 자극을 전달하는 것을 막는 효과를 말한다.

그림15

이 수식을 정리하면 아래와 같이 표현할 수 있습니다.

그림16

$a$는 이미지상의 특정 $x,y$ 위치에 있는 i번 째 conv filter가 적용된 결과값을 의미합니다.

예를 들어, $n=5, i=5$라고 설정했다면, 5번째 conv filter 결과 값은 3,4,5,6,7번째 conv filter의 결과값을 이용해 정규화 한다는 것을 의미한다.

예를 들어, 3,4,5,6,7번째 conv filter의 결과 값이 매우 높다면 i번째 conv filter가 적용된 결과값도 매우 작아지게 된다. 5번째 conv filter 결과 값이 3,4,6,7번째 conv filter값 결과보다 매우 높다면 상대적으로 3,4,6,7번째 conv filter 결과 값은 작아질 것을 의미하는 것이다.

이러한 과정을 통해서 강한 자극이 약한 자극의 세기를 죽이게 되는 결과를 얻게 되는 것 입니다.

그 외 hyperparameter들은 validation dataset을 통해 경험적으로 최적의 값들을 얻었다.

위와 같은 과정으로 CIFAR-10 dataset에 실험한 결과 기존 CNN을 정규화없이 진행하였을 때의 error rate 13% 였지만, Local Response Normalization을 통해서 test error rate를 11%로 줄일 수 있었다.

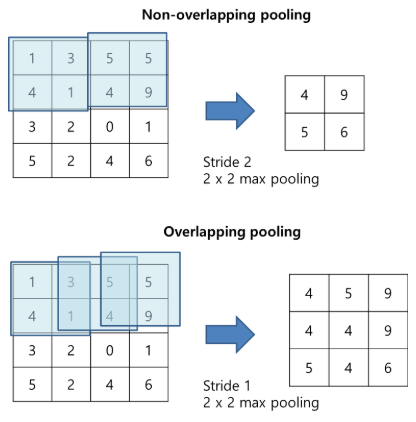
3.4 Overlapping Pooling

그림17: Overlapping pooling의 과정.

s(stride), z(pooling을 통해 얻어지는 feature size)를 의미하며,

s = z를 설정하면 CNN에서 일반적으로 사용되는 기존의 로컬 pooling을 얻을 수 있으며,

s < z를 설정하면 overlapping pooling의 결과를 얻을 수 있습니다.

4x4 feature map을 pooling 한다고 했을 때, s =1로 설정하고 z를 3(3x3)이라고 설정하게 되면 위와 같이 overlapping해서 pooling하게 됩니다. 이러한 연산을 통해 top-1, top-5의 error rate를 0.4%까지 줄였다.

3.5 Overall Architecture

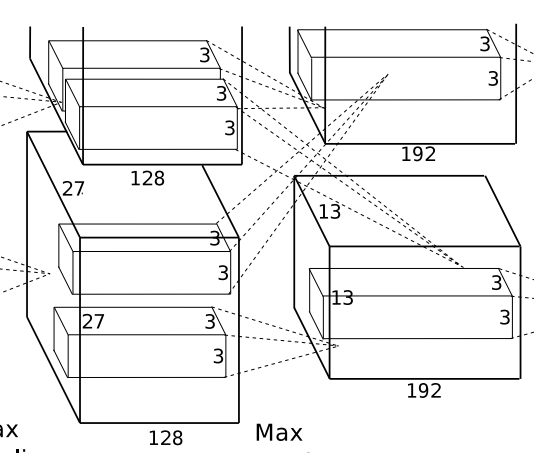
그림18:

CNN의 전체 구조이다. 2,4,5번째의 conv layer은 동일한 GPU에 있는 이전 계층의 커널맵에게만 연결되며, 3번째 conv layer는 2번째 conv layer와 모두 연결되며, fully-connected layer에서는 이전 층의 모든 뉴런과 연결됩니다.

section 3.4 에서 설명한 Overlapping pooling은 Response normalization layer 모두에 적용됩니다.

ReLU Nonlinearity은 모든 conv layer와 fully-connected layer에 출력에 적용됩니다.

첫 번째 컨볼루션 레이어는 4픽셀의 stride로 11×11×3 크기의 96개의 커널을 가진 224×224×3 입력 이미지를 필터링한다.

두 번째 컨볼루션 레이어는 첫 번째 컨볼루션 레이어의 (응답 정규화 및 풀링) 출력을 입력으로 가져와서 크기 5 × 5 × 48의 256 커널로 필터링한다.

세 번째, 네 번째 및 다섯 번째 컨볼루션 레이어는 어떤 개입된 풀링 또는 정규화 레이어 없이 서로 연결되어 있다.

세 번째 컨볼루션 레이어는 크기가 3 × 3 × 256인 384개의 커널을 두 번째 컨볼루션 레이어의 (정규화된, 풀링된) 출력에 연결한다.

네 번째 컨볼루션 레이어는 크기가 3 × 3 × 192인 384개의 커널을 가지고 있으며,

다섯 번째 컨볼루션 레이어는 크기가 3 × 3 × 192인 256개의 커널을 가지고 있다. 완전히 연결된 층은 각각 4096개의 뉴런을 가지고 있습니다.

4. Reducing Overfitting

CNN 아키텍쳐는 6천만개의 매개 변수를 가지고 있다.

ILSVRC의 1000개 클래스는 각 훈련 예제를 이미지에서 레이블로 매핑하는데 10비트의 제약을 가하지만, 이는 상당한 과적합 없이 그렇게 많은 매개 변수를 학습하기에는 불충분한것으로 밝혀졌다.

그래서 과적합을 피하기 위한 두가지 방법에 대해서 설명합니다.

4.1 Data Augmentation

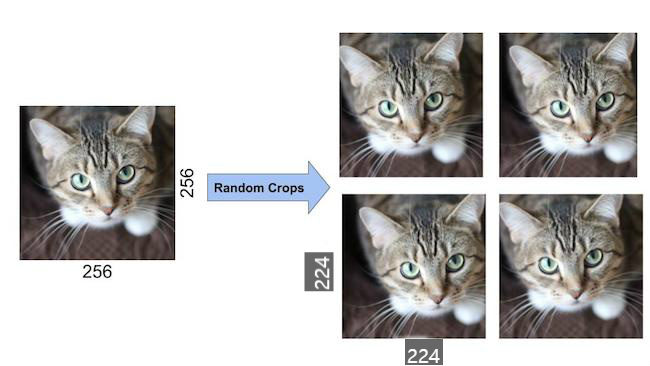
현재 갖고 있는 데이터를 좀 더 다양하게 만들어 CNN 모델을 학습시키기 위해 만들어진 개념이다.

그리고 label-preserving transformations을 하여서 상하반전같은 기법을 사용할 때의, 의미가 완전히 바뀌는 것을 방지합니다.

첫 번째 형태의 방식으로 적은 데이터를 다양한 데이터로 만들어주어 Overfitting을 피하게 해주는 효과를 가지고 있습니다.

그림19: Data preprocessing의 과정에서 Random Crop의 결과.

두 번째 형태의 데이터 확대는 훈련 이미지에서 RGB 채널의 강도를 변경하는 것으로 구성된다.

그림20: PCA를 RGB에 적용

그림21:

그림22: PCA on RGB 예시

각 훈련 이미지에 발견된 주성분의 배수를 평균 0과 표준 편차 0.1의 가우스에서 추출한 임의의 변수 시간에 비례하는 크기로 추가한다.

여기서 $P_i$와 $\lambda_{i}$는 고유 벡터와 RGB 픽셀 값의 고유값이다.

위의 예시로 인해서 입력 이미지가 224 x 224 x 3차원인 이유를 알 수 있습니다.

4.2 Dropout

Dropout을 통해서 학습 시간을 줄이고, Overfitting도 피할 수 있습니다.

0.5의 확률로 숨겨진 뉴런의 출력을 0으로 설정하며, 이렇게 탈락된 뉴련은 전진 패스에 기여하지 않으며, 역 전파에서 참여하지 않습니다.

아래의 그림에서 Dropout이 사용된 곳은 마지막 dense의 두 부분에서 사용되었습니다.

그림23

5. Details of learning

그림24

그림23에 나와있는 첫번째 input의 224x224 사이즈는 논문의 설정된 stride와 padding을 고려했을 때, Layer을 거쳐 13x13에 도달하려면 227x227의 사이즈가 맞습니다.

6. Results

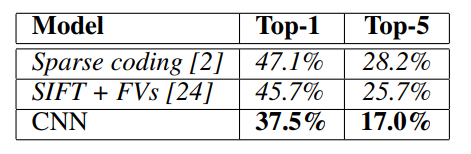
그림25

AlexNet의 결과가 기존의 recognition(classification)의 모델 'Sparse coding', 'SIFT+FVs'보다 더 향상 되었음을 알 수 있다.

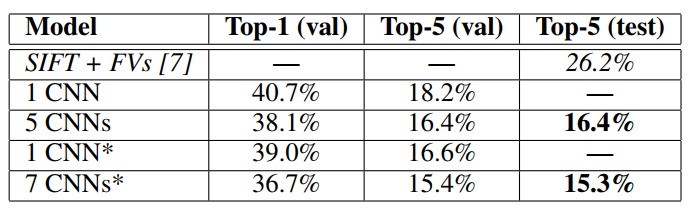
그림26

1CNN은 해당 논문에서 언급한 모델들의 validation set, test set에 대한 error rate을 언급하고 있으며

5CNNs는 해당 논문에서 비슷한 모델들의 prediction(classification) 평균을 내어서 error rate를 계산하였으며, 표시가 있는 1CNN은 pre-traning, fine tunning 기법들이 사용된 AlexNet의 error rate이고, 7CNN은 앞서 언급한 '5CNN'과 2개의 유사한 구조를 같은 pre-trained and fine-tuned alexnet의 prediction 평균을 낸 error rate이다.

6.1 Qualitative Evaluations

그림27 : ILSVRC-2010 test image와 AlexNet에서의 가장 가능성이 높은 것으로 간주되는 5개의 label.

그림28: ILSVRC-2010 test 영상입니다.

7. Discussion

CNN을 사용하여서 매우 어려운 dataset에서 기록을 깨는 결과를 달성할 수 있었다.

경험적으로, 중간 계층을 하나 제거하면 네트워크 상위 1개의 성능에서 약 2%의 손실이 발생하게 된다. 따라서 해당 모델의 깊이는 상당히 중요한 요소로 작동한다.

지금까지, 해당 논문의 결과는 네트워크를 더 크게 만들고 더 오래 훈련시켰기 때문에 향상되었지만,
human visual system의 초점을 맞추기 위해서는 더 큰 크기와 순서를 갖추어야 한다.

궁극적으로, 정적 이미지에서 누락되거나, 비디오와 같은 동적인 이미지에서의 덜 분명하지만 매우 유용한 정보를 제공하는 Dataset에 CNN을 사용하고 싶다는 점을 나타냈다.

Reference

https://89douner.tistory.com/60
https://naknaklee.github.io/classification/2020/04/22/AlexNet-Post-Review/
https://89douner.tistory.com/58
https://89douner.tistory.com/42
https://nanonets.com/blog/data-augmentation-how-to-use-deep-learning-when-you-have-limited-data-part-2/
https://darkpgmr.tistory.com/110
https://89douner.tistory.com/22
https://nittaku.tistory.com/267
https://d2l.ai/chapter_convolutional-modern/alexnet.html

Alexnet Code

def cnn_model_fn(features, labels, mode):

    """INPUT LAYER"""
    input_layer = tf.reshape(features["x"], [-1, FLAGS.image_width, FLAGS.image_height, FLAGS.image_channels], name="input_layer") #Alexnet uses 227x227x3 input layer. '-1' means pick batch size randomly
    #print(input_layer)

    """%FIRST CONVOLUTION BLOCK
        The first convolutional layer filters the 227×227×3 input image with
        96 kernels of size 11×11 with a stride of 4 pixels. Bias of 1."""
    conv1 = tf.layers.conv2d(inputs=input_layer, filters=96, kernel_size=[11, 11], strides=4, padding="valid", activation=tf.nn.relu)
    lrn1 = tf.nn.lrn(input=conv1, depth_radius=5, bias=1.0, alpha=0.0001/5.0, beta=0.75); #Normalization layer
    pool1_conv1 = tf.layers.max_pooling2d(inputs=lrn1, pool_size=[3, 3], strides=2) #Max Pool Layer
    #print(pool1_conv1)
    

    """SECOND CONVOLUTION BLOCK
    Divide the 96 channel blob input from block one into 48 and process independently"""
    conv2 = tf.layers.conv2d(inputs=pool1_conv1, filters=256, kernel_size=[5, 5], strides=1, padding="same", activation=tf.nn.relu)
    lrn2 = tf.nn.lrn(input=conv2, depth_radius=5, bias=1.0, alpha=0.0001/5.0, beta=0.75); #Normalization layer
    pool2_conv2 = tf.layers.max_pooling2d(inputs=lrn2, pool_size=[3, 3], strides=2) #Max Pool Layer
    #print(pool2_conv2)

    """THIRD CONVOLUTION BLOCK
    Note that the third, fourth, and fifth convolution layers are connected to one
    another without any intervening pooling or normalization layers.
    The third convolutional layer has 384 kernels of size 3 × 3
    connected to the (normalized, pooled) outputs of the second convolutional layer"""
    conv3 = tf.layers.conv2d(inputs=pool2_conv2, filters=384, kernel_size=[3, 3], strides=1, padding="same", activation=tf.nn.relu)
    #print(conv3)

    #FOURTH CONVOLUTION BLOCK
    """%The fourth convolutional layer has 384 kernels of size 3 × 3"""
    conv4 = tf.layers.conv2d(inputs=conv3, filters=384, kernel_size=[3, 3], strides=1, padding="same", activation=tf.nn.relu)
    #print(conv4)

    #FIFTH CONVOLUTION BLOCK
    """%the fifth convolutional layer has 256 kernels of size 3 × 3"""
    conv5 = tf.layers.conv2d(inputs=conv4, filters=256, kernel_size=[3, 3], strides=1, padding="same", activation=tf.nn.relu)
    pool3_conv5 = tf.layers.max_pooling2d(inputs=conv5, pool_size=[3, 3], strides=2, padding="valid") #Max Pool Layer
    #print(pool3_conv5)


    #FULLY CONNECTED LAYER 1
    """The fully-connected layers have 4096 neurons each"""
    pool3_conv5_flat = tf.reshape(pool3_conv5, [-1, 6* 6 * 256]) #output of conv block is 6x6x256 therefore, to connect it to a fully connected layer, we can flaten it out
    fc1 = tf.layers.dense(inputs=pool3_conv5_flat, units=4096, activation=tf.nn.relu)
    #fc1 = tf.layers.conv2d(inputs=pool3_conv5, filters=4096, kernel_size=[6, 6], strides=1, padding="valid", activation=tf.nn.relu) #representing the FCL using a convolution block (no need to do 'pool3_conv5_flat' above)
    #print(fc1)

    #FULLY CONNECTED LAYER 2
    """since the output from above is [1x1x4096]"""
    fc2 = tf.layers.dense(inputs=fc1, units=4096, activation=tf.nn.relu)
    #fc2 = tf.layers.conv2d(inputs=fc1, filters=4096, kernel_size=[1, 1], strides=1, padding="valid", activation=tf.nn.relu)
    #print(fc2)

    #FULLY CONNECTED LAYER 3
    """since the output from above is [1x1x4096]"""
    logits = tf.layers.dense(inputs=fc2, units=FLAGS.num_of_classes, name="logits_layer")
    #fc3 = tf.layers.conv2d(inputs=fc2, filters=43, kernel_size=[1, 1], strides=1, padding="valid")
    #logits = tf.layers.dense(inputs=fc3, units=FLAGS.num_of_classes) #converting the convolutional block (tf.layers.conv2d) to a dense layer (tf.layers.dense). Only needed if we had used tf.layers.conv2d to represent the FCLs
    #print(logits)

    #PASS OUTPUT OF LAST FC LAYER TO A SOFTMAX LAYER
    """convert these raw values into two different formats that our model function can return:
    The predicted class for each example: a digit from 1–43.
    The probabilities for each possible target class for each example
    tf.argmax(input=fc3, axis=1: Generate predictions from the 43 last filters returned from the fc3. Axis 1 will apply argmax to the rows
    tf.nn.softmax(logits, name="softmax_tensor"): Generate the probability distribution
    """
    predictions = {
      "classes": tf.argmax(input=logits, axis=1, name="classes_tensor"),
      "probabilities": tf.nn.softmax(logits, name="softmax_tensor")
      }
   
    #Return result if we were in prediction mode and not training
    if mode == tf.estimator.ModeKeys.PREDICT:
        return tf.estimator.EstimatorSpec(mode=mode, predictions=predictions)

    #CALCULATE OUR LOSS
    """For both training and evaluation, we need to define a loss function that measures how closely the
    model's predictions match the target classes. For multiclass classification, cross entropy is typically used as the loss metric."""
    onehot_labels = tf.one_hot(indices=tf.cast(labels, tf.int32), depth=FLAGS.num_of_classes)
    loss = tf.losses.softmax_cross_entropy(onehot_labels=onehot_labels, logits=logits)
    tf.summary.scalar('Loss Per Stride', loss) #Just to see loss values per epoch (testing tensor board)
    
    #CONFIGURE TRAINING
    """Since the loss of the CNN is the softmax cross-entropy of the fc3 layer
    and our labels. Let's configure our model to optimize this loss value during
    training. We'll use a learning rate of 0.001 and stochastic gradient descent
    as the optimization algorithm:"""
    if mode == tf.estimator.ModeKeys.TRAIN:
        optimizer = tf.train.AdamOptimizer(learning_rate=0.00001)
        train_op = optimizer.minimize(loss, global_step=tf.train.get_global_step()) #global_Step needed for proper graph on tensor board
        #optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.00005) #Very small learning rate used. Training will be slower at converging by better
        #train_op = optimizer.minimize(loss=loss,global_step=tf.train.get_global_step())
        return tf.estimator.EstimatorSpec(mode=mode, loss=loss, train_op=train_op)
    
    #ADD EVALUATION METRICS
    eval_metric_ops = {"accuracy": tf.metrics.accuracy(labels=labels, predictions=predictions["classes"])}
    return tf.estimator.EstimatorSpec(mode=mode, loss=loss, eval_metric_ops=eval_metric_ops)