Generative Model 시리즈3
알고가기
-
생성모델에 대한 기초적인 지식이 없다면 이 블로그를 추천한다.
-
Flow based model을 이해하기 위한 식
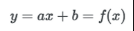
a는 scale, b 는 bias 이다.
이떄 역함수를 표현하는 방법은 아래와 같이 된다.

행렬에서도 똑같다.
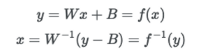
W는 scale 행렬, B는 bias 행렬이다.
-
y = Wx + B 처럼 벡터 공간(행렬)에서 선형변환(Linear Transformation) Wx과 Bias 행렬 B가 더해지는 변환을 Affine Transformation(아핀변환) 이라고 한다. 즉, Bias 행렬 B가 zero이면 선형성을 만족하고, B가 0이 아니면 비선형 변환이라고 할 수 있다.
그럼 생성모델을 만들때 우리는 최대한 특정 y = f(x)와 비슷한 잠재변수 z를 계산해 우리는 모델을 만든다.
그럼 아래와 같이 z를 이용해 x와 최대한 닮은 z를 계산할 수 있을 것이다.
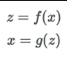
앞썬 시리즈에서 말했던 VAE는 Encoder/Decoder 구조를 가지고 있다. 이는 x = g(f(x))를 만족하도록 학습하는 비지도 학습에 해당되는데, VAE는 이 과정에서 z확률분포가 정규분포(Normalization distribution) 등 다루기 쉬운 확률분포를 닮게끔 학습되도록 한다는 것을 얘기했다. 하지만 Flow-based 모델은 조금 다르다.
Flow based 모델은 변수 x를 최대한 잘 표현할 수 있는 잠재변수 z를 계산하는 z = f(x)를 학습하되, f의 역함수 f-1를 이용해서 x를 계산하는 것이 목표이다.
-
변수 변환(Change of Variable)
여기서 우리는 변수 변환이라는 것을 아는 것이 중요하다. 변수 변환이란 f(x) = x - 1이라는 함수가 있을 때, x 대신에 t(시간)과 같은 새로운 변수를 넣어 x = 2t + 1 일때 f(t) = 2t 와 같은 다른 변수로 바꾸는 것을 변수 변환(Change of Variable)이라고 한다.
그럼 변수 변환을 알아보았으니 아까 말했던 확률분포를 닮은 역함수를 만들기 위한 flow based model에 대해 접그내호밪.
아까 말했던 변수 x와 x에 대해 확률 밀도 함수(PDF, Probablity Denstiy Function) 이 있다고 하자.
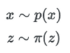
그럼 x와 최대한 비슷한 z에 대해서도 확률밀도함수 ㅠ(z) 가 있을 것이다.
우리가 가정한 변수 z가 변수 x를 잘표현하는 잠재변수일것이고, z의 확률밀도가 주어진다면, 일대일 매핑함수 x = f(z)를 사용해 새로운 변수를 구할 수 있을 것이라고 기대할 수 있다. 또한 함수 f가 가역적(Invertible)하다면, 역함수가 존재하다는 의미니까 z = f-1(x)도 가능할 것이다. 그럼 우리가 알아야할 것은 알려지지 않은 x의 확률 분포 함수 p(x)를 구하면 된다.
-
확률 분포의 정의
확률 분포에 대해 잘 모를 수 있으니 확률 분포에 대한 정의에 대해 알아보자.
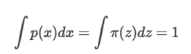
확률 분포함수 p(x)가 있을때 모든 구간에서 적분하면 1일 것이다. 그리고 잠재변수 z에 대한 확률 변수 ㅠ(z)에 대해서도 1일 것이다.
우리는 x = f(z)라는 변수 변환 함수와 함수 f가 가역적이라는 전제로 역함수 z = f-1(x)를 알고 있을 것이다. 위의 식에서 z 대신 아래와 같은 식으로 표현 가능하다.
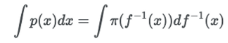
dz → f’-1(x), z → f-1(x)
그럼 이제 적분을 하면 p(x)에 대해 z로 표현가능해진다. 아래와 같이

이제 이를 우리는 행렬(Matrix)로 표현해보자. 어렵지 않다. 식에서 f에 대해 절대값씌워져있는건 determiant로 다른건 진한 z와 x로 표현하면 된다.
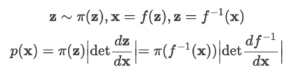
이제 딱 하나 남았다. 미분이다. 행렬을 미분한 형태인 도함수 행렬을 의미하는 자코비안 행렬(Jacobian Matrix)에 대해 알아보자.
-
자코비안 행렬(Jacobian Matrix)
자코비안 행렬, 말은 어려운데 별거 없다. 행렬의 미분 → 도함수의 미분 → 자코비안 행렬이다.
딥러닝 분야에서는 전부 Matrix를 활용한 연산이기 때문에, 단순한 변수가 아닌 행렬이라는 변수(?)를 미분한 것이라 생각하면 된다.
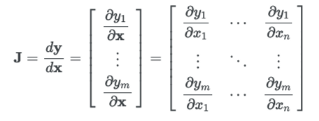
자코비안 행렬은 위의 그림과 같이 정의된다. 행렬이라는 변수안에는 여러 변수(scalar값)이 존재하고 이를 똑같이 미분한다고 생각하면 된다. 이를 모아서 도함수 행렬, 즉 자코비안 행렬이라고 하는 것이다. 또한, 기존 함수의 차원을 N차원이라고 했을때 자코비안 행렬한 경우 N-1차원을 가지고 이싿는 것 이 정도면 된다.
-
행렬식(Determinant)
행렬식에 대해 알아보자면 행렬이라는 변수 안에 들어가 있는 값을 곱과 합을 통해 연산한 값(스칼라 값)이라고 생각하면 된다.

여기서 중요한게 행렬식이 왜 들어가냐고 할 수 있는데 행렬식은 특정 성질을 가지고 있기 떄문이다. 그렇기에 딥러닝 모델을 볼때 |a| 나 det(a)와 같은 식이 보이면 모두, 하나의 값을 가지고 있다고 생각하면 된다. 아래는 행렬식의 주요 성질이다.

자 이제, 자코비안 행렬과 행렬식에 대해 알아보았으니 이제 본문 내용을 통해 우리가 알고싶었던 Flow based model에 대해 알아보자.
-
본문 내용
💡 잠재변수 z를 이용해 x에 대한 확률 밀도함수 p(x)에 대해 최대한 닮은 확률 밀도함수를 구하는 것이다. 이를 위해 역변환 함수이론을 이용해 PDF를 구할 것이다!‘알고가기’ 를 통해 x에 대한 확률밀도함수 p(x)를 잠재변수라고 가정한 z를 통해 추정할 수 있음을 확인했다. 그럼 p(x)를 추정한다는 것을 알아보았으니 Flow-based model에 대해 알아보자.
! 많은 테크블로그를 참고하여 짜깁기 하였으니, 이해가 어렵다면 다른 블로그를 알아보길 추천한다.
Flow-based model이란?

flow-based model이란 앞서 말했던 잠재변수 z를 활용한 x = f(z)와 잠재변수 z에 대한 확률밀도함수 p(z)가 주어졌을때
p(x)에 대해 최대한 비슷한 함수로 접근하는 것이다. → 즉 Px(x)를 구하는 것이라 할 수 있다.
Normalizing Flow = NF
NF란 우리가 Flow based model에서 사용하는 아이디어라고 생각하면 된다. NF는 데이터의 확률 분포를 예측하는데 효과적이라고 한다. NF는 앞서 말했던 역함수 함수를 이용해 실제 데이터의 확률분포와 가장 비슷한 확률 분포로 변환하는 것이 목표이다.
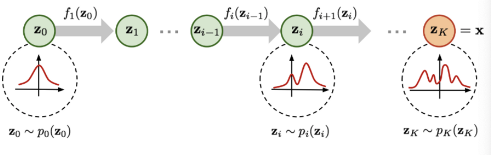
위의 그림을 보면 별거 없다. 처음(i = 0)일떄는 되게 단순해보이는데, 실제 데이터(x)의 확률 분포는 복잡하기에 f(z)라는 함수를 이용해 잠재변수 z로 x와 비슷한 확률 분포를 만들어 주는 것이 목표이다.
아래는 이에 대한 과정이다. (* 아이디어만 알고싶다면 스킵. 하지만 아래까지 정독을 권장한다.)
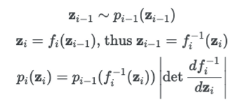
i라는 것만 추가되고 별거 없다 z ~ p(z) 이고, p(z) = (위의 사진의 마지막 식)으로 생각하면 된다.
이를 정리해서 p(z)에 대해 풀어보면 아래와 같은 식이 나온다.
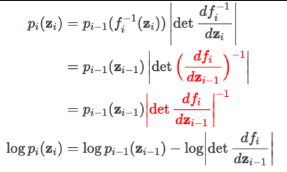
위의 사진에서 마지막에 log 씌워준 것은 보통 데이터들에 대해 너무 작은 값에 대해 곱이 아닌 덧셈/뺼셈으로 표현해 연산을 쉽게 위해 전체에 로그를 씌워준 것이다.
여기서 이제 이 모델의 꽃인 역함수 이론과 가역함수의 자코비안에 대해 표현한 식을 볼 수 있다.
-
역함수이론
만약 y = f(x)와 x = f-1(y)가 있다면,
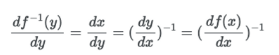
가 된다. 이때 역함수의 미분과 함수의 미분은 Inverse 관계라는 것을 알 수 있다. 따라서 역함수의 자코비안를 자코비안의 역으로 표현가능하다.
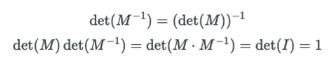
가역함수의 자코비안은 결국 가역행렬인 경우 행렬식의 특성을 가지고 있기에 빨간색 부분처럼 표현이 가능하게 된 것이다.

드디어 다왔다. 우리는 Z0의 확률 분포에서 시작해 K번의 역변환(Inverse Matrix)를 통해 x라는 확률분포를 구하는 식(logP(x))을 구할 수 있게 되었다.
- 단 NF 방식을 통해 구하려면 두 가지 조건이 충족되어야 한다. (=정독을 했으면 어느정도 감이 올 것이다.)
출처 및 참고 문헌
Flow based Model 에 대한 아이디어 논문
https://arxiv.org/pdf/1505.05770.pdf
수학적 과정 풀이
https://devkihyun.github.io/study/Flow-based-Generative-Models-1-Normalizing-Flow/
