[ML] 딥러닝의 깊이 있는 이해를 위한 머신러닝 14-1 (K-MOOC)

학습내용

• DNN 을 활용한 향상된 Supervised Learning

• Residual 구조의 의미

• 다양한 DNN 활용방법

학습목표

• 기존보다 향상된 형태의 Supervised Learning 을 위한 DNN 구조를 이해

• Residual 구조의 필요성 이해

• 다양한 DNN 활용방법을 이해

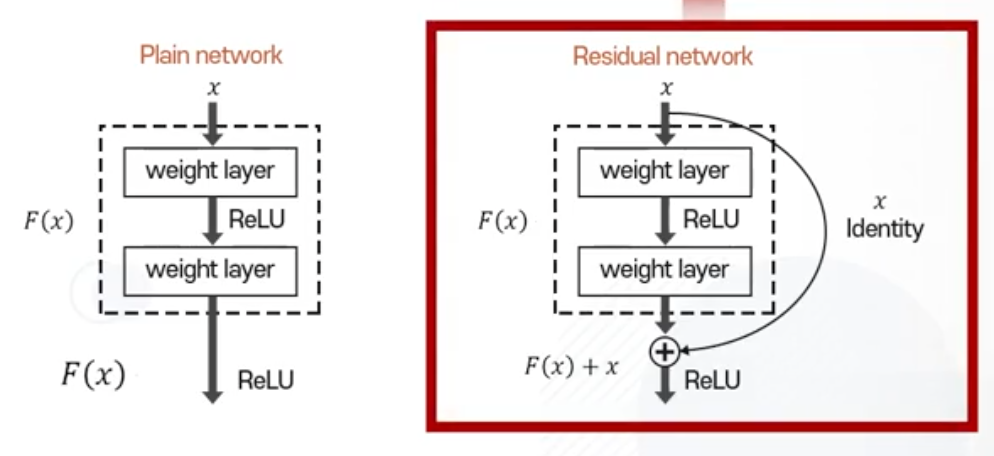
Residual Network

Kaiming He et al., "Deep Residual Learning for Image Recognition", CVPR2016

• 인풋 + 아웃풋 $\rarr x + F(x)$

• 인풋과 아웃풋이 모두 고려된 값이 Residual block 의 결과 값

• Residual Network 를 사용하는 이유

  • 기존에는 w 학습을 위해 Chain rule 을 활용했습니다.

  • w 가 너무 크면 최종 결과값 또한 엄청 커서 컴퓨터가 계산할 수 없는 값이 될 수 있습니다.

  • 따라서 노말 분포를 유지할 수 있도록 설정하여 w 가 너무 큰 값을 가지지 않게 합니다. (Xavier's initialization)

    • Xavier's Initialization

      • 각각의 output 이 노말 분포를 따르도록 하기 위해 웨이트 값을 어떤 분포의 값으로 초기화시켜야 되는지 제시하는 알고리즘

      • $W \sim \mathcal{N}(0, \sqrt{\frac{2}{\#(input) + \#(output)}})$

  • Chain rule 을 적용하면 w 업데이트를 위해서 w 값들의 곱이 활용되는데, 이때 w 초기값들이 0 근처에 있기 때문에 문제가 됩니다.

  • w 가 0 근처에 있고 w 값들을 곱하면 gradient 값이 0에 수렴하게 되어 업데이트가 되지 않는 현상이 발생합니다. (Gradient Vanishing)

  • 기존 수식

    • $\nabla_{\bold{w}_{l^0}^{t}}f_{CE}(\tilde{\bold{y}}, \bold{y}, \bold{x}) = \frac{\partial f_{CE}}{\partial \bold{w}_l^t} = \frac{\partial \bold{x}_l^t}{\partial \bold{w}_l^t} \times \prod_{l=l^0}^{L-2} \bold{w}_l \times \frac{\partial f_{CE}}{\partial \bold{x}_{L-1}^t}$

  • Residual Network 활용한 수식

    • $\nabla_{\bold{w}_{l^0}^{t}}f_{CE}(\tilde{\bold{y}}, \bold{y}, \bold{x}) = \frac{\partial f_{CE}}{\partial \bold{w}_l^t} = \frac{\partial \bold{x}_l^t}{\partial \bold{w}_l^t} \times \prod_{l=l^0}^{L-2} (\bold{w}_l + 1) \times \frac{\partial f_{CE}}{\partial \bold{x}_{L-1}^t}$

  • 이를 통해 기존 최대 30개 레이어만 활용 가능했던 것을 100~200개까지 활용 가능해졌습니다.

Class Activation Map (CAM)

"Learning Deep Features for Discriminative Localization", CVPR2016

• DNN 이 내부적으로 보이는 반응성을 기반으로 목표 클래스가 구체적으로 어디에 존재하는지 찾을 수 있는 알고리즘

• Convolution Layer: 필터의 반응성을 보여주는 맵 출력

• 최종 convolution filter 의 결과 값을 기반으로 현재 찾고자하는 클래스의 반응성을 추정해나가는 알고리즘

• 각각의 linear regressor 가 활용하고 있는 feature 하나가 한 개 convolution filter 의 반응성이 될 것

Probabilistic Deep Learning

• 확률적 모델에 기반한 딥러닝

• MC-DROPOUT

  • 랜덤하게 특정 웨이트를 0으로 만들어서 결과를 얻는 방법

  • 테스트할 때 적용하면 계속 결과값이 바뀌게 됨 -> 서로 다른 특징을 기반으로 예측이 된 결과 출력

  • 결과 값의 안정성을 기반으로 현재 DNN 이 예측하는 결과의 신뢰성을 결정

  • DNN 을 활용하여 결과 값의 안정성을 확인하고 싶다면 가장 쉬운 방법으로 적용 가능한 방법