[ML] 딥러닝의 깊이 있는 이해를 위한 머신러닝 3-1 (K-MOOC)

확률적 구분기(Naive Bayes)의 정의

Naive의 i는 영어가 아니라 다른 기호인데 비슷해서 일단 임시로 적어놨습니다.

확률적 구분기: 확률값을 기반으로 어떤 두 개의 물체를 구분하는 방법

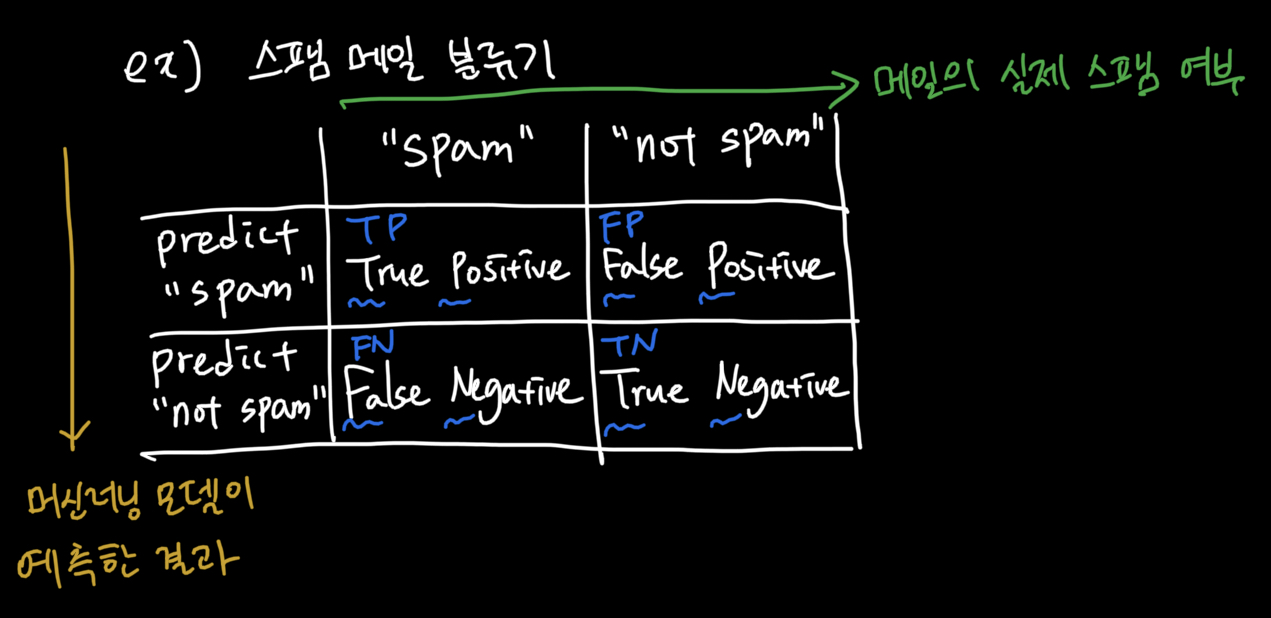
Precision & Recall

Precision: $\frac{TP}{TP+FP}$ 로 표현되며 스팸으로 예측된 모든 샘플들 중 맞는 것의 비율을 의미합니다.

Recall: $\frac{TP}{TP+FN}$ 로 표현되며 실제 스팸인 샘플등 중 맞는 것의 비율을 의미합니다.

• 놓치는 스팸이 발생한다? $\rarr$ FN 증가 $\rarr$ Recall 이 떨어집니다.

• Precision 과 Recall 은 반비례 관계에 있습니다. (다음 그림으로 설명 드리겠습니다. 제가 반비례 관계라는 것이 직관적으로 와닿지 않아서 따로 공부를 조금 더 해서 저만의 방식으로 설명 드립니다.)

• 위키피디아에서 제시하고 있는 예제를 그림으로 표현했습니다.

• 만약 Recall 값을 키우기 위해서 모든 사진을 강아지로 판별하면 어떻게 될까요?

• 위 그림처럼 Recall은 증가하지만 Precision은 감소하는 것을 볼 수 있습니다. 즉 Recall과 Precision은 하나가 커지면 다른 하나는 줄어드는 경향이 있음을 알 수 있습니다.

지도 학습 테스트 성능 측정은 어떻게 할까?

Precision-Recall Curve

x축: Recall

y축: Precision

ROC Curve

x축: False Positive Rate

y축: True Positive Rate

아래 면적이 넓을 수록 성능이 좋다.

F1 Score

Precision 과 Recall 의 조화 평균 값이며 식을 아래와 같습니다.

$F_1=(\frac{2}{recall^{-1}+precision^{-1}})$

Weighted F1 Score

여러 개의 클래스가 있을 때 활용

각 클래스로부터 얻은 F1 Score의 평균을 계산하여 활용합니다.

Random Variable

Random Variable: 확률에 의해 값이 결정되는 변수

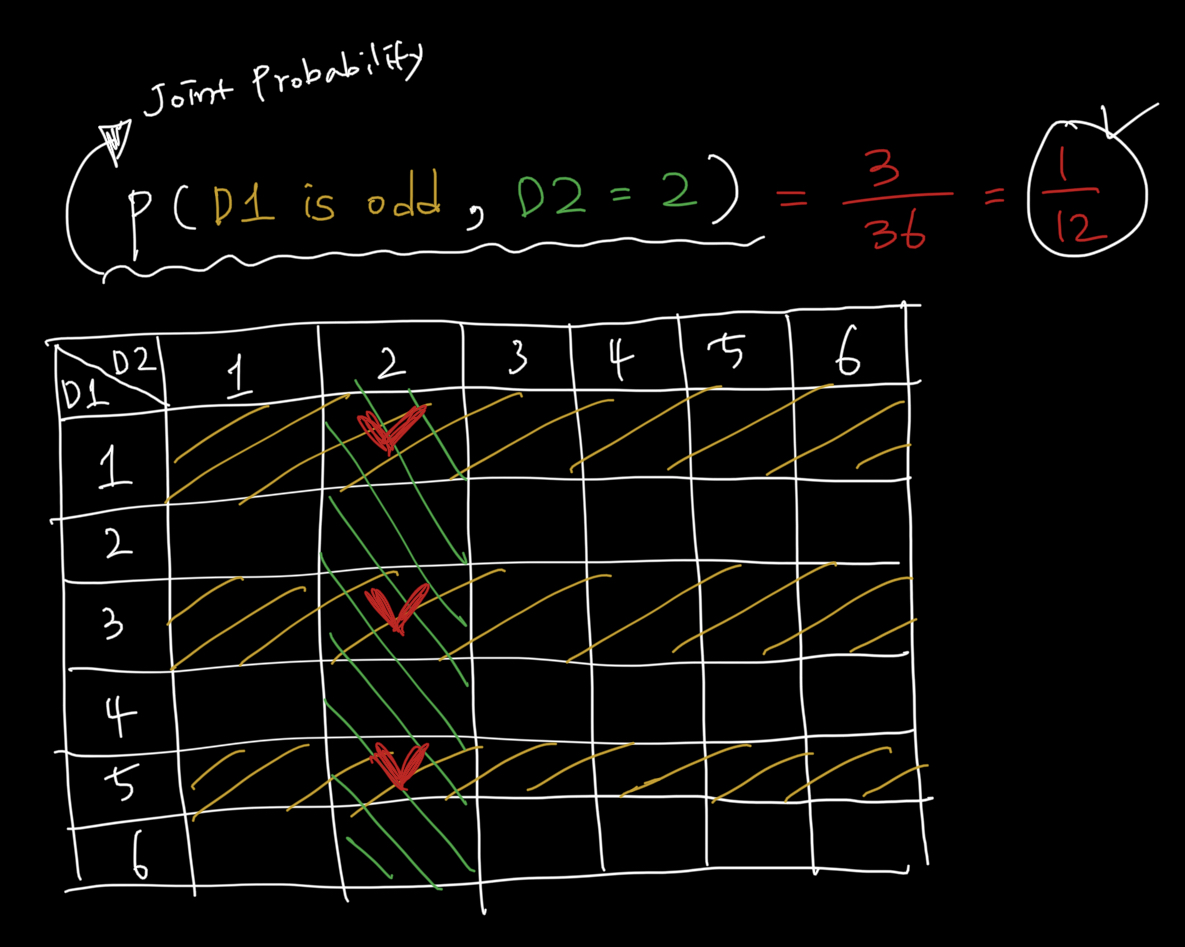
Joint Probability

두 개의 사건, 즉 두개의 Random variable이 동시에 발생하는 상황의 확률

$p(D_1 \text{ is odd}, D_2=2)$

두 개의 영역이 겹치는 부분에 대해서 확률 계산 (아래 그림을 보시면 이해가 더 잘 되실 겁니다.)

Marginalization Rule

어떤 A라는 이벤트가 발생할 확률과 A와 X가 모두 동시에 발생하는 확률의 관계

A와 X라는 사건이 동시에 발생하는 확률이 있다고 했을 때 X라는 이벤트가 발생할 수 있는 모든 케이스에 대해서 합 계산 (아래 식 참고)

• $p(A)=\sum_xp(A,X=x)$

• $\sum_x\sum_yp(X=x, Y=y)=\sum_xp(X=x)=1$

Conditional Probability

어떤 B라는 이벤트가 발생한 상황에 A라는 이벤트가 발생할 확률

• Joint Probability: A와 B라는 이벤트가 동시에 발생할 확률

• Conditional Probability: B 이벤트가 이미 발생한 상황에서 A 이벤트가 발생할 수 있는 확률

  • $p(A|B)$: a conditional probability of "A" given "B"

  • ex) 그림으로 대체합니다.

  

  • Product Rule: Joint Probability 와 Conditional Probability 의 관계를 표현 (아래 식을 참고하세요.)

    • $p(A|B)=\frac{p(A,B)}{p(B)}$

  • Bayes Rule: Product Rule 에서 조금 더 확장된 개념

    • $p(A|B)=\frac{p(A)\cdotp(B|A)}{p(B)}$ ($\because p(A,B)=p(A)\cdotp(B|A)$)

Independence of random variables

$p(A,B)=p(A)\cdotp(B)$

B가 일어나든지 말든지 A는 영향을 받지 않습니다.

Conditional independence

특정 조건 하에서 두 개의 랜던 variable 이 independent 한 것을 의미합니다. (아래 수식을 참고하세요.)

$p(A,B|C)=p(A|C)\cdotp(B|C)$

확률적 구분기란 무엇일까요...?

아래 그림으로 이해를 해봅시다.

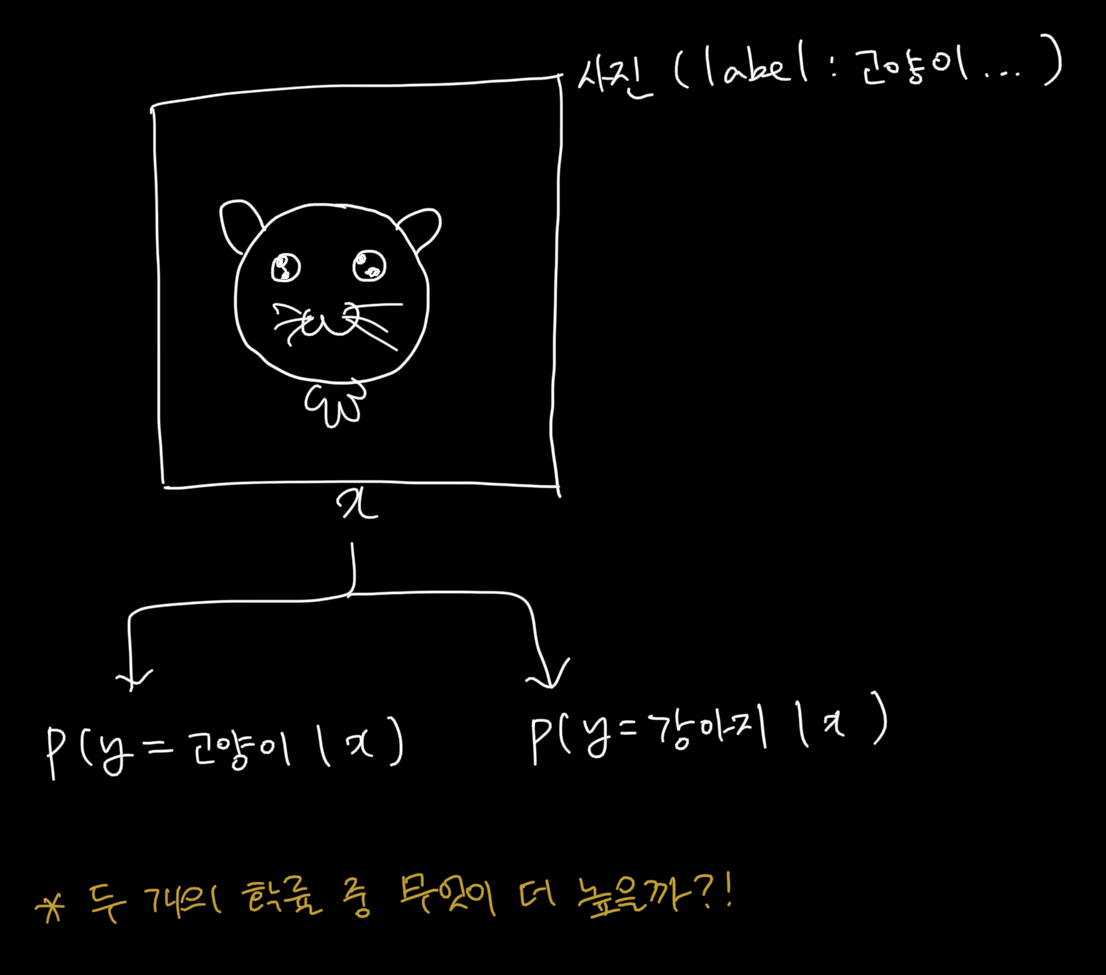
사진($x$)이 주어졌을 때, $p(y=cat|x)$ 와 $p(y=dog|x)$ 를 비교하여 사진이 무엇인지 결정하게 됩니다.