[ML] 딥러닝의 깊이 있는 이해를 위한 머신러닝 9-2 (K-MOOC)

학습내용

• Non-linear feature transform이란?

• Kernel Trick이란?

• Kernal Trick을 적용 시 효과

학습목표

• Non-linear Data를 머신러닝으로 학습할 수 있다.

• Non-linear Basis Function의 의미를 이해할 수 있다.

• Kernel Trick의 원리를 이해할 수 있다.

Non-linear Data 머신러닝 학습 방법

• 피쳐 엔지니어링

  • 현재 이미지나 데이터를 표현할 수 있는 피쳐 자체를 변형해서 다르게 추출하는 방법

• 커널트릭 (피쳐 트랜스폼)

  • 이미 추출된 피쳐를 한 번 더 변형해서 리니어 모델로 논리니어 데이터를 학습하는 방법

• 곡선(논리니어 형태)으로 표현하기 위해 피쳐의 변형이 필요!

• Non-linear feature transform의 정의

  • $\hat{y_i} = w_0 + w_1x_i + w_2x_i^2$

  • $\hat{y_i} = \vec{v}^T \vec{z_i} = v_1 z_{i1} + v_2 z_{i2} + v_3 z_{i3}$

  • 새로운 피쳐를 하나 조작 및 추가하여 선형 구조의 형태에서 비선형의 모델로 표현

• General Polynomial Features

  • P차 함수로 표현 가능한 데이터가 존재할 경우

  • $\vec{z} = \begin{bmatrix} 1 & x_1 & x_1^2 & \cdots & x_1^p \\ 1 & x_2 & x_2^2 & \cdots & x_2^p \\ \cdots & \cdots & \cdots & \cdots & \cdots \\ 1 & x_n & x_n^2 & \cdots & x_n^p \end{bmatrix}$

  • 논리니어 데이터는 위와 같이 표현 가능하지만 계산량이 기하급수적으로 증가한다...

  • 이를 해결하기 위해 kernel trick이 나타났습니다.

• kernel trick

  • 추가되는 모든 논리니어 텀을 위한 파라미터를 계산하지 않고, 그 중에 일부 계산만으로도 똑같은 결과나 효과를 얻을 수 있는 방법

  • Least Squares

    • $f(v) = \frac{1}{2}||\vec{z} \vec{v} - \vec{y}||^2 + \frac{1}{2}||\vec{v}||^2$

    • $\vec{z}$: kenel basis

    • $\vec{v}$: kernel weights

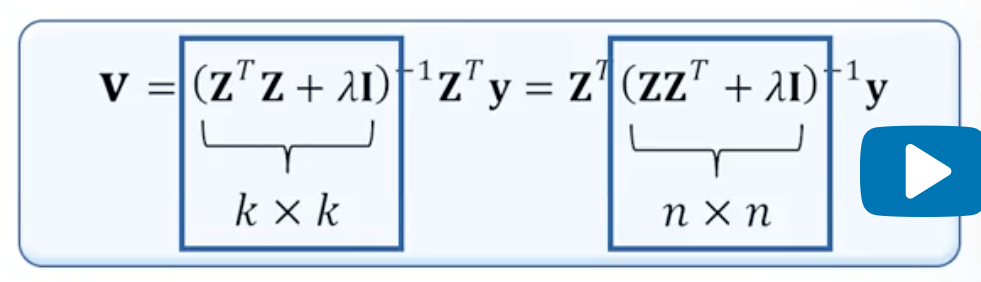
    • 기존의 $\vec{x}$보다 더 큰 매트릭스 값($\vec{z}$)을 얻고 normal equation 방법으로 $\vec{v}$ 값을 도출합니다.

    • 

    • normal equation에서 계산하는 방식과 동일합니다.

    • 계산량을 줄이기 위해 y앞에 곱해져 있는 z 트랜스 폼을 왼쪽으로 옮깁니다.

    • 매트릭스 인버스 계산은 연산량이 상당히 크기 때문에 실제 연산량 측면에서 큰 차이를 보입니다.

    • 여전히 고려하는 피쳐 디멘젼에 대해 어느 정도 비례하는 계산량을 보입니다.

    • 커널 트릭은 계산량을 한번 더 줄여나갑니다.

      • 

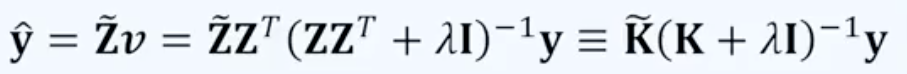
      • $\tilde{z}$의 새로운 프리딕션을 얻고자 할경우 학습된 $\vec{v}$를 $\tilde{z}$에 곱합니다.

      • $\vec{K}$의 경우 기존 학습된 피쳐 매트릭스의 형태를 갖춥니다.

      • $\vec{K}$ 연산을 바로 수행할 수 있다면 연산량을 크게 줄일 수 있습니다.

      • $\vec{z} \vec{z}^T$를 얻지 않아도 $\vec{K}$값을 구할 수 있는 커널 트릭 알고리즘...!

• 대표적인 커널 트릭 함수

  • 

  • $\vec{z}$를 사용하지 않아도 $\vec{K}$값을 계산할 수 있습니다!
    

  • Linear Kernel

    • k의 (i, j)에 해당되는 값은 i번째 샘플과 j번째 샘플 내적값 가집니다.

  • Polynomial Kernel

    • 다차항 함수의 경우 i번째 샘플과 j번째 샘플의 내적에 1을 더하고 전체 값의 p제곱 값을 계산하면 됩니다. (결국 다항식이 될 것입니다!)

  • Gaussian -RBF kernel은 설명을 생략합니다. (위에 그림에 나타난 수식 참조...!)

  • k의 값들을 샘플에서 곧바로 얻을 수 있기 때문에 굳이 아주 큰 크기의 z를 얻을 필요 없습니다.

  • 기존의 수많은 텀을 고려하는 것보다 훨씬 계산량을 줄일 수 있습니다.