Error Analysis for Iterative Methods

Order of Convergence

Definition 2.7

Suppose $\left\{p_n\right\}_{n=0}^{\infty}$ is a sequence that converges to $p$, with $p_n \neq p$ for all $n$. If positive constants $\lambda$ and $\alpha$ exist with

$\left\{p_n\right\}_{n=0}^{\infty}$가 모든 $n$에 대해 $p_n \neq p$인 $p$로 수렴되는 시퀀스라고 가정한다. 양의 상수 $\lambda$와 $\alpha$가 존재하는 경우

then $\left\{p_n\right\}_{n=0}^{\infty}$ converges to $p$ of order $\alpha$, with asymptotic error constant $\lambda$.

그런 다음 $\left\{p_n\right\}_{n=0}^{\infty}$는 점근 오류 상수 $\alpha$의 $p$로 수렴한다.

An iterative technique of the form $p_n=g\left(p_{n-1}\right)$ is said to be of order $\alpha$ if the sequence $\left\{p_n\right\}_{n=0}^{\infty}$ converges to the solution $p=g(p)$ of order $\alpha$.

$\left\{p_n\right\}_{n=0}^{\infty}$ 시퀀스가 $\alpha$ 차수의 솔루션 $p=g(p)$로 수렴하는 경우 $p_n=g\left(p_{n-1}\right)$ 형태의 반복 기술은 $\alpha$ 차수라고 한다.

Order $\alpha$

• In general, a sequence with a high order of convergence converges more rapidly than a sequence with a lower order.
• The asymptotic constant affects the speed of convergence but not to the extent of the order. Two cases of order are given special attention.
• Two cases of order are given special attention.
  (i) If $\alpha=1$ (and $\lambda<1$ ), the sequence is linearly convergent.
  (ii) If $\alpha=2$, the sequence is quadratically convergent.

일반적으로 수렴 순서가 높은 수열은 낮은 수열보다 빠르게 수렴한다.
점근 상수는 수렴 속도에 영향을 미치지만 차수의 범위까지는 영향을 미치지 않는다.
두 가지 order에 특별한 주의를 기울인다.
(i) $\alpha=1$(및 $\alpha<1$)이면 시퀀스는 선형 수렴한다.
(ii) $\alpha=2$이면 시퀀스는 2차적으로 수렴한다.

Illustration

Suppose that $\left\{p_n\right\}_{n=0}^{\infty}$ is linearly convergent to 0 with

and that $\left\{p_n\right\}_{n=0}^{\infty}$ is quadratically convergent to 0 with the same asymptotic error constant,

For simplicity we assume that for each $n$ we have

• For the linearly convergent scheme, this means that
  $\left|p_n-0\right|=\left|p_n\right| \approx 0.5\left|p_{n-1}\right| \approx(0.5)^2\left|p_{n-2}\right| \approx \cdots \approx(0.5)^n\left|p_0\right|,$
• whereas the quadratically convergent procedure has
  $\begin{aligned} \left|\tilde{p}_n-0\right|=\left|\tilde{p}_n\right| & \approx 0.5\left|\tilde{p}_{n-1}\right|^2 \approx 0.5\left[0.5\left|\tilde{p}_{n-2}\right|^2\right]^2=(0.5)^3\left|\tilde{p}_{n-2}\right|^4 \\ & \approx(0.5)^3\left[0.5\left|\tilde{p}_{n-3}\right|^2\right]^4=(0.5)^7\left|\tilde{p}_{n-3}\right|^8 \\ & \approx \cdots \approx(0.5)^{2^n-1}\left|\tilde{p}_0\right|^2 \end{aligned}$

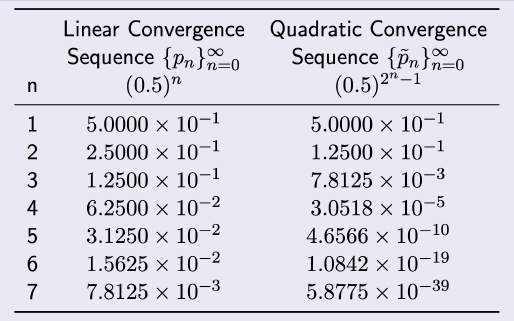
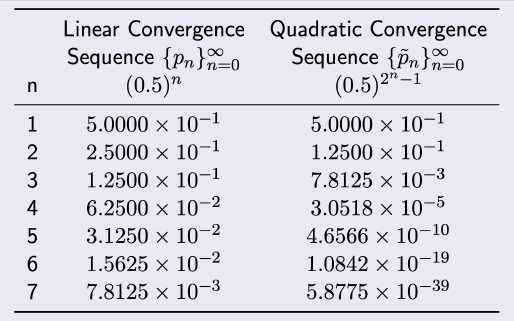
• The quadratically convergent sequence is within $10^{-38}$ of 0 by the seventh term. At least 126 terms are needed to ensure this accuracy for the linearly convergent sequence

  이차 수렴 시퀀스는 7번째 항까지 0의 $10^{-38}$ 내에 있다. 선형 수렴 시퀀스에 대한 이 정확도를 보장하기 위해 최소 126개의 항이 필요하다.

Theorem 2.8

Let $g \in C[a, b]$ be such that $g(x) \in[a, b]$, for all $x \in[a, b]$. Suppose, in addition, that $g^{\prime}$ is continuous on $(a, b)$ and a positive constant $k<1$ exists with

$g \in C[a, b]$가 모든 $x \in[a, b]$에 대해 $g(x) \in[a, b]$가 되도록 하자. 또한 $g^{\prime}$가 $(a, b)$에서 연속되고 양의 상수 $k<1$가 존재한다고 가정하자.

$\left|g^{\prime}(x)\right| \leq k, \quad$ for all $x \in(a, b)$.
If $g^{\prime}(p) \neq 0$, then for any number $p_0 \neq p$ in $[a, b]$, the sequence

converges only linearly to the unique fixed point $p$ in $[a, b]$.

$[a, b]$에서 고유한 고정점 $p$에만 선형적으로 수렴한다.

Theorem 2.9

Let $p$ be a solution of the equation $x=g(x)$. Suppose that $g^{\prime}(p)=0$ and $g^{\prime \prime}$ is continuous with $\left|g^{\prime \prime}(x)\right|<M$ on an open interval $I$ containing $p$. Then there exists a $\delta>0$ such that, for $p_0 \in[p-\delta, p+\delta]$, the sequence defined by $p_n=g\left(p_{n-1}\right)$, when $n \geq 1$, converges at least quadratically to $p$. Moreover, for sufficiently large values of $n$,

$p$를 $x=g(x)$ 방정식의 해라고 하자. $g^{\prime}(p)=0$ 및 $g^{\prime \prime}(x)$가 $p$를 포함하는 열린 간격 $I$에서 $|g^{\prime \prime}(x)|<M$와 연속된다고 가정한다.
그런 다음 $n \geq 1$일 때 $p_0 \in[p-\delta, p+\delta]$에 대해 $p_n=g\left(p_{n-1}\right)$에 의해 정의된 시퀀스가 적어도 $p$로 사분면적으로 수렴하는 $\delta>0$가 존재한다. 또한 $n$이 충분히 큰 값의 경우,