머신러닝 - 모델

강달봉·2023년 3월 19일

AIVLE kt sklearn 머신러닝 분류 에이블스쿨 회귀

머신러닝과 딥러닝

목록 보기

2/3

이미지출처
syntax 약속
본 포스팅은 KT 에이블스쿨 교육내용을 제 나름대로 정리하여 작성하였습니다

사이킷런에서는 다양한 회귀, 분류 알고리즘을 제공하고 있다. 하나하나 차근차근 알아보도록 하자.

선형 회귀(Linear Regression)

데이터의 회귀성
데이터들의 일련의 데이터 포인트들이 선형 패턴 또는 관계를 따르는 현상을 의미한다.
최적의 회귀모델이란?
전체 데이터의 오차합이 최소가 되는 모델
다중회귀와 단순회귀
독립변수 x 의 갯수로 나눌 수 있다. x가 하나면 단순, 여러개면 다중회귀 이다.
선형회귀식
선형회귀는 최선(최소 오차)의 가중치와 편향을 찾는 과정이라고도 할 수 있다.
$\hat{y} = w_0 + w_1 x_1 + w_2 x_2 \, ... \, w_n x_n$ $w_0 = 가중치$ $w_1,\, w_2,\, w_n = 편향$

model.coef_ 로 변수(feature) 별 편향을 알 수 있으며,
model.intercept_ 로 가중치를 알 수 있다.

K 최근접 이웃(K - Nearest Neighbor)

'K' 개의 근처값으로 값을 추측하는 지도학습 알고리즘이다.
회귀와 분류 둘 다 사용된다. 판단기준은 회귀에서는 k 개의 값의 평균이며, 분류에서는 가장 많이 포함된 유형(class)이다.

K 값
적절한 값을 찾는게 중요한 머신러닝에서, K값도 물론 적절하게 찾아줘야한다.
K 값을 1로 설정하면 너무 편향된 값을 얻으며, K = 6 처럼 값이 짝수이면 과반수를 구할 수 없는 문제점들이 있다.
거리
근처, 즉 가장 가까운 거리에 있는 값들은 어떻게 판단할까?
- 유클리드(Euclidean) 방법
  두 점 간의 유클리드 거리를 구하는 방법이라고는 하는데... 쉽게 말하자면 피타고라스 법칙을 이용해서 거리를 구하는 법이라고 이해하면 편하다.(두 점사이의 완전 직선 거리)
- 맨하탄(Manhattan) 방법
  맨하탄( = 잘 계획된 격자형식의 도시)에서 길을 찾는 방법을 연상하면 된다. 직각 좌표의 좌표값 차이로 거리를 구한다.
스케일링
KNN 방식은 모든 데이터가 같은 값의 범위를 구할 때 가장 좋은 성능을 보여주기 때문에 스케일링이 필수적이다. 링크의 정규화를 참고하자.

결정 트리(Decision Tree)

특정 변수에 대한 의사결정 규칙을 나뭇가지가 뻗는 형태로 분류한 알고리즘이다.
분류와 회귀 모두 사용된다.
직관적, 쉬운 설명과 이해, 스케일링이 불필요하다는 장점이 있으며
의미있는 질문을 하지 못하면 학습성능이 좋지 못하다는 것과 과적합으로 인한 모델 성능 감소 가능성이 높다는 단점이 있다.
결과적으로 분할이 많이 될 수록 과적합 위험이 높아지는 방식이므로, 하이퍼파라미터들을 이용해 분할을 제한한다.(like 가지치기)
백문이 불여일견이라고 시각화된 트리를 보면서 이야기해 보자.

코드

import numpy as np
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier, plot_tree
import matplotlib.pyplot as plt
%config InlineBackend.figure_format = 'retina'
# Load the iris dataset
iris = load_iris()
X = iris.data
y = iris.target

# Split the dataset into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Initialize the Decision Tree Classifier
clf = DecisionTreeClassifier(random_state=42)

# Fit the classifier to the training data
clf.fit(X_train, y_train)

# Visualize the decision tree
plt.figure(figsize=(12, 8))
plot_tree(clf, feature_names=iris.feature_names, class_names=iris.target_names, filled=True)
plt.show()

결과
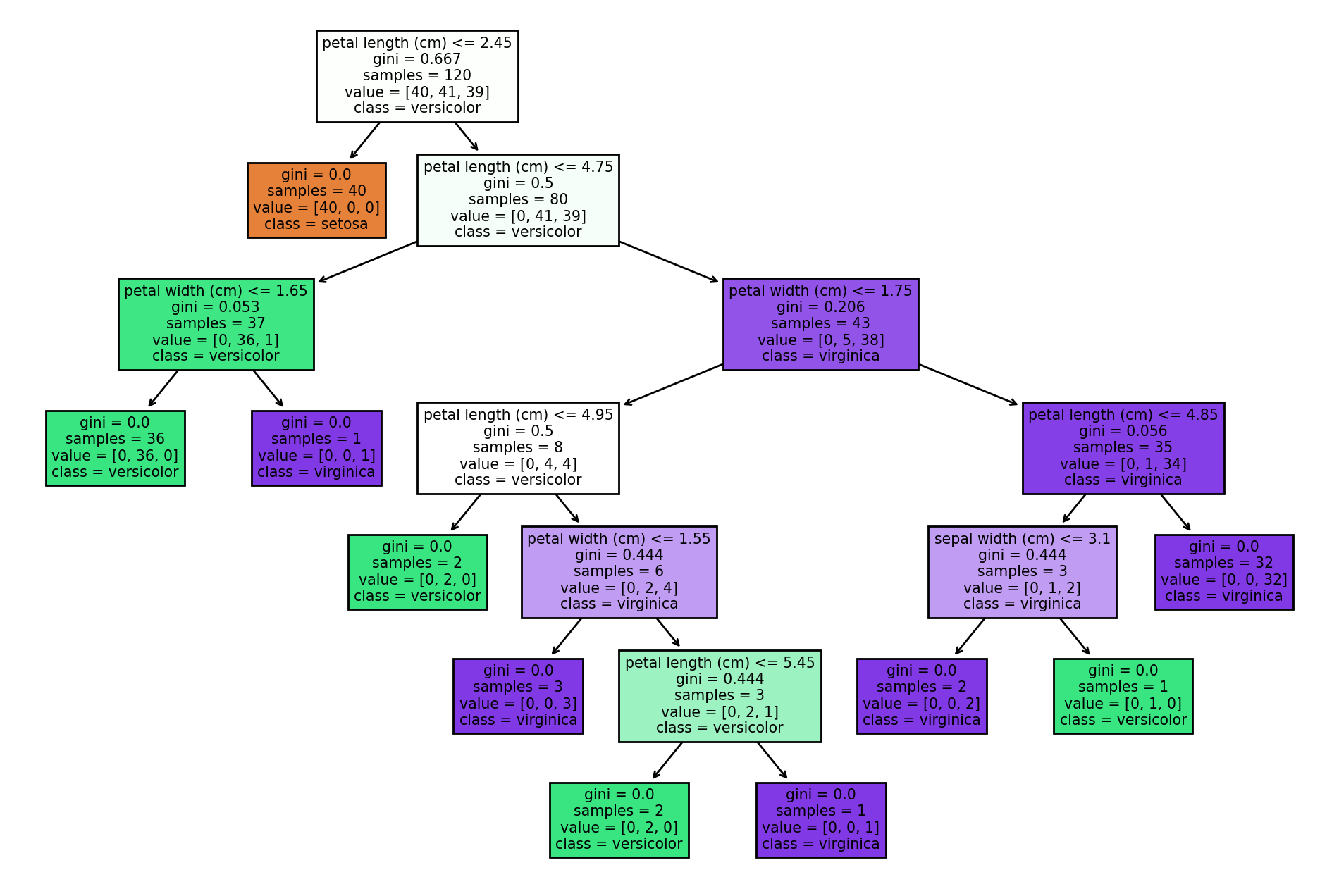시각화 사진에서 네모 하나를 '노드' 라고 부르는데, 노드에는 각각의 정보가 담겨 있다.

분할 조건 또는 규칙: 데이터를 분할하는 데 사용되는 기능의 경계값.
지니 불순도: 각 노드에 대한 불순도 또는 오분류 정도.
샘플 수: 노드에 도달한 총 샘플 수로 노드의 대표성을 추정하는 데 사용.
값 배열: 노드의 각 클래스에 대한 샘플 분포.
예측 클래스: 노드에서 샘플의 비율이 가장 높은 클래스.

지니 불순도?

Decision Tree에서 불순도(얼마나 섞여있는지)를 측정하기 위한 지표이다.
불순도를 통해서 값이 얼마나 분류가 잘 되었는지를 추론할 수 있다.
값은 0 ~ 0.5 까지 이며, 0에 가까울 수록 분류된 데이터의 순도가 높다고 할 수 있으며, 이는 곧 분류가 잘 되었음을 의미한다. 지니 불순도의 값이 낮을걸로 Decision Tree의 노드를 결정한다.

Gini = 1 - \sum (p_i)^2

= 1-(양성class비율^2 + 음성class비율^2)

지니 불순도 높을수록 -> 분류잘안됨(안좋음) 만 기억하자

엔트로피와 정보이득

엔트로피
지니계수와 같이 데이터의 불순도를 확인할 수 있는 지표이다.
값은 0 ~ 1 까지 이며, 값의 의미는 지니 불순도와 같다
$Entropy = -\sum_{i=1}^{n} p_i \log_2 p_i$ $= -(음성class비율)\times\log_2 (음성clas비율) - (양성class비율)\times\log_2 (양성clas비율)$ $p_i : 집합 안에서 \, i 의 \, 확률$
정보이득
엔트로피를 이용해 구할 수 있다. 어떤 속성이 얼마나 많은 정보를 제공하는지를 알 수 있다.
부모 노드와 자식 노드의 엔트로피 '차이'의 가중평균으로 계산한다.
$InformationGain = Entropy(parent) - \sum_{i=1}^{k} \frac{|D_i|}{|D|} Entropy(D_i)$

정보이득은 으로 노드를 나누게 되면 엔트로피를 더 많이 감소시킬 수 있는 방식으로 값을 나누기 때문에, 뚜렷한 값이나 범주를 가진 변수에 편향될 수 있다는 점이 있다. 그러므로 변수가 많을 때에는 지니계수를 쓰는게 좋다.

하이퍼파라미터	설명	사용 예시
`max_depth`	트리의 최대 깊이. 트리 성장을 제한하여 과적합을 방지합니다.	`max_depth=10`
`min_samples_split`	내부 노드를 분할하는 데 필요한 최소 샘플 수. 작은 노드로 인한 과적합을 방지합니다.	`min_samples_split=20`
`min_samples_leaf`	리프 노드에 있어야 하는 최소 샘플 수. 리프의 크기를 조절합니다.	`min_samples_leaf=5`
`max_features`	최적의 분할을 찾을 때 고려할 기능 수의 최대값. 무작위성을 증가시켜 과적합을 방지할 수 있습니다.	`max_features="sqrt"`
`max_leaf_nodes`	최대 리프 노드 수. 과적합을 방지하기 위해 리프 노드 수를 제한합니다.	`max_leaf_nodes=50`
`min_impurity_decrease`	노드 분할에 필요한 최소 불순도 감소. 이 값보다 작은 불순도 감소는 분할을 하지 않습니다.	`min_impurity_decrease=0.01`
`min_impurity_split`	분할을 중단할 불순도의 임계값. 이 값을 초과하는 불순도를 가진 노드는 분할을 중단합니다. (deprecated)	`min_impurity_split=0.1` (사용되지 않음)
`criterion`	분할을 결정하는 기준. "gini"(지니 불순도) 또는 "entropy"(엔트로피) 중 하나를 선택할 수 있습니다.	`criterion="gini"`
`splitter`	각 노드에서 분할을 선택하는 전략. "best"는 최적의 분할을 선택하고, "random"은 무작위 분할을 선택합니다.	`splitter="best"`

작성하기 귀찮아서 gpt한테 맡김 ㅋㅋ

로지스틱 회귀(Logistic Regression)

종속변수의 결과값이 이분법으로 나누어 지는 경우(이진결과)에 사용된다.(예 아니오, 참 거짓, 0 1)
선형 회귀선을 찾는것이 아니고 로지스틱(시그모이드) 함수에 반환되는 값을 확률로 간주하여 값 0.5를 기준으로 이진 분류를 수행한다.

회귀라는 이름은 갖지만 선을 찾는건 아니고, 정해져 있는 선에 값을 찍어서 확률값을 통해 0, 1 을 분류한다는 소리인 것 같다.
쉽게 풀어쓴답시고 썼는데 위에문장이랑 별 차이 없는것같다.

Support Vector Machine

분류를 위한 기준선(결정경계선)을 찾는 알고리즘. 의외로 분류와 회귀 둘 다 사용할 수 있다.
각각 SVC(Support Vector Classification), SVR(Support Vector Regression) 으로 불린다.
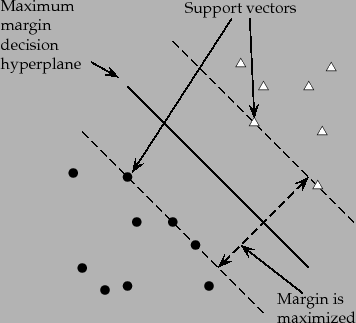
마진을 '최대'로 하는 결정 경계를 찾는것이 SVM의 목표이다.
성능을 높이기 위해서 정규화(scaling)가 필수이다.

서포트 벡터(Support Vector)
결정 경계선과 가장 가까운 데이터 포인트
마진(margin)
결정경계선과 서포트 벡터 사이의 거리
Cost(정규화 매개변수)
분류 오류를 결정하는 값, 마진을 최대화 할 수 있다. 값을 높일수록 더 넓은 마진을 허용하지만 오분류가능성이 있다. 누누히말하지만 적절한 Cost 값을 찾는게 중요하다.
높으면 과대적합, 낮으면 과소적합 위험이 있다.
초평면(Hyperplane)
SVM의 결정 경계를 의미한다. 데이터가 나타나는 공간보다 차원이 하나 적다. 그래서 2차원에서는 경계선(1차원), 3차원에서는 경계면(2차원) 이 된다.
커널 함수(Kernel function)
대부분의 데이터는 선형으로 분류하기 힘드므로 커널 함수를 이용하여 비선형으로 데이터를 분류한다. 데이터간에 다른차원으로 분리해서 분류를 한다나 뭐라나...
RBF(Radial Basis Function)이 가장 많이 쓰인다.
감마(gamma)
비선형 SVM에서 쓰이는 값으로, 모델이 생성하는 경계가 복잡해지는 정도를 나타낸다.
Cost와 비슷한 역할을 한다고 생각하면 될 것 같다.

기본 알고리즘 데이터 전처리 정리

알고리즘	스케일링	범주형 변수 처리
선형 회귀	필요 없음	가변수화
KNN	필요	가변수화
의사결정나무	필요 없음	필요 없음
로지스틱 회귀	필요 없음	가변수화
SVM	필요	가변수화

앙상블 알고리즘

여러가지 기본 모델 알고리즘들을 결합하여 하나의 최종 예측 모델을 생성하는 방법.
일반적으로 단일 모델보다 다 나은 성능과 과적합이 줄어든다.

보팅(Voting)

여러개의 알고리즘이 투표를 통해 최종 예측 결과를 결정하는 방식, 소프트보팅과 하드보팅이 있다.
분류로 예시를들어 차이를 설명하자면 다음과 같다.

하드 보팅
다수의 알고리즘이 예측한 클래스 값이 최종 결과값
소프트 보팅
모든 알고리즘이 예측한 클래스 값의 확률의 평균을 귀한뒤 가장 높은 값을 가진 클래스를 최종 결과로 선정

예시 코드 분류인지 회귀인지에 따라 Voting 뒤에 오는 글자를 다르게 하면 된다.

import numpy as np
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.ensemble import VotingClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier
from sklearn.neighbors import KNeighborsClassifier

# Load the iris dataset
data = load_iris()
X, y = data.data, data.target

# Split the data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Define the base models
lr = LogisticRegression()
dt = DecisionTreeClassifier()
knn = KNeighborsClassifier()

# Create the Voting Classifier using the base models
voting_classifier = VotingClassifier(estimators=[('lr', lr), ('dt', dt), ('knn', knn)], voting='hard')

# Train the Voting Classifier on the training data
voting_classifier.fit(X_train, y_train)

# Make predictions on the test data
y_pred = voting_classifier.predict(X_test)

# Calculate the accuracy of the Voting Classifier
accuracy = accuracy_score(y_test, y_pred)
print(f"Voting Classifier Accuracy: {accuracy:.2f}")

배깅(Bagging)

'Bootstrap Aggregating' 약자, 데이터로부터 부트스트랩(샘플링의 한 종류) 한 데이터로 모델을 학습시킨 후, 학습된 모델의 결과를 집계하여 최종 결과를 얻는 방법. 분산을 줄이고 과적합을 방지하는데 도움이 된다.
다수의 모델을 예측 후 결합을 하는 방식에서 샘플링과 비슷한 측면이 있지만, 같은 모델로 학습을 한다는 점(랜덤 포레스트)과, 샘플링된 데이터를 사용한다는 차이가 있다.

랜덤 포레스트(Random Forest)

배깅을 이용한 앙상블의 가장 대표적인 알고리즘, Decision Tree 알고리즘을 여러 번 사용하여 결합한다는 의미에서 Forest라는 의미가 붙었다.
두가지를 무작위로 선택한다. 한가지는 배깅 알고리즘이라는 점에서 추측할 수 있듯이, 데이터를 부트스트래핑한다는 것이고, 나머지 하나는 Decision Tree의 분할 기준이 되는 Feature를 랜덤으로 선택하는 것이다.

주요 하이퍼파라미터는 Decision Tree 와 비슷하다.

하이퍼파라미터	설명
`n_estimators`	숲에 있는 나무의 수. 나무의 수를 늘리면 일반적으로 모델 성능이 향상되지만 계산 시간이 늘어난다.
`max_features`	각 노드에서 분할을 위해 고려되는 특성의 최대 개수. 이 값을 줄이면 다양성이 증가하여 과적합을 줄일 수 있다.
`max_depth`	나무의 최대 깊이. 이 값을 제한하면 모델의 복잡성이 감소하여 과적합을 방지할 수 있다.
`min_samples_split`	노드를 분할하기 위한 최소 샘플 수. 이 값을 높이면 모델의 복잡성이 감소하여 과적합을 방지할 수 있다.
`min_samples_leaf`	리프 노드에 필요한 최소 샘플 수. 이 값을 높이면 모델의 복잡성이 감소하여 과적합을 방지할 수 있다.

부스팅(Boosting)

같은 유형의 알고리즘 기반 분류기 여러 개에 대해 순차적으로 학습을 수행하는 알고리즘.
Decision Tree를 병렬적으로 훈련하는 Random Forest와 달리, 순차적으로 훈련한다는 차이가 있다. 즉, 이전 분류기 학습 결과에 영향을 받는다.
배깅에 비해 성능이 좋지만 속도가 느리고 과적합 가능성이 있다.
이러한 부스팅 알고리즘을 최적화하고 효율화하여 개선한 XGBoost 알고리즘이 자주 사용된다.
다음은 XGBoost 알고리즘의 하이퍼파라미터이다.

하이퍼파라미터	설명	일반적인 값과 기본값
`learning_rate`	학습률입니다. 각 부스팅 단계에서 새로운 weak learner의 가중치를 조정하는 데 사용됩니다. 일반적으로 낮은 값이 설정됩니다.	일반적인 값: 0.01 ~ 0.3, 기본값: 0.3
`max_depth`	각 weak learner(결정 트리)의 최대 깊이입니다. 이 값을 줄이면 과적합을 방지할 수 있습니다.	일반적인 값: 3 ~ 10, 기본값: 6
`min_child_weight`	자식 노드에 필요한 최소 가중치 합입니다. 이 값을 높이면 과적합을 방지할 수 있습니다.	일반적인 값: 1 ~ 20, 기본값: 1
`gamma`	트리 분할을 허용하는 데 필요한 최소 손실 감소입니다. 이 값을 높이면 과적합을 방지할 수 있습니다.	일반적인 값: 0 ~ 20, 기본값: 0
`subsample`	각 weak learner를 학습하는 데 사용되는 샘플의 비율입니다. 이 값을 낮추면 과적합을 방지할 수 있습니다.	일반적인 값: 0.5 ~ 1, 기본값: 1
`colsample_bytree`	각 weak learner를 학습하는 데 사용되는 특성의 비율입니다. 이 값을 낮추면 과적합을 방지할 수 있습니다.	일반적인 값: 0.5 ~ 1, 기본값: 1
`lambda`	L2 정규화 항의 가중치입니다. 이 값을 높이면 과적합을 방지할 수 있습니다.	일반적인 값: 0 ~ 10, 기본값: 1
`alpha`	L1 정규화 항의 가중치입니다. 이 값을 높이면 과적합을 방지할 수 있습니다.	일반적인 값: 0 ~ 10, 기본값: 0
`n_estimators`	부스팅 단계(weak learner)의 수입니다. 더 많은 단계가 진행될수록 모델이 복잡해지지만 과적합이 발생할 수 있습니다.	일반적인 값: 100 ~ 1000, 기본값 100

catboost?

최근에 나온 그라디언트 부스팅 알고리즘이다.
범주형 특성에 효율적으로 처리하도록 설계되었으며 GPU 가속을 이용할 수 있어서 다른 그라디언트 부스팅 알고리즘보다 더 빠르다고 한다.
알고리즘의 기술적인 특징에 관련해서 아주 잘 요약한 블로그 글이 있어서 따로 포스팅은 생략...

스테킹(Stacking)

여러 모델의 예측 값을 최종 모델의 학습 데이터로 사용하여 예측하는 방법.
기본모델과 최종모델로 나누어서 학습을 진행한다. 여러개의 기본모델로 학습을 진행한 뒤 마지막으로 최종모델을 이용하여 최종 예측을 수행하는 알고리즘이다.
도식화

      Base Model 1   Base Model 2   ...   Base Model N
          |              |                      |
          v              v                      v
        ┌─────┐        ┌─────┐                ┌─────┐
Training┤  M1 ├────────┤  M2 ├────────────────┤  MN ├─────┐
 Data   └─────┘        └─────┘                └─────┘     |
           |              |                      |        |
           v              v                      v        v
        ┌─────┐        ┌─────┐                ┌─────┐   ┌─────┐
 Test   ┤  M1 ├────────┤  M2 ├────────────────┤  MN ├───┤MetaM├─── Final Prediction
 Data   └─────┘        └─────┘                └─────┘   └─────┘
           |              |                      |
           v              v                      v
      Predictions 1  Predictions 2          Predictions N

예시 코드

import numpy as np
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.ensemble import StackingClassifier

# Load Iris dataset
data = load_iris()
X, y = data.data, data.target

# Split the dataset into training and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Define base models
base_models = [
    ('logistic_regression', LogisticRegression()),
    ('knn', KNeighborsClassifier(n_neighbors=3)),
    ('random_forest', RandomForestClassifier(n_estimators=100, random_state=42))
]

# Define the meta-model
meta_model = LogisticRegression()

# Create the stacking classifier
stacking_classifier = StackingClassifier(estimators=base_models, final_estimator=meta_model)

# Fit the stacking classifier to the training data
stacking_classifier.fit(X_train, y_train)

# Evaluate the stacking classifier on the test data
score = stacking_classifier.score(X_test, y_test)
print(f"Stacking Classifier Test Accuracy: {score:.2f}")