- 문제 정의와 해결 방안

선형관계: A, B가 있을 때, A가 증가하면 B가 증가하거나, A가 증가하면 B가 감소하는, 서로 일관되게 변화량이 연관되어있을 때 선형적인 관계라고 일단 단순하게는 그렇게 생각하면 된다.
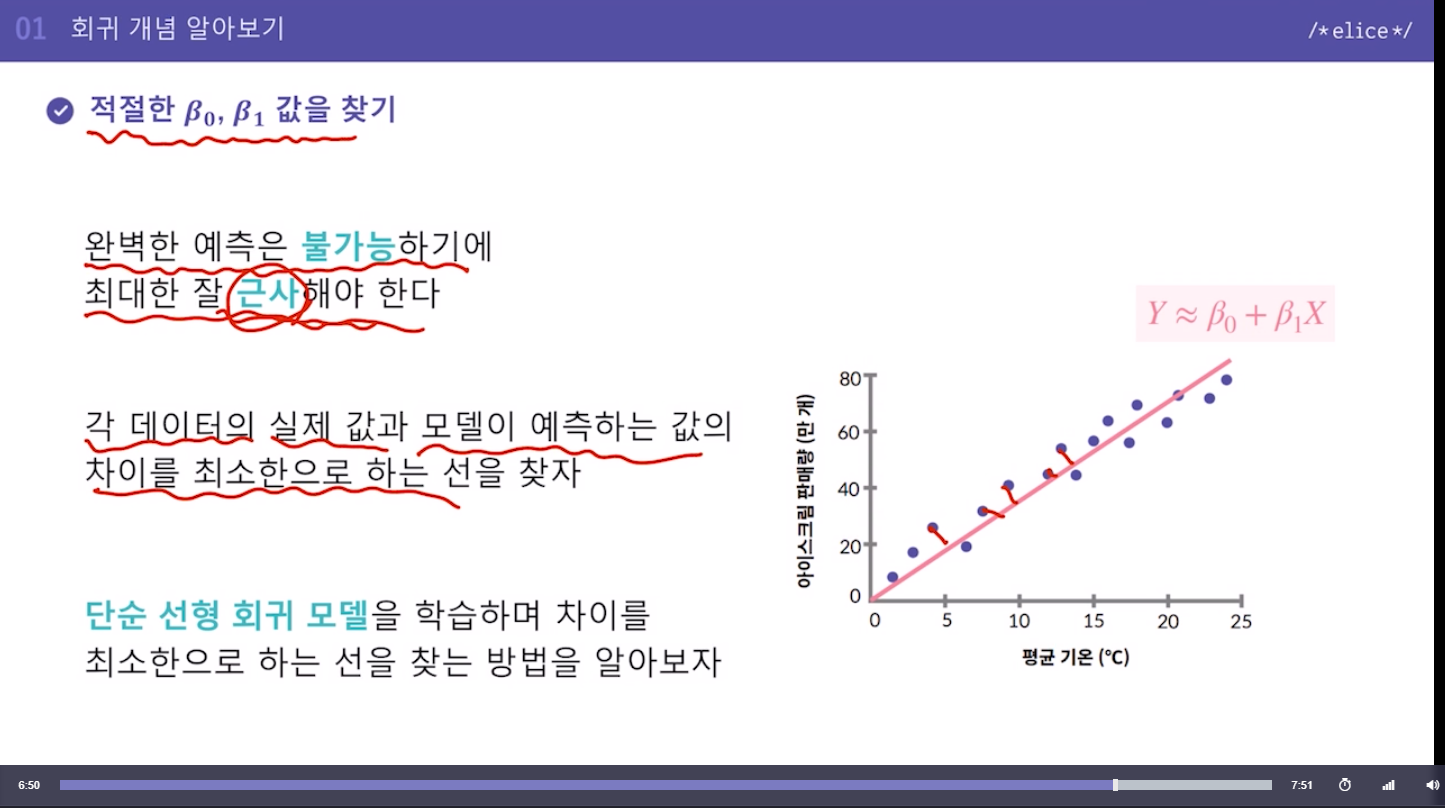
평균기온에 따른 아이스크림 판매량
-> 지도학습 -> 판매량이 레이블, 피쳐데이터는 평균기온.
- 회귀분석이란?
Label 데이터가 수치형 데이터일 때.
선을 찾는다 = 베타0와 베타1을 찾는 것.
X와 Y는 우리가 갖고 있는 데이터, 베타0, 베타1을 근사해서 찾아내는 것이 목표.
- 단순 선형 회귀
데이터를 설명하는 모델을 '직선 형태'로 가정
가정 Y ~~ B0 + B1 * X
직선을 구성하는 B0 (y절편)과 B1(기울기)를 구해야함
- 데이터를 잘 설명한다는 것은 어떤 것일까?
실제 정답과 내가 예측한 값과의 차이가 작을수록 좋지 않을까?
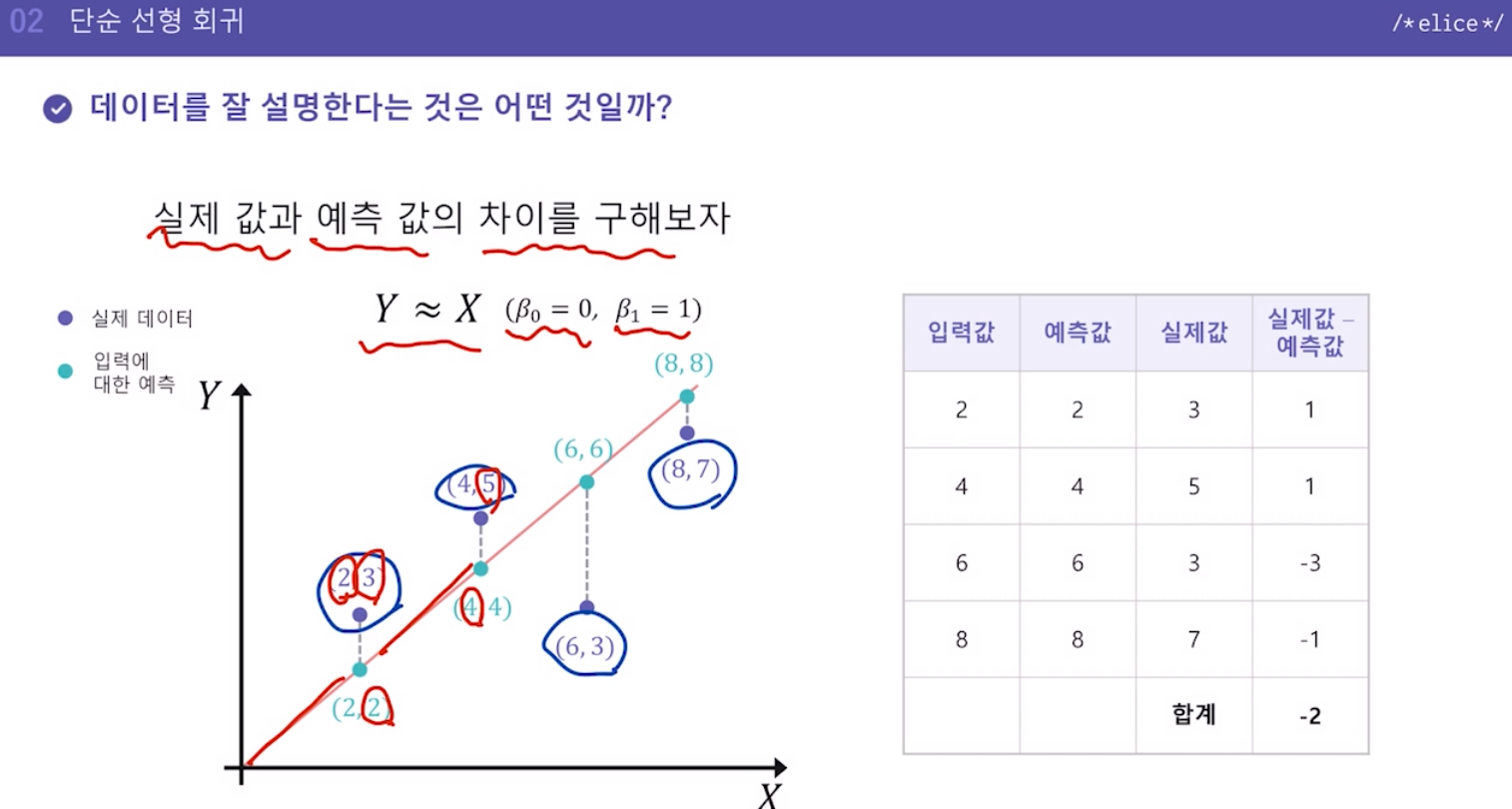
- 실제값과 예측값의 차이를 그냥 더했을 때 문제를 해결하기 위해
실제값과 예측값 '차이의 제곱의 합'으로 비교 -> 이게 작을수록 예측이 잘된 것.
이것을 "Loss함수"로 정의.
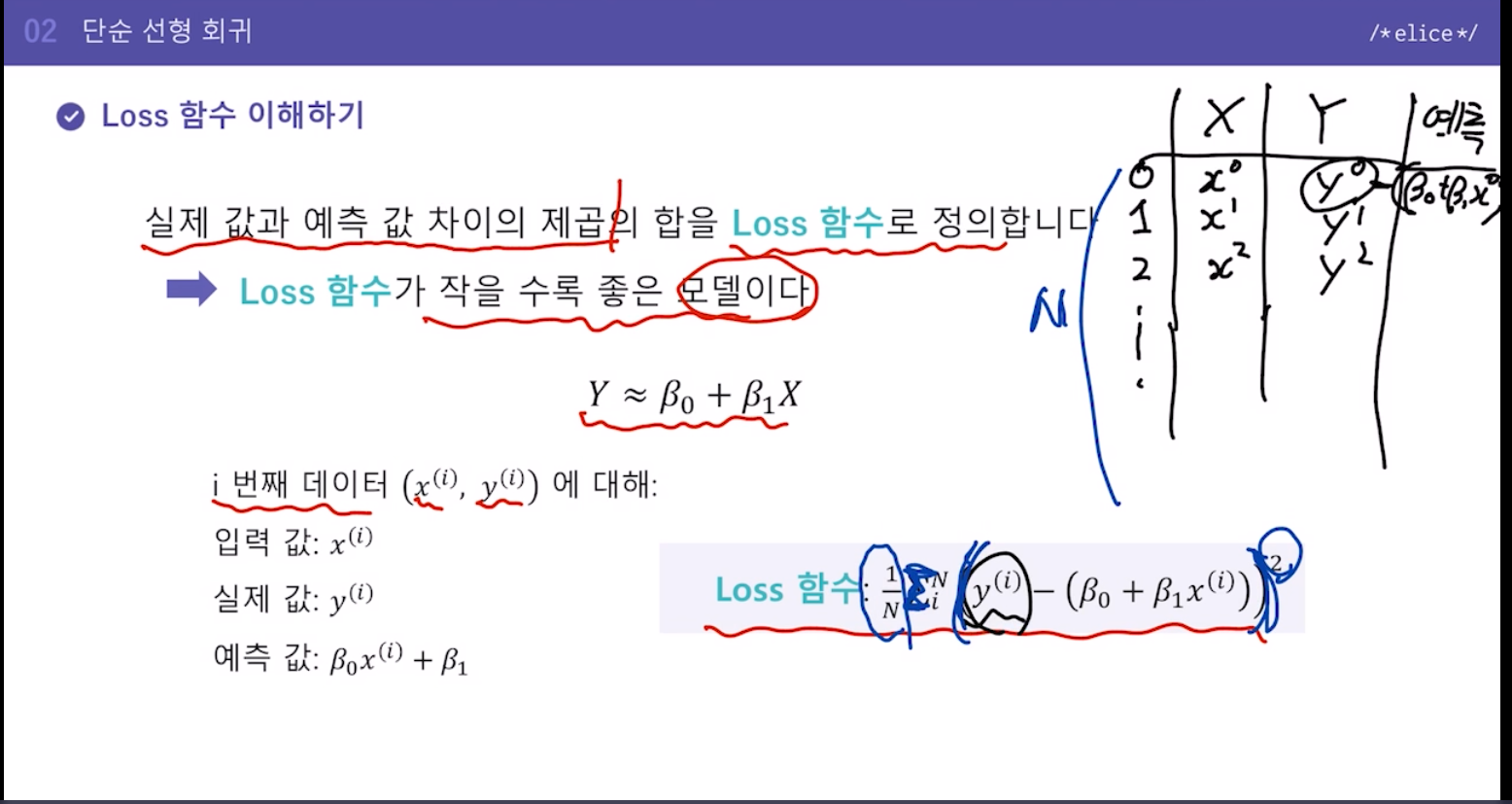
마지막엔 1/N 으로 나눠 평균을 냄.
-
Loss함수에서 주어진 값은 입력 값과 실제 값이다.
y절편과 기울기값을 조절하여 Loss함수 크기를 작게 한다. -

argmin 이란, 최소값을 찾는 건데 파랗게 표시된 B0, B1 값을 조절하여 Loss함수의 최소가 되게 하는 B0, B1값을 찾는다는 의미
크게 두가지 방식. 1), 2)
경사하강법은 딥러닝에도 많이 쓰이는 중요한 개념.
Normal equation 은 수학적으로 상당히 어려워서 이번 강의에선 스킵
- 경사하강법
Loss함수값이 제일 작게 하는 y절편, 기울기를 B0, B1 이라고 하면 계산 한번으로 구하는 것이 아니라 초기값에서 점진적으로 구하는 방식
초기값을 업데이트해가면서 최적의 값을 찾아가는 방식
1) y절편과 기울기값을 랜덤하게 초기화
2) 현재 값으로 Loss값 계산
3) y절편, 기울기값을 어떻게 변화해야 Loss값을 줄일 수 있는지 알 수 있는 'Gradient값' 계산 (이 gradient값을 어떻게 구하는지는 아직 얘기하지 않을 것)
4) Gradient 값을 활용하여 y절편, 기울기값 업데이트
5) Loss 값의 차이가 거의 없어질 때까지 2~4번 과정을 반복(Gradient값도 계속 다시 구하는 것)(Loss 값과 차이가 줄어들면 Gradient 값도 작아짐)

완벽히 맞힐 수도 있고 아닐 수도 있지만 거의 근접한 값을 구하게 됨.
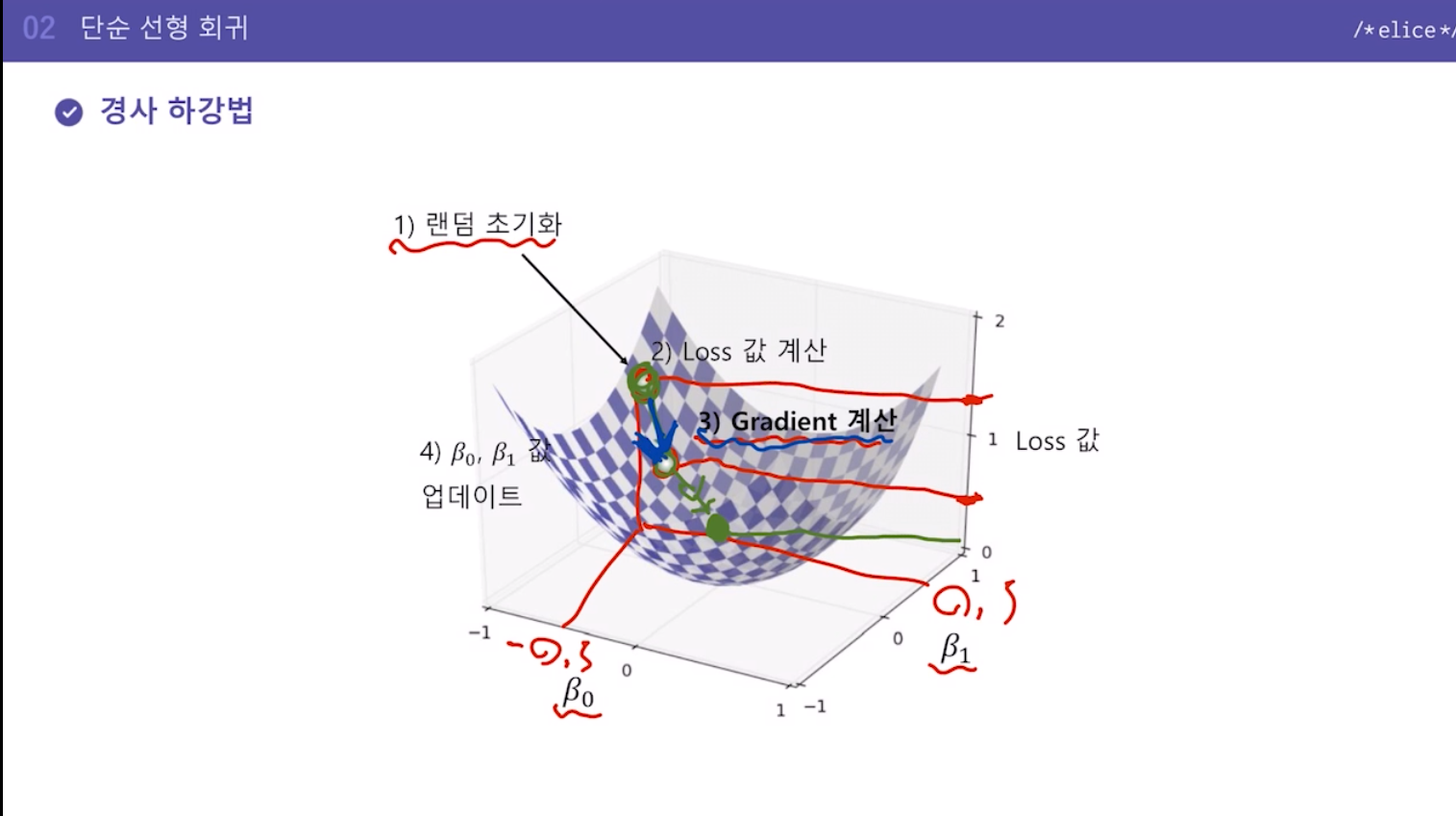
이 경사가 Gradient, 경사를 따라 내려감.
Gradient값을 구하려면 편미분, 자세히 설명하지 않음.
- 단순 선형회귀 특징
- 가장 기초적이나 여전히 많이 사용되는 알고리즘
- 입력값이 1개인 경우에만 적용이 가능함 ( 평균기온(1개) -> 아이스크림 판매량 )
- 입력값과 결과값의 관계를 알아보는 데 용이함
- 입력값이 결과값에 얼마나 영향을 미치는지 알 수 있음 -> 기울기값에 따라 관계를 얼마나 크게 미치는지 알 수 있음(x가 조금만 증가해도 y가 크게 증가하는 등)
- 두 변수 간의 관계를 직관적으로 해석하고자 하는 경우 활용
