[ADsP] 통계 분석

당당·2023년 7월 19일

ADsP 통계 분석

ADsP

목록 보기

10/13

📔설명

통계의 정의와 자료 획득 방법을 알아보고, 통계분석과 통계분석 방법을 알아보자.
확률 및 확률분포를 알고, 추정과 가절검정을 알아보자.

통계

간단한 테이블 또는 그래프에서 아주 복잡한 분석 결과까지 형태는 다양

통계자료 획득 방법

총조사
샘플링 조사

통계분석의 방법

기술통계
통계적 추론

추정

표본으로부터 모집단이 가지는 특성(모수)를 추측하는 것

가설검정

자신이 가진 이론적 대안이 통계적으로 의미가 있는지를 확인하는 것

🏓통계분석의 이해

통계

특정집단을 대상으로 수행한 조사나 실험을 통해 나온 결과에 대한 요약된 형태
ex) 일기예보, 물가/실업률/GNP, 의식조사와 사회조사 분석 통계, 임상실험 통계
조사 또는 실험을 통해 데이터 확보, 조사 대상에 따라 총조사(census)와 표본조사로 구분

통계자료의 획득 방법

총 조사/전수 조사(Census)

대상 집단 모두를 조사하는데 많은 비용과 시간이 소요되므로 특별한 경우를 제외하곤 사용X
ex) 인구주택 총 조사

표본조사

대부분의 설문조사가 표본조사로 진행
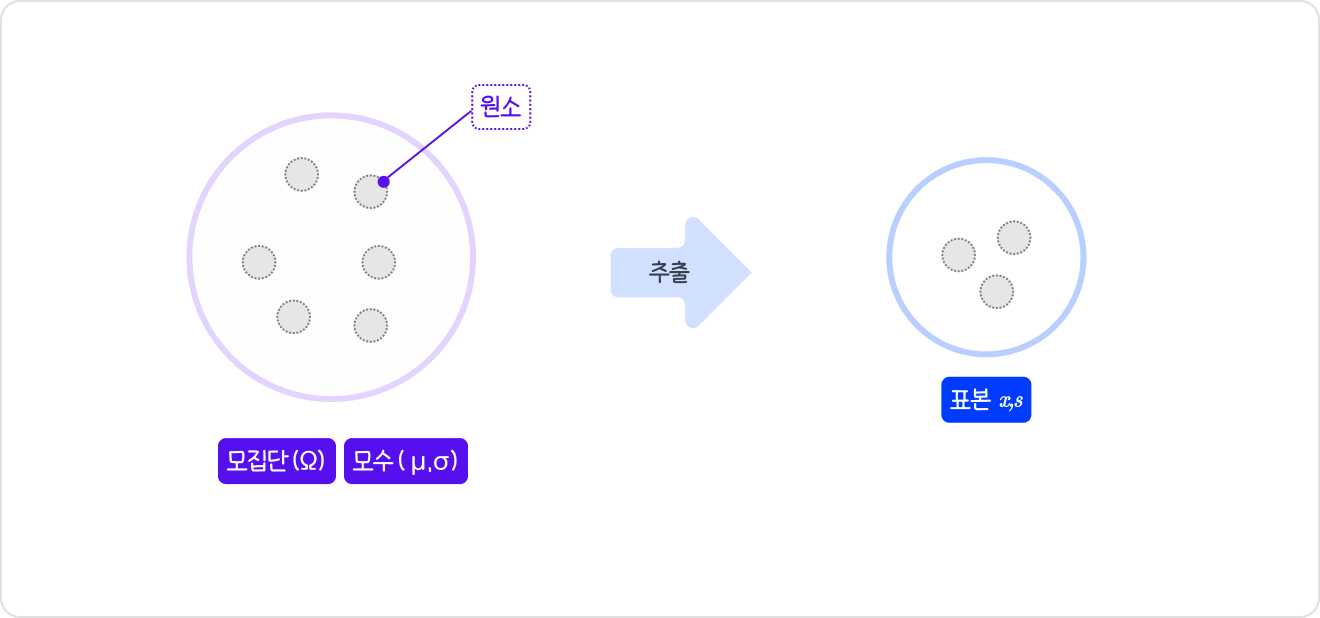
모집단에서 샘플을 추출하여 진행
모집단(Population) : 조사하고자 하는 대상 집단 전체
원소(Element) : 모집단을 구성하는 개체
표본(Sample) : 조사하기 위해 추출한 모집단의 일부 원소
모수(Parameter) : 표본 관측에 의해 구하고자 하는 모집단에 대한 정보(모집단의 특성)
모집단의 정의, 표본 크기, 조사 방법, 조사기간, 표본추출방법을 정확히 명시해야 함

*표본오차 : 모집단의 일부인 표본에서 얻은 자료를 통해 모집단 전체의 특성을 추론함으로써 생기는 오차.
-> 모집단을 대표할 수 있는 표본단위들이 조사대상으로 추출되지 못하면 발생

*비표본오차 : 표본오차를 제외한 조사의 전체 과정에서 발생할 수 있는 모든 오차

*표본편의 : 표본추출방법에서 기인하는 오차.
-> 표본추출이 의도된 모집단의 일부 구성원이 다른 구성원보다 더 낮거나 더 높은 표본 추출 확률을 갖는 오차

표본 추출 방법

표본조사의 중요한 점은 모집단을 대표할 수 있는 표본추출
표본 추출 방법에 따라 분석결과의 해석은 큰 차이 발생

(N개의 모집단에서 n개의 표본을 추출하는 경우)

단순랜덤 추출법(Simple Random Sampling)

각 샘플에 번호를 부여해 임의의 n개를 추출하는 방법
각 샘플은 선택될 확률이 동일
비복원, 복원(추출한 원소를 다시 집어넣어 추출하는 경우)추출

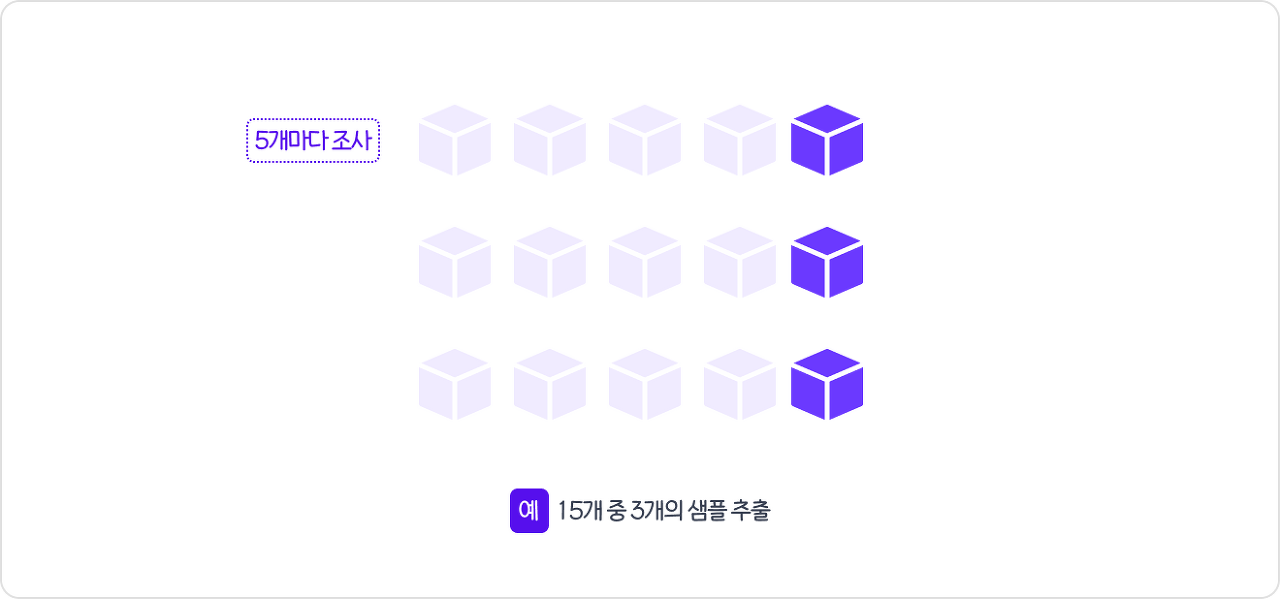
계통추출법(Systematic Sampling)

단순랜덤추출법의 변형된 방식
번호를 부여한 샘플을 나열하여 K개씩 (K=N/n) n개의 구간으로 나누고 첫 구간(1, 2, ... , K)에서 하나를 임의로 선택한 후에 K개씩 띄어서 n개의 표본 선택

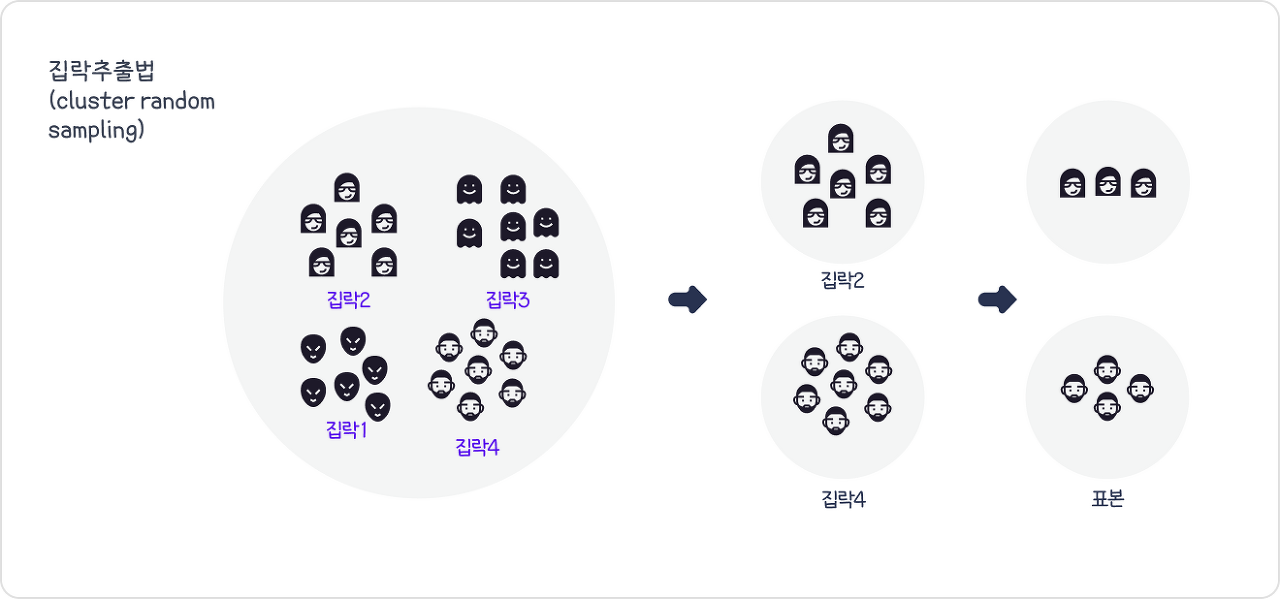
집락추출법(Cluster Random Sampling)

군집을 구분하고 군집별로 단순랜덤 추출법을 수행한 후, 모든 자료를 활용/샘플링하는 방법
지역표본추출, 다단계표본추출

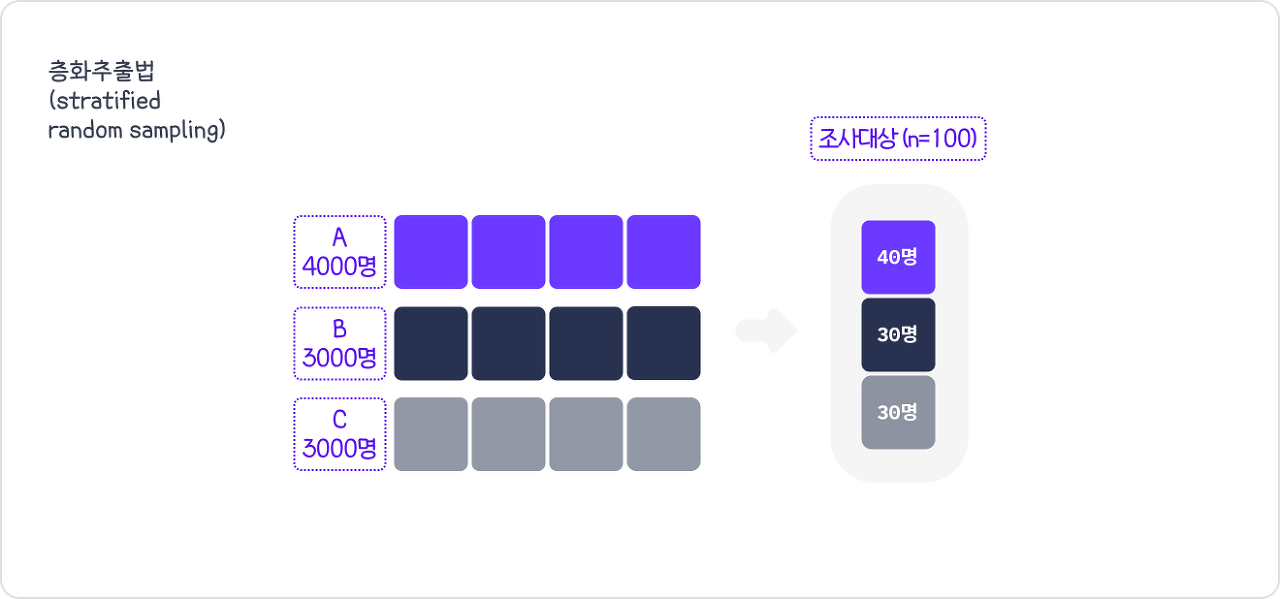
층화추출법(Stratified Random Sampling)

이질적인 원소들로 구성된 모집단에서 각 계층을 고루 대표할 수 있도록 표본을 추출하는 방법
유사한 원소끼리 몇 개의 층(Stratum)으로 나누어 각 층에서 랜덤 추출
비례층화추출법, 불비례층화추출법

*실험 : 특정 목적 하에서 실험 대상에게 처리를 가한 후, 그 결과를 관측해 자료를 수집하는 방법

측정(Measurement)

표본조사나 실험을 실시하는 과정에서 추출된 원소들이나 실험 단위로부터 주어진 목적에 적합하도록 관측해 자료를 얻는 것

측정방법

서열척도는 명목척도와 달리 매겨진 숫자의 크기를 의미있게 활용 가능
ex) 1등이 2등보다 성적이 높다
구간척도는 절대적 크기를 측정할 수 없기 때문에 사칙연산중 더하기/빼기는 가능하나 비율처럼 곱하기/나누기는 불가능

통계분석

특정한 집단이나 불확실한 현상을 대상으로 자료를 수집해 대상 집단에 대한 정보를 구하고, 적절한 통계분석 방법을 이용해 의사결정을 하는 과정

기술통계(Descriptive Statistic)
: 주어진 자료로부터 어떠한 판단이나 예측과 같은 주관이 섞일 수 있는 과정을 배제하여 통계집단들의 여러 특성을 수량화하여 객관적인 데이터로 나타내는 통계분석 방법론

Sample에 대한 특성인 평균, 표준편차, 중위수, 최빈값, 그래프 ,왜도, 첨도 등을 구하는 것

통계적 추론(추측통계, Inference Statistics)
: 수집된 자료를 이용해 대상 집단(모집단)에 대한 의사결정을 하는 것

Sample을 통해 모집단을 추정하는 것

모수추정
: 표본집단으로부터 모집단의 특성인 모수(평균/분산 등)를 분석하여 모집단 추론
가설검정
: 대상집단에 대해 특정한 가설을 설정한 후, 그 가설이 옳은지 그른지에 대한 채택여부를 결정하는 방법론
예측
: 미래의 불확실성을 해결해 효율적인 의사결정을 하기 위해 활용
ex) 회귀분석, 시계열분석 등

확률 및 확률분포

확률

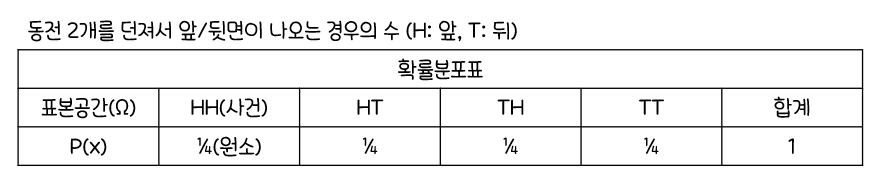
표본공간 S에 부분집합인 각 사상에 대해 실수값을 가지는 함수의 확률값이 0과 1 사이에 있고, 전체 확률의 합이 1인 것
표본공간 Ω의 부분집합인 사건 E의 확률은 표본공간 원소의 개수에 대한 사건 E의 개수 비율로 확률을 P(E)라고 할 때, 아래로 정의

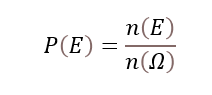
표본공간(Sample Space, Ω)
: 어떤 실험을 실시할 때 나타날 수 있는 모든 결과들의 집합
사건(Event)
: 관찰자가 관심이 있는 사건으로 표본공간의 부분집합
원소(Element)
: 나타날 수 있는 개별의 결과
확률변수(Random Variable)
: 특정값이 나타날 가능성이 확률적으로 주어지는 변수

정의역(Domain)이 표본공간, 치역(Range)이 실수값(0<y<1)인 함수
0이 아닌 확률을 갖는 실수값의 형태에 따라 이산형 확률변수와 연속형 확률변수로 구분
확률변수X의 기대값(Expectation, Expected Value) : 실험을 반복했을 때 평균적으로 기대할 수 있는 값
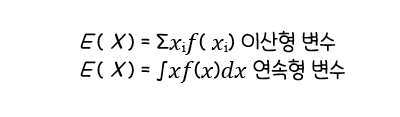
확률변수 X의 k차 적률(k-th Moment)
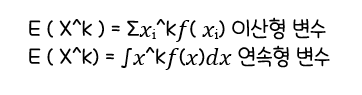
확률변수 X의 k차 중심적률(k-th Cental Moment)
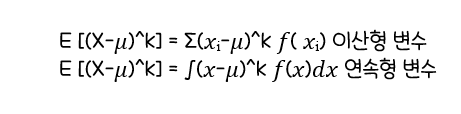
2차 중심적률 E [(X-𝜇)^2]=𝜎^2 : 모분산(Population Variance) 기대값의 선형성 이용

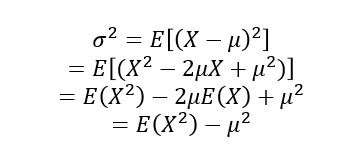
-> 즉, 모분산=2차적률-1차적률^2로 해석

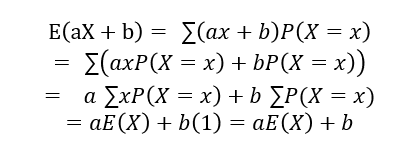
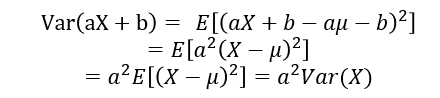
덧셈정리(배반사건X) : 사건A와 사건B가 동시에 일어날 수 있을 때(교집합이 성립할 때),
일어날 확률P(A 또는 B) : P(AUB)=P(A)+P(B)-P(A∩B)
=> 사건B가 주어졌을 때 사건A의 조건부 확률
: P(A|B)=P(A∩B)/P(B)
덧셈정리(배반사건O) : 사건A와 사건B가 동시에 일어나지 않을 때,
즉 사건A 또는 사건 B 중 어느 한 쪽만 일어날 확률 : P(AUB)=P(A)+P(B)
곱셈정리 : 사건A와 B가 서로 무관계하게 나타날 때, 즉 독립사건일 때
사건A와 B가 동시에 나타날 확률 P(A와B) : P(A∩B)=P(A)XP(B)
=> 사건B가 주어졌을 때 사건A의 조건부 확률
: P(A|B)=P(A)

확률분포

이산형 확률변수
-0이 아닌 확률값을 갖는 확률 변수를 셀 수 있는 경우 (확률질량함수)
ex) 동전 2개를 던져서 앞/뒷면이 나오는 경우의 수

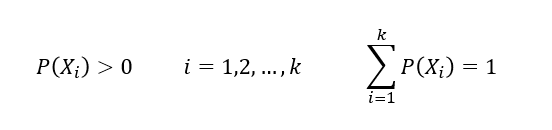
베르누이 확률분포(Bernoulli Distribution)
: 결과가 2개만 나오는 경우
ex) 동전 던지기, 시험의 합격/불합격 등
메이저리거 추신수 선수가 안타를 칠 확률은 베르누이 분포를 따름
(안타를 치는 사건을 x=1, 안타를 칠 확률은 타율로 적용 가능
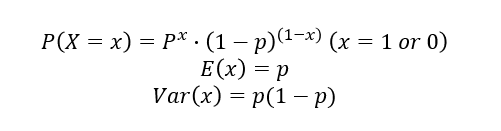
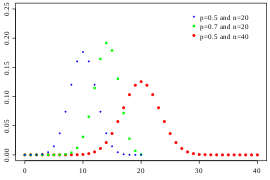
이항분포(Binomial Distribution)
: 베르누이 시행을 n번 반복했을 때 k번 성공할 확률
ex) 메이저리거 추신수 선수가 오늘 경기에서 5번 타석에 들어와서 3번 안타를 칠 확률은 이항분포를 따른다.
(n=5, k=3, 안타를 칠 확률 P(x)=타율로 적용 가능)
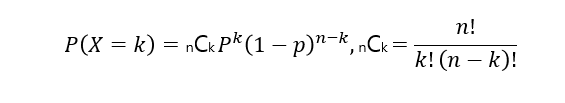
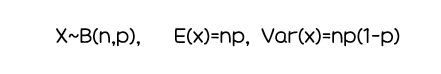
- 성공할 확률 p가 0이나 1에 가깝지 않고 n이 충분히 크면 이항분포는 정규분포에 가까워짐
- 성공할 확률 P가 1/2에 가까우면 종모양

기하분포(Geometric Distribution)
: 성공확률이 p인 베르누이 시행에서 첫 번째 성공이 있기 까지 x번 실패할 확률
ex) 메이저리거 추신수 선수가 오늘 경기에서 5번 타석에 들어와서 3번째 타석에서 안타칠 확률은 기하분포를 따름
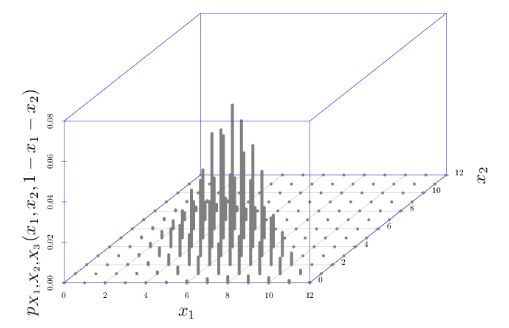
다항분포(Multinomial Distribution)
: 이항분포를 확장한 것으로,
세 가지 이상의 결과를 가지는 반복 시행에서 발생하는 확률 분포

포아송분포(Poisson Distribution)
: 시간과 공간 내에서 발생하는 사건의 발생 횟수에 대한 확률분포
ex) 책에 오타가 5page당 10개씩 나온다고 할 때, 한 페이지에 오타가 3개 나올 확률
메이저리거 추신수 선수가 최근 5경기에서 10개의 홈런을 쳤을 때, 오늘 경기에서 홈런을 못 칠 확률은 포아송분포를 따름

연속형 확률변수
-가능한 값이 실수의 어느 특정구간 전체에 해당하는 확률변수(확률밀도함수)

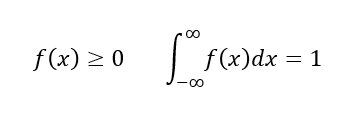
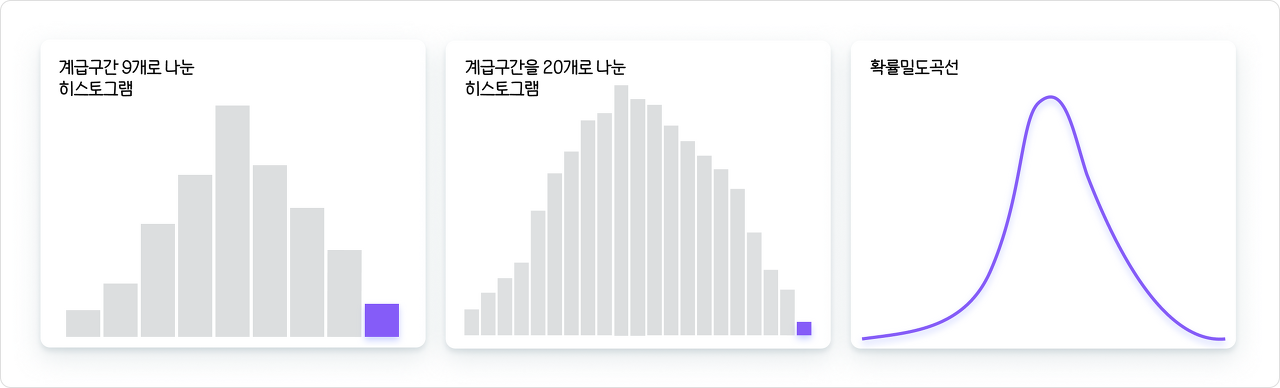
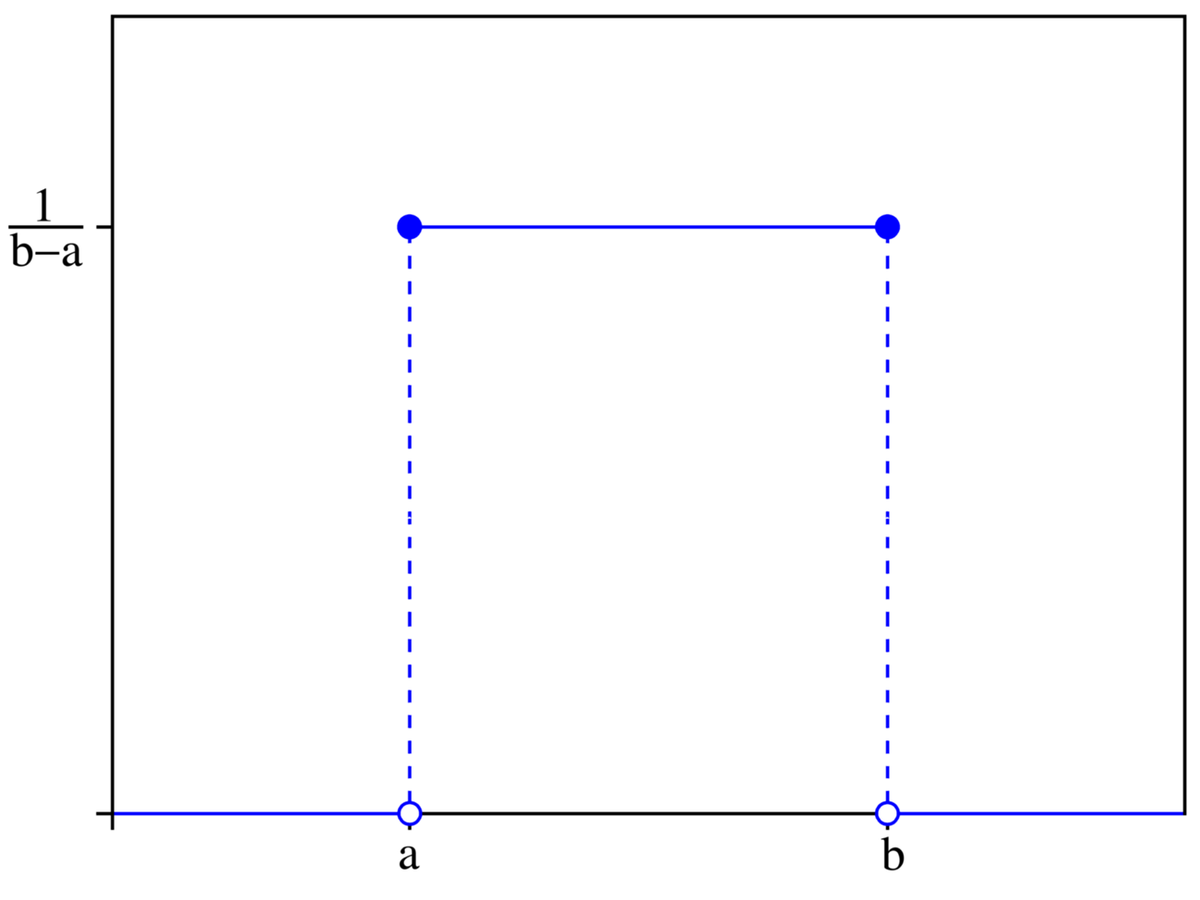
균일분포(일양분포, Uniform Distribution)
: 모든 확률변수 X가 균일한 확률을 가지는 확률분포
ex) 다트의 확률분포

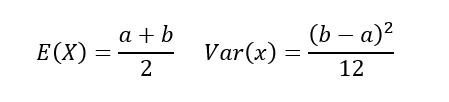
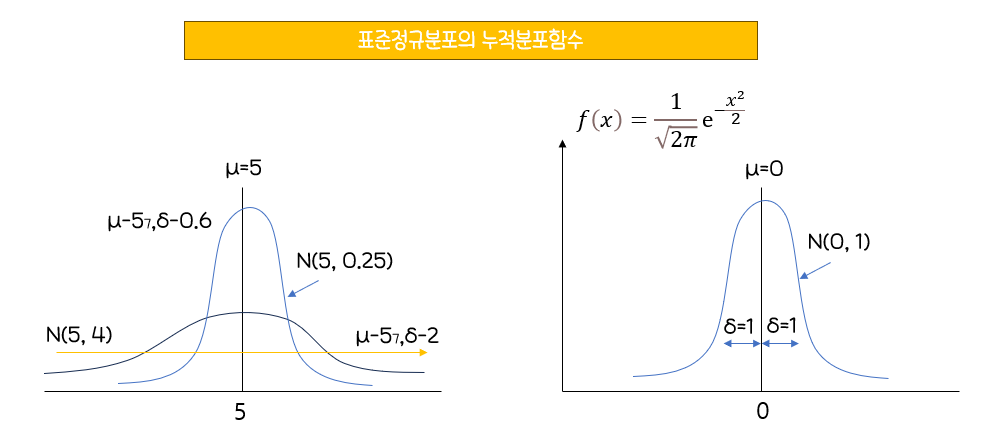
정규분포(Normal Distribution)
: 평균이 𝜇이고, 표준편차가 𝜎인 x의 확률밀도함수
- 표준편차가 클 경우 퍼져보이는 그래프가 나타남

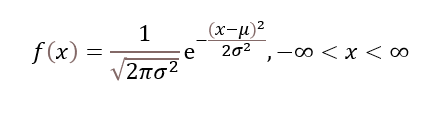
*최소-최대 정규화(Min-Max Normalization)
: (X-Min)/(Max-Min), 원 데이터의 분포를 유지하면서 0~1 사이 값이 되도록 정규화함

*Z-점수 표준화(Z-Score Standardization)
: (X-평균)/표준편차, 원 데이터를 표준정규분포에 해당되도록 표준화

*표준정규분포
: 평균이 0이고 표준편차가 1인 정규분포
-정규분포를 표준정규분포로 만들기 위해선 Z=(X-µ)/𝜎(Z-점수 표준화)식 이용

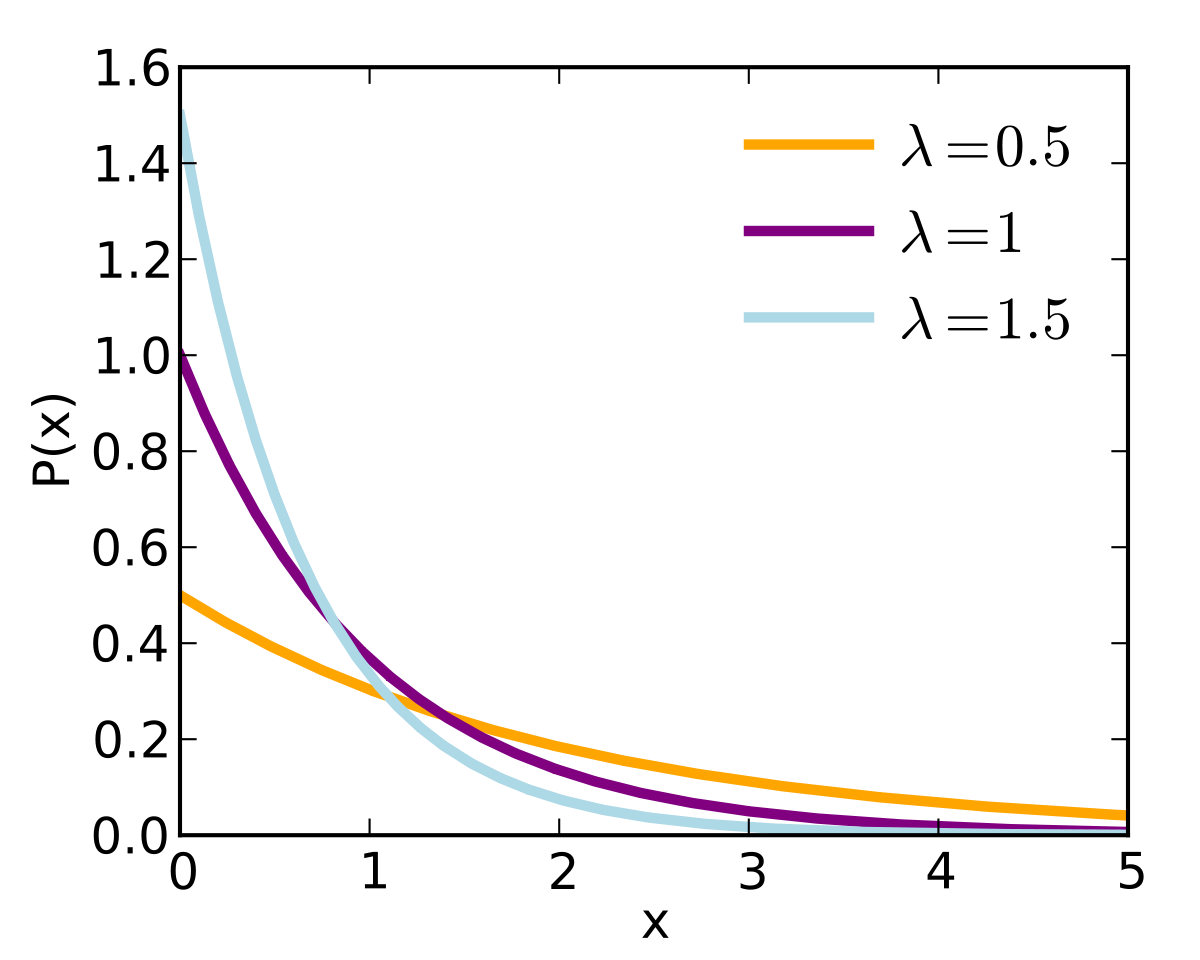
지수분포(Exponential Distribution)
: 어떤 사건이 발생할 때까지 경과 시간에 대한 연속확률분포
ex) 전자레인지의 수명시간, 콜센터에 전화가 걸려올 때까지의 시간, 은행에 고객이 내방하는데 걸리는 시간, 정류소에서 버스가 올 때까지의 시간

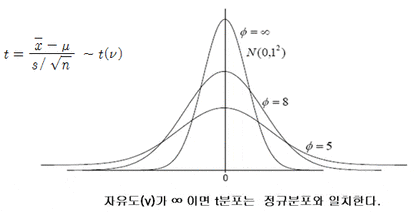
t-분포(t-Distribution)
: 표준정규분포와 같이 평균이 0을 중심으로 좌우가 동일한 분포
- 표본의 크기가 적을 때 : 표준정규분포를 위에서 눌러놓은 것
- 표본이 커져서(30개 이상) : 자유도가 증가하면 표준정규분포와 거의 같은 분포
- 데이터가 연속형일 경우 활용
- 두 집단의 평균이 동일한지 알고자 할 때 검정통계량으로 활용

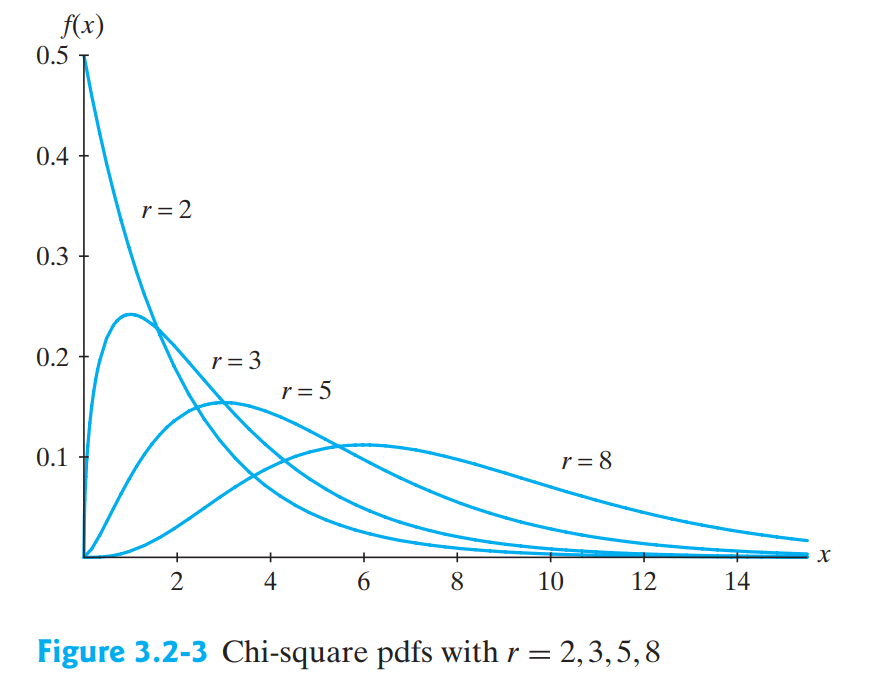
χ2-분포(카이제곱분포/Chi-Square Distribution)
: 모평균과 모분산이 알려지지 않은 모집단의 모분산에 대한 가설검정에 사용되는 분포
- 두 집단 간의 동질성 검정에 활용
- 범주형 자료에 대해 얻어진 관측값과 기대값의 차이를 보는 적합성 검정
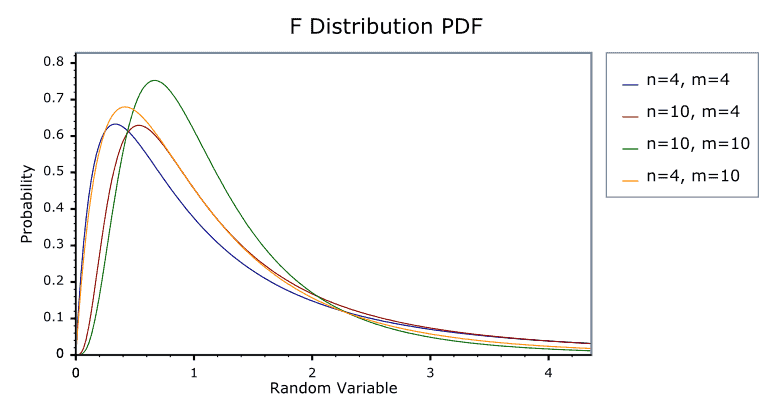
F-분포(F-Distribution)
: 두 집단 간 분산의 동일성 검정에 사용되는 검정 통계량 분포
- 확률변수는 항상 양의 값만을 갖고 χ2분포와 달리 자유도를 2개가지고 있으며 자유도가 커질수록 정규분포에 가까워짐

추정과 가설검정

추정의 개요

확률표본(Random Sample)

확률분포는 분포를 결정하는 평균, 분산 등의 모수(Parameter)를 가짐
특정한 확률분포로부터 독립적으로 반복해 표본을 추출
각 관찰값들은 서로 독립적이며 동일한 분포를 갖음

추정

표본으로부터 미지의 모수를 추측하는 것
점추정과 구간추정으로 구분
- 점추정(Point Estimation)
  : 모수가 특정한 값일 것이라고 추정
  - 표본의 평균, 중위수, 최빈값 등을 사용
- 구간추정(Interval Estimation)
  : 점추정의 정확성 보완을 위해 확률로 표현된 믿음의 정도 하에서 모수가 특정한 구간에 있을 것이라고 선언하는 것
  - 항상 추정량의 분포에 대한 전제가 주어져야 하고, 구해진 구간 안에 모수가 있을 가능성의 크기(신뢰수준)이 주어져야 함
  - n : 전체 표본수

가설검정

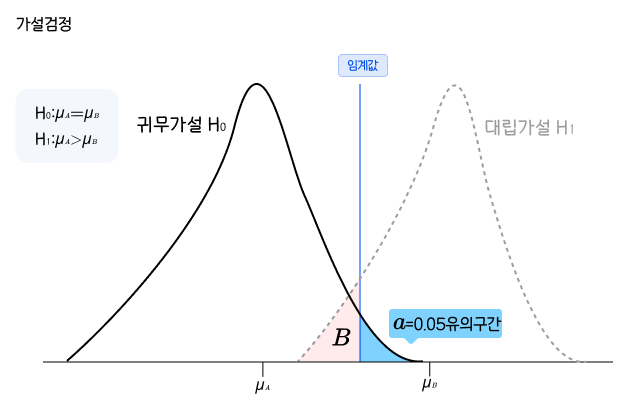
모집단에 대한 어떤 가설을 설정한 뒤에 표본관찰을 통해 그 가설의 채택여부를 결정하는 분석방법
표본관찰 또는 실험을 통해 귀무가술과 대립가설 중 하나를 선택하는 과정
귀무가설이 옳다는 전제하에 검정통계량 값을 구한 후에 이 값이 나타날 가능성의 크기에 의해 귀무가설 채택여부 결정

귀무가설(Null Hypothesis, 𝐻0)
: 비교하는 값과 차이가 없다, 동일하다를 기본개념으로 하는 가설
대립가설(Alternative Hypothesis, 𝐻1)
: 뚜렷한 증거가 있을 때 주장하는 가설
검정통계량(Test Statistic)
: 관찰된 표본으로부터 구하는 통계량.
검정 시 가설의 진위 판단 기준
유의수준(Significance Level, 𝛼)
: 귀무가설을 기각하게 되는 확률의 크기.
-> 귀무가설이 옳은데도 이를 기각하는 확률의 크기
기각역(Critical Region, C)=P-value=유의구간
: 귀무가설이 옳다는 전제 하에서 구한 검정통계량의 분포에서 확률이 유의수준 𝛼인 부분
->반대 : 채택역(Acceptance Region)

*유의확률(p-value)
: 귀무가설이 맞다고 가정할 때 얻을 수 있는 결과보다 실제값이 더 극단에 위치할 확률

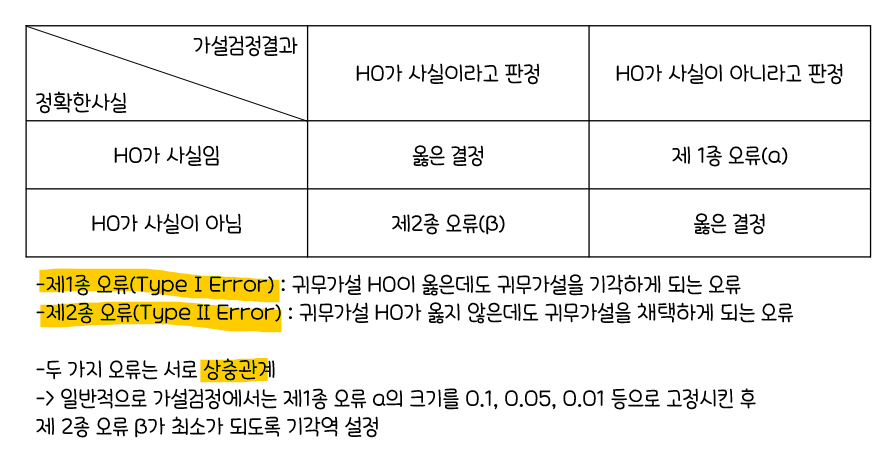
*검정력(Statistical Power)
: 대립가설이 사실일 때, 대립가설을 채택하는 옳은 결정을 할 확률

비모수 검정

모수적 방법
: 검정하고자 하는 모집단의 분포에 대한 가정을 하고, 그 가정하에서 검정통계량과 검정통계량의 분포를 유도해 검정을 실시

비모수적 방법
: 자료가 추출된 모집단의 분포에 대한 아무 제약을 가하지 않고 검정을 실시

관측된 자료가 특정분포를 따른다고 가정할 수 없는 경우에 이용
관측된 자료의 수가 많지 않거나(30개 미만) 자료가 개체 간의 서열관계를 나타내는 경우에 이용

모수적 검정과 비모수 검정의 차이점

가설의 설정

모수적 검정
: 가정된 분포의 모수에 대해 가설 설정
비모수 검정
: 가정된 분포가 없으므로 가설은 단지 '분포의 형태가 동일하다' 또는 '분포의 형태가 동일하지 않다' 와 같이 분포의 형태에 대해 설정

검정 방법

모수적 검정
: 관측된 자료를 이용해 구한 표본평균, 표본분산 등을 이용해 검정 실시
비모수 검정
: 관측값의 절대적인 크기에 의존하지 않는 관측값들의 순위(Rank)나 두 관측값 차이의 부호등을 이용해 검정

비모수 검정 예

부호검정(Sign Test)
윌콕슨의 순위합 검정(Wilcoxon's Rank Sum Test)
윌콕슨의 부호 순위 검정(Wilcoxon's Signed Rank Test)
맨-휘트니의 U검정(Mann-Whitney U test)
런 검정(Run Test)
스피어만의 순위상관계수(Spearmans's rank correlation analysis)

🧈기초 통계분석

기술통계(Descriptive Statistics)

자료의 특성을 표, 그림, 통계량 등을 사용하에 쉽게 파악할 수 있도록 정리/요약하는 것
자료를 요약하는 기초적 통계
데이터 분석에 앞서 데이터의 대략적인 통계적 수치를 계산함으로써 데이터에 대한 대략적인 이해와 앞으로 분석에 대한 통찰력을 얻기에 유리
객관적인 데이터

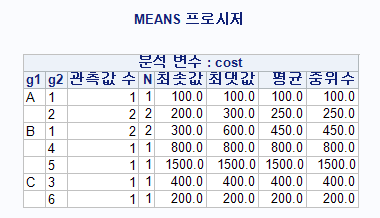
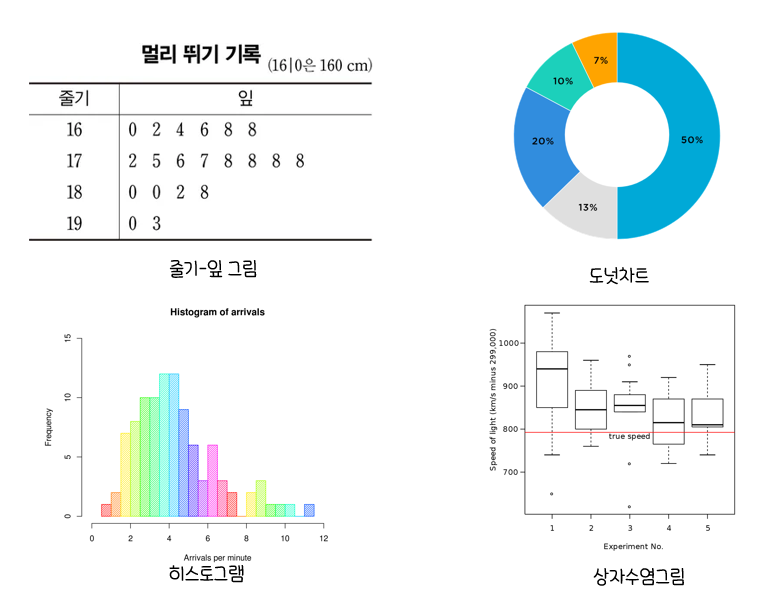
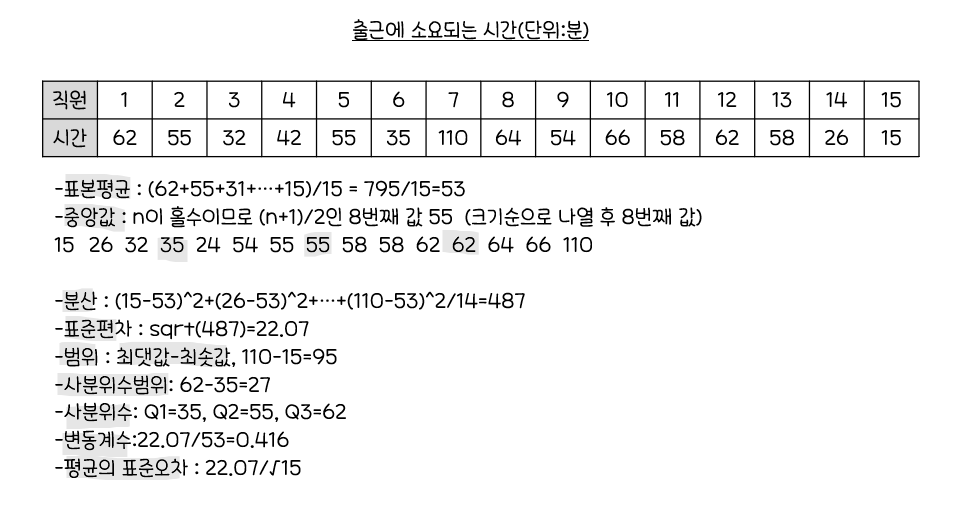
통계량에 의한 자료 정리

중심위치의 측도

자료(데이터)

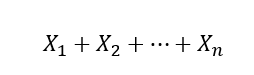
표본평균(Sample Mean)
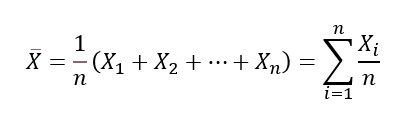
중앙값(Median)
: 자료를 크기순으로 나열할 때 중앙에 위치하는 자료값

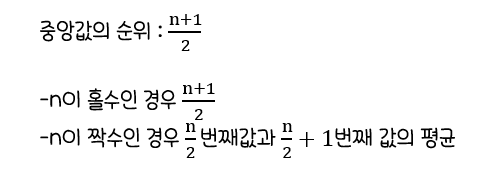
산포의 측도
-대표적인 산포도(Dispersion) : 분산, 표준편차, 범위 및 사분위수범위

분산
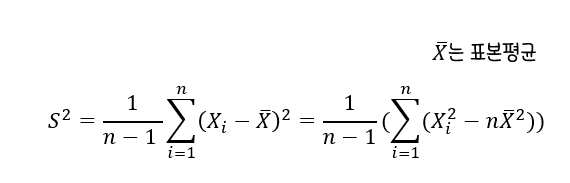
표준편차
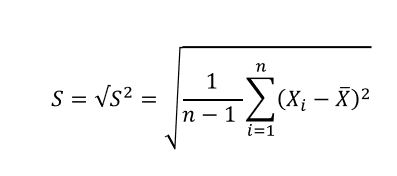
사분위수범위(Interquartile Range)
- IQR : Q3-Q1
사분위수
- 제 1사분위수(Q1)=25%
- 제 2사분위수(Q2)=50%
- 제 3사분위수(Q3)=75%

백분위수(Percentile)

변동계수(Coefficient of Variation)
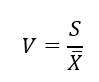
표본평균의 표준오차

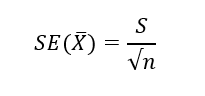
분포의 형태에 관한 측도

왜도
: 분포의 비대칭정도를 나타내는 측도

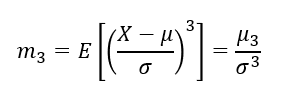
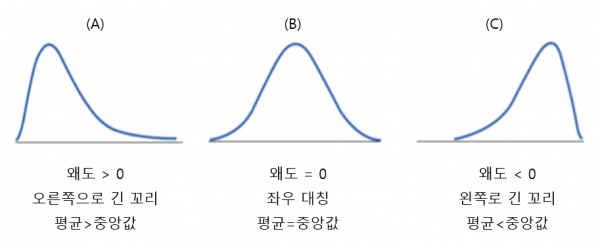
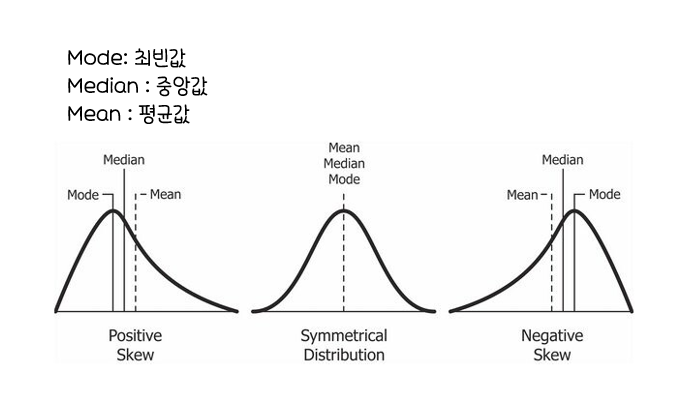
첨도
: 분포의 중심에서 뾰족한 정도를 나타내는 측도

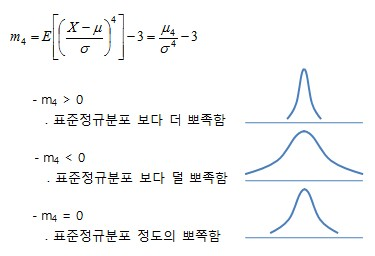
그래프를 이용한 자료 정리

히스토그램
: 표로 되어 있는 도수 분포를 그림으로 나타낸 것.
-도수분포표를 그래프로 나타낸 것
모자이크 플롯(Mosaic Plot)
: 교차표(2원, 3원)를 시각화한 그래프.
-사각형들이 그래프에 나열되고 사각형의 넓이는 범주에 속한 데이터 수(또는 비율)
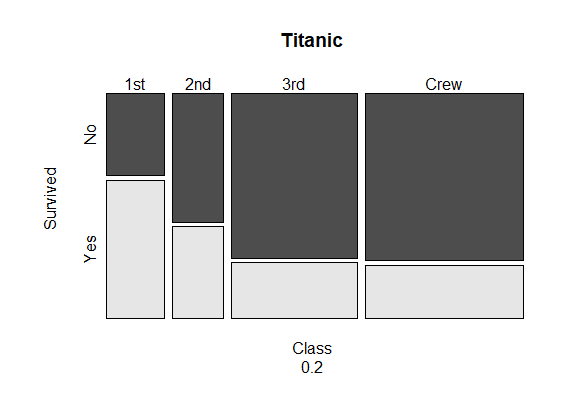
막대그래프와 히스토그램의 비교

막대그래프
: 범주(Category)형으로 구분된 데이터(ex. 직업, 종교, 음식 등)를 표현하며 범주의 순서를 의도에 따라 바꾸기 o
히스토그램
: 연속(Continuous)형으로 표시된 데이터(ex. 몸무게, 성적, 연봉 등)를 표현하며 임의로 순서 바꾸기x, 막대간 간격x

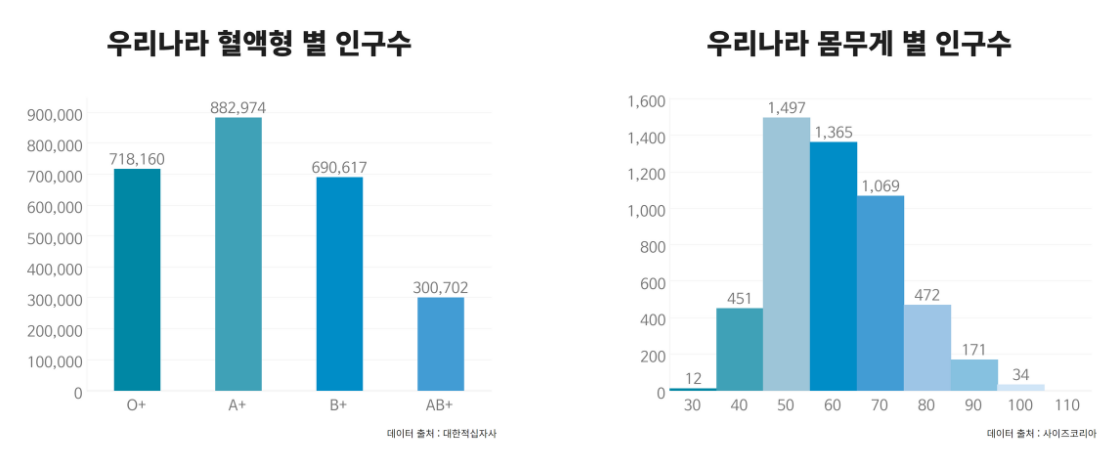
히스토그램의 생성
: 데이터의 수를 활용해서 계급의 수와 계급간격을 계산하여 도수분포표를 만들고 히스토그램 생성
-계급의 수 : 2^k>=n을 만족하는 최소의 정수 log2n=k에서 최소의 정수
(k는 계급 수, n은 데이터 수)

계급의 간격은 (최댓값-최솟값)/계급수
계급의 수와 간격이 변하면 히스토그램 모양이 변함

줄기-잎 그림(Stem-and Leaf Plot)
: 데이터를 줄기와 잎의 모양으로 그린 그림
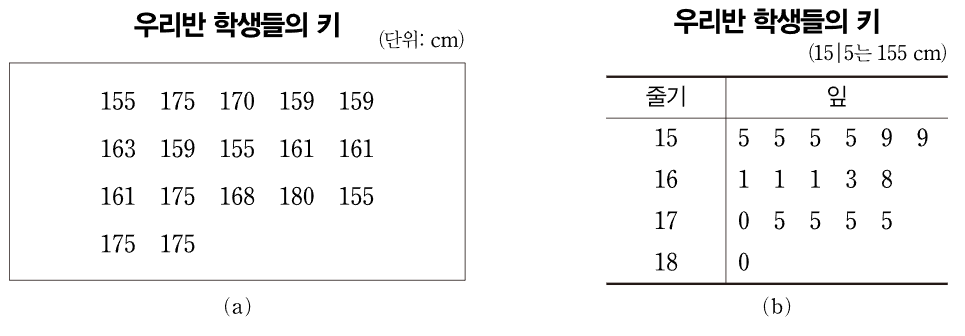
상자그림(Box Plot)
: 다섯 숫자 요약(최솟값, Q1, Q2, Q3, 최댓값)을 통해 그림으로 표현
-사분위수범위(IQR) : Q3-Q1
-안울타리(Inner Fence) : Q1-1.5xIQR ~ Q3+1.5xIQR
-바깥울타리(Outer Fence) : Q1-3xIQR ~ Q3+3xIQR
-보통이상점(Mild Outlier) : 안쪽울타리와 바깥 울타리 사이 자료
-극단이상점(Extreme Outlier) : 바깥울타리 밖의 자료

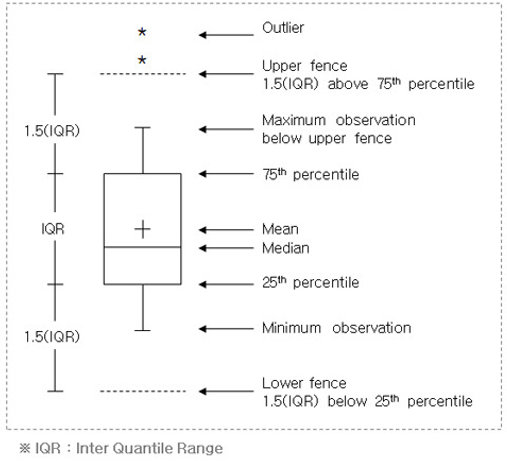
*R에서의 분위수

#특정 컬럼의 분위수를 알고 싶을 때 사용
quantile(data명$column명)

인과관계의 이해

종속변수(반응변수, y) : 다른 변수의 영향을 받는 변수

독립변수(설명변수, x) : 영향을 주는 변수

산점도(Scatter Plot) : 좌표평면 위에 점들로 표현한 그래프

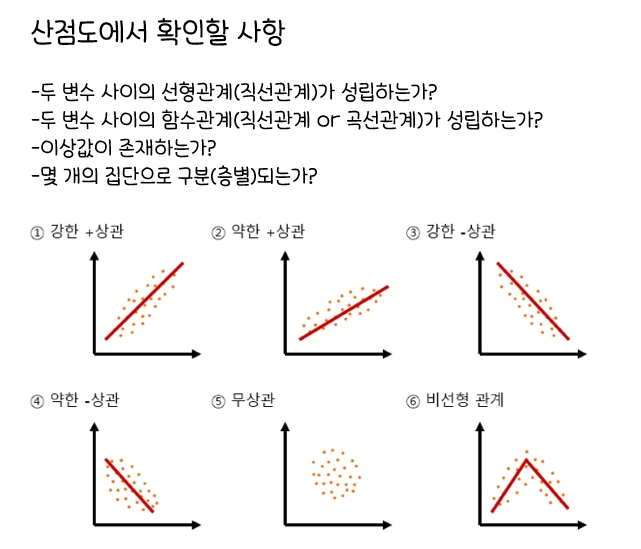
공분산(Covariance)
: 두 확률변수 X, Y의 방향의 조합(선형성)

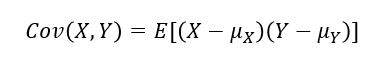
공분산의 부호만으로 두 변수 간의 방향성을 확인 가능
부호가 + : 두 변수는 양의 방향성
부호가 - : 두 변수는 음의 방향성
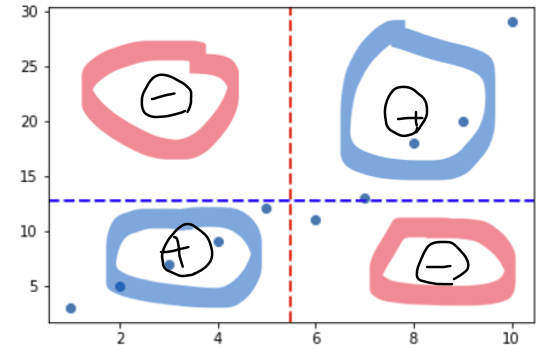
X, Y가 서로 독립 : Cov(X,Y)=0

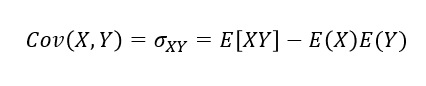
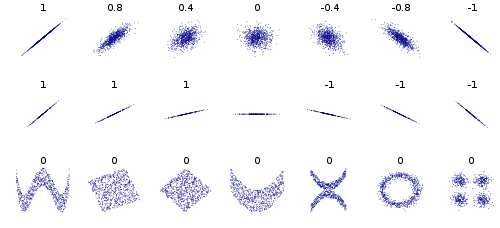
상관분석(Correlation Analysis)

두 변수간의 관계의 정도를 알아보기 위한 분석방법
두 변수의 상관관계를 알아보기 위해 상관계수(Correlation Coefficient)를 이용

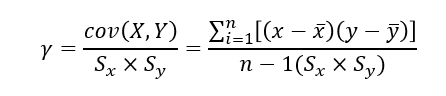
상관관계 특성

상관계수 범위	해석
0.7<𝛾<=1	강한 양(+)의 상관
0.3<𝛾<=0.7	약한 양(+)의 상관
0<𝛾<=0.3	거의 상관 없음
𝛾=0	상관관계(선형, 직선)가 존재X
-0.3<=𝛾<0	거의 상관 없음
-0.7<=𝛾<-0.3	약한 음(-)의 상관
-1<=𝛾<-0.7	강한 음(-)의 상관

상관분석의 유형

상관분석을 위한 R코드
-x: 숫자형 변수, y:NULL(default) 또는 변수, na.rm : 결측값 처리

분산(var)

var(x,y=NULL, na.rm=FALSE)

공분산(cov)

cov(x,y=NULL, use="everything", method=c("pearson","kendall","spearman"))

상관관계(cor/rcorr)

cor(x, y=NULL, use="everything", method=c("pearson","kendall","spearman"))

#Hmisc패키지의 rcorr사용
rcorr(matrix(data명), type=c("pearson","kendall","spearman"))
rcorr(x, y, type = c("pearson", "spearman"))

상관분석의 가설 검정

상관계수 𝛾가 0이면 입력변수 x와 출력변수 y사이에는 아무런 관계가 없다.
(귀무가설 : 𝛾=0, 대립가설 : 𝛾!=0)
t-검정통계량을 통해 얻은 p-value 값이 0.05이하인 경우 대립가설을 채택하게 되어 우리가 데이터를 통해 구한 상관계수를 활용가능

상관분석 예제

datasets 패키지의 mtcars라는 데이터셋의 마일(mpg), 총마력(hp)의 상관관계 분석 실시

data(mtcars)
a<-mtcars$mpg
b<-mtcars$hp
cov(a,b)
cor(a,b)
cor.test(a,b,method="pearson")

결과 및 해석

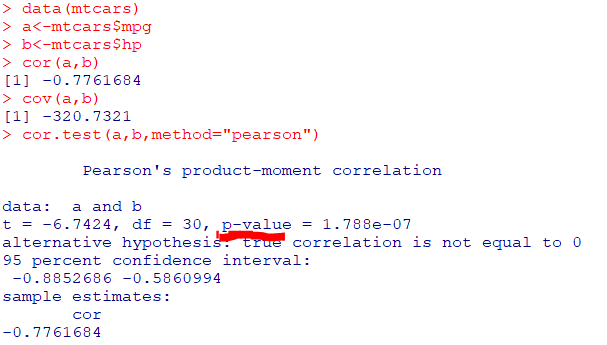
mtcars 데이터셋의 mpg와 hp를 각각 a,b에 저장하여 mpg와 hp의 공분산(cov), 상관계수(cor)를 구함
공분산은 -320.7321, 상관계수는 -0.7761684
-> mpg와 hp는 공분산으로 음의 방향성을 가짐을 알 수 있고,
상관계수로 강한 음의 상관관계가 있음을 알 수 있음
cor.test를 이용해 상관관계 분석을 실행
p-value가 1.788e-07로 유의수준 0.05보다 작게나타나 상관관계가 있음
-> p-value가 0.05보다 작으면 통계적으로 유의미

🍠회귀분석

회귀분석의 개요

하나나 그 이상의 독립변수들이 종속변수에 미치는 영향을 추정할 수 있는 통계기법
변수들 사이의 인과관계를 밝히고 모형을 적합하여 관심있는 변수를 예측하거나 추론하기 위한 분석방법
독립변수의 개수가 하나이면 단순선형회귀분석,
독립변수의 개수가 두 개 이상이면 다중선형회귀분석

회귀분석의 변수

영향을 받는 변수(y) : 반응변수(Response Variable), 종속변수(Dependent Variable), 결과변수(Outcome Variable)
영향을 주는 변수(x) : 설명변수(Explanatory Variable) , 독립변수(Independent Variable), 예측변수(Predictor Variable)

선형회귀분석의 가정

선형성
: 입력변수와 출력변수의 관계가 선형
(선형회귀분석에서 가장 중요한 가정)
등분산성(분산이 같음)
: 오차의 분산이 입력변수와 무관하게 일정.
-잔차플롯(산점도)을 활용하여 잔차(표본으로 추정한 회귀식과 실제 관측값의 차이)와 입력변수간에 아무런 관련성이 없게 무작위적으로 고루 분포되어야 등분산성 가정 만족
독립성
: 입력변수와 오차는 관련X
-자기상관(독립성)을 알아보기 위해 Durbin-Waston 통계량 사용
-시계열 데이터에서 많이 활용
비상관성
: 오차들끼리 상관X
정상성(정규성)
: 오차의 분포가 정규분포를 따름.
-Q-Q plot, Kolmogorov-Smirnov 검정, Shaprio-Wilk 검정등을 활용해 정규성 확인

*Anderson-Darling Test
: 콜모고로프-스미르노프 검정(K-S검정)을 수정한 적합도 검정
-특정분포의 꼬리(Tail)에 K-S검정보다 가중치를 더 두어 수행
-여러 분포의 적합도 검정이 가능하지만 정규성 검정에 강력

*D'Agostino-Pearson Test
: 왜도와 첨도를 사용해 데이터가 정규분포를 따르는지 검정(표본크기 20이상)

*Jarque-Bera Test
: 정규분포의 기대 왜도와 첨도가 데이터에서 얻은 값과 일치하는지 검정

그래프를 활용한 선형회귀분석의 가정 검토

선형성
: 선형회귀모형에서는 아래 Linear 그래프와 같이 설명변수(x)와 반응변수(y)가 선형적 관계에 있음이 전제되어야 함
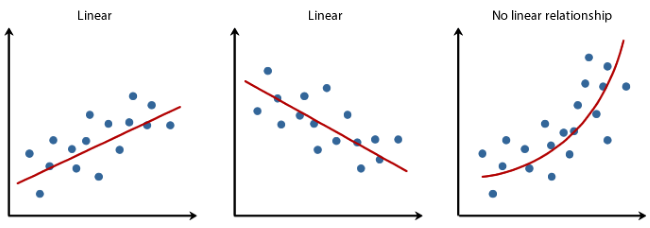
등분산성
: 설명변수(x)에 대한 잔차의 산점도를 그렸을 때, 아래 첫번째 그래프처럼 설명변수(x)값에 관계없이 잔차들의 변동성(분산)이 일정한 형태를 보이면 선형회귀분석의 가정 중 등분산성 만족
-등분산 가정이 무너진 그래프는 설명변수(x)가 커질수록 잔차의 분산이 줄어드는 이분산의 형태
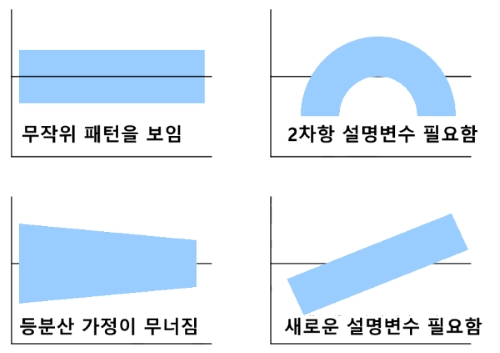
정규성
: Q-Q Plot 출력시 아래처럼 잔차가 대각방향의 직선 형태를 지니고 있으면 잔차는 정규분포를 따른다고 할 수 있음.

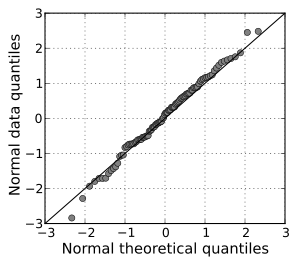
가정에 대한 검증

단순선형회귀분석
: 입력변수와 출력변수간의 선형성을 점검하기 위해 산점도 확인
다중선형회귀분석
: 선형성, 등분산성, 독립성, 정상성이 모두 만족하는지 확인

단순선형회귀분석

하나의 독립변수가 종속변수에 미치는 영향을 추정하는 통계기법

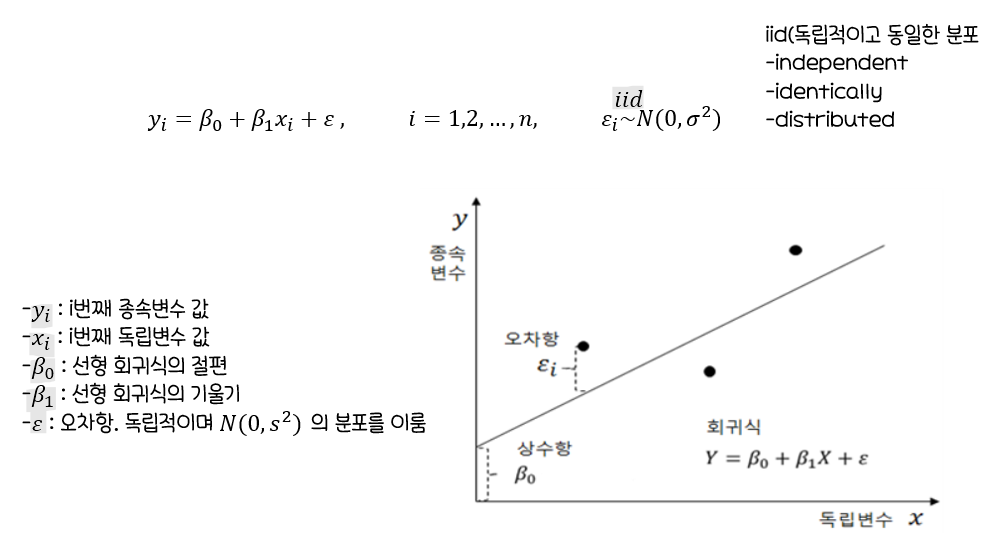
회귀분석에서의 검토사항

회귀계수들이 유의미한가?
: 해당 계수의 t-통계량(평균)의 p-값이 0.05보다 작으면 회귀계수가 통계적으로 유의
모형이 얼마나 설명력을 갖는가?
: 결정계수(𝑅^2) 확인
-결정계수는 0~1값을 가지며, 높은 값을 가질 수록 추정된 회귀식의 설명력이 높음
모형이 데이터를 잘 적합하고 있는가?
: 잔차를 그래프로 그리고 회귀진단

회귀계수의 추정(최소제곱법, 최소자승법)
: 측정값을 기초로 하여 적당한 제곱합을 만들고 그것을 최소로 하는 값을 구하여 측정결과를 처리하는 방법

잔차제곱이 가장 작은 선을 구하는 것

회귀분석의 검정

회귀계수의 검정

회귀계수 β1이 0 : 입력변수 x와 출력변수 y 사이에는 아무런 인과관계X
->회귀계수 β1이 0이면 적합된 추정식은 아무 의미 없음

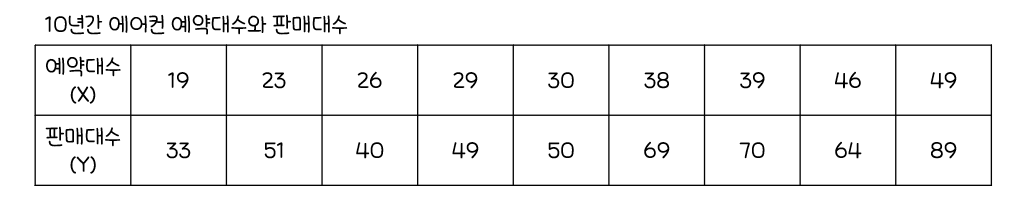
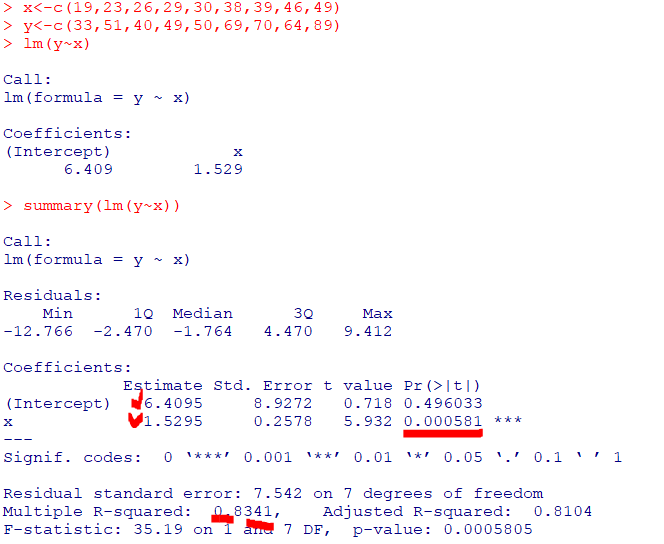
x의 회귀계수인 t-통계량에 대한 p-값 : 0.000581
-> 유의수준인 0.05보다 작으므로 회귀계수 추정치들이 통계적으로 유의
Intercept(절편) : 6.409, x(기울기) : 1.529
결정계수(R-squared) : 0.8341
-> 이 회귀식이 데이터를 적절하게 설명하고 있다곤 할 수 있음
결정계수가 높아 데이터의 설명력이 높고 회귀분석결과에서 회귀식과 회귀계수들이 통계적으로 유의미하므로 에어컨 판대매수를 에어컨 예약대수로 추정 가능
-> 회귀식 : "판매대수(y)=6.4095+1.2595*예약대수(x)"

결정계수

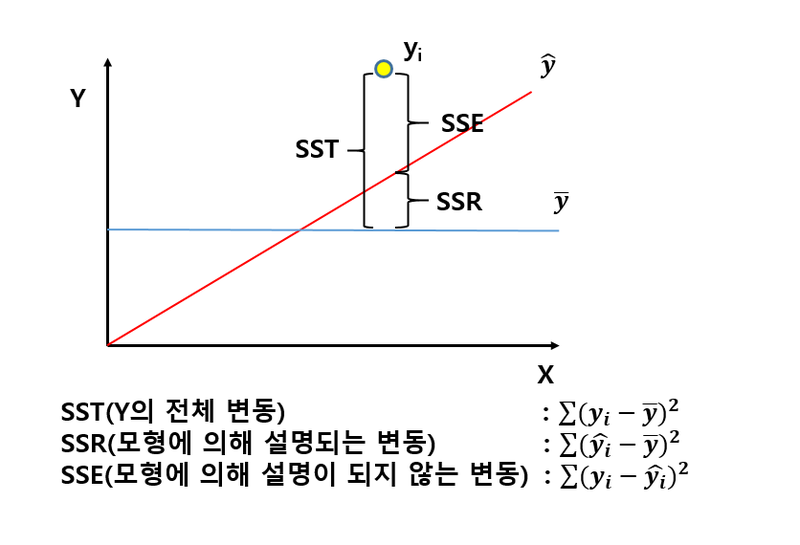
전체제곱합(Total Sum of Squares, SST)
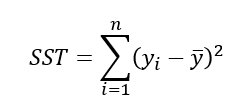
회귀제곱합(Regression Sum of Squares, SSR)
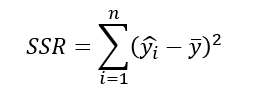
오차제곱합(Error Sum of Squares, SSE)
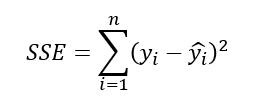
결정계수(R^2)는 전체제곱합에서 회귀제곱합의 비율 : SSR/SST
0<=R^2<=1, SST=SSR+SSE
결정계수(R^2)는 전체 데이터를 회귀모형이 설명할 수 있는 설명력을 의미
단순회귀분석에서 결정계수= 상관계수 𝛾^2

회귀직선의 적합도 검토

결정계수(R^2)을 통해 추정된 회귀식이 얼마나 타당한지 검토
(결정계수가 1에 가까울수록 회귀모형이 자료를 잘 설명)
독립변수가 종속변수 변동의 몇%를 설명하는지 나타내는 지표
다변량 회귀분석(다중선형회귀분석)에서는 독립변수의 수가 많아지면, 결정계수가 높아지므로 독립변수가 유의하든, 유의하지 않든 독립변수의 수가 많아지면 결정계수가 높아지는 단점O
-> 단점 보완을 위해 수정된 결정계수(Ra^2 : adjusted R^2)활용
수정된 결정계수
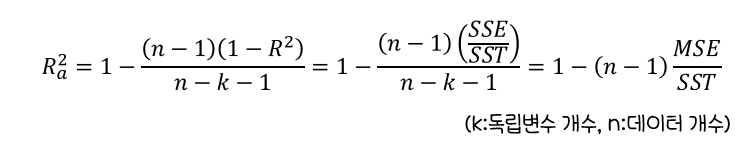
수정된 결정계수는 결정계수보다 작은 값으로 산출
MSE : 평균제곱 오차

*오차(Error)와 잔차(Residual)의 차이

오차 : 모집단에서 실제값이 회귀선과 비교해볼 때 나타나는 차이
(정확치와 관측치의 차이)
잔차: 표본에서 나온 관측값이 회귀선과 비교해 볼 때 나타나는 차이.
-> 회귀모형에서 오차항은 측정X로 잔차를 오차항의 관찰값으로 해석하여 오차항에 대한 가정들의 성립 여부 조사.

다중선형회귀분석

다중선형회귀분석(다변량회귀분석)

다중 회귀식
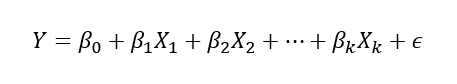
모형의 통계적 유의성

F-통계량(분산)으로 확인
유의수준 5% 이하에서 F-통계량의 p-값이 0.05보다 작으면 추정된 회귀식은 통계적으로 유의

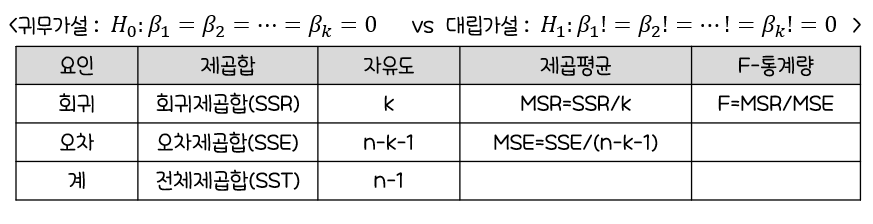
F-통계량이 크면 p-value가 0.05보다 작아지고 이렇게 되면 귀무가설을 기각. 즉, 모형이 유의

회귀계수의 유의성

단변량회귀분석(단순선형회귀분석)의 회귀계수 유의성 검토와 같이 t-통계량(평균)으로 확인
모든 회귀계수의 유의성이 통계적으로 검증되어야 선택된 변수들의 조합으로 모형 활용 가능

모형의 설명력

결정계수(R^2)나 수정된 결정계수(R^2) 확인

모형의 적합성

모형이 데이터를 잘 적합하고 있는지 잔차와 종속변수의 산점도로 확인

데이터가 전제하는 가정을 만족시키는가?

선형성, 독립성, 등분산성, 비상관성, 정상성

다중공선성(Multicollinearity)

다중회귀분석에서 설명변수(x) 사이에 선형관계가 존재하면 회귀계수의 정확한 추정 곤란
다중공선성 검사 방법
- 분산팽창요인(VIF) : 4보다 크면 다중공선성 존재, 10보다 크면 심각한 문제
- 상태지수 : 10이상이면 문제O, 30보다 크면 심각한 문제
  - 다중선형회귀분석에서 다중공선성의 문제가 발생하면, 문제가 있는 변수를 제거 or 주성분회귀, 능형회귀 모형을 적용하여 해결

회귀분석의 종류

단순회귀 : 독립변수가 1개, 종속변수와의 관계가 직선

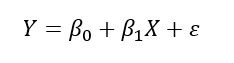
다중회귀 : 독립변수가 k개, 종속변수와의 관계가 선형(1차 함수)

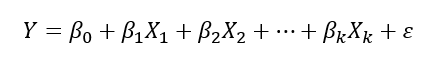
로지스틱 회귀 : 종속변수가 범주형(2진변수)
-단순 로지스틱 회귀/다중/다항 로지스틱 회귀
-exp=e^

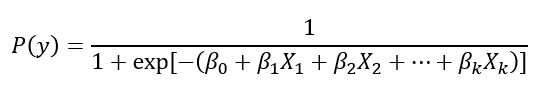
다항회귀 : 독립변수와 종속변수와의 관계가 1차함수 이상인 관계
-단, k=1이면 2차 함수 이상, k는 항의 수

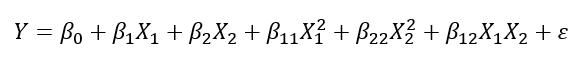
곡선회귀 : 독립변수가 1개, 종속변수와의 관계가 곡선
-2차 곡선인 경우

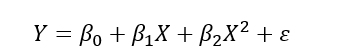
-3차 곡선인 경우

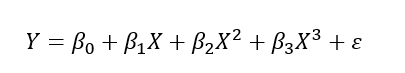
비선형 회귀 : 회귀식의 모양이 미지의 모수들의 선형관계로 이뤄져 있지 않은 모형

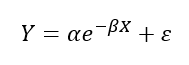
회귀분석 사례

R프로그램을 통한 회귀분석

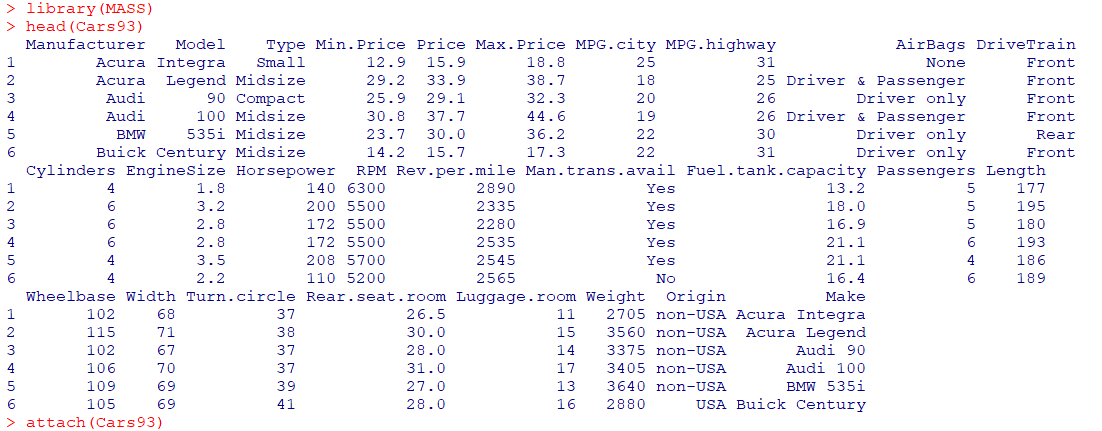
MASS 패키지의 Car93 데이터셋의 가격(Price)를 종속변수(y)로 선정하고 엔진 크기(Engine-Size), RPM, 무게(Weight)를 이용해서 다중회귀분석 실시

library(MASS)
head(Cars93)
attach(Cars93)	#데이터를 R 검색경로에 추가해 변수명으로 바로 접근 가능
lm(Price~EngineSize+RPM+Weight, data=Cars93)  #lm 선형회귀분석
summary(lm(Price~EngineSize+RPM+Weight, data=Cars93))

결과 및 해석

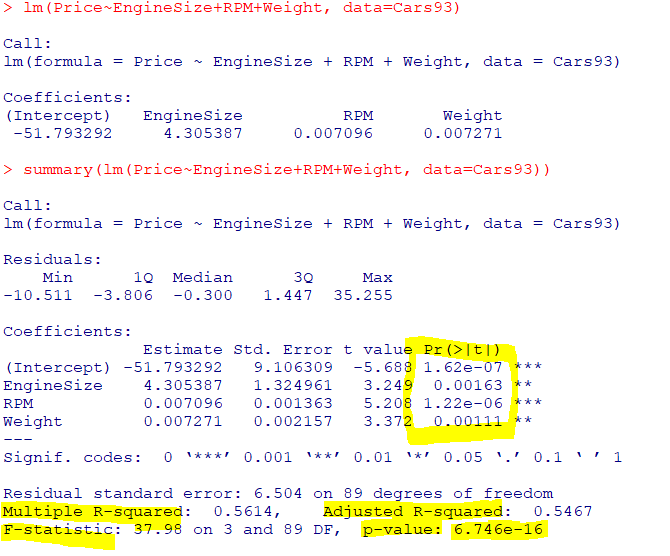
F-통계량 : 37.98, p-value(유의확률) : 6.746e-16
-> 유의수준 5%하에서 추정된 회귀모형이 통계적으로 매우 유의함
결정계수 : 0.5614 , 수정된 결정계수 : 0.5467
-> 조금 낮게 나타나 회귀식이 데이터를 적절하게 설명하고 있다곤 할 수 X
회귀계수들의 p-값이 0.05보다 작으므로 회귀계수의 추정치들이 통계적으로 유의
결정계수가 낮아 데이터 설명력은 낮으나, 회귀분석 결과에서 회귀식과 회귀계수들이 통계적으로 유의하여 자동차의 가격을 엔진의 크기,RPM,무게로 추정 가능

R프로그램을 통한 로지스틱 회귀분석

데이터 설명 : 림프절이 전립선 암에 대해 양성인지 여부를 예측하는 데이터

변수명	설명
양성여부(r)	전립선암에 대한 양성 여부
age	환자의 연령
stage	질병 단계 : 질병이 얼마나 진행되어 있는지 나타내는 척도
grade	종양의 등급 : 진행의 정도
xray	x-선 결과
acid	특정한 부위에 종양이 전이되었을 때 상승되는 혈청의 인산염값

분석 결과

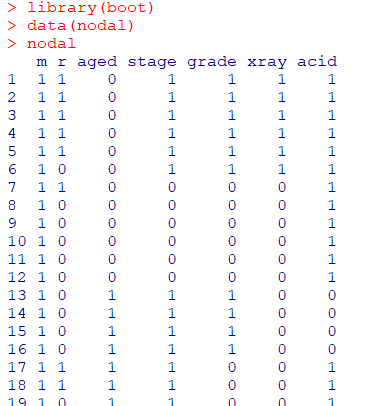
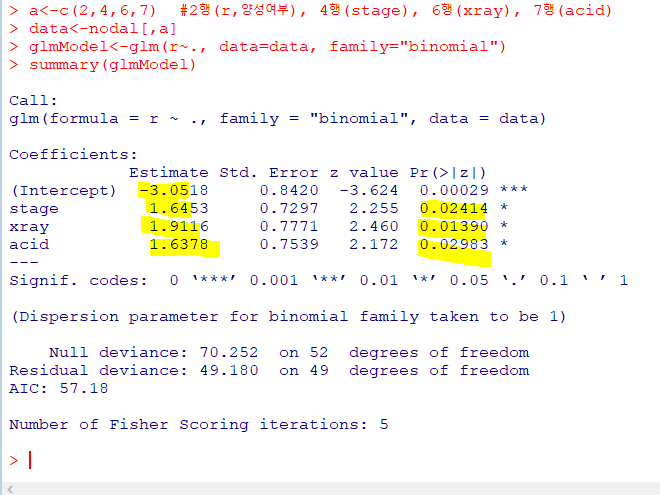
glm : 로지스틱 회귀분석
2번째 변수인 양성여부(r)를 종속변수(y)로 두고, 5개의 변수를 독립변수(x)로 하여 로지스틱 회귀분석 실시
age와 grade는 유의수준 5%하에서 유의X로 이를 제외한 3개의 변수(stage, xray, acid)를 활용해 모형 개발
stage, xray, acid의 추정계수는 유의수준 5%하에서 유의하게 나타나므로
p(r=1)=1/(1+exp-(-3.05+1.65stage+1.91xray+1.64acid))의 선형식 가능

최적회귀방정식

최적회귀방정식의 선택

설명변수(x) 선택
: 필요한 변수만 상황에 따라 타협을 통해 선택

y에 영향을 미칠 수 있는 모든 설명변수 x들을 y의 값을 예측하는 데 참여
데이터에 설명변수 x들의 수가 많아지면 관리하는데 많은 노력이 요구되므로, 가능한 범위 내에서 적은 수의 설명변수 포함

모형선택(Exploratory Analysis)
: 분석 데이터에 가장 잘 맞는 모형을 찾아내는 방법

모든 가능한 조합의 회귀분석(All Possible Regression) : 모든 가능한 독립변수들의 조합에 대한 회귀모형을 생성한 뒤 가장 적합한 회귀모형 선택

단계적 변수선택(Stepwise Variable Selection)

전진선택법(Forward Selection) : 절편만 있는 상수모형으로부터 시작해 중요하다고 생각되는 설명변수부터 차례로 모형에 추가
-변수의 개수가 많은 경우에도 사용 가능
-변수값의 작은 변동에도 그 결과가 크게 달라짐 =>안정성 부족
후진제거법(Backward Elimination) : 독립변수 후보 모두를 포함한 모형에서 출발해 가장 적은 영향을 주는 변수부터 하나씩 제거하면서 더 이상 제거할 변수가 없을 때의 모형 선택
-변수의 개수가 많은 경우 사용하기 어려움
-전체 변수들의 정보를 이용
단계선택법(Stepwise Method) : 전진선택법에 의해 변수를 추가하면서 새롭게 추가된 변수에 기인해 기존 변수의 중요도가 약화되면 해당 변수를 제거하는 등 단계별로 추가 또는 제거되는 변수의 여부를 검토해 더 이상 없을 때 중단

벌점화된 선택기준
: 모형의 복잡도에 벌점을 주는 방법

방법

AIC(Akaike Information Criterion)

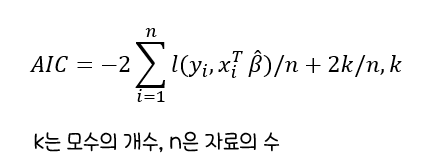
BIC(Bayesian Information Criterion)

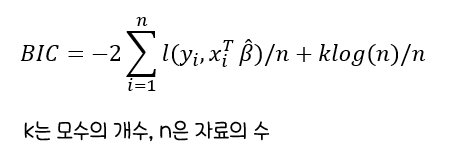
설명

모든 후보 모형들에 대해 AIC 또는 BIC를 계산하고, 그 값이 최소가 되는 모형을 선택
모형선택의 일치성(Consistency Inselection)
: 자료의 수가 늘어날 때 참인 모형이 주어진 모형 선택 기준의 최소값을 갖게 되는 성질
AIC는 일치성 성립X, BIC는 주요 분포에서 성립
AIC활용이 보편화된 방법
그 외의 벌점화 선택기준 : RIC(Risk Inflation Criterion), CIC(Covariance Inflation Criterion), DIC(Deviation Information Criterion)

최적회귀방정식의 사례

변수 선택법 예제(유의확률 기반)

x1, x2, x3, x4를 독립변수로 가지고 y를 종속변수로 가지는 선형회귀모형을 생성한 뒤, step()함수를 이용하지 않고 직접 후진제거법을 적용하는 R코드 작성

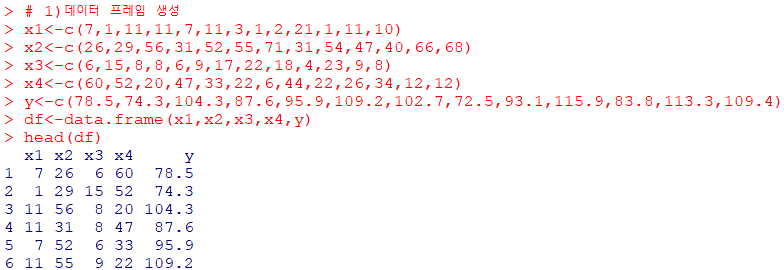
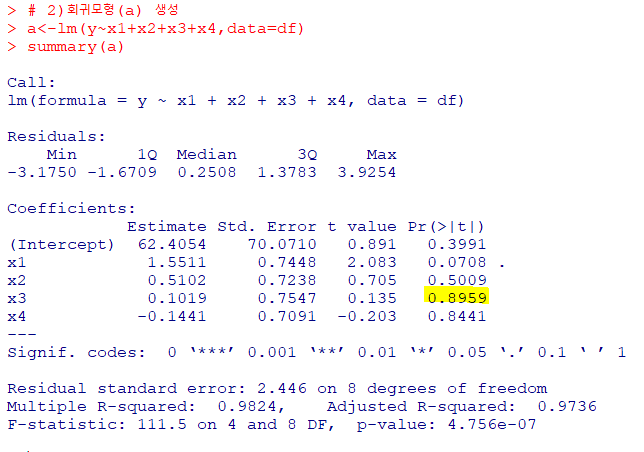
summary(a)에서 모형의 유의성을 판단
: F-통계량을 확인한 결과 111.5이며, p-value가 4.756e-07임으로 통계적으로 유의
각각의 입력변수들의 통계적 유의성 검토
: t-통계량을 통한 유의확률이 0.05보다 작은 변수가 하나도 존재하지 않아 모형을 활용할 수 없다고 판단
-> 유의확률이 가장 높은 x3을 제외하고 다시 회귀모형 생성

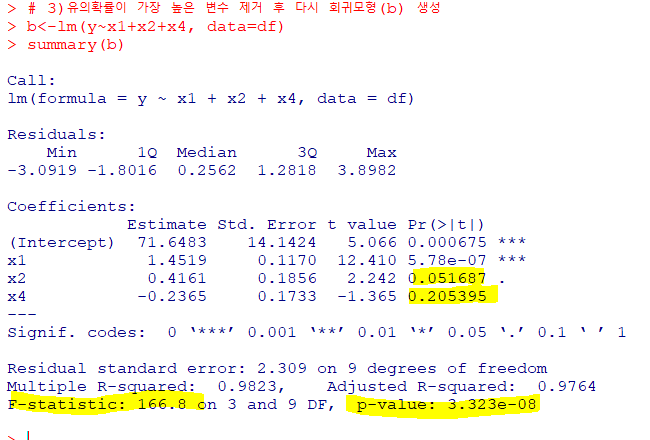
x3변수 제거 후, 모형의 유의성 : F-통계량에 대한 유의확률은 통계적으로 유의
x1을 제외한 2개의 변수의 유의확률이 0.05보다 높게나타나 유의하지 않음
-> 유의확률이 가장 높은 x4 변수를 제외하고 회귀모형 다시 생성

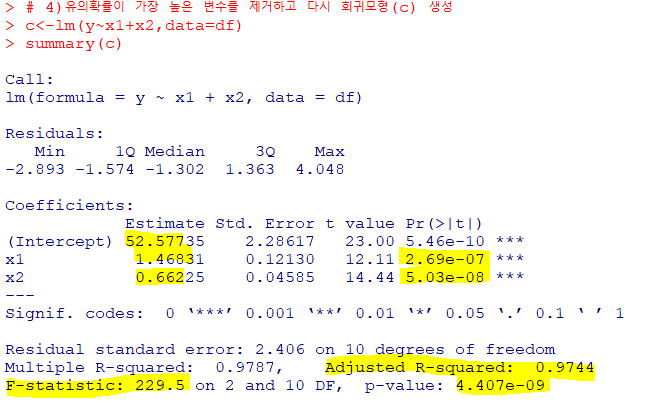
F-통계량을 통해 유의수준 0.05하에서 모형이 통계적으로 유의미
다변량회귀분석에 선정된 x1, x2변수에 대한 각각의 유의확률 값이 모두 통계적으로 유의
수정된 결정계수는 0.9744로 선정된 다변량회귀식이 전체 데이터의 97.44%를 설명하고 있는 것을 확인
후진제거법을 통해 최종적으로 얻게 된 추정된 회귀식
: y=52.57735+1.436831x1+0.66225x2

*부동소수점(Floating Point) : 컴퓨터에서 실수를 표시하는 방법
-(가수)(밑수)^(지수)로 표현
-가수: 유효숫자
-지수:소숫점 위치

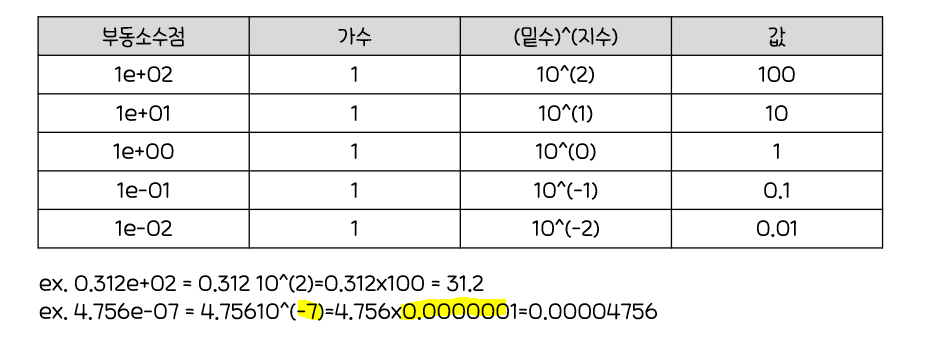
변수 선택법 예제(벌점화 전진선택법)

step함수를 사용하여 전진선택법을 적용하여 변수 제거를 수행해보자.

step(lm(출력변수~입력변수, 데이터셋), scope=list(lower=~1, upper=~입력변수)
, direction="변수선택방법")

#scope:변수선택과정에서 설정할 수 있는 가장 큰 모형/가장 작은 모형
#scope가 없는 경우
전진선택법 : 현재 선택한 모형을 가장 큰 모형으로,
후진제거법 : 상수항만 있는 모형을 가장 작은 모형으로 설정

#direction
forward : 전진선택법, backward : 후진제거법, stepwise : 단계선택법

#k : 모형선택 기준에서 AIC, BIC와 같은 옵션 사용
k=2이면 AIC, k=log(자료의 수)이면 BIC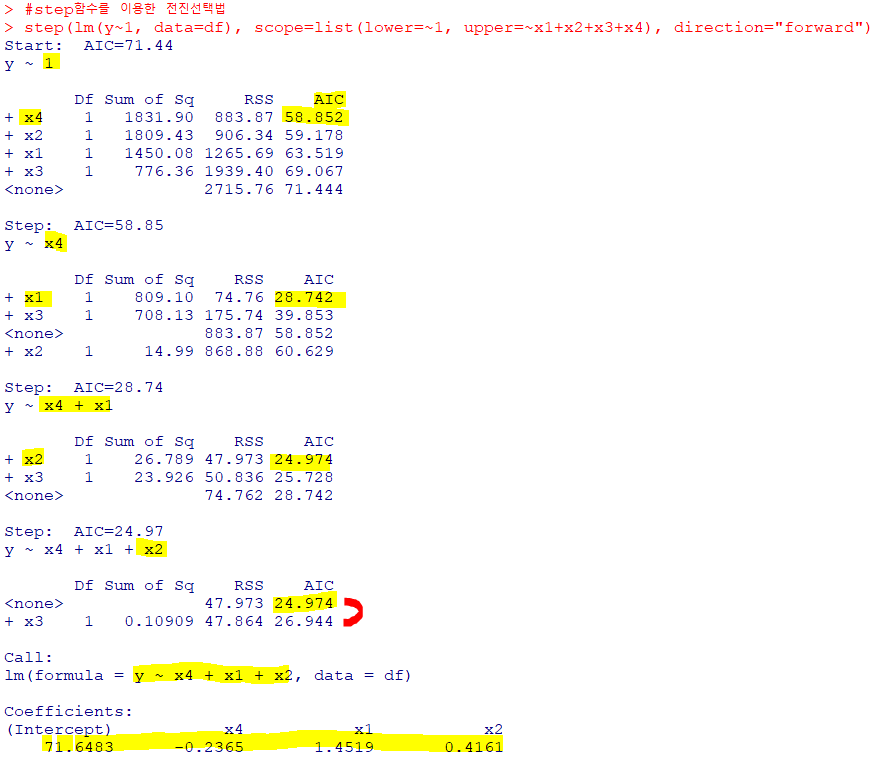

벌점화 방식을 적용한 전진선택법 실시 결과, 가장 먼저 선택된 변수는 AIC값이 58.852로 가장 낮은 x4
x4에 x1을 추가 했을 때, AIC값이 28.742가 되고 x2를 추가했을 때 AIC값이 24.974로 최소화
-> 더 이상 AIC를 낮출 수 없어 변수 선택 종료
최종적으로 선택된 추정된 회귀식
: y=71.6483-0.2365x4+1.4519x1+0.4161x2

변수 선택법 예제(벌점화 후진제거법)

활용데이터
-전립선암 자료(8개의 입력변수와 1개의 출력변수)
-마지막 열(train)에 있는 변수는 학습자료인지 예측자료인지를 나타내는 변수로 이번 분석에서 사용X

변수명	설명
lcavol	종양 부피의 로그
lweight	전립선 무게의 로그
age	환자의 연령
lbph	양성 전립선 증식량의 로그
svi	암이 정낭을 침범할 확률
lcp	capsular penetration의 로그 값
gleason	Gleason 점수
pgg45	Gleason 점수가 4 또는 5 인 비율
lpsa	전립선 수치의 로그

library(ElemStatLearn)
Data=prostate
data.use=Data[,-ncol(Data)]
lm.full.Model=lm(lpsa~.,data=data.use)

후진제거법에서 AIC를 이용한 변수선택

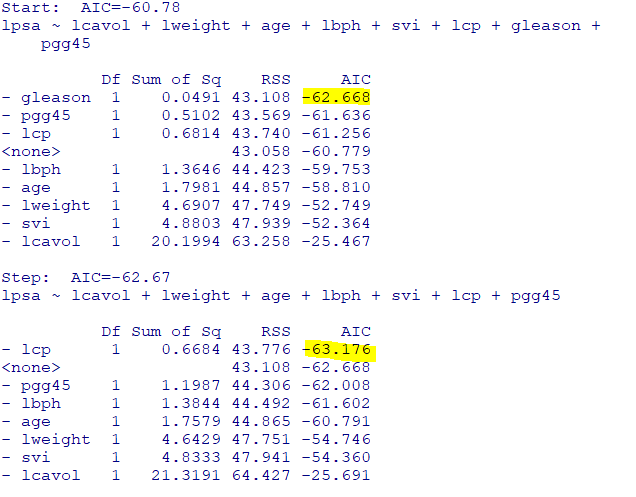
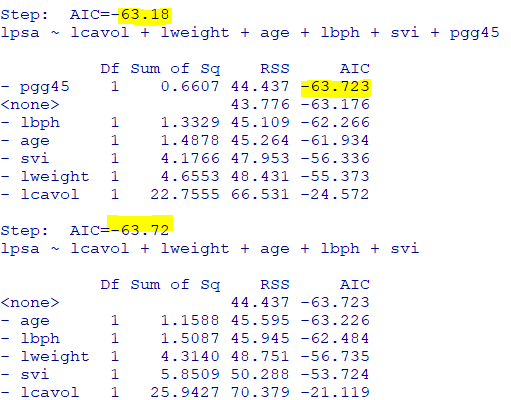
-맨 처음 AIC는 -62.67로 gleason을 제거하고 회귀분석 실시
-차례로 lcp, pgg45 순서로 제거되어 회귀분석 실시
-Step : AIC=~에 적혀있는 AIC보다 작으면(절대값 기준 크면) 삭제

🕑시계열 분석

시계열 자료

시간의 흐름에 따라 관찰된 값
시계열 데이터 분석을 통해 미래의 값을 예측하고 경향, 주기, 계절성 등을 파악하여 활용

시계열 자료의 종류

비정상성 시계열 자료
: 시계열 분석을 실시할 때 다루기 어려운 자료.
-대부분의 시계열 자료
정상성 시계열 자료
: 비정상 시계열을 핸들링해 다루기 쉬운 시계열 자료로 변환한 자료

정상성

평균이 일정할 경우

모든 시점에 대해 일정한 평균
평균이 일정하지 않은 시계열은 차분(Difference)를 통해 정상화

*차분
: 현시점 자료-전 시점 자료
-일반차분(Regular Difference) : 바로 전 시점의 자료를 빼는 방법
-계절차분(Seasonal Difference) : 여러 시점 전의 자료를 빼는 방법.
=> 계절성을 갖는 자료를 정상화하는데 사용

분산이 일정

분산도 시점에 의존하지 않고 일정
분산이 일정하지 않을 경우 변환(Transformation)을 통해 정상화

공분산(두 확률변수의 방향의 조합)도 단지 시차에만 의존, 실제 특정 시점 t, s에는 의존x

정상 시계열의 모습

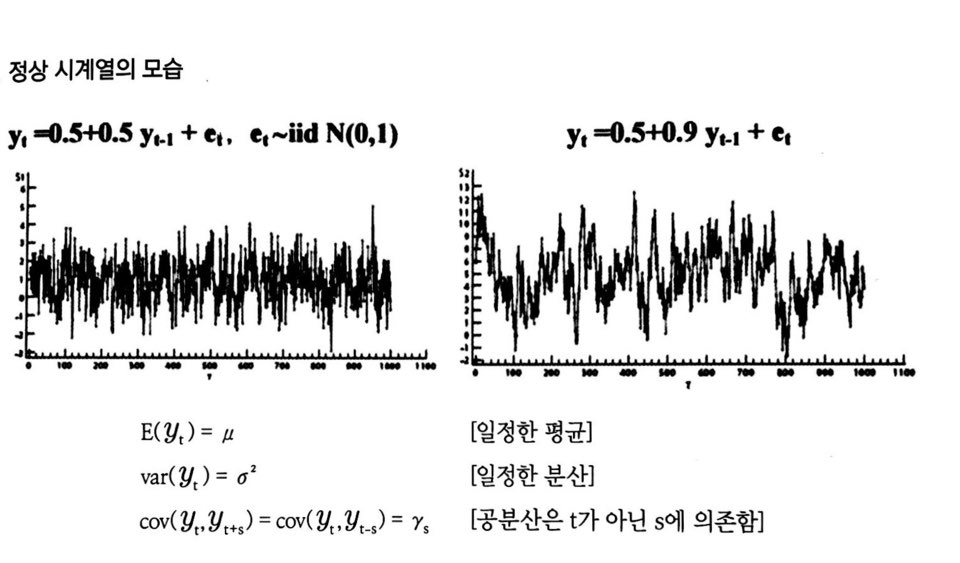
정상 시계열의 특징

정상 시계열은 어떤 시점에서 평균과 분산 그리고 특정한 시차의 길이를 갖는 자기공분산을 측정하더라도 동일한 값
정상 시계열은 항상 그 평균값으로 회귀하려는 경향이 있으며, 그 평균값 주변에서의 변동은 대체로 일정한 폭
정상 시계열이 아닌 경우 특정 기간의 시계열 자료로부터 얻은 정보를 다른 시기로 일반화 불가능

시계열자료 분석방법

분석방법
: 회귀분석(계량경제)방법, Box-Jenkins 방법, 지수평활법, 시계열 분해법 등

자료 형태에 따른 분석방법

일변량 시계열분석
: Box-Jenkins(ARMA), 지수 평활법, 시계열 분해법 등
-시간(t)를 설명변수(x)로 한 회귀모형주가, 소매물가지수 등 하나의 변수에 관심을 갖는 경우의 시계열 분석
다중 시계열분석
: 계량경제 모형(회귀분석방법), 전이함수 모형, 개입분석, 상태공간 분석, 다변량 ARIMA 등
-여러 개의 시간(t)에 따른 변수들을 활용하는 시계열 분석
-계량경제 : 시계열 데이터에 대한 회귀분석(ex. 이자율, 인플레이션이 환율에 미치는 요인)

이동평균법

과거로부터 현재까지의 시계열 자료를 대상으로 일정 기간별 이동평균을 계산하고, 이들의 추세를 파악하여 다음 기간을 예측
시계열 자료에서 계절변동과 불규칙 변동을 제거
-> 추세변동과 순환변동만 가진 시계열로 변환하는 방법
n개의 시계열 데이터를 m기간으로 이동평균하면 n-m+1개의 이동평균 데이터가 생성

이동평균법의 특징

간단하고 쉽게 미래 예측 가능
자료의 수가 많고 안정된 패턴을 보이는 경우 예측의 품질(Quality)이 높음
특정 기간 안에 속하는 시계열에 대해서는 동일한 가중치 부여
일반적으로 시계열 자료에 뚜렷한 추세가 있거나 불규칙변동이 심하지 않은 경우에는 짧은 기간(m개수 적음)의 평균 사용
불규칙 변동이 심한 경우 긴 기간(m의 개수가 많음)의 평균을 사용
가장 중요한 것은 적절한 기간을 사용하는 것
-> 적절한 m의 개수를 결정하는 것

지수평활법

일정 기간의 평균을 이용하는 이동평균법과는 달리
모든 시계열 자료를 사용하여 평균을 구하며, 시간의 흐름에 따라 최근 시계열에 더 많은 가중치를 부여하여 미래 예측

지수평활법의 특징

단기간에 발생하는 불규칙 변동을 평활
자료의 수가 많고, 안정된 패턴을 보이는 경우일수록 예측 품질 높음
지수평활법에서 가중치의 역할을 하는 것은 지수평활계수(α)
불규칙변동이 큰 시계열의 경우 지수평활계수(가중치)는 작은 값,
불규칙변동이 작은 시계열의 경우 큰 값의 지수평활계수(가중치)를 적용
(일반적으로, 0.05<=α<=0.3)
지수평활계수는 예측오차(실제 관측치와 예측치 사이의 잔차 제곱합,SSE)를 비교하여 예측오차가 가장 작은 값을 선택
지수평활계수는 과거로 갈수록 지속적으로 감소
지수평활법은 불규칙변동의 영향을 제거하는 효과가 있음
중기 예측 이상에 주로 사용
(단, 단순지수 평활법의 경우, 장기추세나 계절변동이 포함된 시계열 예측에는 적합x)

시계열모형

자기회귀 모형(AR모형, Autoregressive Model)
: p시점 전의 자료가 현재 자료에 영향을 주는 모형

AR(1) 모형 : 직전 시점 데이터로만 분석
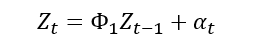
AR(2) 모형 : 연속된 2시점 정도의 데이터로 분석
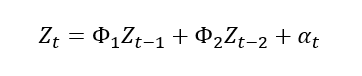
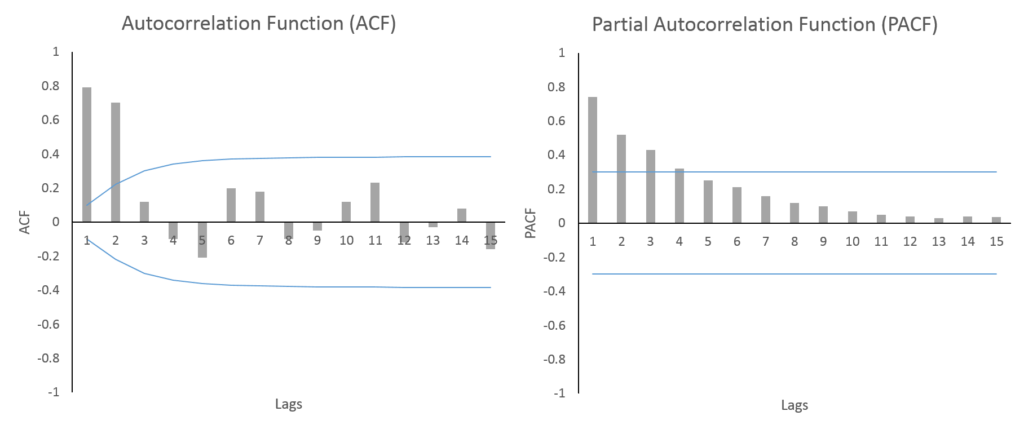
자기상관함수(ACF)는 빠르게 감소
부분자기함수(편자기상관함수)(PACF)는 어느 시점에서 절단점을 가짐
ACF가 빠르게 감소하고, PACF가 3시점에서 절단점을 갖는 그래프가 있다면, 2시점 전의 자료까지가 현재에 영향을 미치는 AR(2)모형

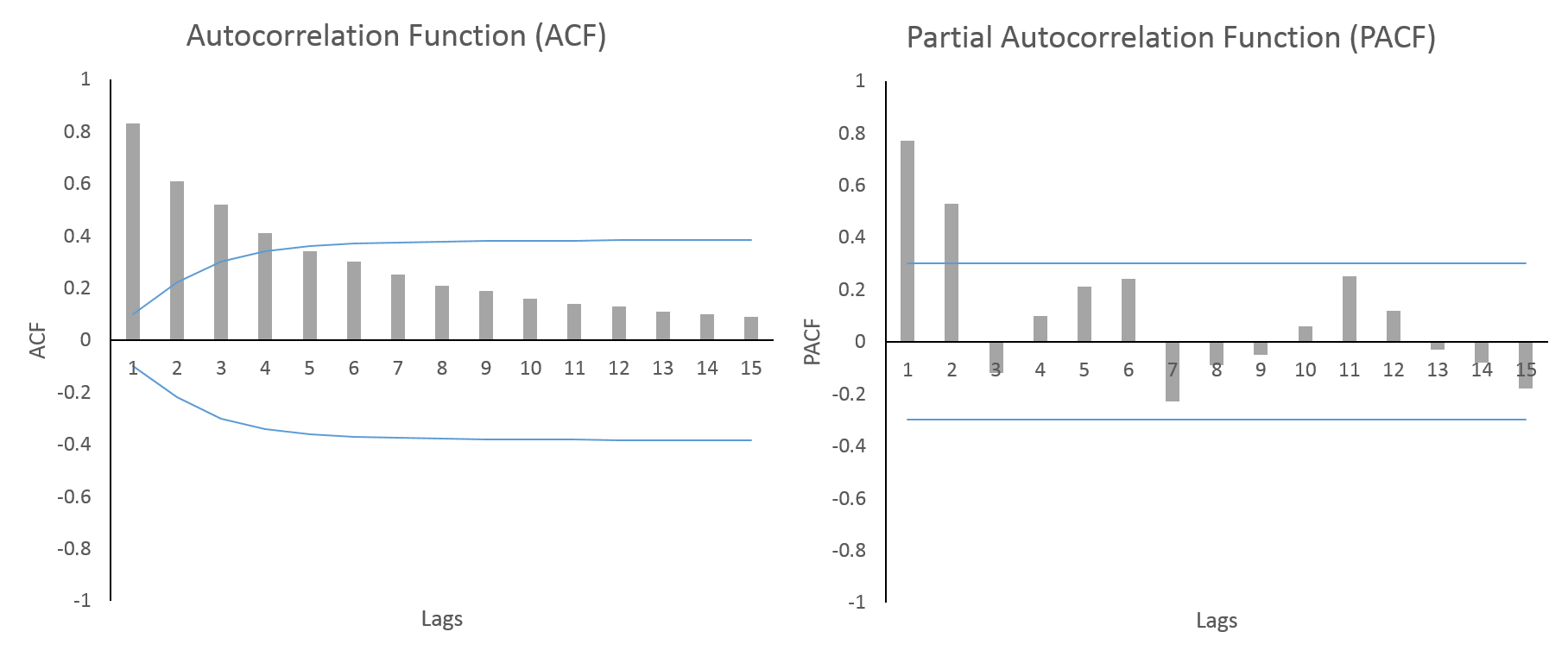
*자기상관계수와 부분자기상관계수

이동평균 모형(MA모형, Moving Average Model)
: 유한한 개수의 백색잡음의 결합이므로 언제나 정상성 만족

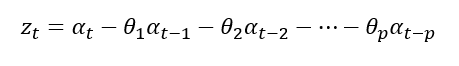
1차 이동평균모형(MA(1) 모형) : 이동평균모형 중 가장 간단한 모형
-시계열이 같은 시점의 백색잡음과 바로 전 시점의 백색잡음의 결합
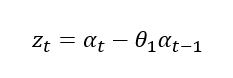
2차 이동평균모형(MA(2) 모형) : 바로 전 시점의 백색잡음과 시차가 2인 백색잡음의 결합으로 이뤄진 모형
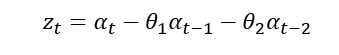
AR모형과 반대로 ACF에서 절단점을 갖고, PACF가 빠르게 감소

자기회귀누적이동평균 모형(ARIMA(p,d,q) 모형, Autoregressive Integrated Moving Average Model)

비정상시계열 모형
차분이나 변환을 통해 AR모형이나 MA모형, 이 둘을 합친 ARMA모형으로 정상화 가능
p는 AR모형
q는 MA모형과 관련이 있는 차수
시계열 {Zt}의 d번 차분한 시계열이 ARMA(p,q) 모형이면,
시계열 {Zt}는 차수가 p,d,q인 ARIMA모형, 즉 ARIMA(p,d,q)모형을 갖는다
d=0 : ARMA(p,q)모형, 정상성 만족
(ARMA(0,0)일 경우 정상화 불필요)
p=0 : IMA(d,q)모형, d번 차분하면 MA(q)모형 따름
q=0 : ARI(p,d)모형, d번 차분하면 AR(p)모형 따름

ARIMA(0,1,1)	#1차분 후 MA(1) 활용
ARIMA(1,1,0)	#1차분 후 AR(1) 활용
ARIMA(1,1,2)	#1차분 후 AR(1), MA(2), ARMA(1,2) 선택
->가장 간단한 모형을 선택하거나 AIC를 적용하여 점수가 가장 낮은 모형 선정

*자기회귀이동평균(Autoregressive and Moving Average, ARMA) 모형
: 자기회귀와 이동평균 다항식으로, 약한 정상성을 가진 확률적 시계열을 표현하는데 사용.
-ARMA(p,q)로 표기(p는 자기회귀 다항식 차수, q는 이동평균 다항식 차수)

분해 시계열
: 시계열에 영향을 주는 일반적인 요인을 시계열에서 분리해 분석하는 방법

회귀분석적인 방법 주로 사용
분해식의 일반적 정의

R을 이용한 시계열분석

영국 왕들의 사망 시 나이 데이터를 이용한 시계열분석
영국 왕 42명의 사망시 나이 예제는 비계절성을 띄는 시계열 자료
비계절성을 띄는 시계열 자료는 트렌드 요소(추세요인), 불규칙 요소로 구성
20번째 왕 까지는 38세~55까지 수명 유지, 그 이후부터 수명이 늘어 40번째 왕은 73세까지 생존

분해 시계열

자료 읽기 및 그래프 그리기

library(tseries)	#시계열 분석 및 전산 금융
library(forecast)	#시계열 및 선형 모델에 대한 예측 함수
library(TTR)		#기술 거래 규칙
king<-scan("http://robjhyndman.com/tsdldata/misc/kings.dat",skip=3)
#skip=3은 3번째 열 건너뜀, scan()은 입력함수

king.ts<-ts(king)	#ts()는 시계열 데이터 생성
plot.ts(king.ts)

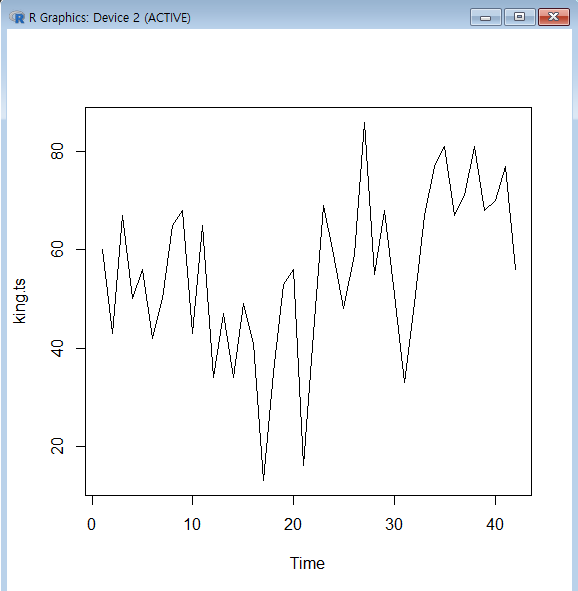
3년마다 평균을 내서 그래프를 부드럽게 표현

king.sma3<-SMA(king.ts,n=3)		#SMA : 이동평균
plot.ts(king.sma3)

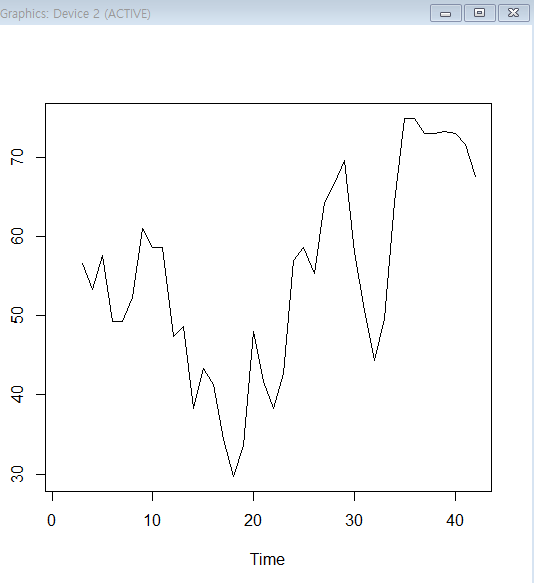
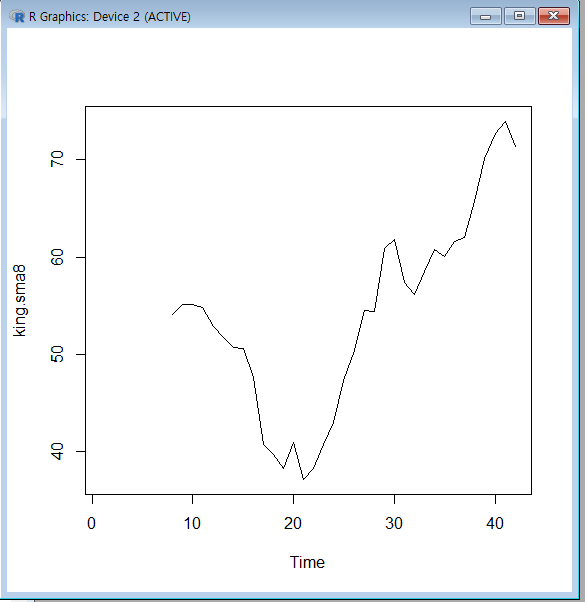
8년마다 평균을 내서 그래프를 부드럽게 표현

king.sma8<-SMA(king.ts,n=8)		#SMA : 이동평균
plot.ts(king.sma8)

ARIMA 모델
-ARIMA모델은 정상성 시계열에 한해 사용
-비정상 시계열 자료는 차분해 정상성을 만족하는 조건의 시계열로 변경
-이전 그래프에서 평균이 시간에 따라 일정치 않은 모습을 보이므로 비정상시계열=>차분 진행

diff(data, differences=차분횟수)

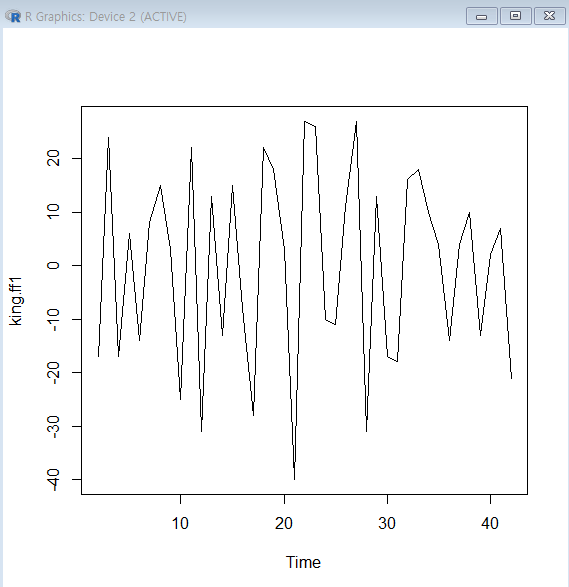
-1차 차분 결과에서 평균과 분산이 시간에 따라 의존하지 않음을 확인
-ARIMA(p,1,q)모델이며 차분을 1번해야 정상성 만족

ACF와 PACF를 통한 적합한 ARIMA 모델 결정
-ACF
- lag는 0부터 값을 갖는데, 너무 많은 구간을 설정하면 그래프를 보고 판단 어려움
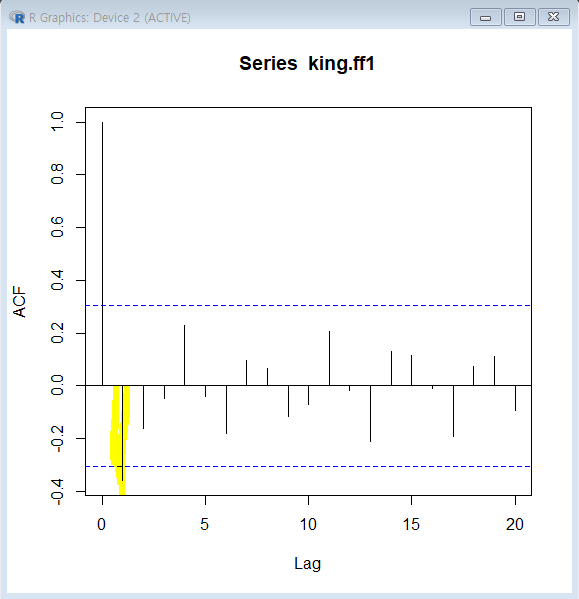
- ACF값이 lag 1인 지점 빼고 모두 점선 구간 안
-PACF
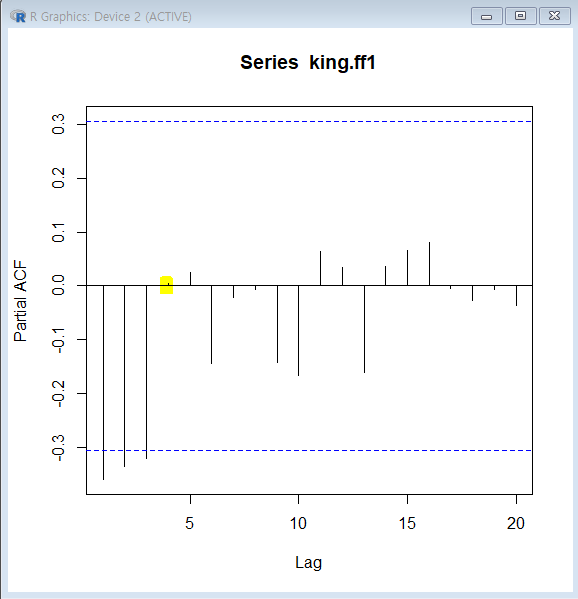
- PACF값이 lag 1, 2, 3에서 점선 구간을 초과하고 음의 값을 가지며 절단점은 lag 4

종합
-ARMA 후보들이 생성
- ARMA(3,0)모델 : PACF값이 lag4에서 절단점을 가짐. AR(3)
- ARMA(0,1)모델 : ACF값이 lag2에서 절단점을 가짐. MA(1)
- ARMA(p,q)모델 : AR모형+MA모형

적절한 ARIMA 모형 찾기
-forecast패키지에 내장된 auto.arima()함수 이용
-auto.arima() : 데이터를 활용하여 최적의 ARIMA 모형 선택

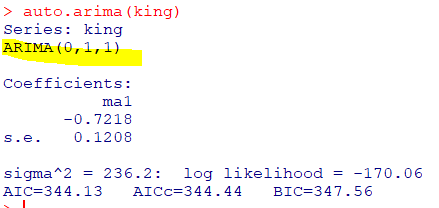
-영국 왕 사망 나이 데이터의 적절한 ARIMA 모형은 ARIMA(0,1,1)

예측

king.arima<-arima(king,order=c(0,1,1))
#선정된 ARIMA 모형으로 데이터 보정(fitting)

king.forecasts<-forecast(king.arima)
#시계열 모델을 입력받아 적절한 예측치를 냄

king.forecasts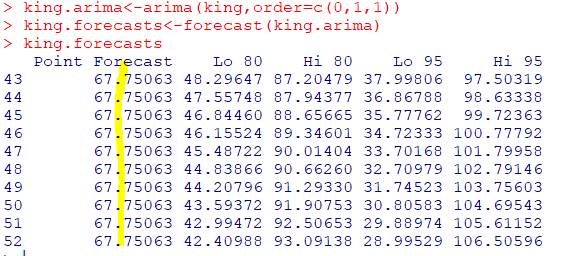

-42명의 영국왕 중에서 마지막 왕의 사망시 나이는 56세
-43번째에서 52번째 왕 까지의 10명의 왕의 사망시 나이를 예측한 결과 67.75살로 추정
-5명 정도만 예측하고 싶다면, 옵션에 h=5 입력(forecast에)
-신뢰 구간은 80%~90% 사이

🔏다차원척도법

다차원척도법(Multidimensional Scaling/MDS)

객체간 근접성(Proximity)을 시각화하는 통계기법
군집분석과 같이 객체들을 대상으로 변수를 측정한 후, 개체들 사이의 유사성/비유사성을 측정하여 개체들을 2차원 공간상에 점으로 표현하는 분석 방법
개체들을 2차원 또는 3차원 공간상에 점으로 표현하여 개체들 사이의 집단화를 시각적으로 표현

다차원척도법 목적

데이터 속에 잠재해 있는 패턴(Pattern), 구조를 찾아냄
그 구조를 소수 차원의 공간에 기하학적으로 표현
데이터 축소(Data Reduction)의 목적으로 다차원척도법 이용
-> 데이터에 포함되는 정보를 끄집어내기 위해서 다차원척도법을 탐색수단으로써 사용
다차원척도법에 의해서 얻은 결과를 데이터가 만들어진 현상이나 과정에 고유의 구조로서 의미 부여

다차원척도법 방법

개체들의 거리 계산 : 유클리드 거리행렬 활용
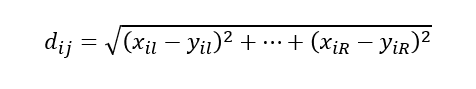
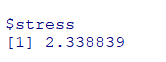
관측대상들의 상대적 거리의 정확도를 높이기 위해 적합 정도를 스트레스 값(Stress Value)로 나타냄
개체들을 공간상에 표현하기 위한 방법
: 부적합도 기준으로 Stress나 S-Stress를 사용
최적모형의 적합은 부적합도를 최소로 하는 반복 알고리즘을 이용.
이 값이 일정 수준 이하가 될 때 최종적으로 적합된 모형으로 제시
스트레스 값
Stree와 적합도 수준 M은 개체들을 공간상에 표현하기 위한 방법으로 Stress나 S-Stress를 부적합도 기준으로 사용

Stress	적합도 수준
0	완벽(Perfect)
0.05 이내	매우 좋은(Excellent)
0.05~0.10	만족(Satisfactory)
0.10~0.15	보통(Acceptable, but Doubt)
0.15 이상	나쁨(Poor)

다차원척도법 종류

계량적 MDS(Metric MDS)
: 데이터가 구간척도나 비율척도인 경우 활용 (전통적인 다차원척도법)
-N개의 케이스에 대해서 p개의 특성변수가 있는 경우, 각 개체들간의 유클리드 거리행렬을 계산하고 개체들간의 비유사성 S(거리제곱 행렬의 선형함수)를 공간상에 표현

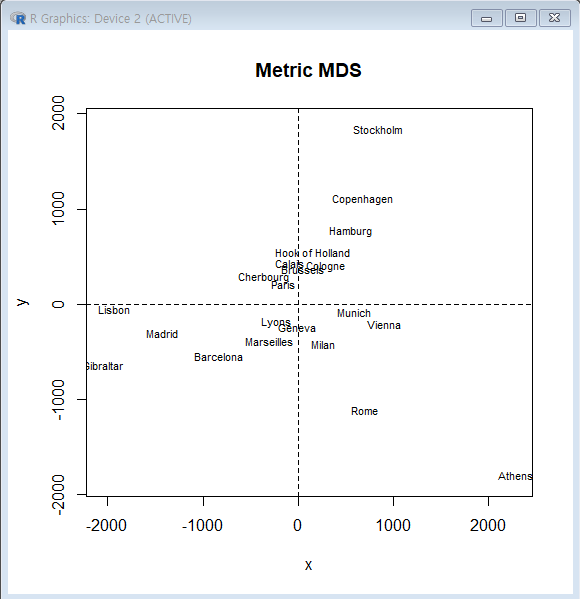
cmdscale 사례

MASS 패키지의 eurodist자료 이용
유럽 21개 도시들 사이의 거리 측정
cmdscale을 이용하여 2차원으로 21개의 도시들을 맵핑
종축은 북쪽 도시를 상단에 표시하기 위해 부호 변경

library(MASS)

#matrix 데이터 상의 값들을 거리로 생각하고 2차원상으로 나타냄
loc<-cmdscale(eurodist)

x<-loc[,1]
y<- -loc[,2]

#type="n" : 좌표를 찍지 않음, asp는 종횡의 비율
plot(x,y,type="n",asp=1,main="Metric MDS")

#cex=0.7 : 폰트 사이즈
text(x,y,rownames(loc),cex=0.7)

#v는 수직선 위치, h는 수평선 위치, lty는 선 유형(2:dashed), lwd는 선 두께
abline(v=0, h=0,lty=2,lwd=0.5)

비계량적 MDS(nonmetric MDS)
: 데이터가 순서척도인 경우 활용
-개체들 간의 거리가 순서로 주어진 경우에는 순서척도를 거리의 속성과 같도록 변환(Monotone Transformation) 하여 거리 생성 후 적용

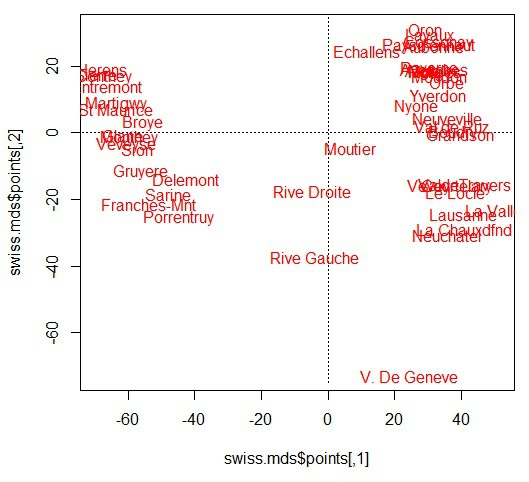
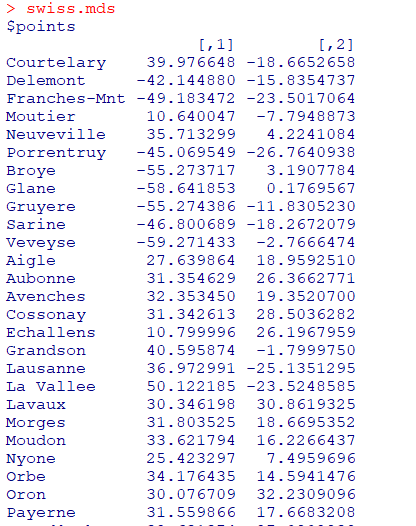
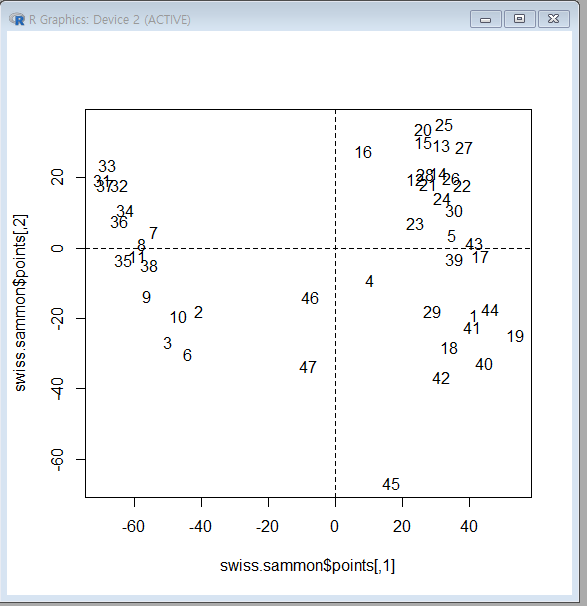
isoMDS 사례

MASS 패키지의 Swiss 자료를 이용하여 2차원으로 도시 맵핑
1888년경 스위스연방 중 47개의 불어권 주의 토양의 비옥도 지수와 여러 사회경제적 지표를 측정한 자료

library(MASS)
data(swiss)
swiss.x<-as.matrix(swiss[,-1])
swiss.dist<-dist(swiss.x) #유클리드 거리를 행렬 형태로 출력
swiss.mds<-isoMDS(swiss.dist)  #2차원상으로 cmdscale과 비슷
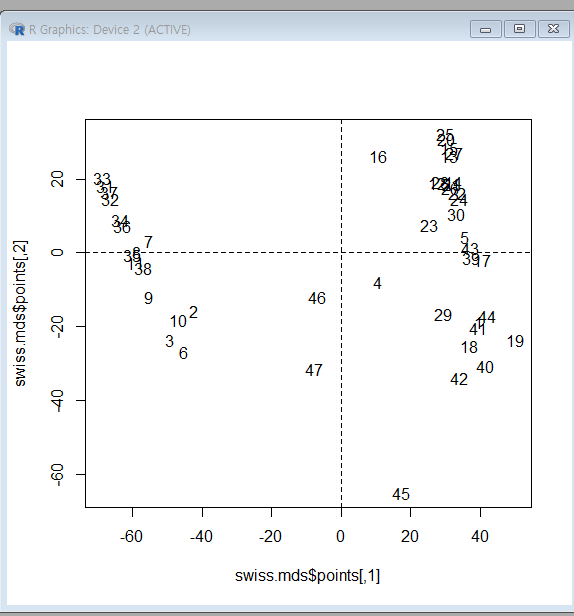
plot(swiss.mds$points, type="n")
text(swiss.mds$points, labels=as.character(1:nrow(swiss.x)))
abline(v=0, h=0, lty=2, lwd=0.5)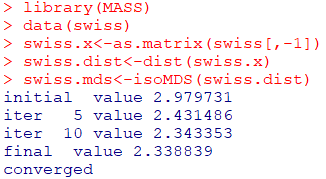

sammon 사례

swiss.x<-as.matrix(swiss[,-1])	#첫번째 열 제외
swiss.sammon<-sammon(dist(swiss.x))
plot(swiss.sammon$points, type="n")
text(swiss.sammon$points, labels=as.character(1:nrow(swiss.x)))
abline(v=0, h=0, lty=2, lwd=0.5)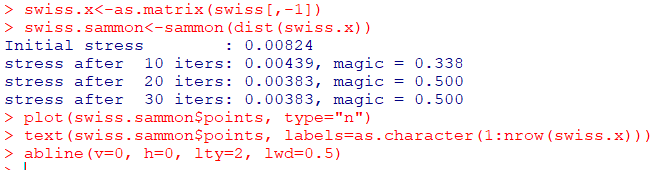

🎨주성분 분석

주성분분석(Principal Component Analysis)

여러 변수들의 변량을 주성분(Principal Component)이라는 서로 상관성이 높은 변수들의 선형 결합으로 만들어 기존의 상관성이 높은 변수들을 요약, 축소하는 기법
첫번째 주성분으로 전체 변동을 가장 많이 설명할 수 있도록 하고, 두 번째 주성분으로는 첫 번째 주성분과는 상관성이 없어서(낮아서) 첫 번째 주성분이 설명하지 못하는 나머지 변동을 정보의 손실 없이 가장 많이 설명할 수 있도록 변수들의 선형조합을 만듦

주성분분석의 목적

여러 변수들 간에 내재하는 상관관계, 연관성을 이용해
소수의 주성분으로 차원을 축소함으로써 데이터를 이해하기 쉽고 관리하기 쉽게 해줌
다중공선성이 존재하는 경우, 상관성이 없는(적은) 주성분으로 변수들을 축소하여 모형 개발에 활용
회귀분석 등의 모형 개발 시 입력변수들간 상관관계가 높은 다중공선성(Multicollinearity)이 존재할 경우 모형이 잘못 만들어져 문제 발생
연관성이 높은 변수를 주성분분석을 통해 차원을 축소한 후에 군집분석을 수행하면 군집화 결과와 연산속도를 개선 가능
기계에서 나오는 다수의 센서데이터를 주성분분석으로 차원을 축소한 후에 시계열로 분포나 추세의 변화를 분석하면 기계의 고장 징후를 사전에 파악하는데 활용

주성분분석 vs 요인분석

요인분석(Factor Analysis)

등간척도(또는 비율척도)로 측정한 두 개 이상의 변수들에 잠재되어 있는 공통인자를 찾아내는 기법

공통점

모두 데이터를 축소하는데 활용
원래 데이터를 활용해서 몇 개의 새로운 변수들을 만듦

차이점

생성된 변수의 수

요인분석 : 몇 개라고 지정 없이(2 or 3, 4, 5...) 만들기 가능
주성분분석 : 제1주성분, 제2주성분, 제3주성분 정도로 활용
(대개 4개 이상은 안넘음)

생성된 변수의 이름

요인분석 : 분석자가 요인의 이름을 명명
주성분분석 : 제1주성분, 제2주성분 등으로 표현

생성된 변수들 간의 관계

요인분석 : 새 변수들은 기본적으로 대등한 관계를 갖고 '어떤 것이 더 중요하다'라는 의미는 없음. 단, 분류/예측에 그다음 단계로 사용된다면 그 때 중요성 의미가 부여
주성분분석 : 제1주성분이 가장 중요하고, 그 다음 제2주성분이 중요

분석 방법의 의미

요인분석 : 목표변수를 고려하지 않고, 그냥 데이터가 주어지면 변수들을 비슷한 성격들로 묶어서 새로운 잠재변수를 만듦
주성분분석 : 목표 변수를 고려하여 목표 변수를 잘 예측/분류하기 위하여 원래 변수들의 선형 결합으로 이루어진 몇 개의 주성분들을 찾아냄

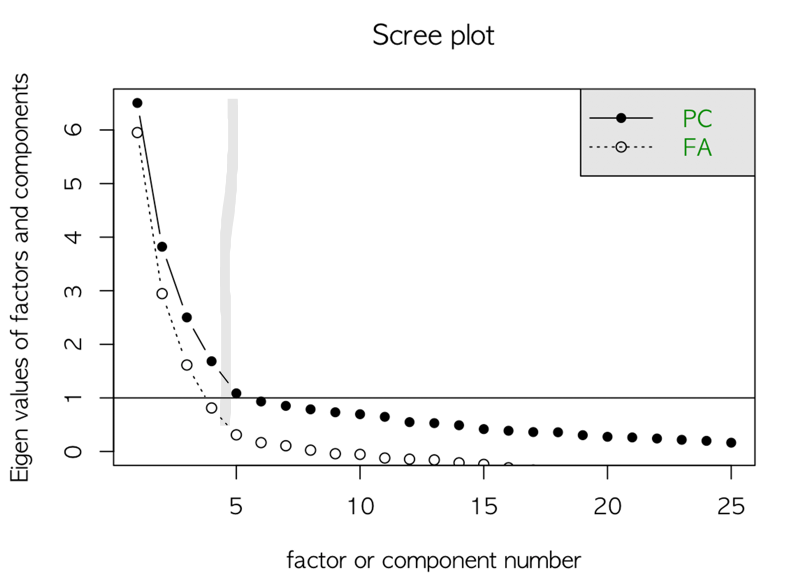
주성분의 선택법

주성분분석의 결과에서 누적기여율(Cumulative Proportion)이 85%이상이면 주성분의 수로 결정 가능

Scree Plot을 활용하여 고윳값(Eigenvalue)이 수평을 유지하기 전단계로 주성분의 수 선택

주성분 분석 사례

USArrests 자료

1973년 미국 50개주의 100,000명의 인구 당 체포된 세 가지 강력범죄수(Assault, Murder, Rape)와 각 주마다 도시에 거주하는 인구의 비율(%)로 구성
변수들 간의 척도의 차이가 상당히 크기 때문에 상관행렬을 사용하여 분석
특이치 분해(특이값 분해) : 행렬을 특정한 구조로 분해를 사용하는 경우 자료 행렬의 각 변수의 평균과 제곱의 합이 1로 표준화되었다고 가정

4개의 변수들 간 산점도

> library(datasets)
> data(USArrests)
> pairs(USArrests,panel=panel.smooth, main="USArrests data") # 산점도 행렬

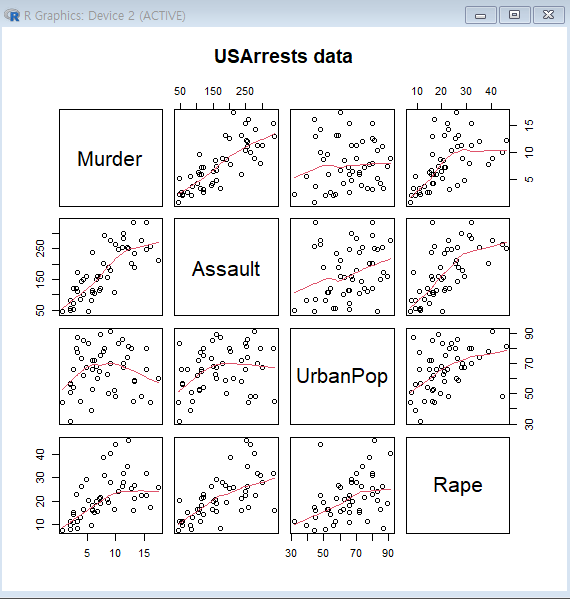
Murder과 UrbanPop 비율간의 관련성이 작아보임

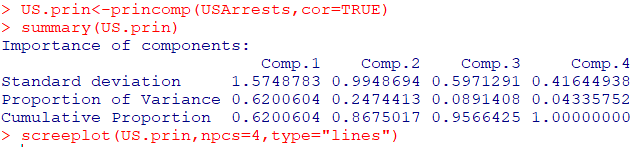
summary

#princomp : 주성분분석을 하는 함수. cor=TRUE면 상관행렬, F이면 공분산행렬
> US.prin<-princomp(USArrests,cor=TRUE)
> summary(US.prin)

#주성분을 x축, 주성분의 고유값(주성분의 분산)을 y축에 둔 그래프
> screeplot(US.prin,npcs=4,type="lines")

제1주성분과 제2주성분까지의 누적 분산비율은 대략 86.8%로 2개의 주성분 변수를 활용하여 전체 데이터의 86.8%를 설명가능
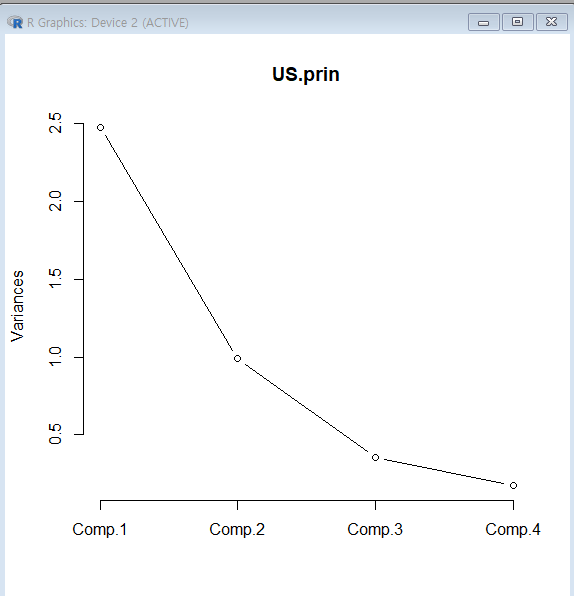
주성분들에 의해 설명되는 변동의 비율은 ScreePlot으로 확인

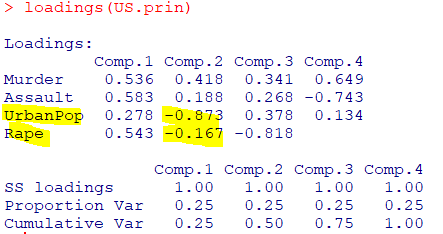
Loadings

네 개의 변수가 각 주성분 Comp.1-Comp.4까지 기여하는 가중치가 제시
제1주성분에는 네 개의 변수가 평균적으로 기여
제2주성분에는 (Murder,Assault)와 (UrbanPop, Rape)의 계수의 부호가 서로 다름

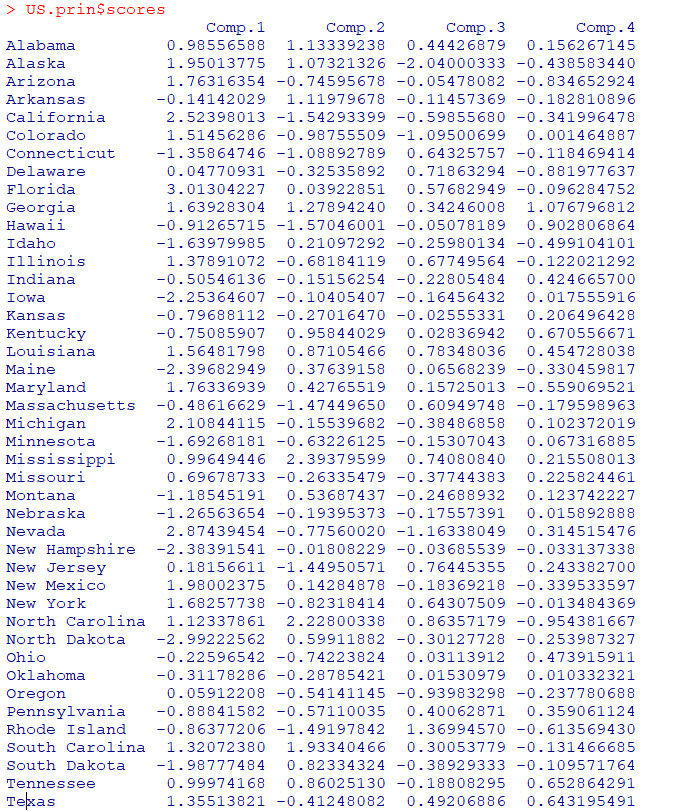
Scores

각 주성분 Comp.1-Comp.4의 선형식을 통해 각 지역(record)별로 얻은 결과 계산

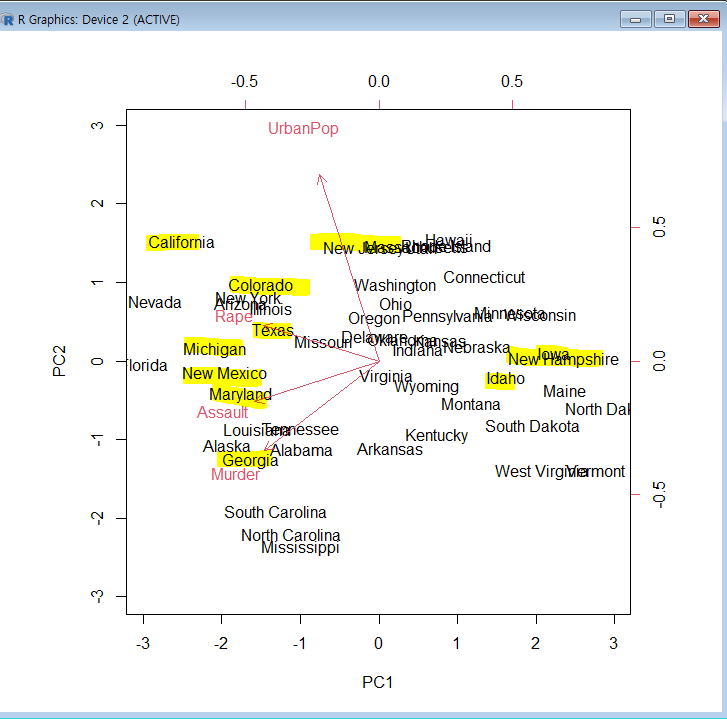
제 1-2주성분에 의한 행렬도

#자료행렬을 특이값 분해해 주성분분석을 실행하는 함수
#center=T : 데이터 중심이 0
#scale.=T : 데이터 표준화
> arrests.pca<-prcomp(USArrests, center=TRUE,scale.=TRUE)

#제 1,2 주성분에 의한 행렬도
> biplot(arrests.pca,scale=0)

조지아, 메릴랜드, 뉴 멕시코 등은 폭행과 살인의 비율이 상대적으로 높은 지역
미시간, 텍사스 등은 강간의 비율이 높은 지역
콜로라드, 캘리포니아, 뉴저지 등은 도시에 거주하는 인구의 비율이 높은 지역
아이다호, 뉴 햄프셔, 아이오와 등의 도시들은 도시에 거주하는 인구의 비율이 상대적으로 낮으면서 3대 강력범죄도 낮다

당당

MSSQL DBA 신입

이전 포스트

[ADsP] 데이터 마트

다음 포스트