[알고리즘] 탐색(Search) - DFS(Depth-First Search) & BFS(Breadth-First Search)

Kyung Jae, Cheong·2024년 10월 24일
Javapython알고리즘
0

알고리즘-Algorithms

목록 보기
10/15
post-thumbnail

본 시리즈는 프로그래밍 알고리즘의 개념을 정리하고 실습을 진행해보는 시리즈입니다.

  • 실습은 다음과 같은 개발환경 및 버전에서 진행하였습니다.
    • IDE : IntelliJ IDEA (Ultimate Edition)
    • Java : JDK 21 (corretto-21)
    • Python : 3.9 (conda env)

탐색(Search) - DFS & BFS

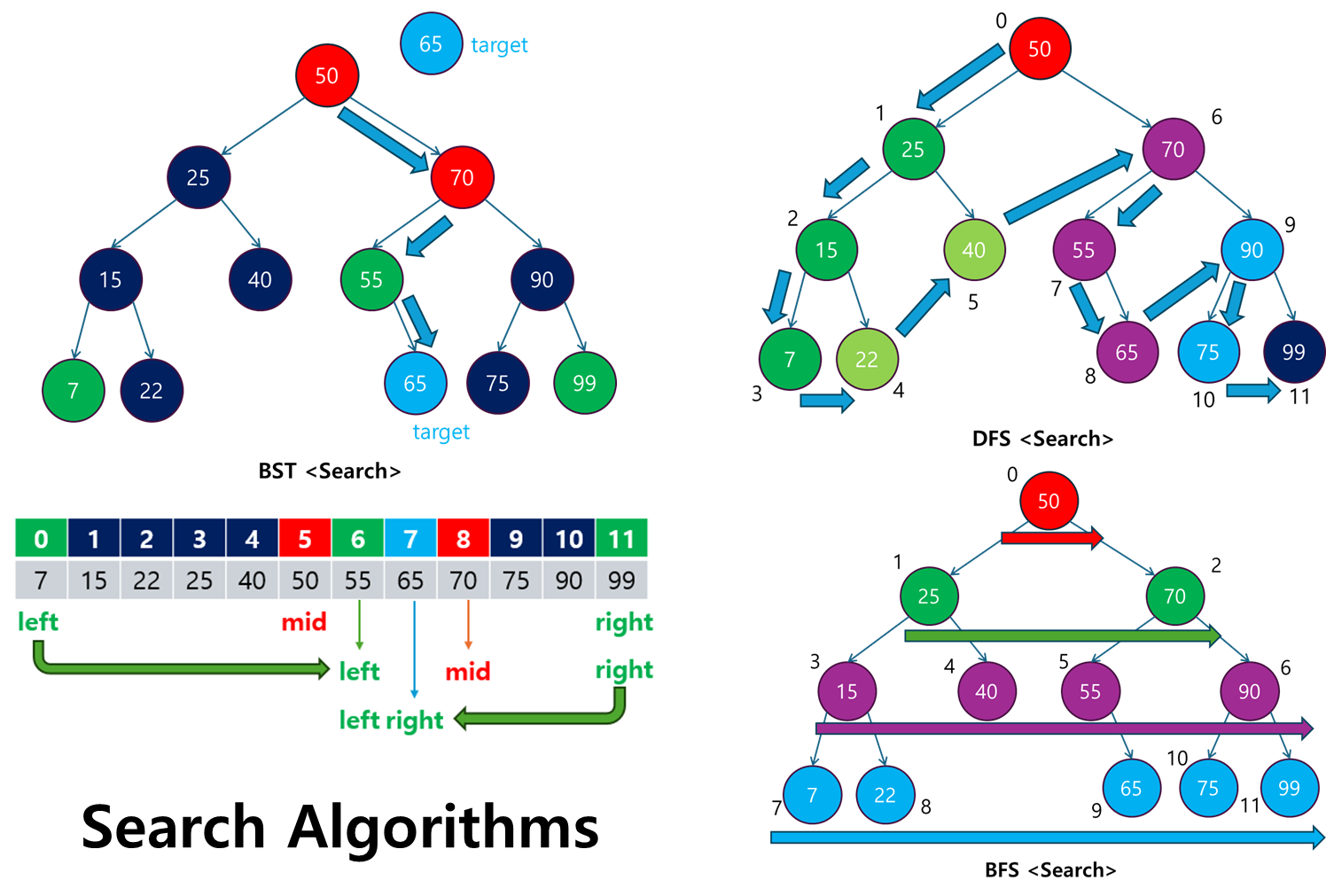
1. 탐색(Search) 알고리즘이란?

탐색(Search) 알고리즘은 주어진 데이터 구조 내에서 원하는 데이터를 찾아내기 위한 일련의 과정입니다.

  • 배열, 트리, 그래프와 같은 자료구조에서 특정 값을 찾거나, 문제에서 요구하는 조건에 맞는 해답을 도출할 때 사용됩니다.
  • 효율적인 탐색 알고리즘을 활용하면 시간과 자원을 절약할 수 있으며, 특히 데이터의 규모가 커질수록 그 중요성이 커집니다.

탐색 알고리즘은 크게 두 가지 범주로 나눌 수 있습니다:

  1. 배열 기반 탐색
    배열을 기반으로 원하는 값을 찾거나 조건을 만족하는 요소를 탐색하는 알고리즘입니다.
  • 선형 탐색(Linear Search): 배열을 처음부터 끝까지 하나씩 살펴보며 찾는 방식. 가장 기본적인 탐색 방법이지만, 속도가 느립니다.
  • 이진 탐색(Binary Search): 정렬된 배열에서 중간 값을 기준으로 탐색 범위를 절반으로 좁혀가며 찾는 방식. 시간 복잡도가 O(log n)으로 매우 효율적입니다.
  • 투 포인터(Two-Pointer): 배열의 양쪽 끝에서 시작해 조건을 만족할 때까지 포인터를 조정하는 방식. 주로 정렬된 배열에서 두 수의 합 등을 찾는 문제에 사용됩니다.
  1. 그래프 및 트리 기반 탐색
    트리나 그래프와 같은 비선형 자료구조에서 특정 값을 찾는 알고리즘입니다.
  • 깊이 우선 탐색(DFS): 한 경로를 끝까지 탐색한 후, 다른 경로로 백트래킹하며 탐색하는 방식. 순환 구조나 경로 찾기 문제에 유용합니다.
  • 너비 우선 탐색(BFS): 시작 지점에서 가까운 노드를 먼저 탐색하며 점진적으로 넓혀가는 방식. 최단 경로 탐색 문제에 적합합니다.
  • 백트래킹(Backtracking): 가능한 모든 경로를 탐색하되, 유망하지 않은 경로는 중간에 포기하는 방식. 그래프나 트리뿐만 아니라 배열에서 순열, 조합, 부분집합을 찾는 문제에도 자주 사용됩니다.

이번 시리즈에서는 이러한 다양한 탐색 알고리즘을 순차적으로 다루면서 그 개념과 활용 방법을 소개합니다.

저번 포스팅에서 배열 기반의 투 포인터(Two-Pointer)와 이진 탐색(Binary Search)을 중점적으로 다루었고, 이번 포스팅에서는 깊이 우선 탐색(DFS), 너비 우선 탐색(BFS)을 중점적으로 다루도록 하겠습니다.

2. DFS(Depth-First Search, 깊이 우선 탐색)

깊이 우선 탐색(DFS)은 트리나 그래프와 같은 자료구조에서 한 경로를 끝까지 탐색한 후, 다른 경로로 백트래킹(backtracking)하며 탐색을 진행하는 알고리즘입니다.

  • DFS는 재귀와 스택을 사용해 탐색을 수행하며, 주로 순환 구조나 경로 찾기 문제에서 매우 유용하게 사용됩니다.
  • DFS는 탐색 깊이를 우선시하며, 트리나 그래프에서 모든 경로를 확인하고자 할 때 유리합니다.

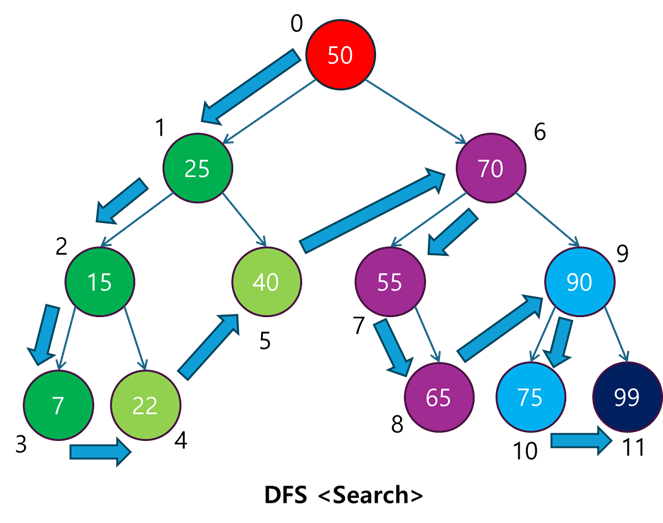
2.1 DFS 알고리즘의 동작 원리

DFS는 한 경로를 끝까지 탐색한 후에 다음 경로로 이동하는 방식으로, 탐색 깊이가 우선시됩니다. 다음은 DFS의 주요 단계입니다:

  1. 시작 노드를 방문하고, 해당 노드를 방문 처리합니다.
  2. 방문하지 않은 인접 노드를 방문합니다. 모든 인접 노드를 순차적으로 방문하면서, 방문하지 않은 노드를 발견할 때마다 그 노드를 탐색합니다.
  3. 탐색을 계속 진행하다가 더 이상 방문할 노드가 없을 경우, 백트래킹하여 이전 노드로 돌아갑니다.
  4. 다시 인접한 노드 중 방문하지 않은 노드가 있다면, 그 노드로 이동하여 탐색을 반복합니다.
  5. 모든 노드가 방문될 때까지 이 과정을 반복합니다.

DFS는 재귀 호출뿐만 아니라 스택 자료구조를 통해 반복문 방식으로도 구현할 수 있습니다.

  • 스택을 사용한 DFS는 명시적으로 스택을 사용해 순차적으로 노드를 방문하며, 재귀 호출 방식과 탐색 순서의 차이가 발생할 순 있지만, 기본적인 원리는 동일합니다.

2.2 DFS 알고리즘 예시 (재귀 호출 방식)

다음 그래프에서 DFS를 사용하여 노드 1에서 탐색을 시작하는 과정을 살펴보겠습니다.

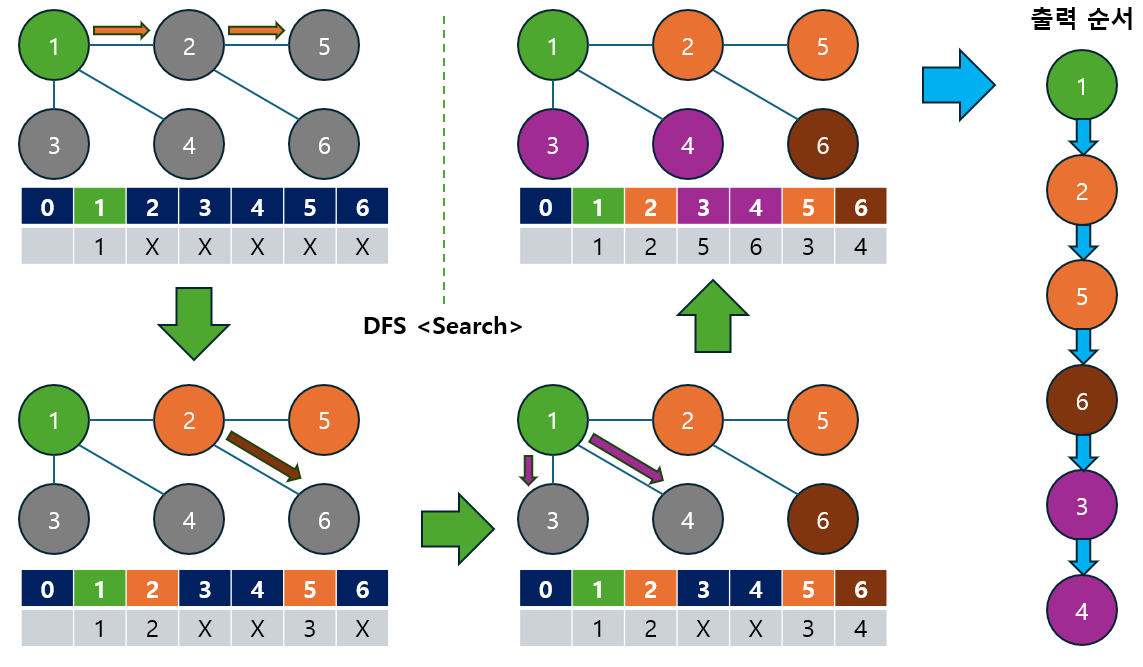
DFS 탐색 순서 : 1 -> 2 -> 5 -> 6 -> 3 -> 4

  • DFS는 경로를 깊게 따라 내려가며, 가능한 한 끝까지 탐색한 후, 다시 돌아와 새로운 경로를 찾습니다.

DFS를 재귀적으로 구현한 코드 (Python):

def dfs(graph, node, visited):
    # 현재 노드를 방문 처리
    visited[node] = True
    print(node, end=' ')
    
    # 현재 노드와 연결된 다른 노드를 재귀적으로 방문
    for neighbor in graph[node]:
        if not visited[neighbor]:
            dfs(graph, neighbor, visited)

# 그래프를 인접 리스트로 표현 (0번 노드는 사용하지 않음)
graph = {
    1: [2, 3, 4],
    2: [1, 5, 6],
    3: [1],
    4: [1],
    5: [2],
    6: [2]
}

# 방문한 노드를 기록할 리스트
visited = [False] * 7

# DFS 시작 (노드 1부터 탐색 시작)
dfs(graph, 1, visited)	# 1 2 5 6 3 4

DFS를 재귀적으로 구현한 코드 (Java):

import java.util.*;

public class DFSExample {
    public static void dfs(int node, boolean[] visited, Map<Integer, List<Integer>> graph) {
        // 현재 노드를 방문 처리
        visited[node] = true;
        System.out.print(node + " ");
        
        // 현재 노드와 연결된 다른 노드를 재귀적으로 방문
        for (int neighbor : graph.get(node)) {
            if (!visited[neighbor]) {
                dfs(neighbor, visited, graph);
            }
        }
    }

    public static void main(String[] args) {
        // 그래프를 인접 리스트로 표현 (1-based index)
        Map<Integer, List<Integer>> graph = new HashMap<>();
        graph.put(1, Arrays.asList(2, 3, 4));
        graph.put(2, Arrays.asList(1, 5, 6));
        graph.put(3, Arrays.asList(1));
        graph.put(4, Arrays.asList(1));
        graph.put(5, Arrays.asList(2));
        graph.put(6, Arrays.asList(2));
        
        // 방문한 노드를 기록할 배열
        boolean[] visited = new boolean[7];
        
        // DFS 시작 (노드 1부터 탐색 시작)
        dfs(1, visited, graph);	// 1 2 5 6 3 4 
    }
}

2.3 DFS 알고리즘 예시 (명시적 스택 방식)

DFS는 재귀 호출을 통해 쉽게 구현할 수 있지만, 명시적인 스택 자료구조를 사용하여 반복문 방식으로도 구현할 수 있습니다.

  • 재귀 호출은 내부적으로 스택을 사용하기 때문에, 명시적 스택을 사용하는 방식은 재귀 호출과 본질적으로 동일하지만, 스택 오버플로우를 방지할 수 있는 장점이 있습니다.

예시 설명:
다음 그래프에서 DFS를 스택 자료구조를 사용하여 노드 1에서 탐색을 시작하는 과정을 살펴보겠습니다.

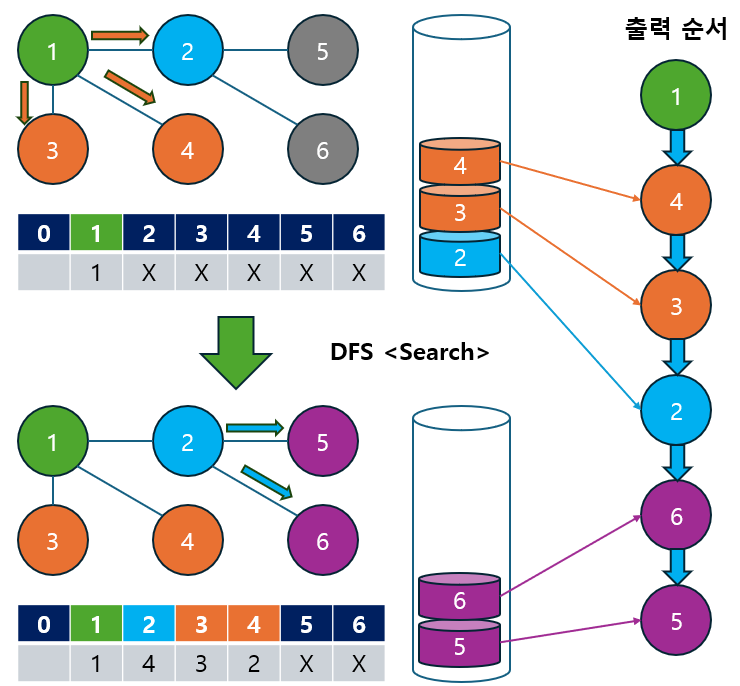
DFS 탐색 순서 : 1 -> 4 -> 3 -> 2 -> 6 -> 5

  • 재귀 호출 방식과 동일한 원리로 작동하지만, 스택의 후입선출(LIFO) 특성 때문에, 인접 노드가 스택에 추가되는 순서에 따라 탐색 순서가 달라질 수 있습니다.
    • 즉, 인접 노드를 어떤 순서로 스택에 넣느냐에 따라 경로가 달라집니다.
    • 예를 들어, 위 코드에서 역순으로 인접 노드를 추가하면 재귀 호출 방식과 동일한 탐색 순서를 유지할 수 있습니다.

DFS를 명시적 스택으로 구현한 코드 (Python):

def dfs_stack(graph, start):
    visited = [False] * (max(graph.keys()) + 1)  # 최대 노드 번호에 맞게 visited 리스트 크기 설정
    stack = [start]  # 시작 노드를 스택에 넣음

    while stack:
        node = stack.pop()
        if not visited[node]:
            print(node, end=' ')
            visited[node] = True
            # 스택에 인접 노드를 추가
            # 스택의 특성상 후입선출(LIFO)이기 때문에, 
            # 인접 노드가 추가되는 순서에 따라 탐색 순서가 달라질 수 있습니다.
            stack.extend(graph[node])

# 테스트용 그래프
graph = {
    1: [2, 3, 4],
    2: [1, 5, 6],
    3: [1],
    4: [1],
    5: [2],
    6: [2]
}

print()
# DFS 시작 (노드 1부터 탐색 시작)
dfs_stack(graph, 1)  # 출력: 1 4 3 2 6 5

DFS를 명시적 스택으로 구현한 코드 (Java):

import java.util.*;

public class DFSStackExample {
    public static void dfsStack(int start, Map<Integer, List<Integer>> graph) {
        boolean[] visited = new boolean[graph.size() + 1];  // 방문한 노드를 기록할 배열
        Stack<Integer> stack = new Stack<>();
        stack.push(start);  // 시작 노드를 스택에 넣음

        while (!stack.isEmpty()) {
            int node = stack.pop();
            if (!visited[node]) {
                System.out.print(node + " ");
                visited[node] = true;

                // 스택에 인접 노드를 추가
                // 후입선출(LIFO) 방식이므로, 인접 노드를 역순으로 추가하여 재귀 호출과 동일한 순서를 유지할 수 있습니다.
                List<Integer> neighbors = graph.get(node);
                Collections.reverse(neighbors);  // 역순으로 추가
                for (int neighbor : neighbors) {
                    if (!visited[neighbor]) {
                        stack.push(neighbor);
                    }
                }
            }
        }
    }

    public static void main(String[] args) {
        // 그래프를 인접 리스트로 표현 (1-based index)
        Map<Integer, List<Integer>> graph = new HashMap<>();
        graph.put(1, Arrays.asList(2, 3, 4));
        graph.put(2, Arrays.asList(1, 5, 6));
        graph.put(3, Arrays.asList(1));
        graph.put(4, Arrays.asList(1));
        graph.put(5, Arrays.asList(2));
        graph.put(6, Arrays.asList(2));

        // DFS 시작 (노드 1부터 탐색 시작)
        dfsStack(1, graph);  // 출력: 1 2 5 6 3 4
    }
}

2.4 DFS 순서 차이의 예시:

재귀 호출 방식과 스택 방식에서의 탐색 순서가 어떻게 달라질 수 있는지 예시로 설명하면 다음과 같습니다:

  1. 재귀 호출 방식:

    • 탐색 순서: 1 → 2 → 5 → 6 → 3 → 4
    • 한 경로를 끝까지 따라가고, 더 이상 갈 곳이 없으면 이전 경로로 백트래킹합니다.

  2. 스택 방식 (기본 순서로 인접 노드 추가):

    • 탐색 순서: 1 → 4 → 3 → 2 → 6 → 5
    • 후입선출(LIFO) 특성에 따라, 가장 최근에 추가된 노드가 먼저 처리되므로, 경로가 달라질 수 있습니다.

  3. 스택 방식 (인접 노드를 역순으로 추가):

    • 탐색 순서: 1 → 2 → 5 → 6 → 3 → 4
    • 재귀 호출 방식과 동일한 순서를 유지하기 위해 인접 노드를 역순으로 스택에 넣어 처리합니다.

2.5 DFS의 시간 복잡도

DFS의 시간 복잡도는 O(V + E)입니다. 여기서:

  • V는 그래프의 노드 수 (정점 수)
  • E는 그래프의 간선 수를 나타냅니다.

DFS는 모든 노드를 방문하고, 각 노드에서 연결된 모든 간선을 확인하므로 V + E에 비례하는 시간이 소요됩니다.

2.6 DFS의 장점과 한계

장점:

  • 메모리 효율성:
    • DFS는 트리나 그래프의 깊이를 우선으로 탐색하기 때문에, 메모리 사용량이 비교적 적습니다.
    • 특히, 재귀 방식으로 구현할 때는 스택 오버플로우에 주의해야 하지만, 일반적으로 메모리 사용량이 BFS보다 적을 수 있습니다.
  • 경로 탐색에 유리:
    • DFS는 경로 탐색이나 사이클 탐지와 같은 문제에서 매우 유용합니다.
    • 예를 들어, 미로 탐색과 같은 문제에서 한 경로를 끝까지 따라가는 방식은 효과적입니다.

한계:

  • 최단 경로 탐색에 적합하지 않음:
    • DFS는 깊이 우선 탐색이기 때문에 최단 경로를 보장하지 않습니다. 최단 경로 탐색 문제에서는 BFS가 더 적합합니다.
  • 깊이 제한 문제:
    • 그래프의 깊이가 너무 깊으면, 재귀 호출로 인해 스택 오버플로우가 발생할 수 있습니다. 이 경우, 반복문을 사용한 스택 기반 DFS가 더 안전합니다.

3. BFS(Breadth-First Search, 너비 우선 탐색)

너비 우선 탐색(BFS)은 트리나 그래프에서 가까운 노드부터 차례대로 탐색하는 알고리즘입니다.

  • BFS는 큐(Queue) 자료구조를 사용하여 가장 가까운 노드부터 넓게 탐색하는 방식을 채택합니다.
  • 최단 경로 탐색 문제에서 많이 사용되며, 모든 경로가 동일한 가중치일 때 최단 경로를 찾는 데 매우 유용합니다.

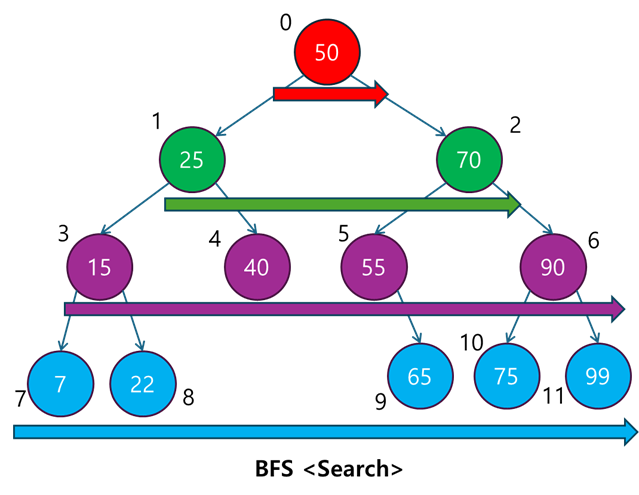
BFS의 주요 특징:

  • 넓이 우선 탐색: DFS는 한 경로를 끝까지 탐색하지만, BFS는 인접한 노드들부터 차례대로 탐색합니다.
  • 최단 경로 보장: 모든 간선의 가중치가 동일하다면, BFS는 최단 경로를 보장합니다.
  • 큐(Queue)를 사용: 탐색 과정에서 큐(Queue) 자료구조를 사용하여, 먼저 큐에 들어간 노드를 먼저 탐색하는 선입선출(FIFO) 구조를 따릅니다.

3.1 BFS 알고리즘의 동작 원리

BFS는 큐를 사용하여 노드를 탐색합니다. 다음은 BFS의 주요 단계입니다:

  1. 시작 노드를 방문하고, 해당 노드를 방문 처리한 후 큐에 넣습니다.
  2. 큐에서 노드를 하나씩 꺼내 그 노드에 연결된 방문하지 않은 인접 노드들을 모두 큐에 추가합니다.
  3. 방문하지 않은 인접 노드들을 방문 처리한 후, 이들을 큐에 넣습니다.
  4. 이 과정을 큐가 빌 때까지 반복합니다.
    • 큐에 들어간 노드들이 탐색되면서, 탐색 범위가 넓어집니다.

3.2 BFS 알고리즘 예시

다음 그래프에서 BFS를 사용하여 노드 1에서 탐색을 시작하는 과정을 살펴보겠습니다.

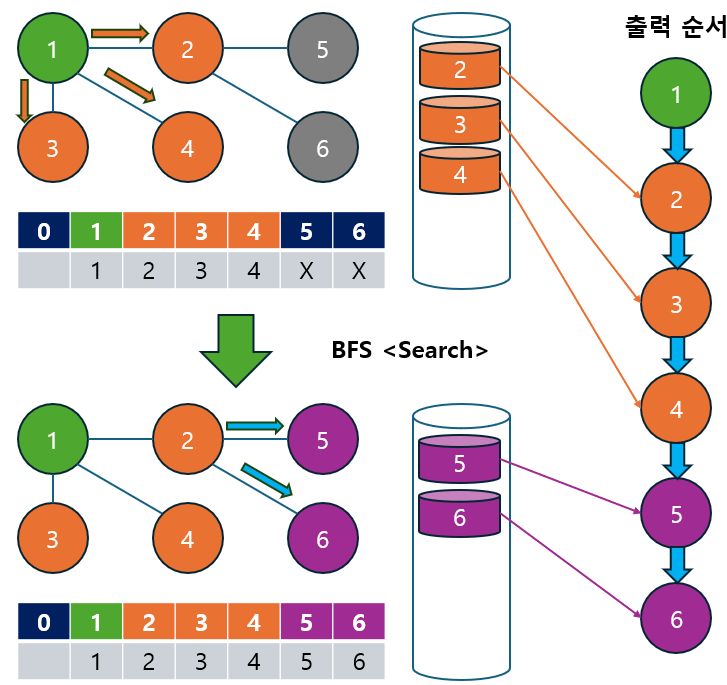
BFS 탐색 순서 : 1 -> 2 -> 3 -> 4 -> 5 -> 6

  • BFS는 시작 노드에서 가까운 순서대로 탐색하기 때문에, 각 노드를 넓이 우선으로 차례대로 방문하게 됩니다.

BFS를 구현한 코드 (Python):

from collections import deque

def bfs(graph, start):
    visited = [False] * (max(graph.keys()) + 1)  # 최대 노드 번호에 맞게 visited 리스트 크기 설정
    queue = deque([start])  # 큐에 시작 노드를 넣음
    visited[start] = True   # 시작 노드를 방문 처리

    while queue:
        node = queue.popleft()  # 큐에서 노드를 꺼냄
        print(node, end=' ')

        # 현재 노드와 연결된, 아직 방문하지 않은 모든 노드를 큐에 추가
        for neighbor in graph[node]:
            if not visited[neighbor]:
                queue.append(neighbor)
                visited[neighbor] = True  # 방문 처리

# 테스트용 그래프
graph = {
    1: [2, 3, 4],
    2: [1, 5, 6],
    3: [1],
    4: [1],
    5: [2],
    6: [2]
}

print()
# BFS 시작 (노드 1부터 탐색 시작)
bfs(graph, 1)  # 출력: 1 2 3 4 5 6

BFS를 구현한 코드 (Java):

import java.util.*;

public class BFSExample {
    public static void bfs(int start, Map<Integer, List<Integer>> graph) {
        boolean[] visited = new boolean[graph.size() + 1];  // 방문한 노드를 기록할 배열
        Queue<Integer> queue = new LinkedList<>();
        queue.offer(start);  // 큐에 시작 노드를 넣음
        visited[start] = true;  // 시작 노드를 방문 처리

        while (!queue.isEmpty()) {
            int node = queue.poll();  // 큐에서 노드를 꺼냄
            System.out.print(node + " ");

            // 현재 노드와 연결된, 아직 방문하지 않은 모든 노드를 큐에 추가
            for (int neighbor : graph.get(node)) {
                if (!visited[neighbor]) {
                    queue.offer(neighbor);
                    visited[neighbor] = true;  // 방문 처리
                }
            }
        }
    }

    public static void main(String[] args) {
        // 그래프를 인접 리스트로 표현 (1-based index)
        Map<Integer, List<Integer>> graph = new HashMap<>();
        graph.put(1, Arrays.asList(2, 3, 4));
        graph.put(2, Arrays.asList(1, 5, 6));
        graph.put(3, Arrays.asList(1));
        graph.put(4, Arrays.asList(1));
        graph.put(5, Arrays.asList(2));
        graph.put(6, Arrays.asList(2));

        // BFS 시작 (노드 1부터 탐색 시작)
        bfs(1, graph);  // 출력: 1 2 3 4 5 6
    }
}

3.3 BFS의 시간 복잡도

BFS의 시간 복잡도는 O(V + E)입니다. 여기서:

  • V는 그래프의 노드 수 (정점 수)
  • E는 그래프의 간선 수를 나타냅니다.

BFS는 모든 노드를 방문하고, 각 노드에서 연결된 모든 간선을 확인하므로 V + E에 비례하는 시간이 소요됩니다. 이는 DFS의 시간 복잡도와 동일합니다.

3.4 BFS의 장점과 한계

장점:

  • 최단 경로 탐색에 유리: BFS는 간선의 가중치가 동일한 그래프에서 최단 경로를 보장하는 알고리즘입니다. 이를 통해 미로 탐색이나 네트워크 탐색에서 최단 경로를 쉽게 찾을 수 있습니다.
  • 순차적인 탐색: 인접한 노드를 먼저 방문하므로, 특정 노드와 가장 가까운 노드를 먼저 탐색할 수 있습니다.

한계:

  • 메모리 사용량: BFS는 노드를 방문할 때마다 큐에 인접한 노드들을 모두 저장하기 때문에, 노드 수가 많거나 그래프가 매우 넓으면 메모리 사용량이 많아질 수 있습니다.
  • 깊은 그래프에서 비효율적: 깊이가 매우 깊은 그래프의 경우, 큐에 저장해야 할 노드가 많아지므로 메모리와 성능 측면에서 비효율적일 수 있습니다.

4. DFS와 BFS 비교

DFS와 BFS는 모두 그래프나 트리 구조에서 자주 사용하는 탐색 알고리즘이지만, 탐색 방식과 응용 분야에서 차이가 있습니다.
이 파트에서는 두 알고리즘을 비교하여 그 차이점과 사용 시 유리한 상황을 살펴보겠습니다.

4.1 탐색 방식 비교

알고리즘탐색 방식사용 자료구조탐색 순서최단 경로 보장
DFS깊이 우선 탐색스택
(또는 재귀 호출)		한 경로를 끝까지 탐색최단 경로를 보장하지 않음
BFS너비 우선 탐색큐 (FIFO)가까운 노드부터 차례로 탐색최단 경로를 보장
(가중치가 동일할 경우)

  • DFS는 탐색 깊이를 우선시하며, 한 경로를 끝까지 탐색한 후 다른 경로를 탐색하는 방식입니다.

    • 스택이나 재귀 호출을 사용해 후입선출(LIFO) 구조로 탐색하며, 깊이 우선으로 진행하기 때문에 특정 경로의 끝까지 탐색 후 다른 경로로 이동합니다.

  • BFS는 탐색 범위를 넓게하며, 시작점에서 가까운 노드부터 차례대로 탐색하는 방식입니다.

    • 큐를 사용해 선입선출(FIFO) 구조로 탐색하며, 넓이 우선으로 탐색하면서 최단 경로를 보장합니다.

4.2 시간 복잡도 비교

DFS와 BFS 모두 시간 복잡도는 O(V + E)로 동일합니다.

  • V는 그래프의 노드 수(정점 수)
  • E는 그래프의 간선 수를 의미합니다.

각 노드를 방문하고, 각 노드에 연결된 모든 간선을 확인하는 데 걸리는 시간이 탐색 시간에 영향을 미칩니다.

4.3 메모리 사용 비교

알고리즘메모리 사용특성
DFS비교적 적음
(재귀 깊이에 비례)		트리나 그래프가 매우 깊을 경우
스택 오버플로우가 발생할 수 있음
BFS비교적 큼
(큐 크기에 비례)		트리나 그래프가 매우 넓을 경우
큐가 커져 메모리 사용량 증가
  • DFS는 메모리 사용량이 적은 편이지만, 그래프나 트리의 깊이가 너무 깊어지면 스택 오버플로우 문제가 발생할 수 있습니다.
  • BFS는 탐색 과정에서 모든 인접 노드를 큐에 저장하기 때문에, 탐색 범위가 넓을수록 메모리 사용량이 증가합니다.

4.4 주요 응용 분야

알고리즘주요 응용 분야
DFS경로 탐색 (미로 찾기, 사이클 탐지)
위상 정렬
강한 연결 요소
BFS최단 경로 탐색 (미로 탐색, 네트워크 경로 탐색)
최소 신장 트리 (가중치가 동일할 때)
그래프 레벨 탐색
  • DFS는 주로 경로를 찾거나 사이클을 탐지하는 문제에 유리합니다. 또한 위상 정렬이나 강한 연결 요소를 찾는 문제에서도 DFS가 자주 사용됩니다.
  • BFS는 최단 경로를 보장하는 특성 때문에 미로 탐색이나 네트워크 경로 탐색에서 많이 사용됩니다. 특히 간선의 가중치가 동일한 경우, 최단 경로 문제를 해결할 때 BFS가 유용합니다.

4.5 사용 시 유리한 상황

  • DFS가 유리한 상황:

    • 경로의 깊이를 우선적으로 탐색해야 할 때
    • 사이클을 찾거나 트리나 그래프에서 특정 경로를 찾는 문제에 적합
    • 재귀 호출을 사용하여 간단히 구현할 수 있는 경우
    • 메모리 사용량을 최소화해야 하는 상황에서 적합

  • BFS가 유리한 상황:

    • 최단 경로를 보장해야 하는 상황
    • 노드 간의 최단 거리를 찾아야 하는 문제에서 유리
    • 큐 자료구조를 사용한 탐색이 적합한 경우
    • 그래프가 너비가 넓고 깊이가 얕은 경우

마무리

이번 포스팅에서는 DFS(깊이 우선 탐색)과 BFS(너비 우선 탐색)의 개념과 그 차이점을 살펴보았습니다.

  • DFS는 깊이 우선으로 경로를 탐색하여 경로 탐색이나 사이클 탐지와 같은 문제에 유용합니다.
  • BFS는 너비 우선으로 탐색하여 최단 경로 탐색 문제에 매우 적합합니다.

다음 포스팅에서는 백트래킹(Backtracking)에 대해 다루며, 어떻게 탐색 과정에서 불필요한 경로를 제거하고 효율적으로 문제를 해결할 수 있는지 설명할 예정입니다.

profile
Kyung Jae, Cheong
일 때문에 포스팅은 잠시 쉬어요 ㅠ 바쁘다 바빠 모두들 화이팅! // Machine Learning (AI) Engineer & BackEnd Engineer (Entry)
이전 포스트

[알고리즘] 탐색(Search) - Two-Pointer & Binary Search [개념과 활용]

다음 포스트

[알고리즘] 탐색(Search) & 최적화(Optimizing) - BackTracking (백트래킹)

0개의 댓글