[알고리즘] 최적화(Optimizing) - Dynamic (동적) Programming [개념과 활용]

Kyung Jae, Cheong·2024년 10월 25일

Java python 알고리즘

알고리즘-Algorithms

목록 보기

13/15

본 시리즈는 프로그래밍 알고리즘의 개념을 정리하고 실습을 진행해보는 시리즈입니다.

실습은 다음과 같은 개발환경 및 버전에서 진행하였습니다.
- IDE : IntelliJ IDEA (Ultimate Edition)
- Java : JDK 21 (corretto-21)
- Python : 3.9 (conda env)

최적화(Optimizing) - Greedy

1. 최적화(Optimizing) 알고리즘이란?

최적화 알고리즘은 주어진 문제에서 가장 효율적인 해를 찾는 알고리즘입니다.

이러한 알고리즘들은 여러 가능한 해들 중에서 최적의 해를 선택하는 과정을 거칩니다.
최적화 문제는 여러 분야에서 사용되며, 다양한 문제에 대해 다른 방식으로 최적화를 접근할 수 있습니다.

대표적으로 백트래킹, 그리디, 동적 프로그래밍(DP) 이 세 가지 방법이 많이 사용되며, 각각의 방식은 문제에 대한 접근법과 해를 찾는 과정이 다릅니다.

백트래킹: 가능한 모든 해를 탐색하되, 유망하지 않은 경로는 배제함으로써 탐색 범위를 축소하는 방식.
그리디(Greedy): 매 순간 가장 최적이라고 판단되는 선택을 하고 그 선택을 기반으로 문제를 해결하는 방식.
동적 프로그래밍(DP): 문제를 작은 부분 문제로 나누고 그 결과를 저장하여 중복 계산을 피하며 최적해를 찾는 방식.

최적화 알고리즘의 주요 특징

탐색 공간 축소
최적화 알고리즘은 모든 경우의 수를 탐색하지 않고, 효율적으로 해를 찾기 위해 탐색 공간을 축소합니다.
- 백트래킹: 비효율적인 경로를 조기에 배제해 탐색 공간을 줄입니다.
- 그리디: 매번 가장 작은 비용이나 최대 이익을 선택해 빠르게 해를 찾습니다.
- 동적 프로그래밍: 부분 문제의 결과를 저장하여 중복된 계산을 줄임으로써 성능을 최적화합니다.
해의 최적성 보장 여부
최적화 알고리즘은 해의 최적성 보장 여부가 다릅니다.
- 백트래킹과 동적 프로그래밍: 가능한 모든 경로를 탐색하거나, 문제를 나누어 최적해를 보장합니다.
- 그리디: 매 순간 최선의 선택을 하지만, 그 선택이 전체적으로 최적해를 보장하지는 않습니다.
문제 유형에 맞는 최적화 방식
각 최적화 기법은 문제 유형에 따라 적합한 방식이 다릅니다.
- 백트래킹: 모든 해를 탐색해야 할 때 적합하며, 주로 조합 탐색이나 경로 탐색 문제에 자주 사용됩니다.
- 그리디: 각 단계에서 내리는 선택이 최종적으로도 최적해로 이어질 때 효과적입니다.
  - 예를 들어, 최소 신장 트리, 최단 경로 문제에서 많이 사용됩니다.
- 동적 프로그래밍: 문제를 작은 문제로 분할하고 이전 결과를 재사용할 수 있는 구조일 때 매우 효율적입니다.
  - 대표적으로 최적 부분 구조를 가진 문제에 자주 적용됩니다.

이번 포스팅에서는 대표적인 최적화 방식 중에서 동적 프로그래밍(Dynamic Programming, DP)에 대해서 다루어 보고자 합니다.

2. Dynamic Programming이란?

동적 프로그래밍(Dynamic Programming, DP)은 최적 부분 구조(Optimal Substructure)와 중복되는 부분 문제(Overlapping Subproblems)를 가진 문제를 효율적으로 해결하는 방법론입니다.

이는 문제를 여러 개의 작은 부분 문제로 나누고, 각 부분 문제를 한 번만 계산한 후 그 결과를 저장함으로써 전체 문제의 해결에 활용하는 방식입니다.

2.1 DP의 핵심 개념:

최적 부분 구조 (Optimal Substructure):
- 큰 문제의 최적해가 작은 부분 문제들의 최적해로 구성될 수 있을 때 최적 부분 구조를 가진다고 합니다.
- 예를 들어, 피보나치 수열에서는 F(n) = F(n-1) + F(n-2)라는 최적 부분 구조 관계가 성립합니다.
- 이처럼 큰 문제의 해를 작은 문제들의 해로 쉽게 나눌 수 있는 경우, DP가 유용하게 적용됩니다.
중복되는 부분 문제 (Overlapping Subproblems):
- 동일한 부분 문제가 여러 번 반복해서 계산되는 경우, 중복된 계산을 피하기 위해 계산된 결과를 저장하여 다시 사용하는 방식입니다.
- 예를 들어, 피보나치 수열을 재귀적으로 계산할 때 F(2)나 F(3) 등이 여러 번 호출되는데, DP는 이 중복 계산을 제거함으로써 효율성을 극대화합니다.

2.2 DP와 분할 정복의 차이점:

분할 정복(Divide and Conquer)도 문제를 작은 부분 문제로 나누는 방식이지만, DP와는 중요한 차이가 있습니다.

분할 정복은 부분 문제들이 서로 독립적이기 때문에 각 문제를 해결할 때 이미 계산된 값을 재사용하지 않습니다.
DP는 중복되는 부분 문제가 발생할 때, 이미 계산된 값을 저장하여 이를 재사용하는 데 중점을 둡니다.

예를 들어, 퀵소트(Quick Sort)와 같은 분할 정복 기법에서는 각 부분 문제가 독립적이라 값을 따로 저장하거나 재사용할 필요가 없지만, DP에서는 중복 계산을 피하기 위해 결과를 저장하고 재사용하는 방식이 핵심입니다.

2.3 DP의 두 가지 방식:

Memoization(메모이제이션):
- 탑다운(Top-down) 방식으로, 재귀적으로 문제를 해결하며 중복되는 계산을 피하기 위해 결과를 저장하는 방식입니다.
Tabulation(테이블링):
- 바텀업(Bottom-up) 방식으로, 작은 문제부터 차례대로 해결해 나가면서 결과를 테이블에 저장하는 방식입니다.

DP는 시간 복잡도를 크게 줄이는 최적화 기법으로, 재귀적 문제 해결에서 발생하는 중복 계산을 방지함으로써 성능을 향상시킵니다.

3. DP 원리 : Tabulation & Memoization

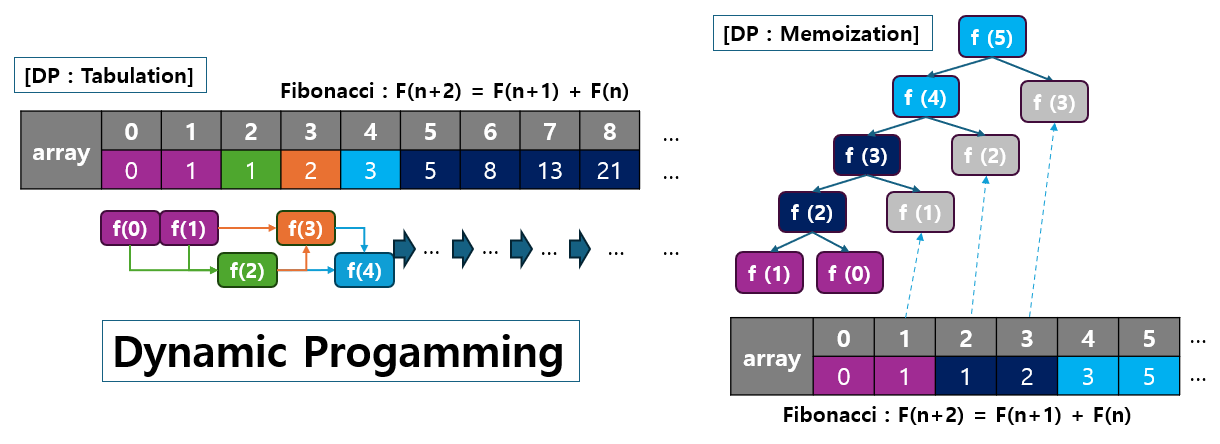
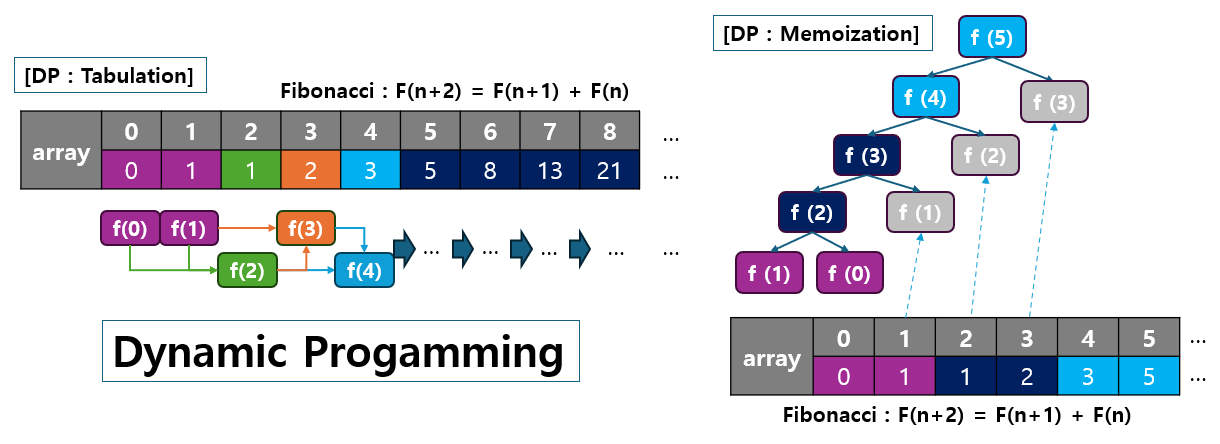
동적 프로그래밍(DP)은 문제를 작은 부분 문제로 나누어 해결하며, 탑다운(Top-down) 방식과 바텀업(Bottom-up) 방식의 두 가지 주요 접근 방법이 있습니다.

이 두 가지 방식은 각각 Memoization(메모이제이션)과 Tabulation(테이블링)이라는 방법으로 구현되며, 각각의 방식이 문제를 해결하는 흐름이 다릅니다.

3.1 Tabulation (테이블링, 바텀업 방식)

Tabulation은 바텀업(Bottom-up) 방식으로, 작은 부분 문제부터 순차적으로 해결하여 큰 문제를 해결하는 방식입니다.

이 방식은 반복문을 사용해 아래에서부터 쌓아 올리듯 문제를 해결하며, 결과를 테이블(배열)에 저장하면서 최종적인 해에 도달합니다.

동작 원리: 작은 부분 문제의 해를 먼저 구한 뒤, 이를 바탕으로 점점 더 큰 문제를 해결합니다.
예시: 피보나치 수열을 바텀업 방식으로 해결할 때, 먼저 F(0)와 F(1)을 구하고, 이를 기반으로 F(2)부터 차례대로 구해 나갑니다.
장단점: 반복문을 사용하므로, 재귀 호출에 따른 스택 오버플로우의 위험이 없고, 메모리 사용량이 효율적일 수 있습니다. 다만, 불필요한 계산이 일부 포함될 수 있습니다.

피보나치 수열 예시 (Tabulation)

def fibonacci_tabulation(n):
    table = [0] * (n + 1)
    table[1] = 1
    
    for i in range(2, n + 1):
        table[i] = table[i - 1] + table[i - 2]
    
    return table[n]

# 예시 실행
print(fibonacci_tabulation(7))  # 출력: 13

3.2 Memoization (메모이제이션, 탑다운 방식)

Memoization은 탑다운(Top-down) 방식으로, 재귀 호출을 사용해 큰 문제를 해결하는 과정에서 작은 부분 문제의 결과를 저장하여 중복 계산을 피하는 방식입니다.

필요한 순간에만 계산을 진행하며, 이미 계산된 부분은 메모이제이션 테이블에 저장된 값을 재사용합니다.

동작 원리: 큰 문제를 재귀적으로 해결하면서, 부분 문제의 결과를 저장하고 중복 계산을 피합니다.
예시: 피보나치 수열을 탑다운 방식으로 해결할 때, F(7)을 구하는 과정에서 F(6), F(5)를 재귀적으로 구하지만, 한 번 계산된 값은 저장하여 이후 재사용합니다.
장단점: 필요한 부분 문제만 계산하기 때문에, 불필요한 계산을 줄일 수 있습니다. 그러나 재귀 호출을 사용할 경우, 스택 오버플로우의 위험이 존재할 수 있습니다.

피보나치 수열 예시 (Memoization)

def fibonacci_memoization(n, memo=None):
    if memo is None:
        memo = [0] * (n + 1)
    
    if n <= 1:
        return n
    if memo[n] != 0:
        return memo[n]
    
    memo[n] = fibonacci_memoization(n - 1, memo) + fibonacci_memoization(n - 2, memo)
    return memo[n]

# 예시 실행
print(fibonacci_memoization(7))  # 출력: 13

3.3 Tabulation vs Memoization

두 가지 방식의 차이점은 계산 순서와 저장 방식에서 나타납니다.

Tabulation: 작은 문제부터 차례대로 계산하여 큰 문제를 해결합니다. 반복문을 사용하며, 결과를 상향식(Bottom-up)으로 구합니다.
Memoization: 큰 문제를 해결하는 과정에서 필요할 때 작은 문제를 재귀적으로 계산합니다. 재귀 함수를 사용하며, 하향식(Top-down)으로 구합니다.

특징	Tabulation (바텀업)	Memoization (탑다운)
계산 방식	작은 문제부터 순차적으로 해결	큰 문제부터 재귀적으로 해결
주요 도구	반복문	재귀 호출
메모리 사용	메모리 사용이 일정	재귀 깊이에 따라 스택 사용
중복 계산	처음부터 계산하여 중복 없음	중복 계산을 피하기 위해 결과 저장

동적 프로그래밍의 두 가지 방식은 문제의 특성에 따라 선택할 수 있으며, 각 방식은 중복 계산을 피하여 성능을 향상시키는 공통 목표를 가집니다.

4. Dynamic Programming 활용 예시

동적 프로그래밍은 다양한 문제에서 효율적으로 활용됩니다.

여기서는 대표적인 예시인 최장 공통 부분 수열(Longest Common Subsequence, LCS)와 배낭 문제(Knapsack Problem)를 Java와 Python으로 구현해 보겠습니다.

4.1 예시 1: 최장 공통 부분 수열 (LCS)

문제 설명:
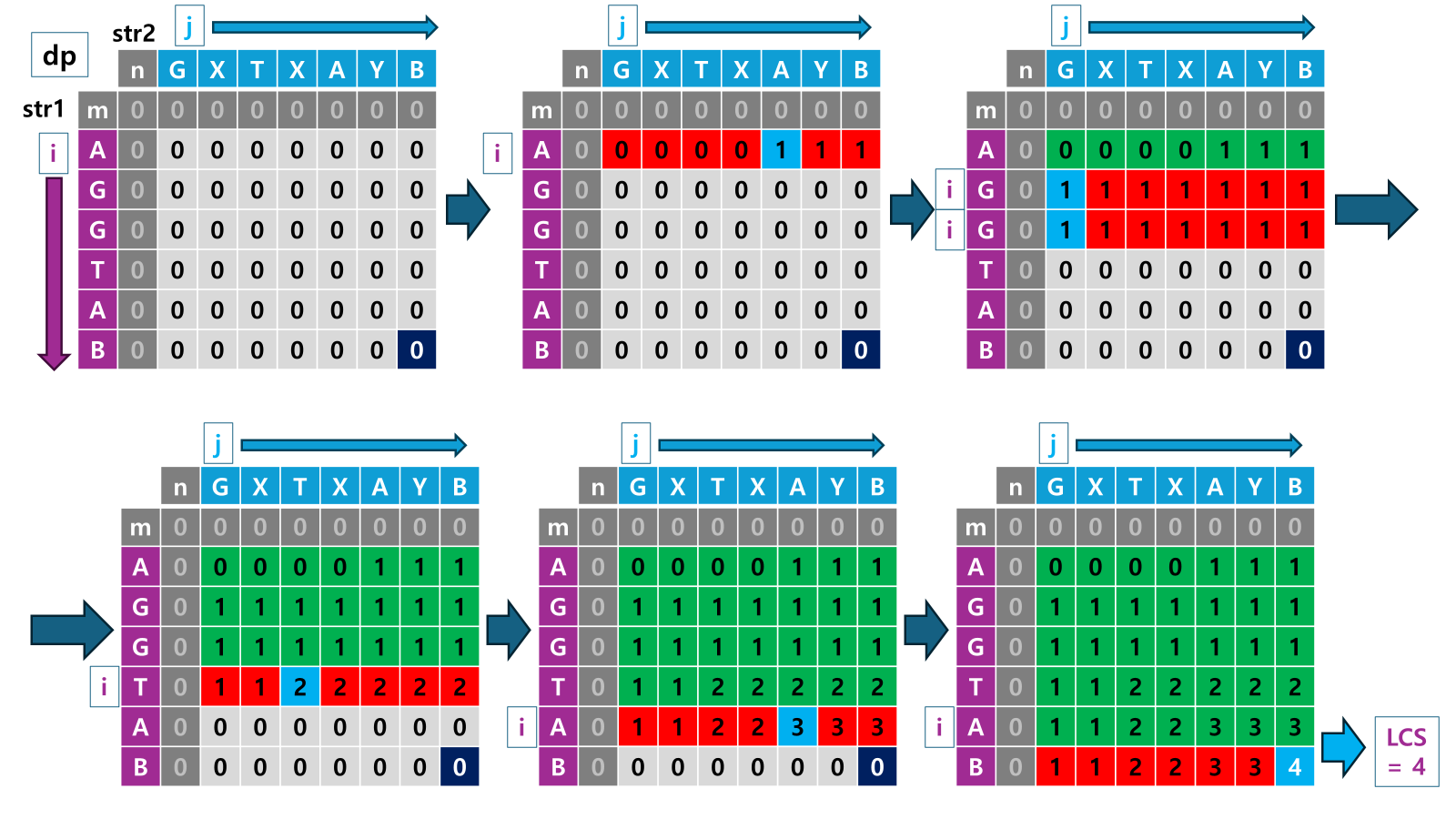
두 개의 문자열이 주어졌을 때, 두 문자열에서 공통적으로 나타나는 부분 수열 중 가장 긴 부분 수열의 길이를 구하는 문제입니다.

Java 구현 (LCS)

public class LCS_DP {
    public static void main(String[] args) {
        String str1 = "AGGTAB";
        String str2 = "GXTXAYB";

        System.out.println("LCS 길이: " + lcs(str1, str2)); // LCS 길이: 4
    }

    public static int lcs(String str1, String str2) {
        int m = str1.length();
        int n = str2.length();
        int[][] dp = new int[m + 1][n + 1];

        for (int i = 0; i <= m; i++) {
            for (int j = 0; j <= n; j++) {
                if (i == 0 || j == 0) {
                    dp[i][j] = 0;
                } else if (str1.charAt(i - 1) == str2.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }
        return dp[m][n];
    }
}

Python 구현 (LCS)

def lcs(str1, str2):
    m, n = len(str1), len(str2)
    dp = [[0] * (n + 1) for _ in range(m + 1)]

    for i in range(1, m + 1):
        for j in range(1, n + 1):
            if str1[i - 1] == str2[j - 1]:
                dp[i][j] = dp[i - 1][j - 1] + 1
            else:
                dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])

    return dp[m][n]


# 예시 실행
str1 = "AGGTAB"
str2 = "GXTXAYB"
print(f"LCS 길이: {lcs(str1, str2)}")  # 출력: LCS 길이: 4

설명:

주어진 두 문자열 str1과 str2에 대해 이중 반복문을 사용해 DP 테이블을 채웁니다.

두 문자가 같을 때는 이전의 값([i-1][j-1])에 1을 더해준 값을 저장합니다.
두 문자가 다를 때는 둘([i-1] or [j-1]) 중 큰 값을 저장합니다.

이 방식으로 공통 부분 수열의 길이를 DP를 통해 효율적으로 구할 수 있습니다.

4.2 예시 2: 배낭 문제 (Knapsack Problem)

문제 설명:
여러 개의 물건이 주어지고, 각 물건은 특정한 무게와 가치를 가집니다.
배낭의 용량을 넘지 않는 선에서 물건을 선택할 때, 물건들의 가치 합이 최대가 되도록 하려면 어떻게 선택해야 할까요?

Java 구현 (Knapsack)

public class Knapsack_DP {
    public static void main(String[] args) {
        int[] weights = {1, 3, 4, 5};
        int[] values = {1, 4, 5, 7};
        int capacity = 7;

        System.out.println("최대 가치: " + knapsack(weights, values, capacity));
        // 출력: 최대 가치: 9
    }

    public static int knapsack(int[] weights, int[] values, int capacity) {
        int n = weights.length;
        int[][] dp = new int[n + 1][capacity + 1];

        for (int i = 1; i <= n; i++) {
            for (int w = 0; w <= capacity; w++) {
                if (weights[i - 1] <= w) {
                    dp[i][w] = Math.max(dp[i - 1][w], dp[i - 1][w - weights[i - 1]] + values[i - 1]);
                } else {
                    dp[i][w] = dp[i - 1][w];
                }
            }
        }
        return dp[n][capacity];
    }
}

Python 구현 (Knapsack)

def knapsack(weights, values, capacity):
    n = len(weights)
    dp = [[0] * (capacity + 1) for _ in range(n + 1)]

    for i in range(1, n + 1):
        for w in range(capacity + 1):
            if weights[i - 1] <= w:
                dp[i][w] = max(dp[i - 1][w], dp[i - 1][w - weights[i - 1]] + values[i - 1])
            else:
                dp[i][w] = dp[i - 1][w]

    return dp[n][capacity]

# 예시 실행
weights = [1, 3, 4, 5]
values = [1, 4, 5, 7]
capacity = 7
print(f"최대 가치: {knapsack(weights, values, capacity)}")
# 출력: 최대 가치: 9

설명:

각 물건에 대해 배낭에 넣을 수 있는 경우와 넣지 않는 경우를 계산하여 DP 테이블을 채웁니다.

무게 제한을 초과하지 않도록 물건을 선택하면서, 물건들의 가치 합을 최대화합니다.

5. Dynamic Programming의 알고리즘 복잡도

동적 프로그래밍(DP)은 시간 복잡도와 공간 복잡도 측면에서 매우 효율적인 알고리즘 기법입니다.

하지만 문제의 구조와 DP 테이블의 크기에 따라 복잡도가 결정되며, 이 복잡도를 정확하게 이해하는 것이 중요합니다.

5.1 시간 복잡도

동적 프로그래밍의 시간 복잡도는 문제를 해결하는 과정에서 필요한 중복 계산을 제거함으로써 크게 줄어듭니다.

예시에서 다룬 DP 문제들의 시간 복잡도는 다음과 같은 방식으로 분석할 수 있습니다.

LCS 문제 (최장 공통 부분 수열)
- 시간 복잡도: O(m * n)
  - m과 n은 각각 두 문자열의 길이입니다.
  - 각 문자의 비교는 이중 반복문을 통해 이루어지며, 테이블의 크기만큼 모든 값을 계산해야 하므로 m * n의 시간이 소요됩니다.
Knapsack 문제 (배낭 문제)
- 시간 복잡도: O(n * W)
  - n은 물건의 개수, W는 배낭의 최대 용량입니다.
  - 각 물건에 대해 배낭 용량의 범위(0부터 W까지)를 모두 계산해야 하므로 n * W의 시간이 소요됩니다.

5.2 공간 복잡도

동적 프로그래밍의 공간 복잡도는 보통 DP 테이블에 의존합니다. 테이블을 사용하는 DP 알고리즘은 각 상태를 저장하여 중복 계산을 피하기 때문에, 테이블의 크기에 따라 공간 복잡도가 결정됩니다.

LCS 문제 (최장 공통 부분 수열)
- 공간 복잡도: O(m * n)
- 두 문자열의 길이에 비례하여 2차원 DP 테이블을 사용하므로, m * n의 공간을 사용합니다.
Knapsack 문제 (배낭 문제)
- 공간 복잡도: O(n * W)
- n개의 물건과 W 크기의 2차원 DP 테이블을 사용하여 물건의 개수와 배낭 용량에 비례하는 공간이 필요합니다.

5.3 공간 복잡도를 줄이는 방법 예시

경우에 따라서는 2차원 테이블을 사용하지 않고 1차원 배열로 공간을 절약할 수 있는 방법도 존재합니다.

예를 들어, 배낭 문제에서 이전 단계의 결과만 필요할 경우, 이전 단계에서 사용된 값을 업데이트하면서 공간을 절약할 수 있습니다.

# 1차원 배열을 이용한 Knapsack 문제 해결 (공간 최적화)
def knapsack_optimized(weights, values, capacity):
    n = len(weights)
    dp = [0] * (capacity + 1)

    for i in range(n):
        for w in range(capacity, weights[i] - 1, -1):
            dp[w] = max(dp[w], dp[w - weights[i]] + values[i])

    return dp[capacity]

# 예시 실행
weights = [1, 3, 4, 5]
values = [1, 4, 5, 7]
capacity = 7
print(f"최대 가치: {knapsack_optimized(weights, values, capacity)}")  
# 출력: 최대 가치: 9

위와 같이 bottom-up 방식으로 1차원 배열을 사용하여 공간 복잡도를 O(n * W)에서 O(W)로 줄일 수 있습니다.

마무리

이번 포스팅에서는 동적 프로그래밍(DP)의 개념과 이를 활용한 대표적인 문제인 최장 공통 부분 수열(LCS)과 배낭 문제(Knapsack Problem)를 살펴보았습니다.

동적 프로그래밍은 최적 부분 구조와 중복되는 부분 문제를 가진 문제를 효율적으로 해결하는 강력한 알고리즘 기법입니다.

핵심 요약:
1. DP의 핵심 원리는 문제를 작은 부분 문제로 나누어 중복 계산을 제거하는 데 있습니다.
2. Memoization은 탑다운 방식, Tabulation은 바텀업 방식으로 각각 문제를 해결합니다.
3. LCS 문제와 Knapsack 문제는 동적 프로그래밍을 사용하는 대표적인 문제로, 효율적인 시간과 공간 복잡도를 통해 최적해를 찾을 수 있습니다.
4. 2차원 DP배열의 1차원 DP배열 변환 등의 공간 최적화를 통해 메모리 사용량을 더 줄일 수도 있습니다.

다음 포스팅부터는 그래프에서 최단 경로를 구하는 알고리즘들에 대해서 다루어 보도록 하겠습니다.

Kyung Jae, Cheong

일 때문에 포스팅은 잠시 쉬어요 ㅠ 바쁘다 바빠 모두들 화이팅! // Machine Learning (AI) Engineer & BackEnd Engineer (Entry)

이전 포스트

[알고리즘] 최적화(Optimizing) - Greedy (탐욕적) 알고리즘 [개념과 활용]

다음 포스트