[알고리즘] 최적화(Optimizing) - Greedy (탐욕적) 알고리즘 [개념과 활용]

Kyung Jae, Cheong·2024년 10월 24일

Java python 알고리즘

알고리즘-Algorithms

목록 보기

12/15

본 시리즈는 프로그래밍 알고리즘의 개념을 정리하고 실습을 진행해보는 시리즈입니다.

실습은 다음과 같은 개발환경 및 버전에서 진행하였습니다.
- IDE : IntelliJ IDEA (Ultimate Edition)
- Java : JDK 21 (corretto-21)
- Python : 3.9 (conda env)

최적화(Optimizing) - Greedy

1. 최적화(Optimizing) 알고리즘이란?

최적화 알고리즘은 주어진 문제에서 가장 효율적인 해를 찾는 알고리즘입니다.

이러한 알고리즘들은 여러 가능한 해들 중에서 최적의 해를 선택하는 과정을 거칩니다.
최적화 문제는 여러 분야에서 사용되며, 다양한 문제에 대해 다른 방식으로 최적화를 접근할 수 있습니다.

대표적으로 백트래킹, 그리디, 동적 프로그래밍(DP) 이 세 가지 방법이 많이 사용되며, 각각의 방식은 문제에 대한 접근법과 해를 찾는 과정이 다릅니다.

백트래킹: 가능한 모든 해를 탐색하되, 유망하지 않은 경로는 배제함으로써 탐색 범위를 축소하는 방식.
그리디(Greedy): 매 순간 가장 최적이라고 판단되는 선택을 하고 그 선택을 기반으로 문제를 해결하는 방식.
동적 프로그래밍(DP): 문제를 작은 부분 문제로 나누고 그 결과를 저장하여 중복 계산을 피하며 최적해를 찾는 방식.

최적화 알고리즘의 주요 특징

탐색 공간 축소
최적화 알고리즘은 모든 경우의 수를 탐색하지 않고, 효율적으로 해를 찾기 위해 탐색 공간을 축소합니다.
- 백트래킹: 비효율적인 경로를 조기에 배제해 탐색 공간을 줄입니다.
- 그리디: 매번 가장 작은 비용이나 최대 이익을 선택해 빠르게 해를 찾습니다.
- 동적 프로그래밍: 부분 문제의 결과를 저장하여 중복된 계산을 줄임으로써 성능을 최적화합니다.
해의 최적성 보장 여부
최적화 알고리즘은 해의 최적성 보장 여부가 다릅니다.
- 백트래킹과 동적 프로그래밍: 가능한 모든 경로를 탐색하거나, 문제를 나누어 최적해를 보장합니다.
- 그리디: 매 순간 최선의 선택을 하지만, 그 선택이 전체적으로 최적해를 보장하지는 않습니다.
문제 유형에 맞는 최적화 방식
각 최적화 기법은 문제 유형에 따라 적합한 방식이 다릅니다.
- 백트래킹: 모든 해를 탐색해야 할 때 적합하며, 주로 조합 탐색이나 경로 탐색 문제에 자주 사용됩니다.
- 그리디: 각 단계에서 내리는 선택이 최종적으로도 최적해로 이어질 때 효과적입니다.
  - 예를 들어, 최소 신장 트리, 최단 경로 문제에서 많이 사용됩니다.
- 동적 프로그래밍: 문제를 작은 문제로 분할하고 이전 결과를 재사용할 수 있는 구조일 때 매우 효율적입니다.
  - 대표적으로 최적 부분 구조를 가진 문제에 자주 적용됩니다.

이번 포스팅에서는 대표적인 최적화 방식 중에서 Greedy 알고리즘에 대해서 다루어 보고자 합니다.

2. Greedy 알고리즘이란?

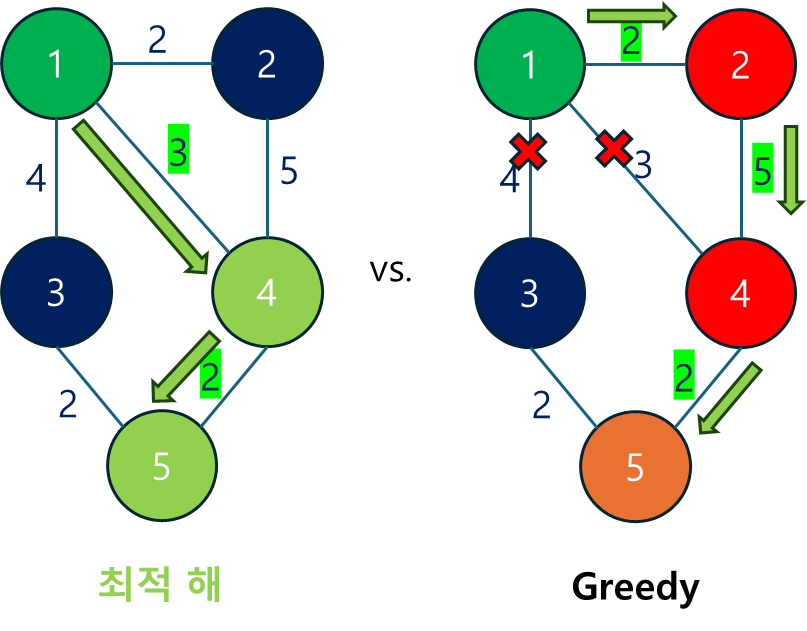
Greedy 알고리즘은 매 단계에서 가장 최적이라고 생각되는 선택을 함으로써 문제를 해결하는 방법론입니다.

즉, 각 순간에 가장 좋다고 판단되는 선택을 하고, 이를 반복하여 최종적인 해에 도달하는 방식입니다.
그리디 알고리즘의 기본 개념은 지역적으로 최적의 선택이 쌓여서 전체적으로도 최적의 해에 도달할 것이라는 가정에 기반합니다.

2.1 Greedy 알고리즘의 주요 특징

단순성
- 그리디 알고리즘은 매 단계에서의 의사결정이 매우 간단합니다.
- 복잡한 계획 없이도 현재 상태에서 가장 좋은 선택을 반복적으로 수행하는 방식이기 때문에 구현이 직관적이고 간단합니다.
빠른 계산
- 각 단계에서의 선택이 독립적이므로, 빠르게 의사결정을 할 수 있습니다.
- 이는 그리디 알고리즘이 상대적으로 시간 복잡도가 낮고 빠른 계산을 필요로 하는 문제에서 유용한 이유입니다.
전역 최적화 보장은 아님
- 중요한 점은, 그리디 알고리즘은 매번 지역적으로 최적의 선택을 하지만, 전체적으로 최적해를 보장하지는 않을 수 있다는 것입니다.
- 즉, 그리디 방법이 항상 전역 최적화를 보장하는 것은 아니며, 문제의 특성에 따라 최적해를 찾지 못할 수도 있습니다.
문제의 특성에 맞는 최적화
- 그리디 알고리즘이 적합한 문제는 "최적 부분 구조"와 "탐욕적 선택 속성"을 만족해야 합니다.
  - 최적 부분 구조: 부분 문제의 최적해가 전체 문제의 최적해로 이어질 때 그리디 알고리즘이 적합합니다.
    - 즉, 문제를 작은 문제로 나눠도 각 작은 문제에서의 최적 선택이 전체 문제의 최적 선택과 일치해야 합니다.
  - 탐욕적 선택 속성: 한번 내린 선택이 이후의 선택에 영향을 주지 않고, 그 선택이 전체 문제 해결에 유효할 때 사용됩니다.
    - 즉, 매 순간의 선택이 전체적인 해결책에 영향을 미치지 않도록 독립적이어야 합니다.

2.2 Greedy 알고리즘 적합성 판단 예시

예시: 거스름돈 문제의 그리디 알고리즘 적합성

거스름돈 문제는 그리디 알고리즘의 대표적인 예입니다.
- 예를 들어, 동전 단위가 [1, 5, 10, 50, 100]일 때, 그리디 알고리즘은 가장 큰 동전부터 선택해도 항상 최적의 해를 보장합니다.
  - 이 경우, 큰 동전부터 선택하면 남은 금액도 적은 동전들로 정확하게 거슬러 줄 수 있습니다.
  - 예를 들어, 87원을 거슬러 줄 때, 50원, 10원, 10원, 10원, 5원, 1원, 1원을 순서대로 선택하면 정확한 해가 됩니다.
  - 이는 각 동전이 이전 동전의 배수이기 때문에, 부분 문제의 최적해가 전체 문제의 최적해로 자연스럽게 이어지기 때문입니다.
- 그러나 동전 단위가 [1, 4, 5, 10, 40, 50, 100]과 같은 경우, 그리디 알고리즘은 항상 최적해를 보장하지 못할 수 있습니다.
  - 예를 들어, 8원을 거슬러 줄 때 그리디 알고리즘은 5원을 먼저 선택하고, 나머지 3원을 거슬러 주려고 1원을 세 번 선택합니다. 결과적으로 4개의 동전이 필요합니다.
  - 하지만 최적의 방법은 4원을 두 번 선택하는 것이며, 이 경우에는 2개의 동전만으로 해결할 수 있습니다.
  - 이는 큰 단위를 먼저 선택하는 방식이 항상 전체적으로 최적이 되지 않을 수 있음을 보여줍니다.
그래서 그리디 알고리즘은 매 순간의 선택으로 최적의 해를 구할 수 있는 경우에 쓰이는 것이 좋고, 그렇지 못한 경우엔 다른 최적화 알고리즘을 고려해보는 것이 좋습니다.

거스름돈 예시에 대한 내용은 다음 파트에서 더 자세히 다루도록 하겠습니다.

2.3 Greedy 알고리즘의 한계

그리디 알고리즘은 빠르게 해를 찾는 장점이 있지만, 항상 최적해를 보장하지 않기 때문에 적용하는 문제의 특성에 따라 신중한 선택이 필요합니다.
문제에 따라 그리디 알고리즘이 아닌 다른 최적화 기법, 예를 들어 동적 프로그래밍이나 백트래킹이 더 나은 해법이 될 수 있습니다.

결론적으로, 그리디 알고리즘은 매 순간의 선택이 전체 문제의 최적해로 이어질 수 있는 문제에 효과적이며, 그렇지 않은 경우엔 다른 최적화 기법이 필요할 수 있습니다.

3. Greedy 알고리즘 활용 예시

Greedy 알고리즘은 여러 문제에 적용될 수 있으며, 특히 최소 비용을 구하는 문제나 최대 이익을 구하는 문제에서 효과적으로 사용됩니다.

가장 대표적인 그리디 알고리즘의 활용 예시로 거스름돈 문제와 활동 선택 문제를 Java와 Python 코드로 각각 구현해보겠습니다.

3.1 예시 1: 거스름돈 문제 (Coin Change Problem)

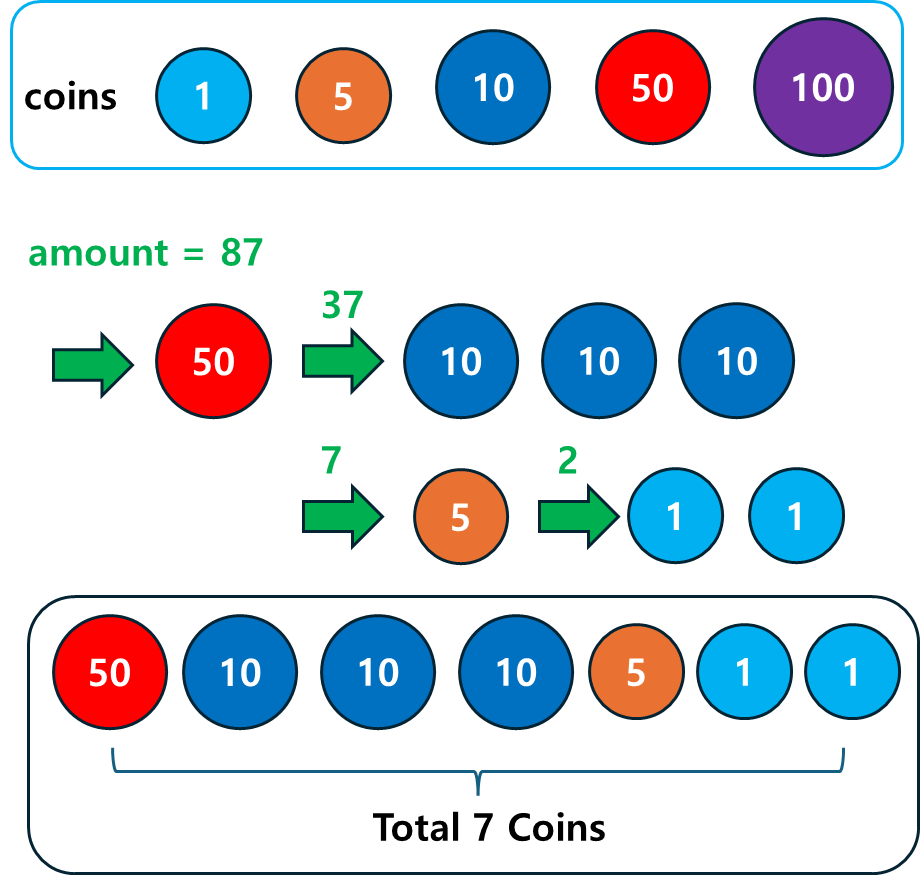
문제: 거스름돈을 최소 개수의 동전으로 줄 수 있는 방법을 찾아보자.

동전 단위는 [1, 5, 10, 50, 100]으로 가정합니다.

Java 코드

import java.util.Arrays;

public class CoinChangeGreedy {
    public static void main(String[] args) {
        int[] coins = {1, 5, 10, 50, 100};
        int amount = 87;
        
        int result = coinChange(coins, amount);
        System.out.println("필요한 최소 동전 개수: " + result);
    }

    public static int coinChange(int[] coins, int amount) {
        Arrays.sort(coins);  // 동전 배열을 오름차순으로 정렬
        int count = 0;

        for (int i = coins.length - 1; i >= 0; i--) {  // 큰 동전부터 선택
            if (amount >= coins[i]) {
                count += amount / coins[i];  // 동전 개수 추가
                amount %= coins[i];  // 남은 금액 갱신
            }
        }
        return count;
    }
}

Python 코드

def coin_change(coins, amount):
    coins.sort(reverse=True)  # 동전 배열을 내림차순으로 정렬
    count = 0
    
    for coin in coins:
        if amount >= coin:
            count += amount // coin  # 동전 개수 추가
            amount %= coin  # 남은 금액 갱신

    return count

coins = [1, 5, 10, 50, 100]
amount = 87

result = coin_change(coins, amount)
print(f"필요한 최소 동전 개수: {result}")

- 출력 결과 (Java, Python 동일)

필요한 최소 동전 개수: 7

설명:

위 코드는 큰 단위의 동전부터 선택하는 그리디 방식으로 거스름돈 문제를 해결합니다.

87원을 거슬러 줄 때, 큰 동전부터 선택하여 동전 개수를 최소화하여 7개라는 답을 얻습니다.

3.2 예시 2: 활동 선택 문제 (Activity Selection Problem)

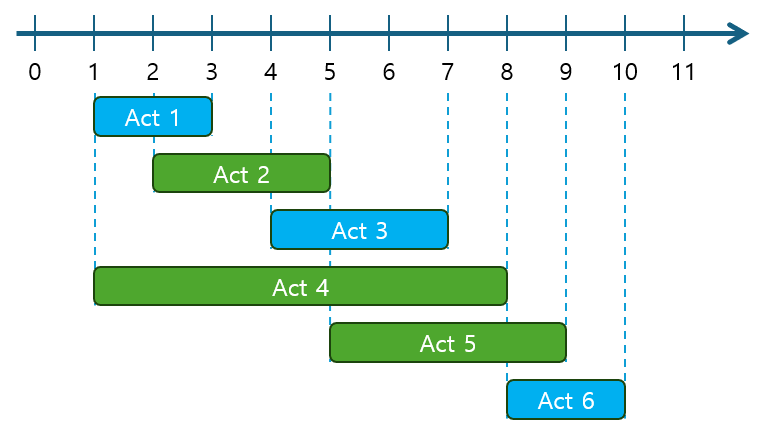
문제: 여러 활동들이 시작 시간과 종료 시간이 주어졌을 때, 서로 겹치지 않게 가장 많은 활동을 선택하는 방법을 찾아보자.

Java 코드

import java.util.Arrays;
import java.util.Comparator;

public class ActivitySelection {
    public static void main(String[] args) {
        int[][] activities = {{1, 3}, {2, 5}, {4, 7}, {1, 8}, {5, 9}, {8, 10}};
        
        int maxActivities = activitySelection(activities);
        System.out.println("선택할 수 있는 최대 활동 개수: " + maxActivities);
    }

    public static int activitySelection(int[][] activities) {
        // 종료 시간을 기준으로 활동 정렬
        Arrays.sort(activities, Comparator.comparingInt(a -> a[1]));
        
        int count = 1;  // 첫 번째 활동은 항상 선택
        int lastEnd = activities[0][1];  // 첫 번째 활동의 종료 시간
        
        for (int i = 1; i < activities.length; i++) {
            if (activities[i][0] >= lastEnd) {  // 현재 활동의 시작 시간이 이전 활동의 종료 시간 이후라면 선택
                count++;
                lastEnd = activities[i][1];  // 마지막 선택한 활동의 종료 시간 갱신
            }
        }
        return count;
    }
}

Python 코드

def activity_selection(activities):
    # 종료 시간을 기준으로 활동 정렬
    activities.sort(key=lambda x: x[1])
    
    count = 1  # 첫 번째 활동 선택
    last_end = activities[0][1]  # 첫 번째 활동의 종료 시간
    
    for i in range(1, len(activities)):
        if activities[i][0] >= last_end:  # 다음 활동이 마지막 선택된 활동 이후에 시작하는 경우
            count += 1
            last_end = activities[i][1]  # 종료 시간 갱신

    return count

activities = [(1, 3), (2, 5), (4, 7), (1, 8), (5, 9), (8, 10)]

result = activity_selection(activities)
print(f"선택할 수 있는 최대 활동 개수: {result}")

- 출력 결과 (Java, Python 동일)

선택할 수 있는 최대 활동 개수: 3

설명:

위 코드는 종료 시간을 기준으로 활동을 정렬한 후, 그리디 방식으로 가장 많은 활동을 선택하는 방법을 구현한 것입니다.

종료 시간이 빠른 활동을 먼저 선택하는 방식은 탐욕적 선택 속성을 충족하여 최적해를 보장합니다.

4. Greedy 알고리즘의 복잡도

4.1 시간 복잡도

그리디 알고리즘의 시간 복잡도는 문제의 특성에 따라 달라집니다.
- 보통 정렬이 필요한 문제가 많기 때문에 정렬의 시간 복잡도가 전체 알고리즘의 주요 요소로 작용합니다.
예시 1: 거스름돈 문제
- 동전 단위가 정렬되어 있는 경우, 각 동전을 선택하는 과정은 상수 시간이므로 시간 복잡도는 O(n)입니다. 여기서 n은 동전의 개수입니다.
예시 2: 활동 선택 문제
- 활동의 종료 시간을 기준으로 정렬하는 과정이 O(n log n)의 시간 복잡도를 가집니다. 이후 선택하는 과정은 O(n)이므로, 전체 시간 복잡도는 O(n log n)이 됩니다.

4.2 공간 복잡도

Greedy 알고리즘은 보통 추가적인 메모리 사용이 적기 때문에 대부분 O(1)의 공간 복잡도를 가집니다.

다만, 입력 데이터의 크기에 따라 공간 복잡도가 O(n)이 될 수 있습니다.

마무리

이번 포스팅에서는 Greedy 알고리즘의 개념과 특징들을 살펴보았고, 거스름돈 문제와 활동 선택 문제를 통해 그리디 알고리즘의 작동 원리와 적용 방법을 살펴보았습니다.

Greedy 알고리즘은 매 순간의 선택을 통해 빠르고 효율적으로 문제를 해결하는 방식으로, 특히 최소 비용이나 최대 이익을 구하는 문제에서 효과적입니다.
그리디 알고리즘은 간단한 구현과 빠른 계산 속도로 다양한 문제에 많이 적용되지만, 항상 최적해를 보장하지는 않기 때문에 문제의 특성에 따라 신중한 선택이 필요합니다.

다음 포스팅에서는 동적 프로그래밍(DP)을 다루겠습니다.

동적 프로그래밍은 중복된 계산을 방지하고, 부분 문제의 결과를 저장하여 효율적으로 문제를 해결하는 알고리즘으로, 그리디 알고리즘과는 다른 방식으로 최적해를 구하는 방법을 제공합니다.
다음 포스팅에서 동적 프로그래밍의 개념과 실습을 통해 문제를 해결하는 방법을 함께 알아보겠습니다.