본 시리즈는 프로그래밍 알고리즘의 개념을 정리하고 실습을 진행해보는 시리즈입니다.

• 실습은 다음과 같은 개발환경 및 버전에서 진행하였습니다.
  • IDE : IntelliJ IDEA (Ultimate Edition)
  • Java : JDK 21 (corretto-21)
  • Python : 3.9 (conda env)

탐색(Search) - BackTracking

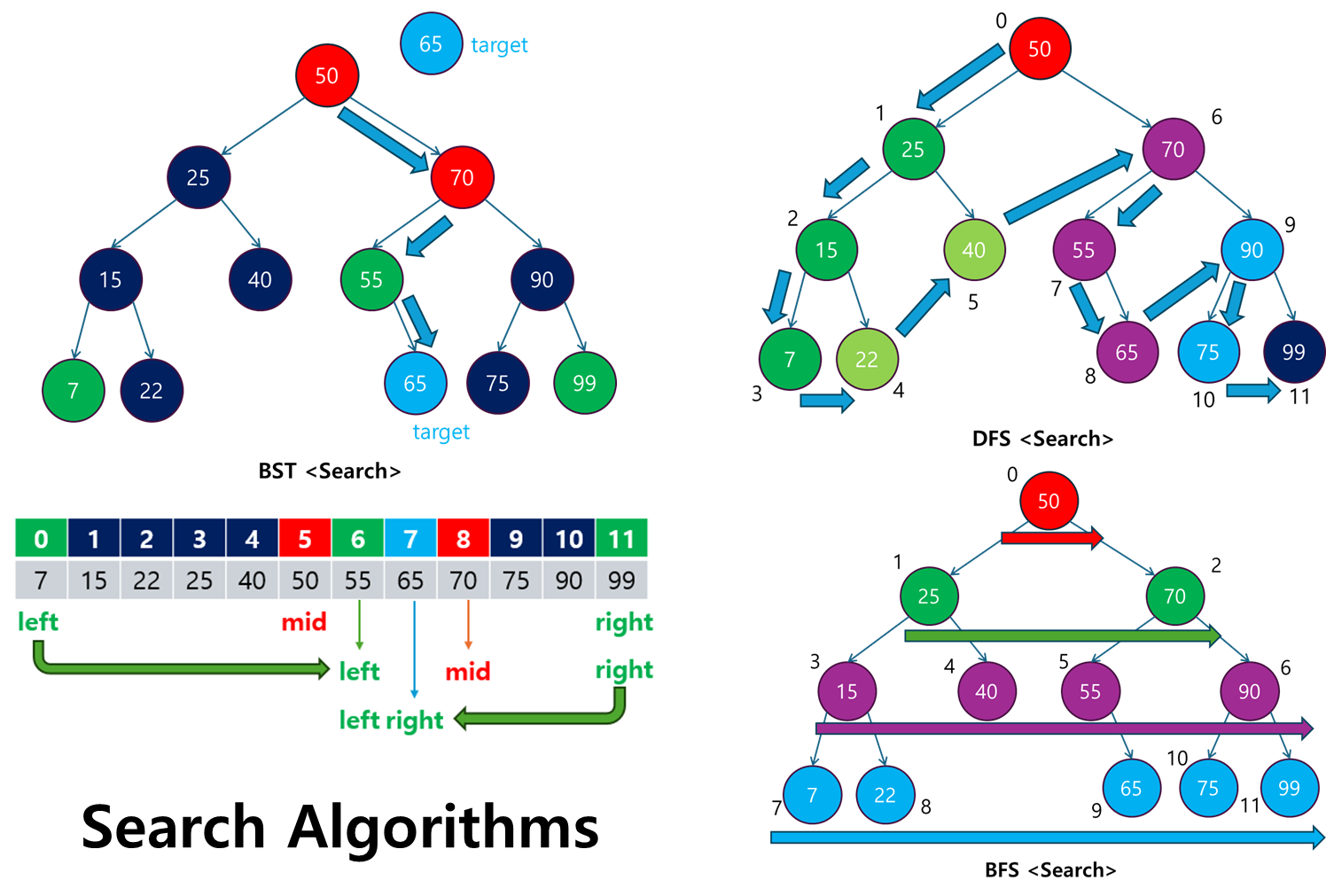
1. 탐색(Search) 알고리즘이란?

탐색(Search) 알고리즘은 주어진 데이터 구조 내에서 원하는 데이터를 찾아내기 위한 일련의 과정입니다.

• 배열, 트리, 그래프와 같은 자료구조에서 특정 값을 찾거나, 문제에서 요구하는 조건에 맞는 해답을 도출할 때 사용됩니다.
• 효율적인 탐색 알고리즘을 활용하면 시간과 자원을 절약할 수 있으며, 특히 데이터의 규모가 커질수록 그 중요성이 커집니다.

탐색 알고리즘은 크게 두 가지 범주로 나눌 수 있습니다:

1. 배열 기반 탐색
   배열을 기반으로 원하는 값을 찾거나 조건을 만족하는 요소를 탐색하는 알고리즘입니다.

• 선형 탐색(Linear Search): 배열을 처음부터 끝까지 하나씩 살펴보며 찾는 방식. 가장 기본적인 탐색 방법이지만, 속도가 느립니다.
• 이진 탐색(Binary Search): 정렬된 배열에서 중간 값을 기준으로 탐색 범위를 절반으로 좁혀가며 찾는 방식. 시간 복잡도가 O(log n)으로 매우 효율적입니다.
• 투 포인터(Two-Pointer): 배열의 양쪽 끝에서 시작해 조건을 만족할 때까지 포인터를 조정하는 방식. 주로 정렬된 배열에서 두 수의 합 등을 찾는 문제에 사용됩니다.

2. 그래프 및 트리 기반 탐색
   트리나 그래프와 같은 비선형 자료구조에서 특정 값을 찾는 알고리즘입니다.

• 깊이 우선 탐색(DFS): 한 경로를 끝까지 탐색한 후, 다른 경로로 백트래킹하며 탐색하는 방식. 순환 구조나 경로 찾기 문제에 유용합니다.
• 너비 우선 탐색(BFS): 시작 지점에서 가까운 노드를 먼저 탐색하며 점진적으로 넓혀가는 방식. 최단 경로 탐색 문제에 적합합니다.
• 백트래킹(Backtracking): 가능한 모든 경로를 탐색하되, 유망하지 않은 경로는 중간에 포기하는 방식. 그래프나 트리뿐만 아니라 배열에서 순열, 조합, 부분집합을 찾는 문제에도 자주 사용됩니다.

이번 시리즈에서는 이러한 다양한 탐색 알고리즘을 순차적으로 다루면서 그 개념과 활용 방법을 소개합니다.

이번 포스팅에서는 백트래킹(Backtracking)을 중점적으로 다루도록 하겠습니다.

2. Backtracking이란?

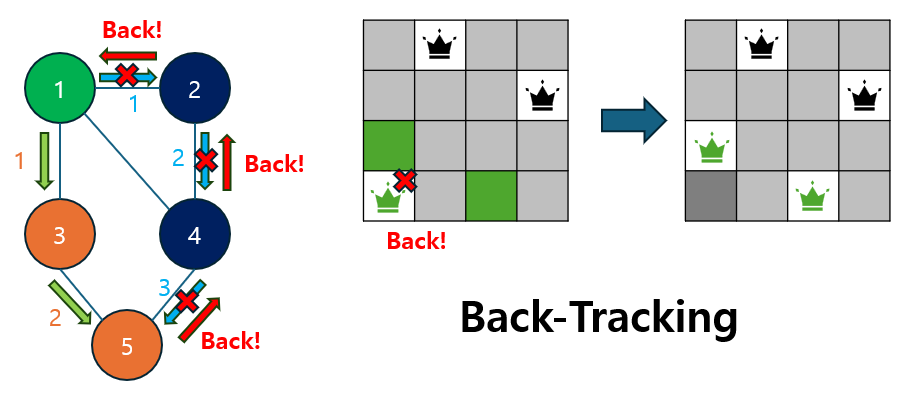
백트래킹(Backtracking)은 해를 찾기 위해 모든 가능한 경우의 수를 탐색하는 기법 중 하나로, 조건에 맞지 않는 해를 도중에 포기하고 다른 경로를 탐색하는 방식입니다.

• 즉, 일종의 브루트 포스(Brute Force) 방식이지만, 불필요한 경로는 중간에 탐색을 중단하여 탐색 효율성을 높이는 기법입니다.

2.1 Backtracking의 특징

백트래킹은 다음과 같은 특징을 가지고 있습니다:

1. 탐색 과정 중 실패 가능성: 특정 경로가 문제의 해답이 될 수 없음을 알게 되면, 그 경로의 탐색을 즉시 중단하고 다른 경로를 탐색합니다. 이 과정을 백트래킹이라고 부르며, 이는 마치 길을 잘못 들었을 때 다시 돌아와 새로운 길을 찾는 것과 유사합니다.

2. 재귀적 탐색: 백트래킹은 주로 재귀적으로 구현되며, 문제를 작은 부분으로 나누어 하위 문제를 해결하고, 조건에 맞지 않으면 다시 돌아와 다른 하위 문제를 탐색합니다.

3. 최적화 및 탐색 문제: 백트래킹은 최적화 문제와 탐색 문제에 적합합니다. 특히, 해의 구조가 나뉘는 문제에 매우 적합하며, N-Queen 문제, 미로 탐색, 순열과 조합 등에서 자주 사용됩니다.

백트래킹의 탐색 방식은 깊이 우선 탐색(DFS)과 유사하지만, 가능성이 없는 경로는 중간에 포기한다는 점에서 차이가 있습니다.

• 백트래킹은 해답 공간을 빠르게 줄이기 위해 가지치기(Pruning) 기법을 사용합니다.
• 이는 불필요한 경로를 더 이상 탐색하지 않도록 하여, 시간 복잡도를 줄이는 데 도움을 줍니다.

2.2 Backtracking의 작동 과정

1. 해당 상태가 유망한지 확인: 문제의 특정 상태가 조건을 만족하는지 확인합니다.
2. 유망하지 않은 경우 백트래킹: 조건을 만족하지 않으면, 더 깊이 탐색하지 않고 다시 돌아가 다른 경로를 선택합니다.
3. 모든 경로를 탐색할 때까지 반복: 조건을 만족하는 해가 나올 때까지 이 과정을 계속 반복합니다.

2.3 대표적인 예시:

• N-Queen 문제: 체스판 위에서 N개의 퀸이 서로 공격하지 않도록 배치하는 문제입니다.
  • 각 퀸이 같은 행, 열, 대각선에 위치하지 않도록 조건을 검사하며, 조건을 만족하지 않으면 마지막 배치를 되돌려 퀸을 다시 배치합니다.
• 미로 찾기: 미로에서 출구를 찾는 문제에서, 벽에 막히면 다시 이전 위치로 돌아가 다른 경로를 탐색합니다.

백트래킹은 이처럼 경로가 올바르지 않다면 되돌아가서 다른 경로를 찾는 것을 기본으로 하며, 탐색 효율성을 극대화하는 데 주로 사용됩니다.

3. Backtracking 활용 예시

Backtracking 알고리즘은 모든 가능한 해를 탐색하되, 유망하지 않은 경로를 빠르게 제외함으로써 탐색 범위를 줄이는 방식입니다. 이 방식은 순열, 조합, 또는 최적화 문제와 같은 경우에 유용하게 사용됩니다.

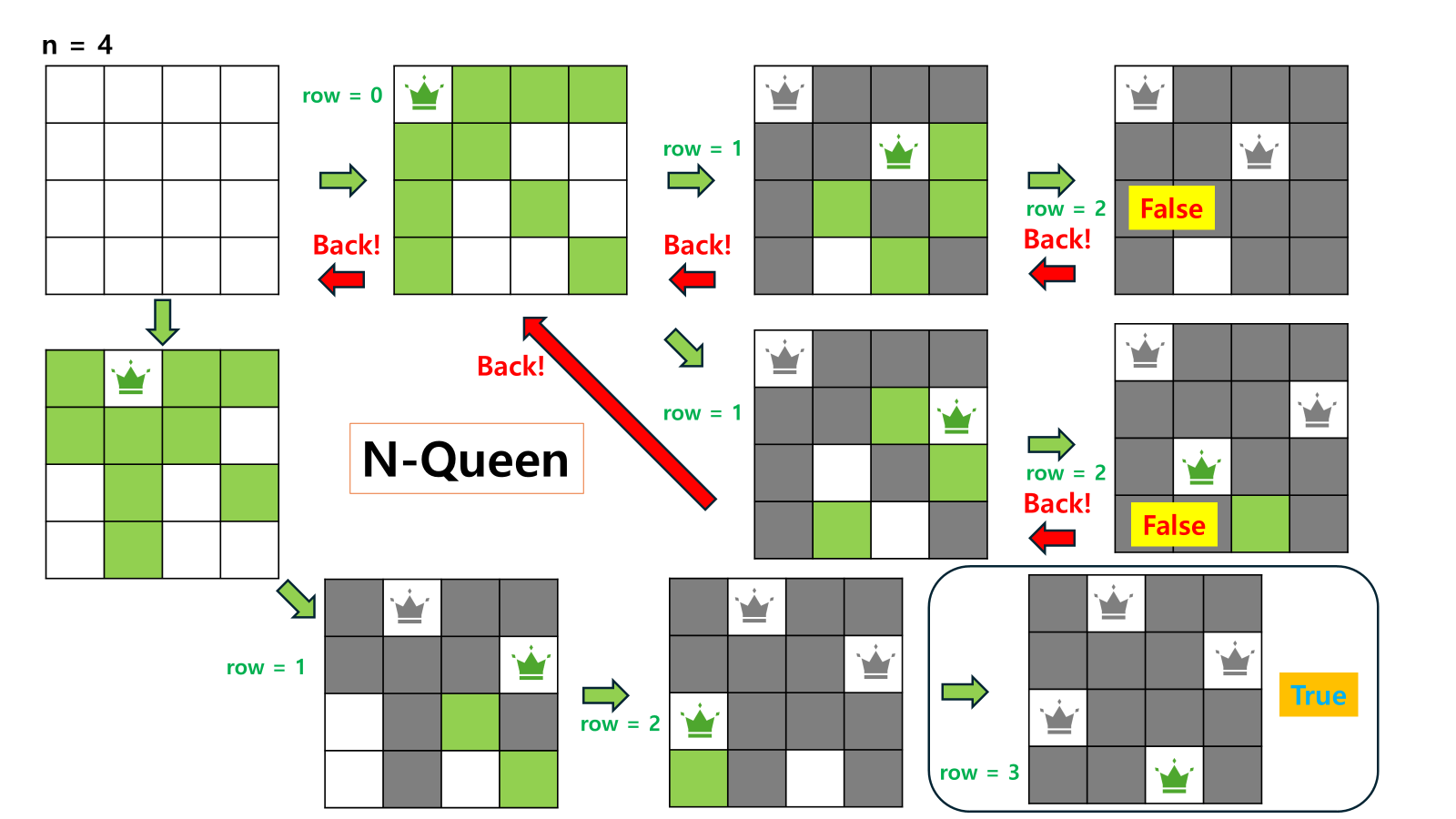
3.1 N-Queen 문제

N-Queen 문제는 대표적인 Backtracking 알고리즘의 예시로, N x N 체스판 위에 N개의 퀸(Queen)을 서로 공격할 수 없도록 배치하는 문제입니다.

• 퀸은 행, 열, 대각선으로 이동할 수 있기 때문에, 하나의 퀸이 위치한 행과 열, 그리고 대각선에는 다른 퀸을 배치할 수 없습니다.
• 따라서 Backtracking을 사용하여 퀸을 한 행씩 배치하면서 유효한지 검토하고, 유효하지 않으면 다시 돌아가 다른 경로를 탐색합니다.

Python 코드 구현:

def is_safe(board, row, col, n):
    # 같은 열에 퀸이 있는지 확인
    for i in range(row):
        if board[i][col] == 1:
            return False
    
    # 왼쪽 대각선 위에 퀸이 있는지 확인
    for i, j in zip(range(row, -1, -1), range(col, -1, -1)):
        if board[i][j] == 1:
            return False
    
    # 오른쪽 대각선 위에 퀸이 있는지 확인
    for i, j in zip(range(row, -1, -1), range(col, n)):
        if board[i][j] == 1:
            return False
    
    return True

def solve_n_queens(board, row, n):
    if row >= n:
        # 퀸이 모두 배치된 경우, 결과 출력
        for line in board:
            print(line)
        print()
        return True
    
    result = False
    for col in range(n):
        if is_safe(board, row, col, n):
            board[row][col] = 1  # 퀸 배치
            result = solve_n_queens(board, row + 1, n) or result
            board[row][col] = 0  # Backtracking
    
    return result

# N-Queen 문제 실행 (N=4)
n = 4
board = [[0 for _ in range(n)] for _ in range(n)]
solve_n_queens(board, 0, n)

• 출력 결과

[0, 1, 0, 0]
[0, 0, 0, 1]
[1, 0, 0, 0]
[0, 0, 1, 0]

[0, 0, 1, 0]
[1, 0, 0, 0]
[0, 0, 0, 1]
[0, 1, 0, 0]

위 코드에서는 재귀를 사용해 각 행에 퀸을 배치한 후, 유효하지 않으면 다시 퀸을 제거하고 다른 경로를 탐색하는 방식입니다.

Java 코드 구현:

public class NQueens {
    private static boolean isSafe(int[][] board, int row, int col, int n) {
        // 같은 열에 퀸이 있는지 확인
        for (int i = 0; i < row; i++) {
            if (board[i][col] == 1) {
                return false;
            }
        }

        // 왼쪽 대각선 위에 퀸이 있는지 확인
        for (int i = row, j = col; i >= 0 && j >= 0; i--, j--) {
            if (board[i][j] == 1) {
                return false;
            }
        }

        // 오른쪽 대각선 위에 퀸이 있는지 확인
        for (int i = row, j = col; i >= 0 && j < n; i--, j++) {
            if (board[i][j] == 1) {
                return false;
            }
        }

        return true;
    }

    private static boolean solveNQueens(int[][] board, int row, int n) {
        if (row >= n) {
            printSolution(board, n);
            return true;
        }

        boolean result = false;
        for (int col = 0; col < n; col++) {
            if (isSafe(board, row, col, n)) {
                board[row][col] = 1;  // 퀸 배치
                result = solveNQueens(board, row + 1, n) || result;
                board[row][col] = 0;  // Backtracking
            }
        }
        return result;
    }

    private static void printSolution(int[][] board, int n) {
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                System.out.print(board[i][j] + " ");
            }
            System.out.println();
        }
        System.out.println();
    }

    public static void main(String[] args) {
        int n = 4;  // N-Queen 문제 (N=4)
        int[][] board = new int[n][n];
        solveNQueens(board, 0, n);
    }
}

• 출력 결과

0 1 0 0 
0 0 0 1 
1 0 0 0 
0 0 1 0 

0 0 1 0 
1 0 0 0 
0 0 0 1 
0 1 0 0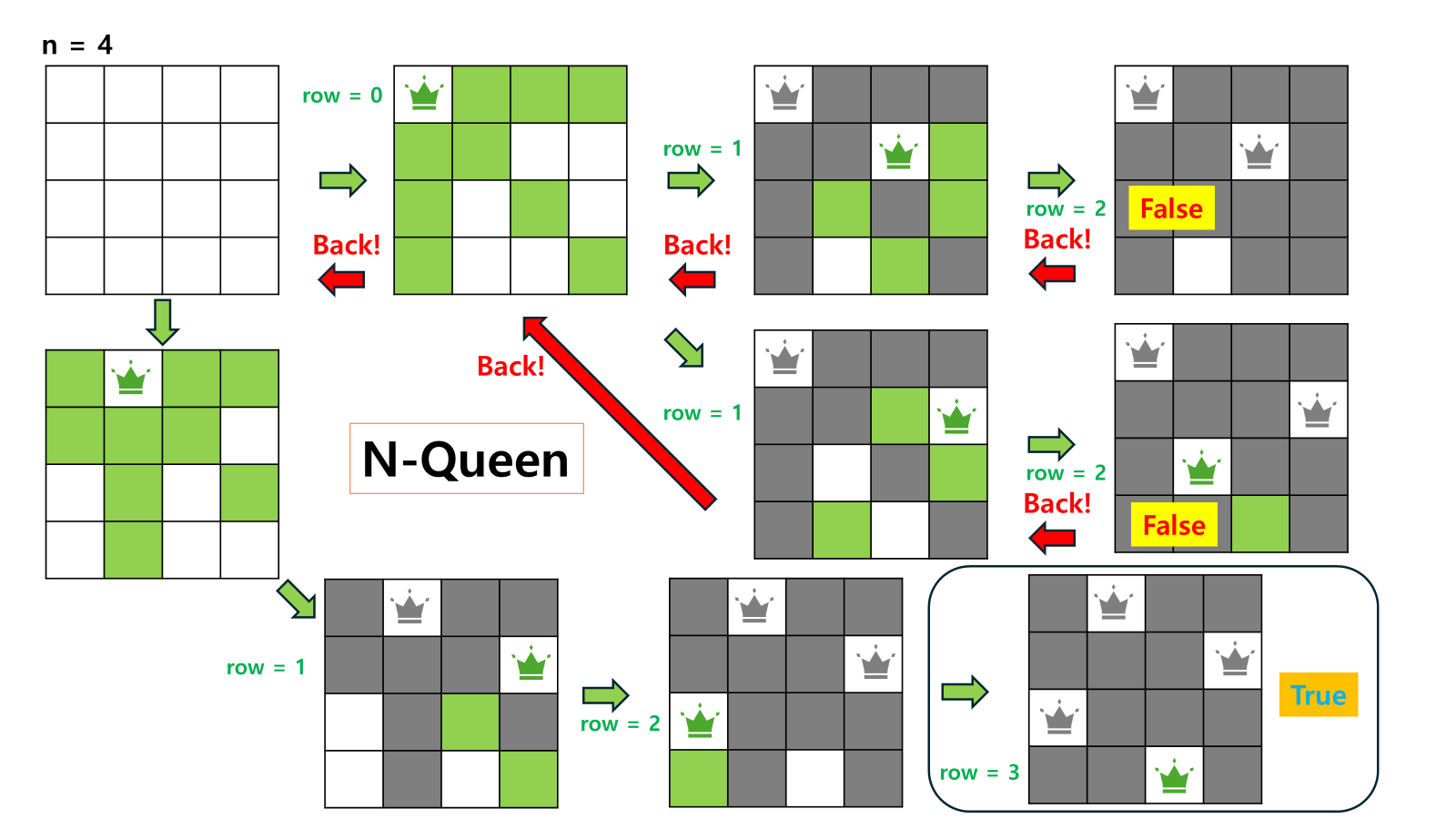 

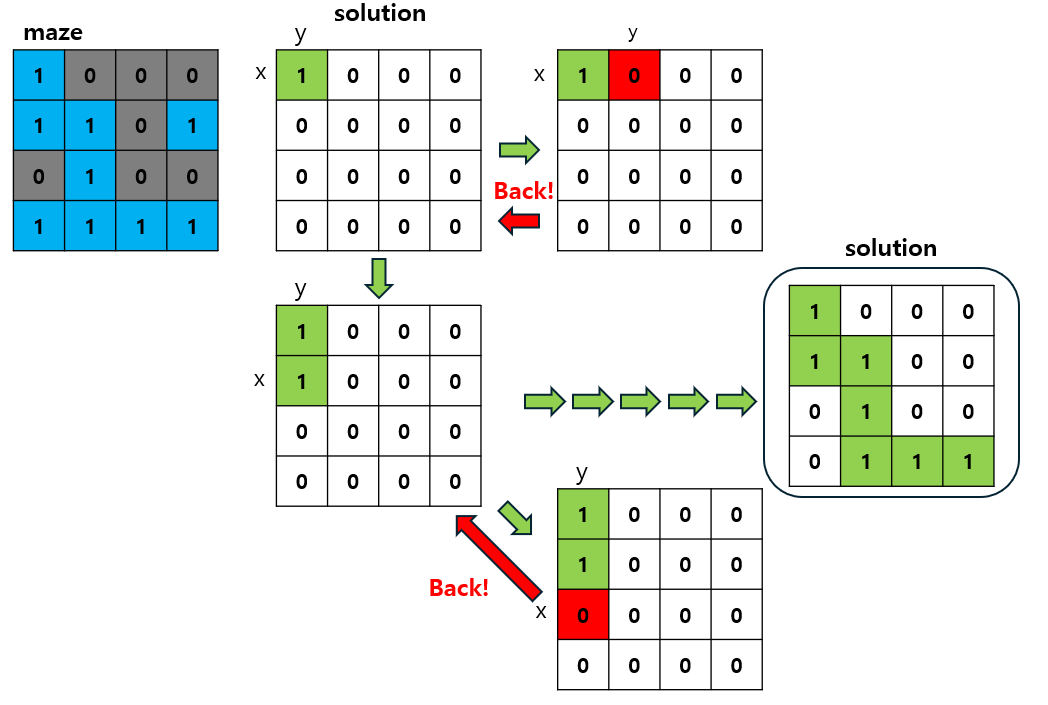
3.2 최단 경로 문제 (Shortest Path)

Backtracking은 최단 경로 문제에서도 사용할 수 있습니다.

• 예를 들어, 미로 탐색 문제에서 시작점에서 도착점까지의 최단 경로를 찾는 문제를 해결할 수 있습니다.
• Backtracking을 통해 유망하지 않은 경로는 빠르게 포기하고 다른 경로를 탐색하여 최적의 해를 찾습니다.

Python 코드 구현:

def is_safe(maze, x, y, solution):
    # 좌표가 미로 범위 안에 있는지 먼저 확인
    if not (0 <= x < len(maze) and 0 <= y < len(maze)):
        return False

    # 그 후에 통로인지 확인 (1이면 통로, 0이면 벽)
    if maze[x][y] != 1:
        return False

    # 마지막으로 해당 좌표가 아직 방문되지 않았는지 확인
    if solution[x][y] != 0:
        return False

    return True

def solve_maze(maze):
    n = len(maze)
    solution = [[0 for _ in range(n)] for _ in range(n)]

    if solve_maze_util(maze, 0, 0, solution):
        for line in solution:
            print(line)
    else:
        print("No solution exists")

def solve_maze_util(maze, x, y, solution):
    if x == len(maze) - 1 and y == len(maze) - 1:
        solution[x][y] = 1
        return True

    if is_safe(maze, x, y, solution):
        solution[x][y] = 1

        if solve_maze_util(maze, x + 1, y, solution):
            return True
        if solve_maze_util(maze, x, y + 1, solution):
            return True

        solution[x][y] = 0  # Backtracking
        return False
    return False

# 테스트용 미로 (1: 통로, 0: 벽)
maze = [
    [1, 0, 0, 0],
    [1, 1, 0, 1],
    [0, 1, 0, 0],
    [1, 1, 1, 1]
]

solve_maze(maze)

• 출력

[1, 0, 0, 0]
[1, 1, 0, 0]
[0, 1, 0, 0]
[0, 1, 1, 1]

Java 코드 구현:

public class MazeSolver {
    private static boolean isSafe(int[][] maze, int x, int y, int[][] solution) {
        return x >= 0 && 
                x < maze.length && 
                y >= 0 && y < maze[0].length && 
                maze[x][y] == 1 && solution[x][y] == 0;
    }

    public static void solveMaze(int[][] maze) {
        int n = maze.length;
        int[][] solution = new int[n][n];

        if (solveMazeUtil(maze, 0, 0, solution)) {
            printSolution(solution);
        } else {
            System.out.println("No solution exists");
        }
    }

    private static boolean solveMazeUtil(int[][] maze, int x, int y, int[][] solution) {
        if (x == maze.length - 1 && y == maze.length - 1) {
            solution[x][y] = 1;
            return true;
        }

        if (isSafe(maze, x, y, solution)) {
            solution[x][y] = 1;

            if (solveMazeUtil(maze, x + 1, y, solution)) {
                return true;
            }
            if (solveMazeUtil(maze, x, y + 1, solution)) {
                return true;
            }

            solution[x][y] = 0;  // Backtracking
            return false;
        }
        return false;
    }

    private static void printSolution(int[][] solution) {
        for (int[] row : solution) {
            for (int cell : row) {
                System.out.print(cell + " ");
            }
            System.out.println();
        }
    }

    public static void main(String[] args) {
        int[][] maze = {
            {1, 0, 0, 0},
            {1, 1, 0, 1},
            {0, 1, 0, 0},
            {1, 1, 1, 1}
        };
        solveMaze(maze);
    }
}

• 출력

1 0 0 0 
1 1 0 0 
0 1 0 0 
0 1 1 1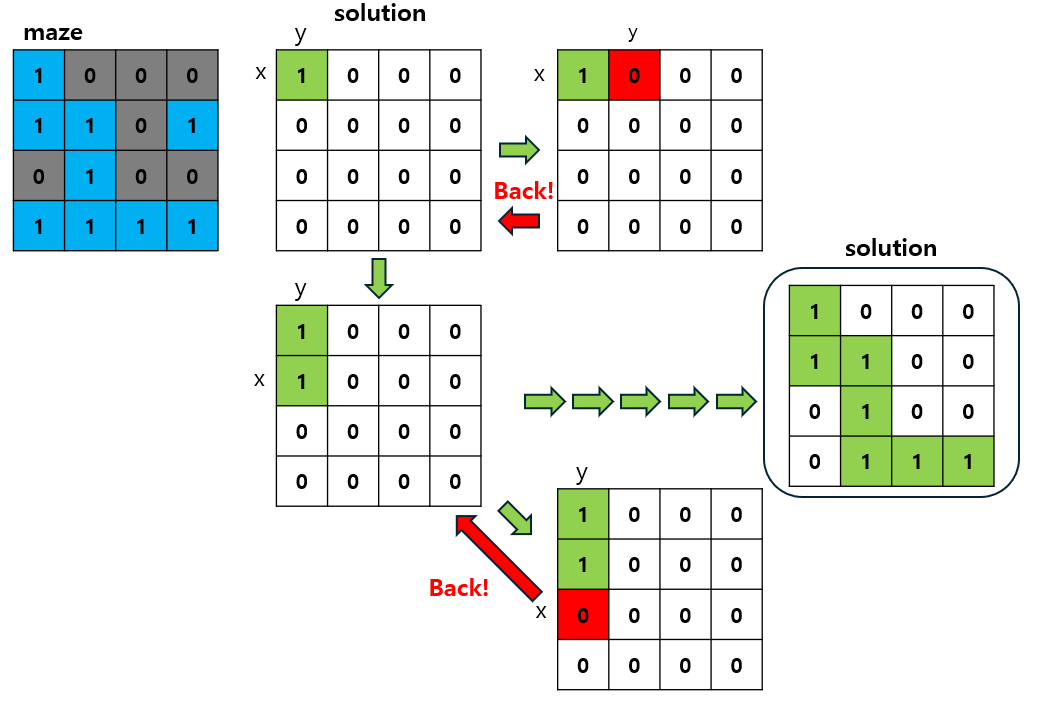 

4. Backtracking 알고리즘의 복잡도

백트래킹(Backtracking) 알고리즘은 재귀적으로 모든 가능한 해를 탐색하되, 유망하지 않은 경로는 중간에 탐색을 중단하여 효율성을 높입니다.

• 이러한 방식으로 동작하는 백트래킹은 경우에 따라 탐색 범위를 줄여줄 수 있지만, 최악의 경우에는 여전히 모든 경우의 수를 탐색해야 합니다.

4.1 시간 복잡도

백트래킹의 시간 복잡도는 문제의 종류에 따라 달라지지만, 일반적으로 탐색해야 할 경로의 수에 비례합니다.

1. N-Queen 문제의 경우:

   • 퀸을 하나씩 배치하며 가능한 경우를 모두 탐색하므로 각 퀸에 대해 N개의 위치를 탐색하게 됩니다.
   • 최악의 경우, 모든 경로를 탐색해야 하므로 시간 복잡도는 $O(N!)$이 됩니다.
   • 그러나, 가지치기(Pruning)를 통해 일부 경로를 일찍 포기할 수 있어, 실제 수행 시간은 이보다는 줄어들 수 있습니다.

2. 미로 탐색 문제의 경우:

   • 미로의 크기를 N x N이라고 가정하면, 모든 경로를 탐색하는 최악의 경우에는 $O(2^{N²})$의 시간 복잡도가 될 수 있습니다.
   • 하지만, 백트래킹을 통해 불필요한 경로를 제외할 수 있어, 실제 수행 시간은 이보다는 줄어들 수 있습니다.

4.2 공간 복잡도

백트래킹의 공간 복잡도는 일반적으로 재귀 깊이에 따라 달라집니다.

1. N-Queen 문제의 경우:

   • 재귀 호출이 최대 N번 발생할 수 있으므로, 공간 복잡도는 O(N)입니다.

2. 미로 탐색 문제의 경우:

   • 탐색하는 미로의 크기가 N x N일 때, 공간 복잡도는 O(N²)입니다. 이는 경로를 추적하기 위해 사용하는 solution 배열과 재귀 호출 스택의 깊이에 따라 달라집니다.

4.3 최적화 기법

백트래킹은 가지치기(Pruning)를 통해 불필요한 경로를 미리 포기함으로써 시간 복잡도를 줄일 수 있습니다. 이를 통해 탐색 범위를 줄일 수 있지만, 문제의 특성에 따라 최악의 경우에는 여전히 모든 경로를 탐색해야 합니다.

• 예를 들어, N-Queen 문제에서는 같은 열이나 대각선에 퀸이 놓일 수 없으므로, 이 조건을 미리 확인함으로써 탐색해야 할 경로의 수를 크게 줄일 수 있습니다.
• 미로 탐색 문제에서는 벽에 막히면 바로 그 경로를 포기하고 다른 경로를 탐색할 수 있습니다.

마무리

이번 포스팅에서는 백트래킹(Backtracking) 알고리즘에 대해 살펴보았습니다.

• 백트래킹은 모든 가능한 해를 탐색하는 방식이지만, 조건에 맞지 않는 경로는 중간에 탐색을 중단하여 효율성을 높이는 알고리즘입니다.

• N-Queen 문제와 미로 탐색 문제를 통해 백트래킹의 원리와 구현 방법을 살펴보았습니다.

• 백트래킹의 시간 복잡도는 문제의 특성에 따라 달라지며, 최악의 경우 모든 경로를 탐색해야 하지만, 가지치기(Pruning) 기법을 통해 일부 경로를 미리 포기할 수 있습니다.

다음 포스팅에서는 최적화 기법 중 하나인 Greedy(탐욕 알고리즘)을 다룰 예정입니다.

• 이번에 다루었던 백트래킹도 관점에 따라서 최적화 기법의 한 종류로 볼 수 있기때문에, 자연스럽게 Greedy 알고리즘과의 연결이 가능할 것입니다.
• Greedy 알고리즘은 지역 최적해를 선택하여 전역 최적해에 도달하려는 방식으로, 백트래킹과는 다른 탐색 방법을 제공합니다.