최근에 cs231n 내용을 다시 복습하면서 모르는 내용을 채워가는 중인데, 그 중에 첫 번째로 다룰 주제는 norm이다. cs231n 2강의 knn classifier의 원리를 설명하면서 나오는 내용이다. 물론 image classification에는 knn을 사용하진 않지만, 후에 regularization에서 L1,L2 norm을 이용하기 때문에, 개념을 정확히 알아둘 필요가 있다.
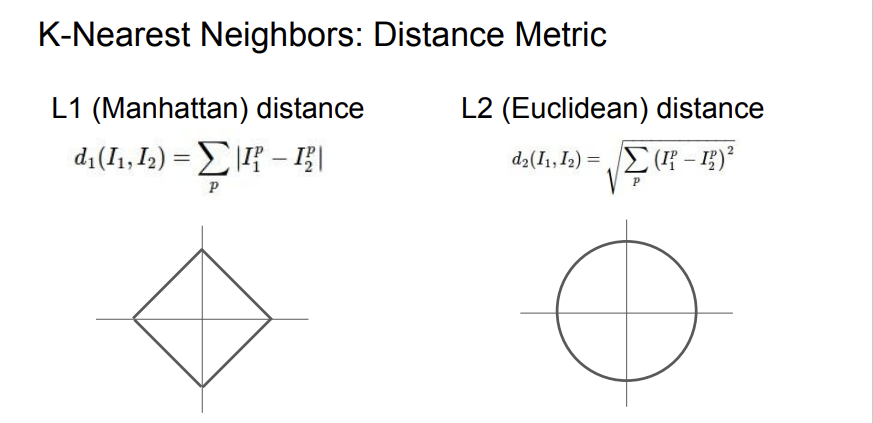
내가 이해가 안된 것은 위의 그래프 2개이다. 왜 L1이면 사각형 모양이 나오고, L2면 원이 나오는가? 가 궁금했던 것이다. 일단 norm에 대한 이해를 해보자.
1. Norm
Norm은 벡터의 크기를 나타내는 개념이다. L1, L2, 그리고 확장해서 max norm과 n차 norm까지 살펴볼텐데, 이해를 위해 예시에서는 간단한 2차원 벡터를 이용해 설명하겠다. 사용할 벡터는 A(-1,1), B(4,3) 2개이다. 각 예시에 해당하는 계산식은 아래 사진에 정리해두었다. 나는 여기서 L1,L2라고 쓰긴 했지만, 1차 놈, 2차 놈이라고 표현하기도 한다. (일반화해서 p차 놈이라고 한다.)

1) L1 norm (= Manhattan distance)
L1 norm은 각 차원에 해당하는 값의 절댓값을 다 더해주면 된다. 따라서, A,B의 L1 norm은 각각 2, 7이 된다. 공식에서 k는 벡터의 차원 수를 뜻한다. 즉, 모든 차원에 대해서 계산하라는 뜻이다.
2) L2 norm(=Euclidean distance)
L2 norm은 우리가 흔히 얘기하는 원점으로부터의 거리이다. 원래 계산하던대로 하면 된다.
3) Max norm ( Infinity Norm)
Max norm은 각 차원의 원소들의 절댓값 중 가장 큰 값을 고르면 된다. 위의 사진의 공식에는 절댓값을 쓰는 것을 까먹었지만, 절댓값을 꼭 취해줘야 한다.
지금까지 나온 식들을 보면 일반화가 가능해보인다. 일반화를 통해 n차 norm, 혹은 Ln norm을 정의하면 위의 사진의 공식이 나오게 된다. L1, L2 공식을 기억할 필요 없이 일반화된 공식만 기억하면 된다.
이제 norm의 개념은 얼추 정리한 것 같다. 그렇다면 위의 사진에 L1, L2 distance 밑에 있는 그래프 2개는 무엇을 뜻할까? 찾아보니 그냥 각 차원에서 norm 값이 1이 되는 모든 벡터들을 그린 것이라고 한다. 벡터 x=(x1,x2) 가 있다고 하자. 가로축과 세로축을 각각 x1, x2에 해당하는 축이라고 생각하면, 위의 그림을 얻을 수 있다. 더 자세히 살펴보자.
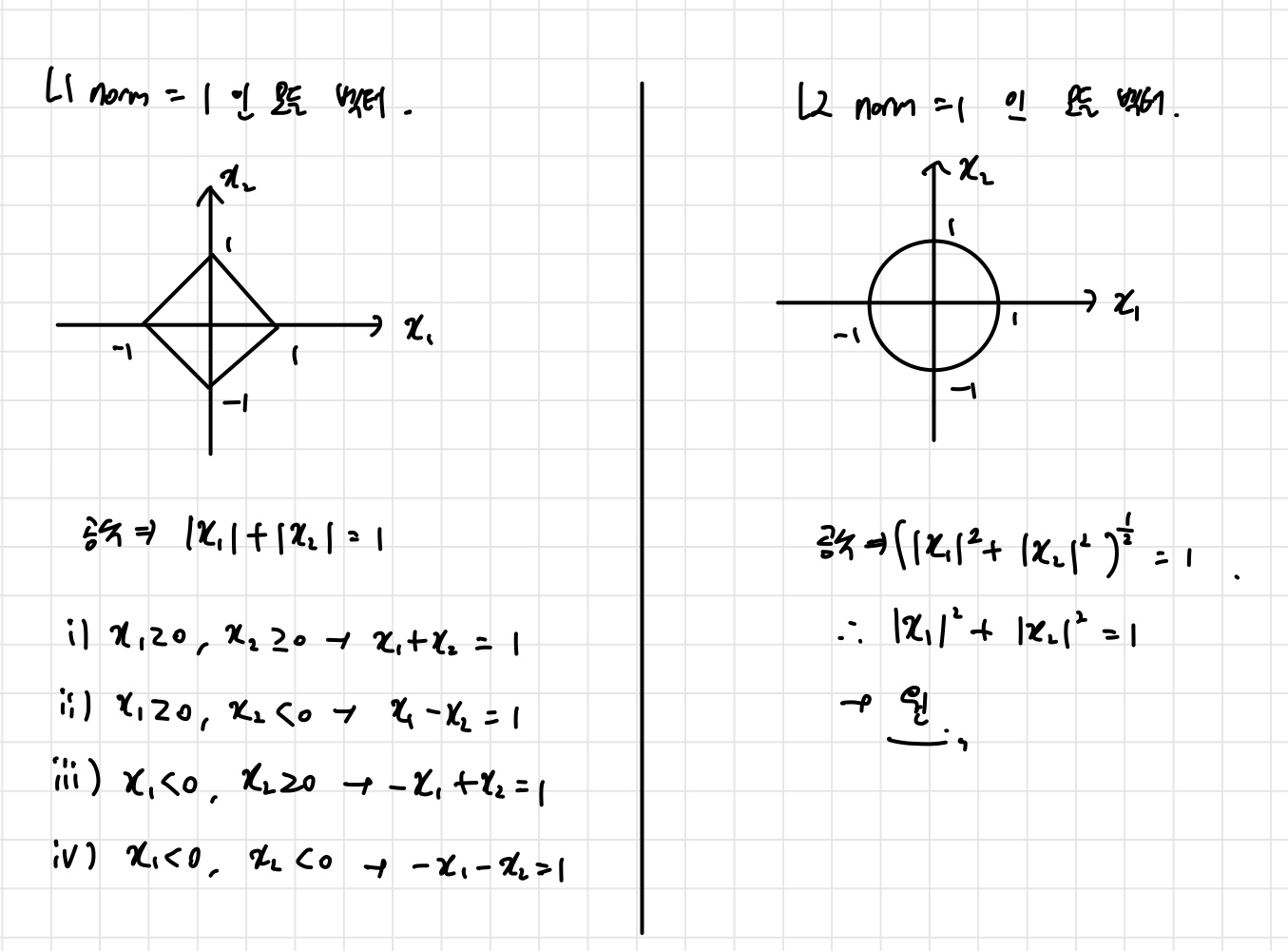
L1 norm=1이 되는 모든 벡터를 그리려면 범위를 분리해서 생각해야 한다. 인 경우부터, 인 경우까지 4가지 경우로 나누어서 생각해야한다는 뜻이다. 이를 하나의 그림에 나타내면 정사각형을 돌린 형태가 나타나게 되는 것이다. 마찬가지로 L2 norm=1이 되는 모든 벡터를 그리면, 원의 형태가 된다는 것을 알 수 있다.
그렇다면 L1과 L2 metric은 무슨 차이가 있을까? 좌표축을 회전시킨다고 생각해보자. 그래프에서도 나타나듯이, L1 distance는 좌표축이 회전함에 따라 변하게 될 것이다. 그러나 L2 distance의 경우, 그래프가 원이기 때문에 좌표축 회전의 영향을 받지 않는다. 결국 우리는 이 metric들을 데이터에 적용시키기 위해 사용할텐데, 데이터의 특성에 따라 metric을 고르는 것이 좋다고 한다. 만약 내 데이터의 각 원소들이 중요한 의미가 있다면, L1 distance를 적용하는 것이 자연스러운 선택이고, 뭐가 중요한지 잘 모르는 상태라면 L2 distance를 적용하는 것이 좋은 선택이라고 한다. 이 개념들의 장점은 distance metric을 정의해주기만 한다면 다양한 종류의 알고리즘에 적용할 수 있다는 데에 있다.
