Likelihood/ MLE

  cs231n 3강을 복습하며 정리할 마지막 글이다. 정확히 아는게 없어서 현타가 온다...ㅋㅋㅋㅋㅋ 하여튼 이번에 정리할 개념은 우도. 최대우도법이다. 영어로는 Likelihood, MLE(Maximum Likelihood Estimation)이다. 가장 헷갈리고 정리하기 귀찮았던 개념인 것 같다.

1. Likelihood

  likelihood는 한글로 가능도, 우도라고 한다. 느낌상 확률과 비슷한 개념인 것 같다. 그러나 구글에 likelihood를 치면 가장 많이 나오는 것이 probability vs likelihood이다. 그래서 나도 확률과 우도의 차이점부터 살펴보고자 한다. 둘의 가장 큰 차이점은 확률 분포가 주어지냐 안 주어지냐에 있다. 확률은 이미 우리에게 확률분포가 주어지고, 우리는 이를 통해 각 사건에 대한 확률을 계산한다. 그러나 우도는 확률 분포가 주어지지 않는다. 우리에게 주어지는 것은 데이터 뿐이다.
 데이터로 뭘 어쩌라는 것인가? 하는 생각이 든다. 우리의 목적은 이 데이터를 가장 잘 설명하는 식을 찾는 것이다. 아래 예시를 통해 더 정확히 우도의 개념을 알아보자.

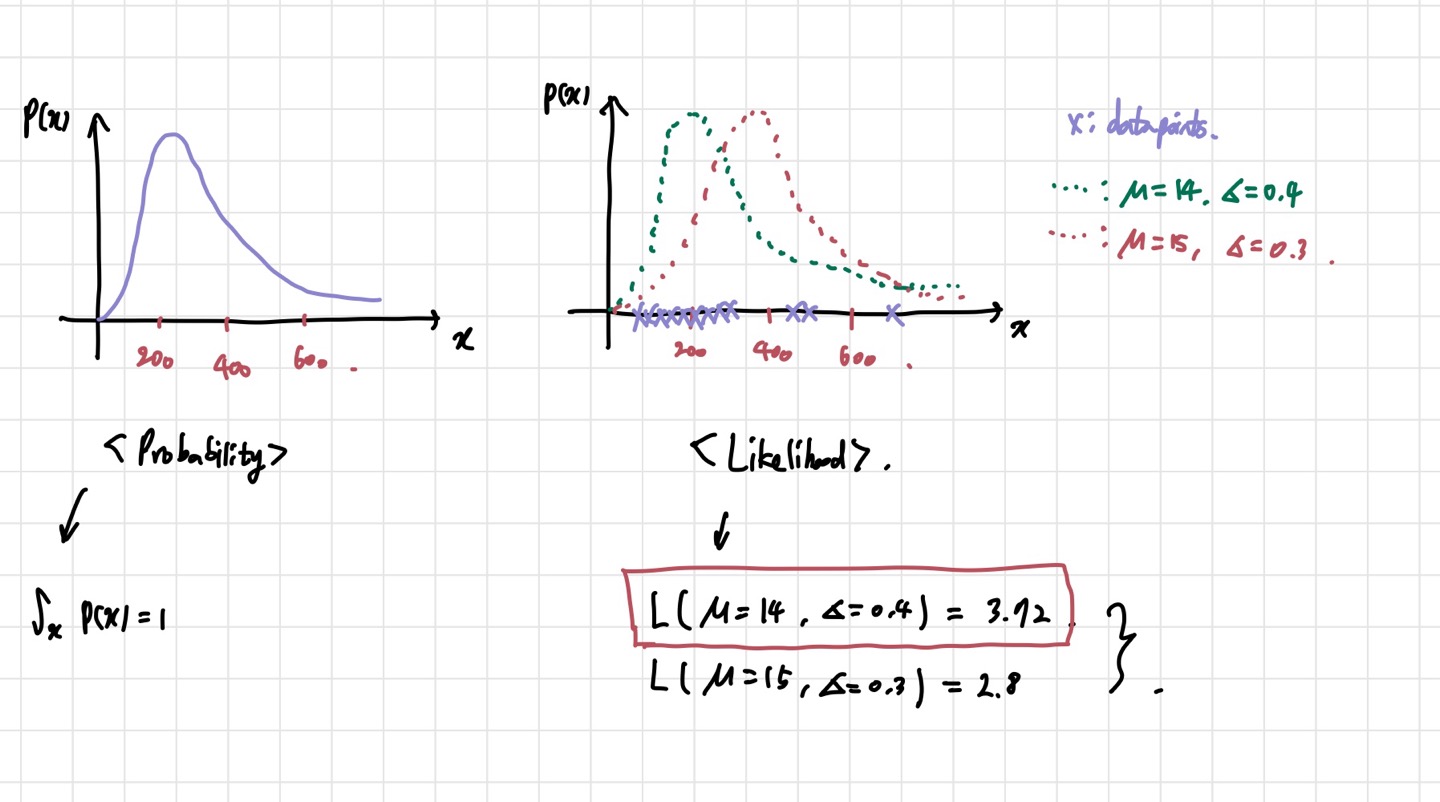
  먼저 왼쪽의 그래프는 그냥 일반적은 확률밀도함수이다. 확률밀도함수에서 전 구간의 적분값은 확률의 합인 1이다. likelihood를 계산할 때는 이런 분포가 주어지지 않는다. 오른쪽의 그래프에서 x자로 표현된 datapoint 들만 주어진다. 그러면 우리는 평균, 분산과 같은 파라미터들을 조정해서 이 datapoint들을 가장 잘 설명하는 분포를 예측하는 것이다. 위의 경우에서는 평균=14, 표준편차=0.4인 분포가 데이터를 더 잘 설명하는 것처럼 보인다.
 그런데 문제가 있다. 예측한 분포가 얼마나 좋은지 수학적으로 표현할 수 있는 방법이 있어야 한다. 즉, Likelihood function을 정의해야 한다는 뜻이다.

2. MLE

  Likelihood function을 정의하기 전에 MLE가 무엇인지부터 살펴보자. 여러 파라미터($\theta$)들로 구성된 $P(x|\theta)$에서 관측된 data $x$가 있다고 해보자. 물론, $P(x|\theta)$는 우리가 모르는 분포이다. $\theta$들을 통해 추정하는 것이다. 정리하자면, MLE는 data $x$를 이용해 $P(x|\theta)$를 추정하는 방법인 것이다.

  위의 사진과 같이 Likelihood function을 정의했다. log-likelihood function을 굳이 정의하는 이유는 그냥 덧셈으로 계산하면 편하기 때문이다.
 내가 여기서 궁금했던 점은 $L(\theta|x)$과 $P(x|\theta)$의 차이이다. 왜 $x$와 $\theta$의 위치가 갑자기 바뀌는지 이해가 되지 않았다. 이건 그냥 관점의 차이였다. 무엇에 대한 함수로 보고싶은지에 대한 표현인 것이다. 실제로 likelihood function을 계산하려면 $\theta$들을 통해 얻은 분포를 이용해야 한다. 그렇기 때문에 $P(x|\theta)$는 예측한 $\theta$를 바탕으로 얻은 분포를 의미하고, $L(\theta|x)$는 데이터를 통해 얻은 $\theta$ 라고 생각하면 될 것이다. 말 그대로 관점의 차이인 것이다. $L(\theta|x)$는 likelihood function을 $\theta$에 대한 함수로 생각하고 싶다는 의도 정도로 해석하면 될 것 같다.
 이렇게 정의한 Likelihood function을 이용해 최적의 분포을 추정하자. 간단히 얘기하면, $L(\theta|x)$를 최대화하는 $\theta$들을 구하면 되는 것이다.
 이 개념은 이 정도로 정리하겠다. 더 자세히 알아볼 기회가 있다면 하겠지만, 일단 이 정도로 정리하면 cs231n 3강을 이해하는데 큰 문제는 없어보인다.

3. 참고

  이번 글도 저번 글과 마찬가지로 '공돌이의 수학정리노트' 님의 영상/블로그를 참고했다. 정리해놓으신 게 워낙 많아서 공부할 때 많은 도움이 된다.
https://www.youtube.com/watch?v=XhlfVtGb19c&t=444s

이 외국인 유튜버 분도 많은 도움이 됐다.
https://www.youtube.com/watch?v=-eGJuwQ5A2o&t=1432s