이번 글은 PCA(주성분 분석)을 다뤄보려고 한다. 선형대수에 나오는 개념이라고 하는데, 우리 학교 수업에서는 다루지 않아 아주 안타깝다. 인공지능 공부를 하다보면 많이 쓰인다고 하진 않지만, 머신러닝 쪽에서는 많이 쓰이는 것 같아 정리할 필요성을 느꼈다.
PCA의 가장 큰 목적은 차원 축소이다. 3,4 차원 혹은 그 이상의 차원들에서는 데이터를 직관적으로 보기 힘들다. 그렇기 때문에 데이터의 중요한 부분들을 긁어 모아서 보기 편하게 바꿔보겠다는 것이다. 여기서 보기 편하려면 당연히, 고차원의 데이터를 우리가 보기 편한 2차원정도로 축소하는 과정이 필요하다. 예시를 통해 알아보자.
1. 2차원 데이터
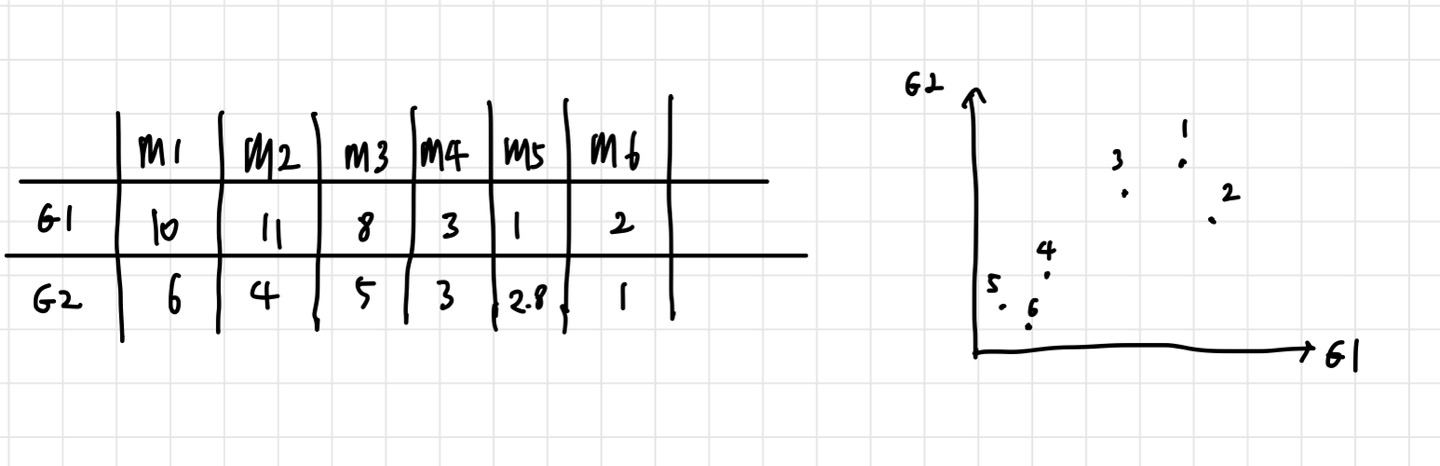
위와 같이 2차원 데이터를 가지고 PCA를 진행해보자. 실제로는 데이터가 더 고차원이지만, PCA를 이해하기에는 2차원이 적합하다. 위의 사진은 데이터를 나타내는 표와, 그 데이터를 좌표평면에 그린 결과이다. 우리는 이 데이터를 가장 잘 표현하는 선을 찾고 싶은 것이다. 데이터를 가장 잘 표현하는 선을 구해야 어떤 데이터가 실제로 더 중요한지에 대한 감이 올 것이기 때문이다. 그러나 선을 찾기 전에 해야 할 것들이 있다. 데이터의 중심을 찾고, zero centered data로 만들어야 한다. 데이터의 중심은 각 차원의 평균을 찾으면 된다.
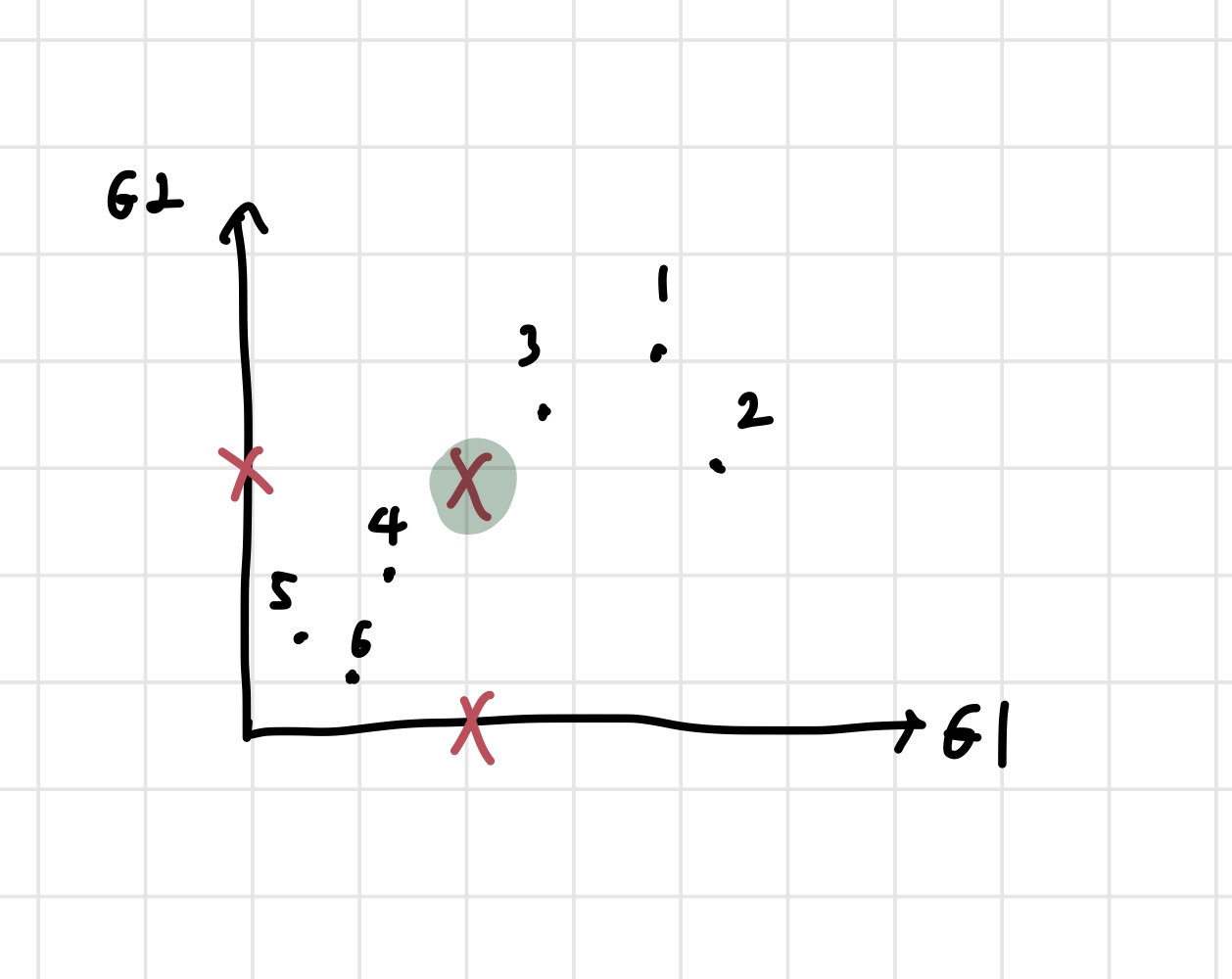
각 축의 x 표시는 축의 평균을 나타낸다. 각 축의 평균을 좌표삼아 데이터의 중심을 찾을 수 있다. 초록색으로 형광펜을 칠한 부분이 데이터의 중심이 되는 것이다. 이제 중심을 찾았으니, zero centered data로 만들어준다. 그냥 초록색 점이 원점이 되도록 평행이동 시킨다고 생각하면 된다.
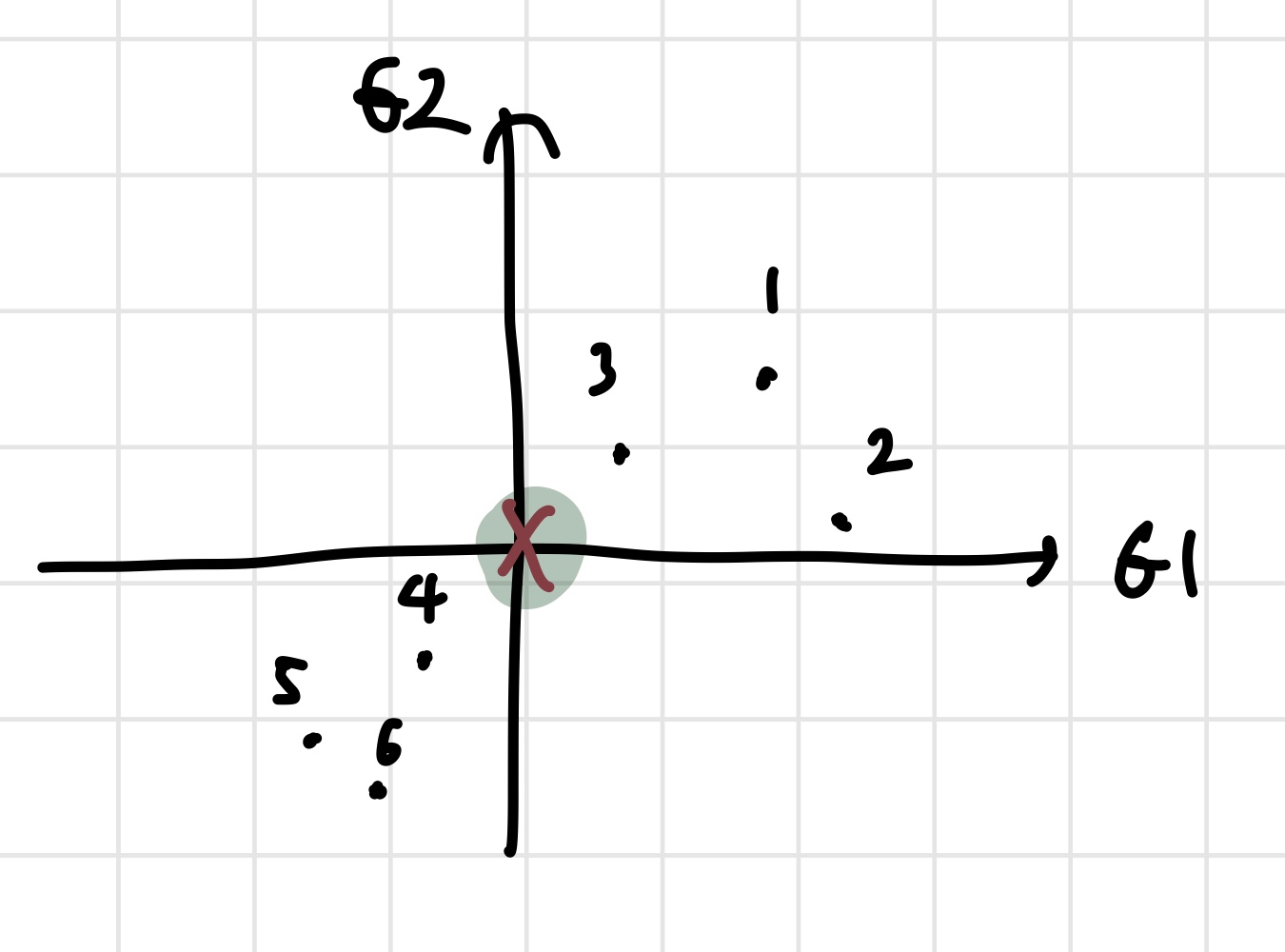
이렇게 zero centered data를 만들었다. 이제 이 데이터를 가장 잘 설명하고, 원점을 지나는 직선을 찾아보자. 그런데 그 전에 짚고 넘어가야 할 부분이 있다. PCA가 데이터를 가장 잘 설명하는 선을 어떻게 판별할 것인지에 대한 기준이 없다. 이것에 대해 2가지 기준을 생각해볼 수 있다.
1) 직관적으로, 데이터로부터 선까지의 거리의 합을 최소화 시킨다.
2) 선으로 사영된 데이터들의 점과 원점간의 거리를 최대화 시킨다.
이렇게 두 가지 방법이 있다. 결론적으로, 1번과 2번은 같은 이야기이다. 그러나 직관적으로 이해가 되는 1번에 비해 2번은 왜 최적의 선을 찾는데 도움을 주는지 헷갈린다.
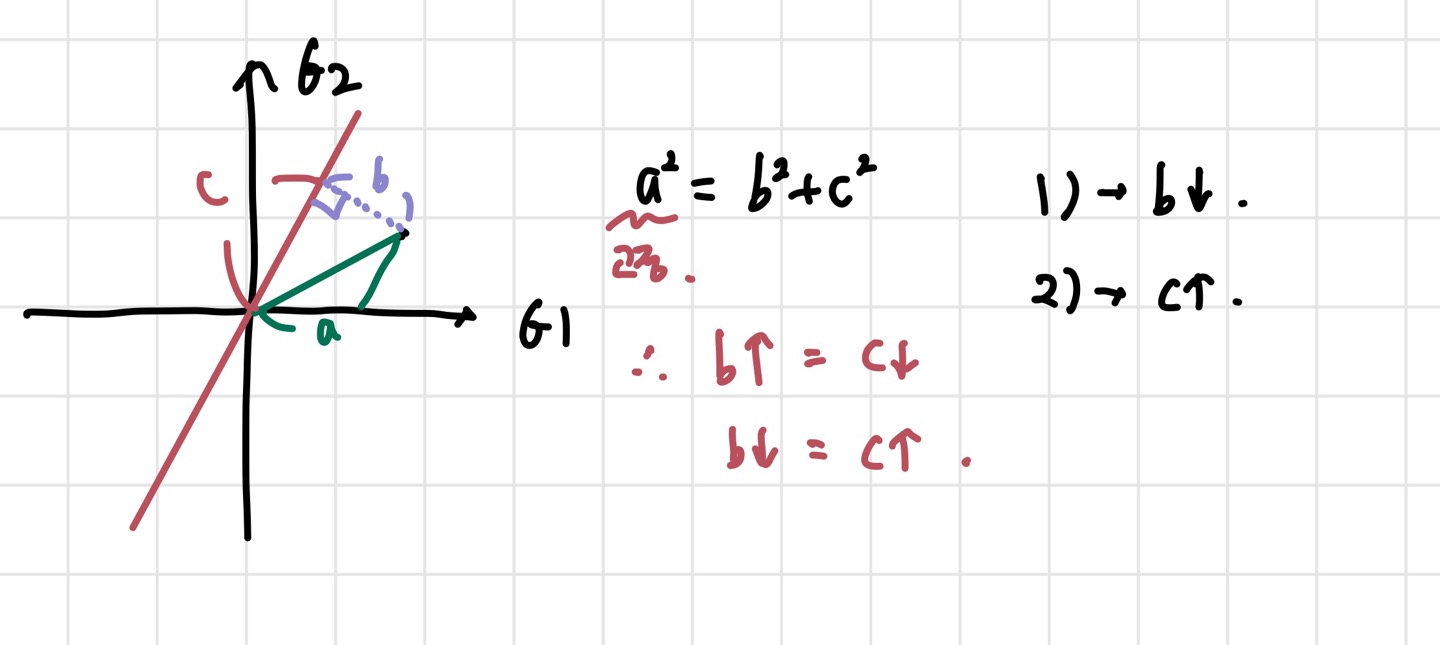
이해를 위해 하나의 data point와 우리가 최적화하려고 하는 선이 있다고 해보자. 피타고라스 정리를 통해 쉽게 이해할 수 있다. 위의 그림에서 피타고라스 정리를 적용해보자. 이때, a는 원점으로부터 데이터까지의 거리이므로 변하지 않는다. 만약 선이 최적화를 위해 움직인다면, 변하는 것은 b,c 값일 것이다. 그런데 a가 고정이므로, b가 커지면 c는 작아지고, 그 반대도 마찬가지이다. 그렇다면, 우리가 앞서 언급한 기준 1),2)를 a,b,c의 문자들로 표현해보자. 1)는 b를 최소화 시키는 것, 2)는 c를 최대화 시키는 것에 해당한다. 그러니까 사실 두 방법은 같은 방법인 것이다. c를 최대화 시키면 b를 최소화시키는 것이나 마찬가지이기 때문이다. 둘 중에 아무거나 해도 되지만, c를 최대화 하는 방법이 더 구현하기 좋다고 한다.
따라서 PCA는 모든 데이터의 c 값을 계산해서 그것들을 제곱한 후 다 더해주는 과정을 거친다. c가 최대화 되는 방향으로 이 과정을 계속 반복하면, 결과적으로 최적의 선을 찾을 수 있다. (제곱을 하는 이유는 음수값들을 없애주기 위해서이다.)
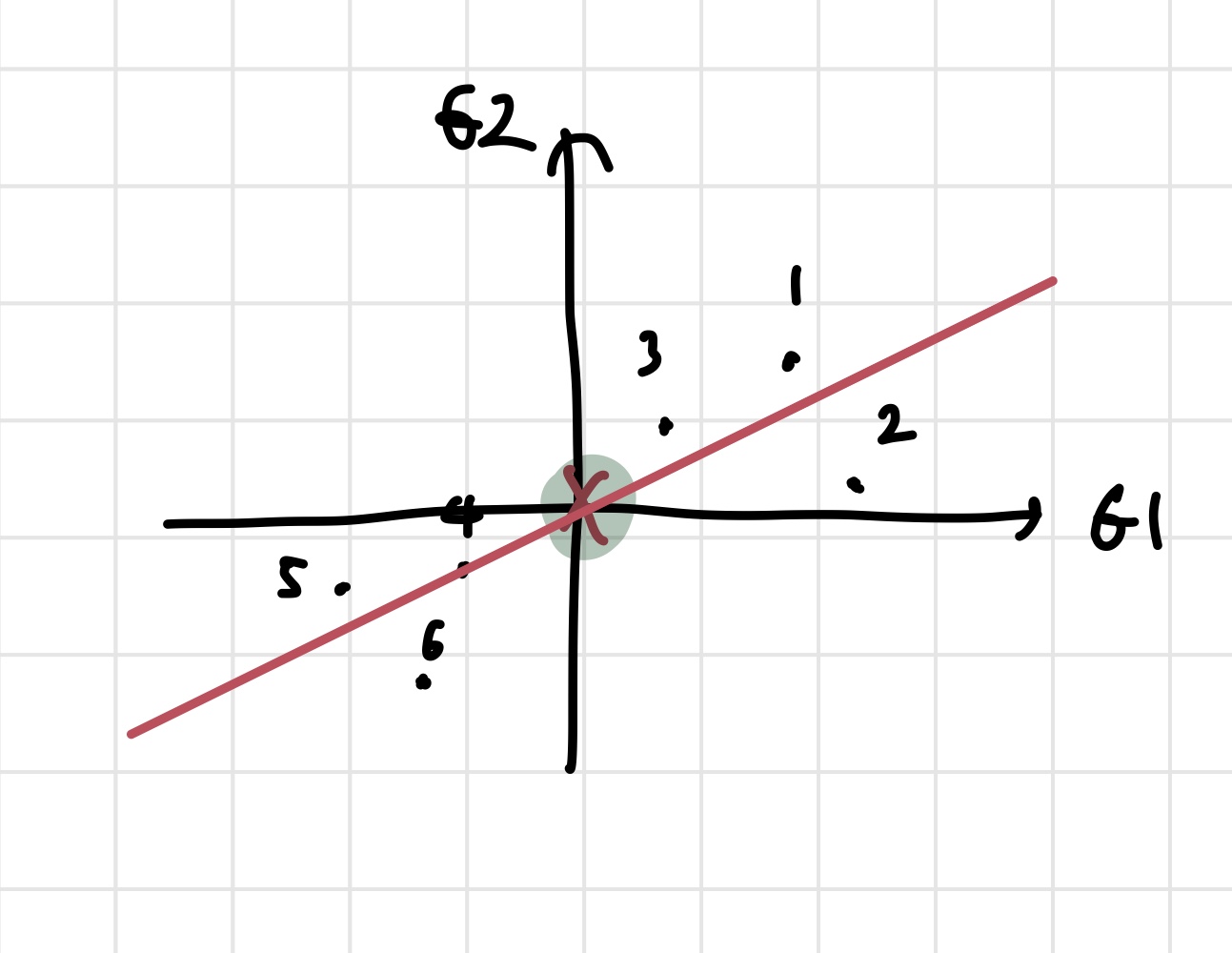
unit vector를 찾아야 하기 때문에, PC1과 같은 방향이고, 길이가 1이 되는 벡터를 찾아야 한다. 이 벡터는 PC1의 eigenvector가 된다. 참고로 loading score라는 표현이 자주 등장하는데, 이는 각 차원의 비율을 말한다. 우리가 다루고 있는 예시의 경우, G1,G2의 비율을 뜻한다. G1 0.97, G2 0.242 라고 표현할 수 있다. 또한, PC1의 eigenvalue는 거리 제곱의 평균을 계산하면 얻을 수 있다. 구체적인 식은 아래와 같이 쓸 수 있다.
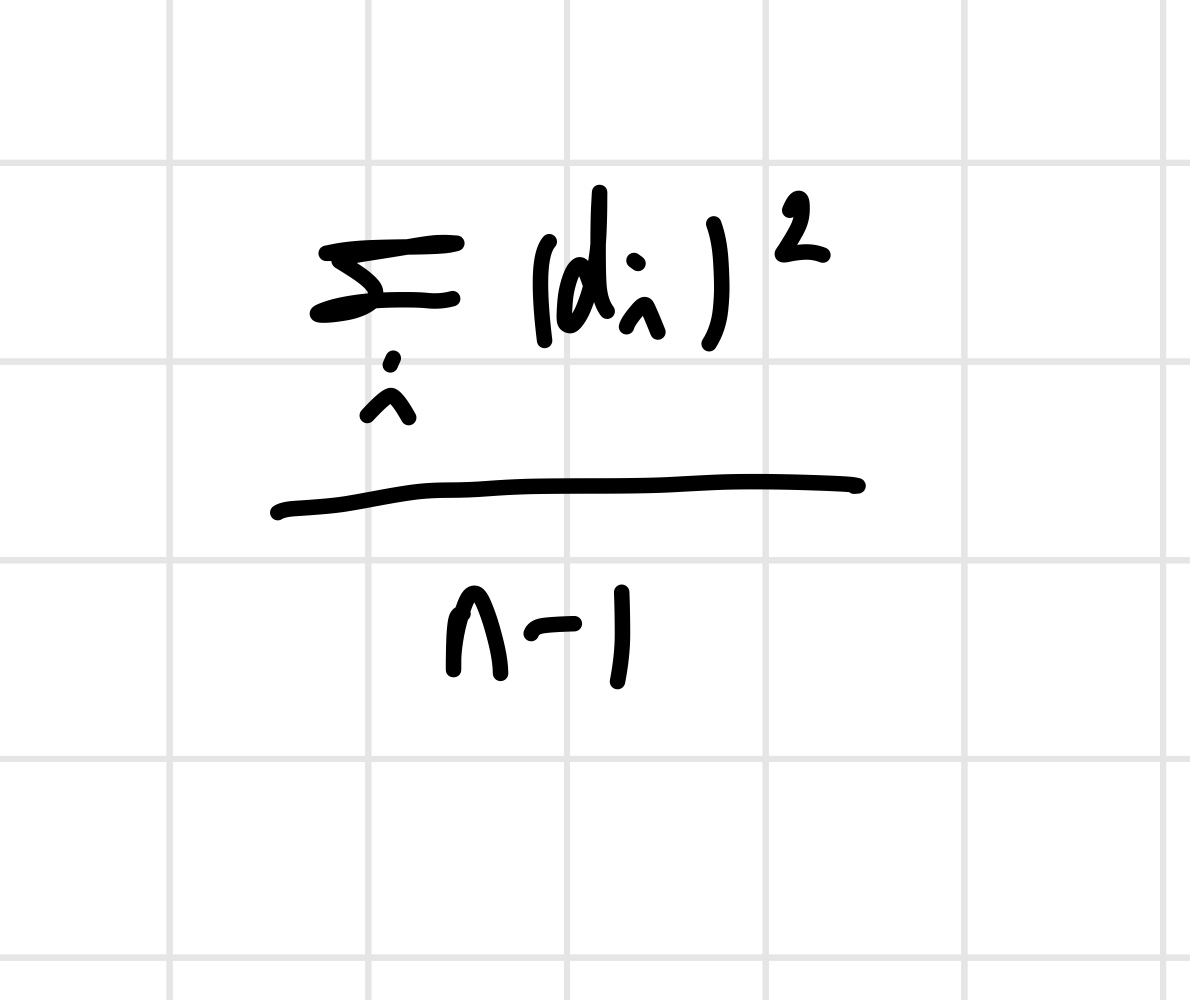
거리 제곱의 합에 루트를 씌우면 PC1의 singular value도 구할 수 있다고 한다. 이제 PC2도 구해보자. PC2는 위에서 거쳤던 과정들을 거칠 필요가 없다. PC1에 수직이고, 원점을 지나는 직선을 구하면 되기 때문이다.
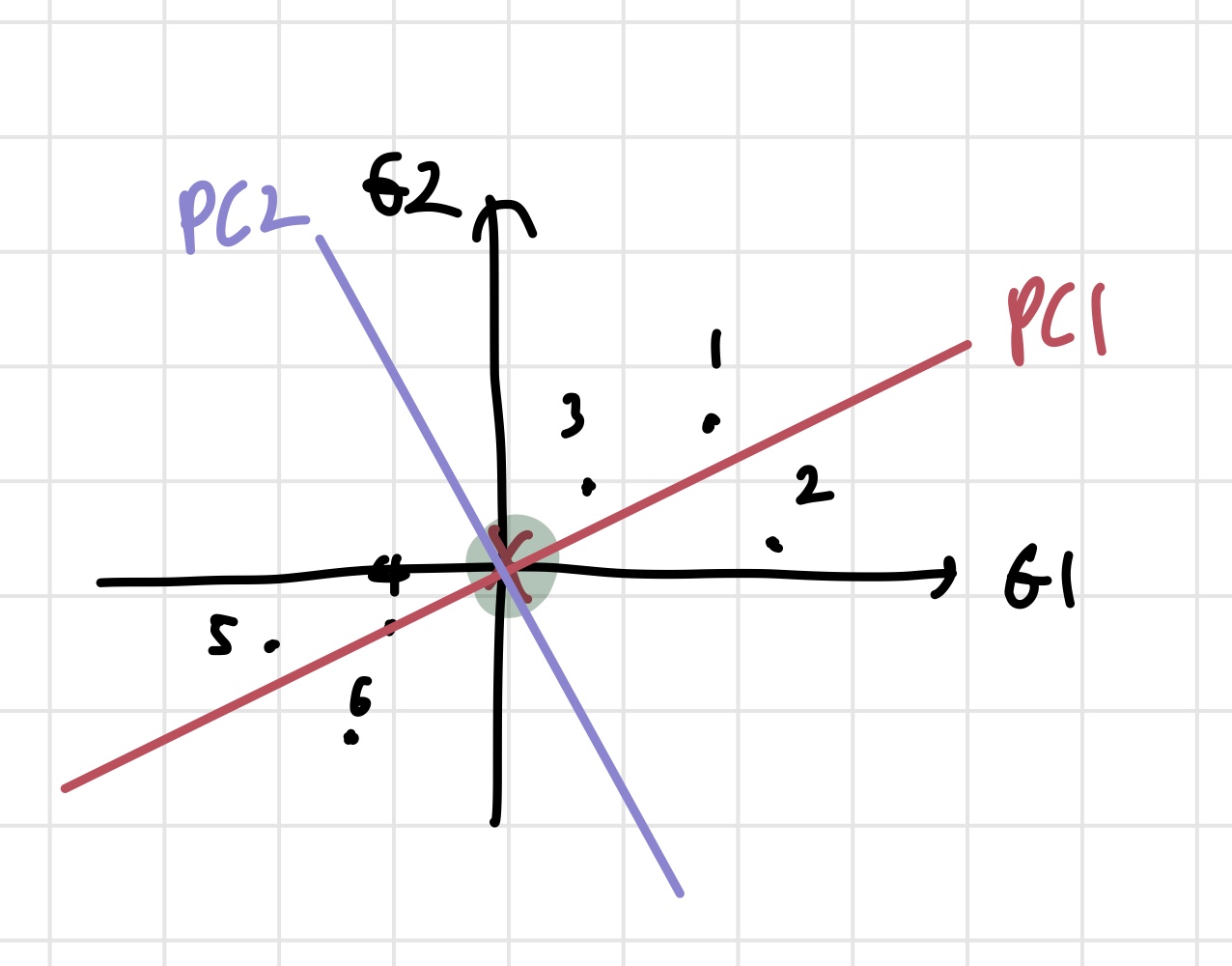
이렇게 PC2까지 구했다. PC2는 PC1과 수직이므로 기울기는 -4이다. loading score는 -0.242 of G1, 0.97 of G2라고 표현될 수 있다. eigenvector와 eigenvalue는 위에서 구한 것과 동일한 방식으로 구할 수 있다. 이제 할 일은 데이터를 PC1, PC2를 축으로 삼아 표현하는 것이다. PC1, PC2를 돌려서 좌표평면의 x,y축으로 만들자.
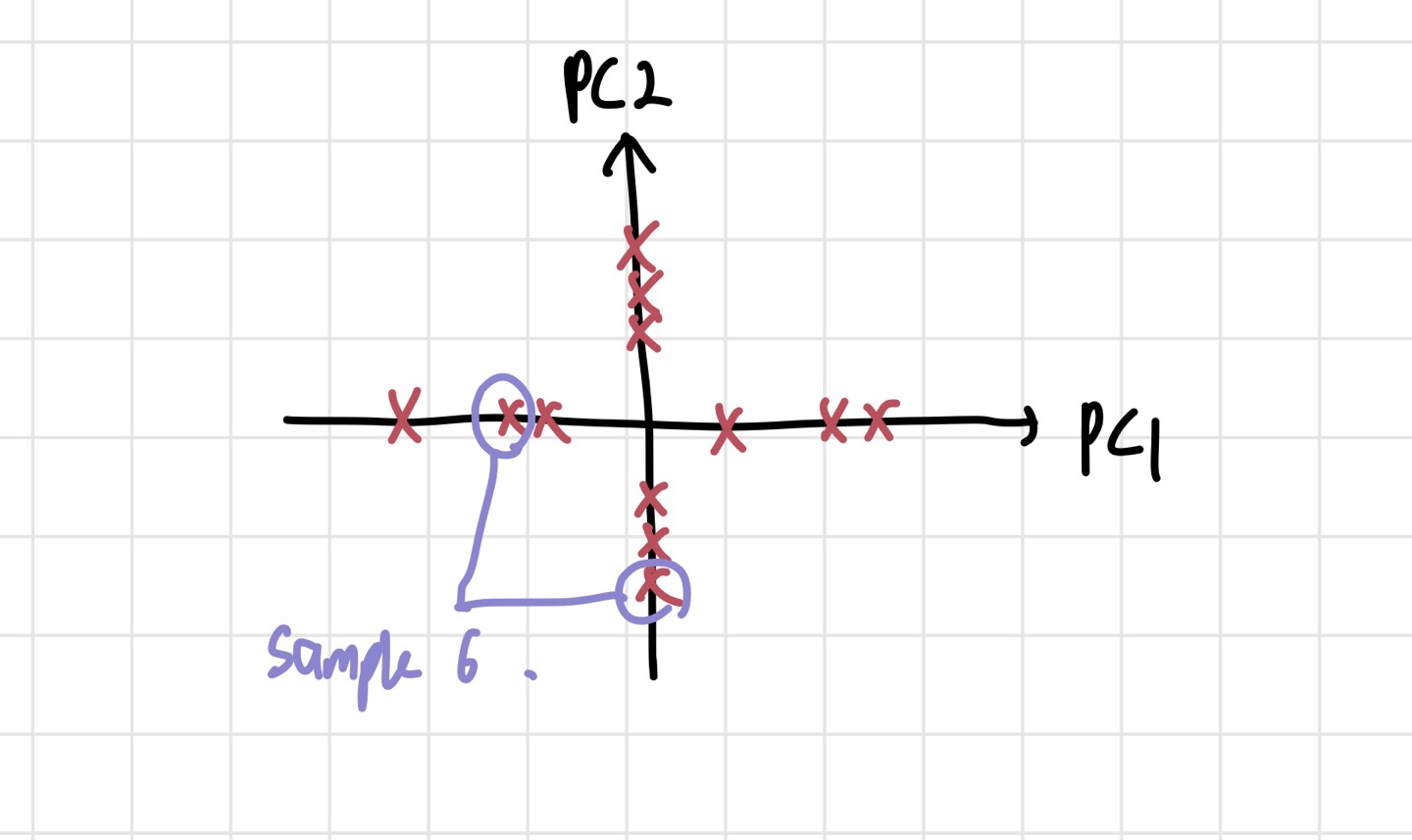
각 차원의 x 표시는 데이터들을 각 차원으로 사영한 점들을 표시한 것이다. 위의 사진에서처럼 각 차원에서 M6에 해당하는 좌표들을 모아 PC1과 PC2 축에서 어디 있는지 알 수 있다. 이제 데이터들을 PC1과 PC2에 대해 나타냈다. 그런데 둘 중에 어떤 축에 데이터에 대한 중요한 정보가 더 들어있는지 알 수 있는 방법은 없을까? 이 질문은 2차원 데이터를 다룰때는 중요해보이지 않지만, 3,4차원의 데이터에 경우 1,2개의 차원을 없애야 하기 때문에 어떤 차원을 없애야 할지에 대한 고민을 해야한다. 이 고민의 답이 되어주는 것이 분산의 개념이다. 전체 분산의 대부분의 분산을 책임지는 PC들을 선별하면, 차원을 줄여도 정확도가 그다지 떨어지지 않을 것이다.
지금까지 우리가 썼던 식 중에 분산과 가장 비슷한 식은 eigenvalue 식이다.
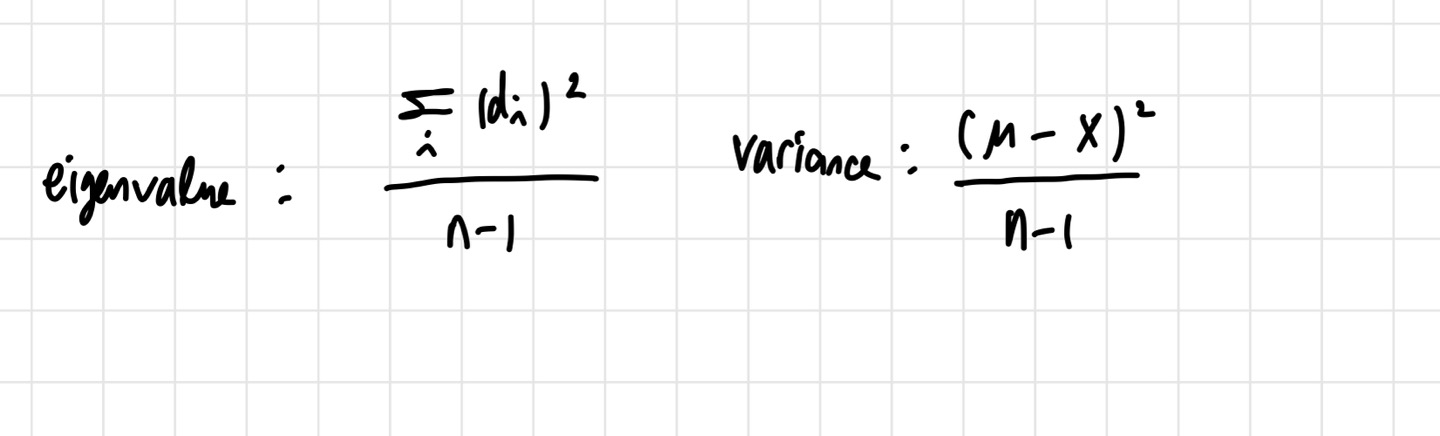
우리가 다루는 데이터는 zero mean이기 때문에 variance 식에 평균=0을 대입하면 eigenvalue 구하는 식과 같게 된다. 만약 PC1의 분산=15, PC2의 분산=3 이면, PC1은 전체 분산의 15/18=83%, PC2는 3/18=17% 를 얻는다. 이를 표로 나타낸 것이 scree plot이다. 각 PC가 얼마만큼 분산을 설명하는지에 대한 표이다.
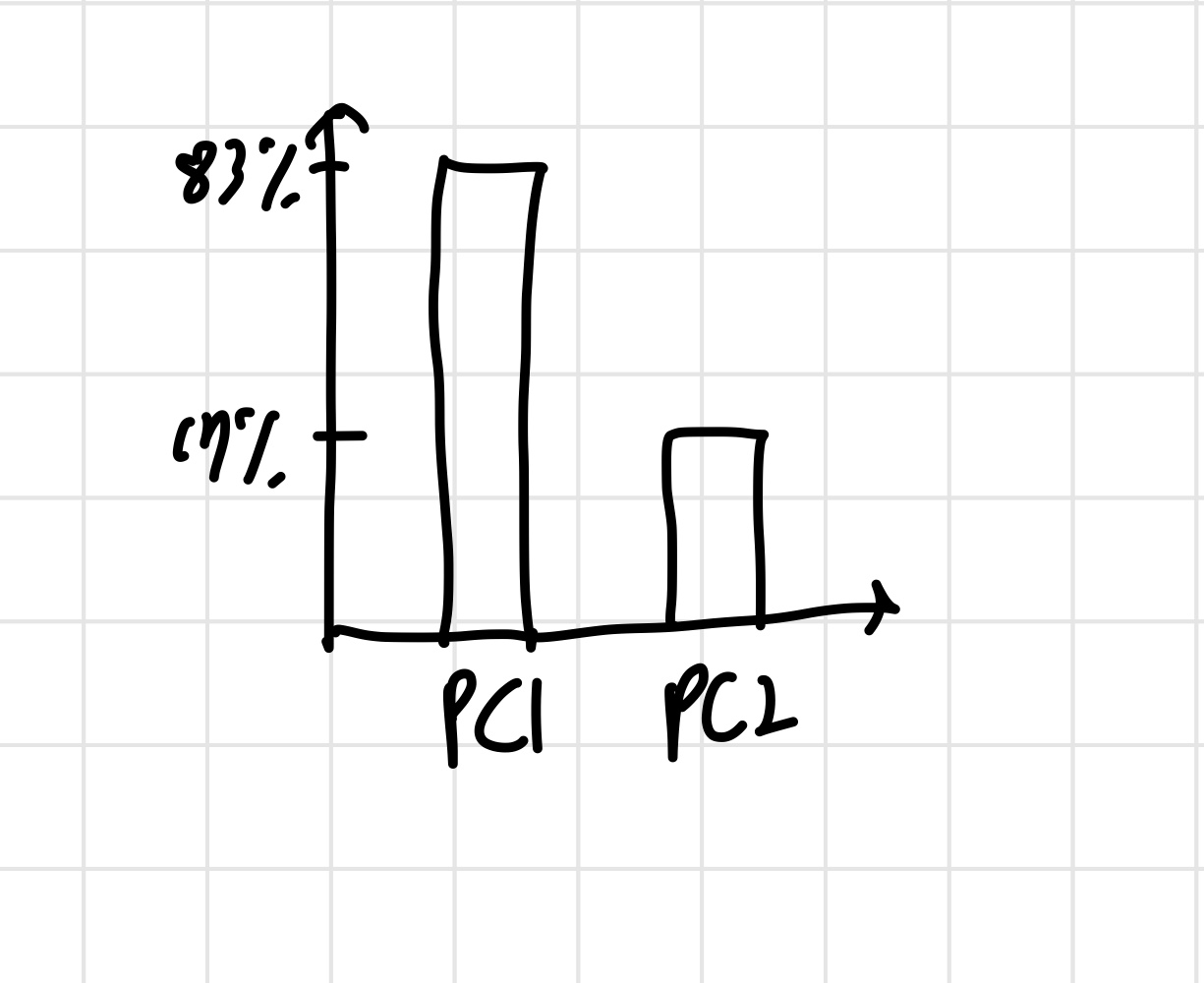
이런 식으로 나타내는 것이다. 이것이 PCA의 목적이다. 각 PC가 얼마만큼 분산을 설명하는지에 대한 정보를 얻어서, 차원을 축소하는 것이다. 이제 3차원 예시를 통해 마지막으로 정리해보자.
2. 3차원 데이터
3차원 데이터라고 해서 달라질 것은 없다. zero centered data를 만들고, PC1을 구한다. 계산 결과 loading score가
G1 0.62
G2 0.15
G3 0.77
와 같이 나왔다고 하자. G3가 PC1에서 가장 중요한 차원으로 보인다.
PC1을 구했으니 PC1에 수직이고 원점을 지나는 PC2를 구해야 한다. 그리고 나서 PC1, PC2에 모두 수직이고 원점을 지나는 PC3를 구한다.
그리고 eigenvalue 값들을 이용해 scree plot을 그린다.
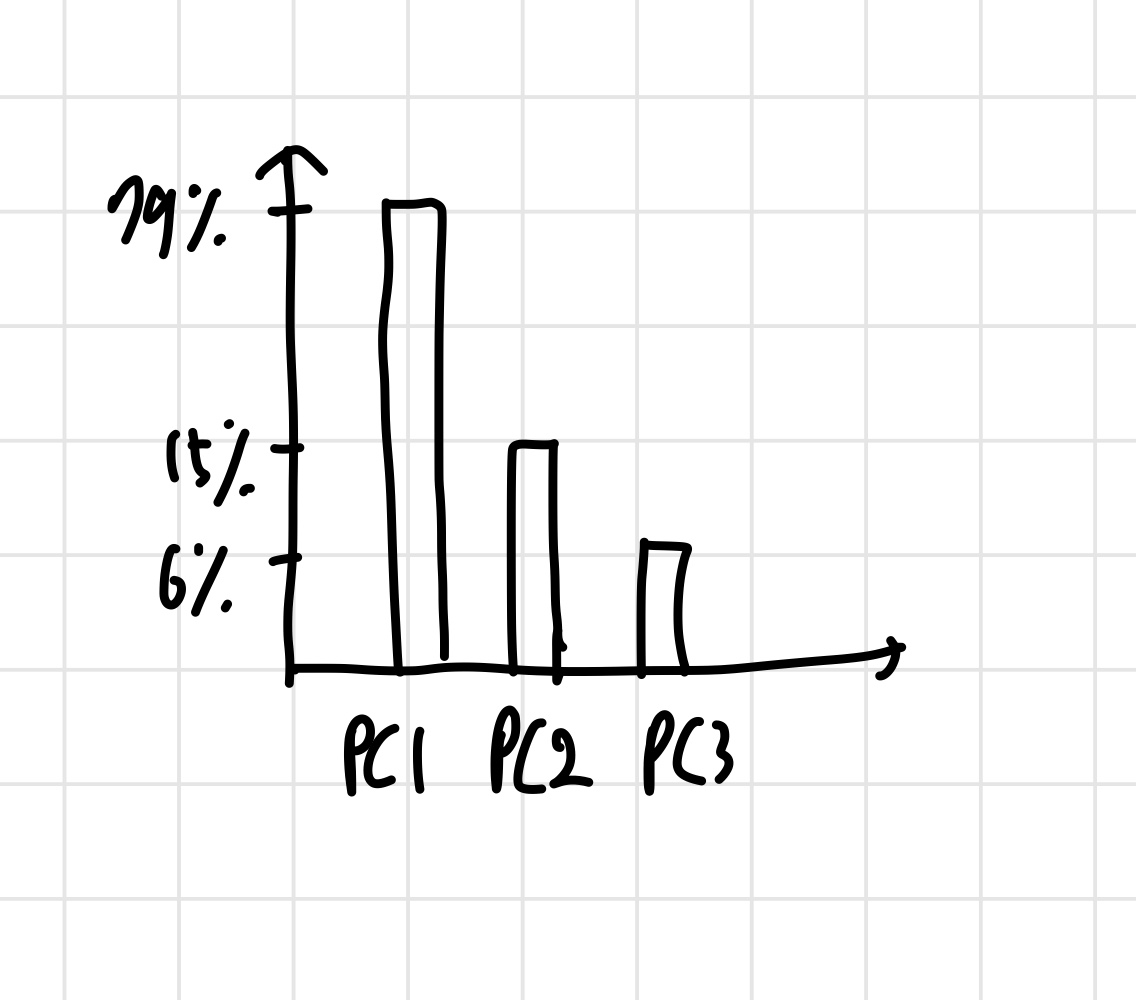
위와 같이 나왔다고 하자. 여기서 알 수 있는 것은, PC1,PC2가 전체 분산의 94%를 설명한다는 사실이다. 이렇게 되면, PC3는 없애도 된다. 그렇기 때문에, PC 축으로 이루어진 그래프에서 PC1,PC2, 데이터 좌표만 빼고 다 지우면 된다. 그리고 나서 PC1,PC2에 대해 데이터를 새로 그린다. 3차원이었던 그래프가 2차원이 되니, 조금 더 직관적으로 데이터에 대한 이해가 가능하다. 차원이 더 높아져도 변하는 것은 없다.
3. 예외
만약 scree plot을 그렸는데 모든 PC가 비슷한 정도로 분산을 나눠 갖고 있다면, 2개의 PC만 가지고 데이터를 시각화 하는 것은 별 의미가 없을 것이다. 분산의 전체적인 기조를 설명하기에 부족하기 때문이다. 데이터가 어떻게 cluster를 이루고 있는지에 대한 이해도는 높일 수 있지만, 우리가 원래 하려던 대로 차원 축소를 통해 데이터를 시각화하는 것은 정확도가 떨어질 것이다.
4. 실전에서의 팁
1) 각 차원의 scale이 비슷해야 한다.
만약 그렇지 않다면 loading score에 bias가 생길 수 있고, 분산(eigenvalue)을 계산하는데도 정확성이 떨어진다. 그렇기 때문에 대부분 각 차원의 standard deviation(표준편차)로 나눠줌으로써 bias를 방지한다.
2) 프로그램이 zero centered data를 자동으로 만들어주지 않을 수도 있다.
그렇다면 우리가 코딩을 통해 zero centerd data로 만들어주고 프로그램을 돌려야 한다.
